以游戏为载体 发展思维能力——《棋盘上的奥秘》教学设计与思考

朱姗姗

【教学内容】自编素材。

【教学过程】

一、回顾微课内容，引出课程中心

在授课前一天，学生已在家观看微课《棋盘上的奥秘》，内容为：红红和明明两人在12×12的棋盘上下棋，从右下角开始，两人轮流下，只能下在前一颗棋子的左上方距离一格或两格处，先抢到左上角的终点者获胜。红红（执白）三局都获胜。（图1）

图1　微课截图

1.回顾微课，定义必胜点。（图2）

图2

讨论“为什么红红三局都能赢？”得出“只要抢到3号点，不管对手下1格还是2格都能保证自己抢到终点”从而定义“不管对手如何下，都能保证必胜的点”为必胜点。

2.初步感受倒推，规范必胜策略的表达。

讨论“想要抢到3号点，又得下到哪些点？”得出“想要下到3号点，必须抢到2号点；想要抢到2号点，必须抢到1号点。”

小结：用倒推的方法可以找出所有的必胜点。在这个棋盘上，要后下、下必胜点，才能获胜。

【设计意图：这部分内容是整堂课的准备环节。有以下几个意图：1.在微课中演示12×12棋盘及相应游戏规则的操作，便于学生熟悉棋盘，理解8×8棋盘的游戏规则；2.引出在一维线上进行逆向推理的核心问题；3.定义了必胜点并规范必胜策略的说法，使学生后续作答更具指向性。】

二、利用8×8的棋盘，在对弈中感悟尝试和倒推

1.理解规则。

图3　师生对弈

展示题目：在8×8棋盘的右下角放一颗棋子，以它为起点，两人轮流在这个棋盘上下棋，规定只能下在前一颗棋子的上面、左面或者左上方距离一格处，先占领左上角者获胜。

（1）师生对弈两步：如果我的第一颗棋子下在这里，那么你的棋子可以下在哪里？

（2）师生对弈一局（教师执白，学生执黑），学生在“老师下到距离终点2格处点”时认输。（图3）

（3）讨论：老师下到哪个点的时候你觉得老师一定能赢，为什么？

生：老师下到距离终点两格处的点时一定赢了，因为我只能往上一格，而老师则会抢到终点。

【设计意图：因有12×12棋盘游戏的微课学习，学生对8×8棋盘上的游戏规则比较容易理解。同时加入师生对弈环节，是为了保证全班学生都能掌握游戏规则，感知必胜点，为顿悟用“倒推法”找必胜点做铺垫。】

2.探索必胜策略。

布置任务：在练习纸的对弈区，和你的同桌对弈，你下到哪个点的时候觉得自己肯定能赢，把这样的点记录在必胜点记录区。

【设计意图：在这里，我们给予学生充分的对弈体验，让学生在对弈中萌生博弈观念，初步形成倒推思路。】

3.反馈：讨论各个点是否为必胜点。

（1）错误点。（图4）

生：下到这个点，如果对手往上，我可以往左上，抢到终点；如果对手往左上，我就直接往上抢到终点。

生：（反驳）下到这个点，如果对手往左，我就只能往上，这样终点就被对手抢到，所以它不是必胜点。

小结：要考虑对方下棋的各种可能。

（2）往下、往右倒推点。（图5、图6）

生：如果我抢到这个点（图5），对手就只能往上，我就能抢到终点。

生：如果我抢到这个点（图6），对手就只能往左，我就能抢到终点。

（3）右下倒推点。（图7）

生：这个点（插小旗的点）是必胜点，如果对方往左走，那我也往左，就可以抢到1号必胜点；如果对方往上，那我也往上，就可以抢到2号必胜点；如果对方往左上，那我也往左上，就直接抢到终点。也就是说只要我抢到这个点，不管对手往哪个方向下，我都能抢到终点。（学生说完后请两位学生再把右下倒推点的验证过程说一遍）

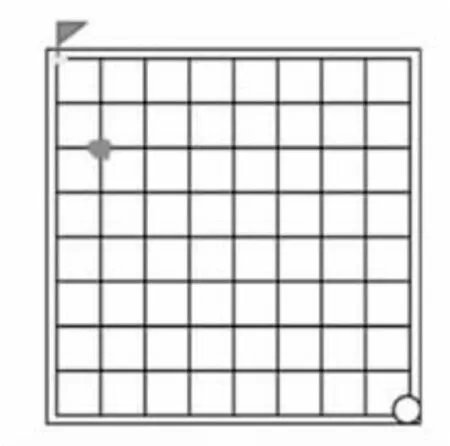
图4　错误点

图5　往下倒推点

图6　往右倒推点

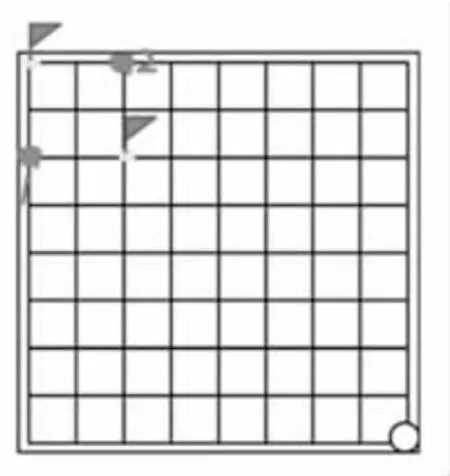
图7　右下倒推点

【设计意图：学生的对弈过程，实际上是一个尝试错误的过程。这里的反馈分为三个层次，第一个层次，反馈错误点，让学生再次明确，下棋是一种博弈，在想往对自己有利的方向发展时，对手也是这么想的，只有“不管对手如何下，都能保证必胜”的点才是必胜点；第二个层次，往右、往下的必胜点推导，为反馈右下必胜点做铺垫；第三个层次，右下必胜点推导，稍有难度，通过多次复述推理过程，让学生充分感悟推理的严密性。】

4.带领倒推。

图8

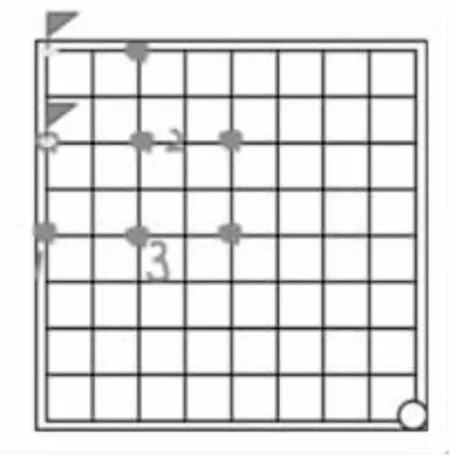
图9

（1）讨论：怎么才能抢到这个点？（图7）

①依次根据对手的各种走法说出自己的应对策略，得出必胜点。

②把这个点当成终点，沿“田”字直接倒推出这三个点。（图8）

（2）沿“田”字倒推能抢到这个点（插小旗的点）的必胜点。（图9）

【设计意图：在之前的学习中，学生已明白可以用倒推法寻找必胜点，但如何使用倒推法，仍有一定的难度。这一环节是基于学情的带领倒推，这里要反馈两种倒推方式：一是边尝试错误边倒推→对前一环节的再一次尝试和巩固；二是建立模型后的倒推→类比倒推，建立模型，学会简化。】

5.学生自主找必胜点。

【设计意图：有了前面的带领倒推，学生对全盘倒推有了一定的感知，这时候再次让学生找必胜点，能够水到渠成。】

6.师生对弈两局。（均学生赢）

学生反馈必胜策略：想要抢到这个点，必须抢到这个点；想要抢到这个点，必须抢到这个点……从终点开始往起点倒推就可以了。所以必胜策略是后走，走必胜点。（图10）

图10

【设计意图：赢了教师极大鼓舞了学生，并使学生获得了数学学习的成就感。此环节通过规范语言，经历推理过程，领悟“倒推”原理。】

7.小结：为了找到这个棋盘上的必胜策略，我们先尝试找出离终点最近的三个必胜点，再从终点开始，往起点倒推。找完必胜点之后，老师和这位同学对弈，其实就是在验证大家的必胜策略是否正确。

三、出示5×5棋盘，运用策略，巩固方法

游戏规则相同，找出5×5棋盘的必胜点，并根据必胜点确定必胜策略。

反馈：必胜点（图11）；必胜策略：先走，走必胜点。

图11

【设计意图：这一环节主要巩固倒推的方法，让学生将初步探索到的策略在变化了的情境中加以运用，在培养学生推理能力的同时锻炼其语言表述的能力。】

四、出示 8×8－5×5 棋盘，引发认知冲突

图12　学生推导必胜点

图13　师生对弈

1.同样的游戏规则，自行找出 8×8－5×5 棋盘的必胜策略。

2.反馈。（图12）

3.师生对弈验证，学生输。（图13，教师执白，学生执黑）

讨论：已找到必胜点，为什么会输？

生：没考虑老师往上走，必胜策略有误。

小结：我们用验证的方法发现必胜策略是有漏洞的，说明在倒推的过程中还需要考虑对手下棋的各种可能，让自己的思维更严谨、更全面。

【设计意图：学习了前面的知识，学生会产生思维定势，以为只要进行“田”字倒推即可，这一环节让学生产生了强烈的认知冲突，从而促进学生反思：1.得出必胜策略后要进行验证；2.倒推时务必严密。这一环节，既让学生体验了反思的重要意义，又感受到完整的解决问题的过程。】

五、回顾所学，全课小结

师：在今天这堂课上，你有什么新的收获？

生：在寻找策略的时候我们可以先尝试一下，找找感觉。

生：学会了用倒推去解决数学和生活问题。

生：思考问题要严密。

生：倒推后的顺向验证能帮我们验证倒推结果是否正确。

【课后回望】

本课例是一节数学活动课。学生在充分的活动中积累经验，教师进行适时的引导，使学生顿悟出方法的选择。在讨论中掌握方法的使用，并理解数学本质。

本课设计有以下几个特点：

一、材料创设符合学生兴趣

本课例采用学生十分喜爱的下棋游戏，学生兴趣高涨，求知欲强烈。从 8×8，5×5 到 8×8－5×5，棋盘在不断地演变，学生也在层次递进的材料引导下不断地触碰他们的“最近发展区”，从原来没有一个学生能够解决问题到最后几乎每位学生都至少能够解决8×8的棋盘，不同程度的学生都有不同层次的收获。

二、过程展开注重自主尝试

在课堂上，教师放手让学生通过不断地出错，在尝试中进行自我纠错、反思和辨正。在师生、生生之间对弈，获得充分的感知经验后，再经过教师的引导，自发地“顿悟”：可以使用倒推策略解决问题。学生对倒推法的选择有了深刻的体验。

三、引导介入尊重契合学情

尽管在获得充分感知经验后，学生已经顿悟可以用倒推法解决问题，但如何使用倒推法进行必胜策略的推导，学生仍有困难，需要教师的及时引导。教师抓准时机，在学生的讨论中适时地进行方法点拨，让学生再次对方法的使用有所顿悟。这样的流程设计，既给了学生充分自主学习的空间、又尊重学情，既开放、又扎实。

四、教学推进关注策略与能力

本课例中，每一个过程设计都有明确的设计意图，将课时整体目标细化为环节目标。尽管材料不断演变，目标细化延展，但每一个材料和过程展开都紧紧围绕博弈思想、倒推方法，并将最大的“力气”用在培养学生的推理能力上。

授课后，我们也一直在思考棋盘的材料是否有更多可挖掘和探索的地方，也得到了很多教师的建议：如将规则改成只能往上或往左走，那么必胜策略会怎样？这时候必胜策略的得出，除了可以在棋盘上倒推，还可以将8×8棋盘上的路线拉成一条能走16步的一条线段，此时棋盘就和抢数游戏完全相通了，方法和策略也在不同的材料中延伸贯通。