北斗GEO/IGSO/MEO卫星观测值精度分析及随机模型精化

刘永建,江勇

(江苏省地质测绘院,江苏 南京 211100)

0　引　言

北斗卫星导航定位系统(BDS)于2012年底正式服务于亚太地区,目前由6颗地球静止轨道卫星(GEO),5颗倾斜地球同步轨道卫星(IGSO)以及5颗中圆轨道卫星(MEO)组成。近年来,已有学者对北斗精密定位和基线解算的数学模型进行了相应的研究[1-5]。数学模型包括函数模型和随机模型,函数模型建立了观测值与坐标参数、模糊度参数以及大气延迟等估计参数之间的相互关系;随机模型则采用方差协方差来描述观测值的统计性质[6]。虽然有学者研究表明,北斗观测数据质量与GPS不相同,并且北斗GEO、IGSO、MEO三类卫星的观测值精度也互不相同[7-8],但是北斗卫星仍采用与GPS卫星相同的随机模型,不考虑北斗卫星与GPS卫星之间以及北斗三类卫星之间的观测值精度的差别。因此,有必要分析不同类型北斗卫星伪距和相位观测值的精度和随机统计特性,在分析的基础上精化北斗系统精密定位中的随机模型。

零基线单差(SD)观测值消除了电离层延迟误差、对流层延迟误差、多路径效应误差、卫星轨道误差和卫星钟误差的影响,扣除接收机钟差后(取各卫星单差残差的均值作为接收机钟差)仅含观测值噪声,可用来评估接收机的伪距和载波相位观测值的精度[9]。在卫星定位中,常用的随机模型有高度角随机模型[10-11],但高度角随机模型在应用中模型系数一般为固定值,这不符合北斗系统混合星座的实际情况。本文通过零基线单差残差分析北斗不同类型卫星的观测值精度,在统计高度角与观测值精度关系的基础上,采用最小二乘拟合的方法分别得到北斗GEO、IGSO、MEO卫星伪距和相位的高度角随机模型,建立起适用于北斗系统的定位随机模型。

1　北斗伪距和载波相位测量精度

选取MGEX观测网中零基线CUT0-CUT2连续10天的观测数据,采集时间为2016-02-01～2016-02-10(DOY:032～041),接收机类型为Trimble NetR9,采样间隔为30 s.本文采用文献[3]中的零基线单差模型方法来求解单差残差序列。图1示出了北斗GEO/IGOS/MEO和GPS卫星伪距单差残差时间序列,图2给出了北斗GEO/IGOS/MEO和GPS卫星载波相位单差残差序列。可以看出,北斗伪距单差残差基本在-0.5 ～0.5 m之间,北斗载波相位单差残差基本在-5～5 mm之间,与GPS单差残差量级相当。并且,从长时间的单差残差时间序列来看,并未出现突变的情况,因此,北斗观测数据具有较强的稳定性。

联系人: 刘永建E-mail: jiuhua_pengz@163.com

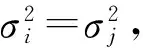
2　北斗随机模型的构建

高度角随机模型的正弦函数表达式为

(1)

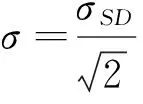
(2)

图4和图5分别为IGSO、MEO卫星伪距和相位高度角随机模型拟合曲线图,表1和表2分别给出了对应随机模型系数的拟合值,可以看出,经验值高度角随机模型与实际相差较大,因此,本文依据北斗不同类型卫星伪距和相位观测精度建立精化随机模型是有必要的。由于GEO卫星高度角变化很小,并且在第一节得出了GEO卫星观测值精度略小于IGSO卫星,但两者非常接近,因此GEO卫星高度角随机模型的系数采用IGSO卫星的系数。

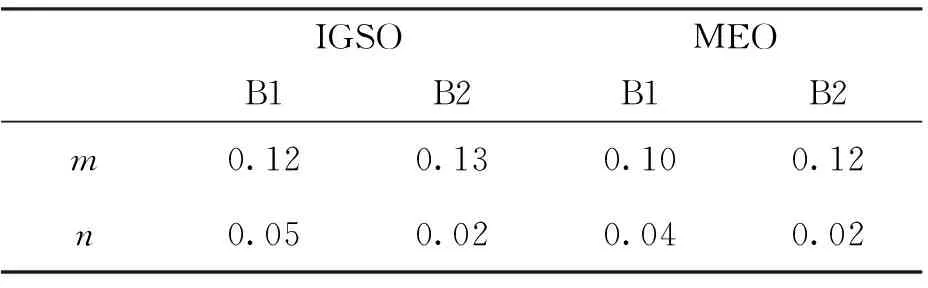
表1　伪距随机模型系数拟合值　　单位：m

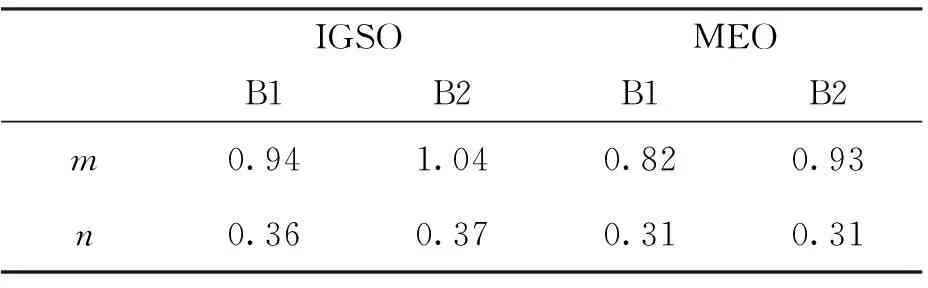
表2　相位随机模型系数拟合值　　　单位：m

3　试验分析

为了验证精化后的随机模型的性能,对静态观测基线进行单历元定位测试。测试数据来源于基线ST01-ST02,长度为6 101.4 m,采样间隔为10 s,截至高度角为10°.单历元解分别采用经验随机模型和精化后的随机模型。另外,采用长时间静态基线解算的坐标结果作为真值。

图6为精化随机模型与经验随机模型单历元定位结果比较图,给出了基线分量N、E、U方向的偏差值DN、DE、DU(单历元基线分量结果减去真值),红色的为精化随机模型结果,黑色为经验随机模型结果。表3为精化随机模型与经验随机模型单历元定位结果统计表。可以看出,精化随机模型的定位结果的偏差值总体更加平缓,从表3的统计结果计算得出,平均点位精度提高了42.1%,N、E、U方向各分量RMS改善的百分比分别为:31.6%、15.3%、31.4%.

表3　单历元定位结果的平均偏差及均方根误差RMS

4　结束语

本文对北斗观测值的噪声特性进行分析,结果表明北斗卫星伪距观测值精度要稍优于GPS,相位观测值精度与GPS相当。通过单差残差统计结果拟合出了北斗三类不同卫星伪距和相位高度角随机模型的系数,精化了随机模型,从而获得了适合北斗系统精密定位的随机模型。同时,将精化后的随机模型进行测试,结果表明提高了单历元动态定位的精度,平均点位精度提高了42.1%,N、E、U方向各分量RMS改善的百分比分别为:31.6%、15.3%、31.4%.下一步将针对不同地区数据,不同定位模式更深一步地讨论精化随机模型的适用情况。

[1]陈健,岳东杰,赵兴旺.BDS/GPS组合中长基线解算性能分析[J].全球定位系统,2016,41(6):85-91.

[2]ZHOU S S, HU X G,RUI G,etal. Positioning accuracy assessment for the 4GEO/5IGSO/2MEO Constellaton of Compass[J]. Science China Physics Mechanics &Asronomy, 2012, 55(12):2290-2299.

[3]DENG C, TANG W, LIU J,etal. Reliable single-epoch ambiguity resolution for short baselines using combined GPS/BeiDou system[J]. GPS Solutions, 2014, 18(3):375-386.

[4]HE H, LI J, YANG Y,etal. Performance assessment of single-and dual-frequency BeiDou/GPS single-epoch kinematic positioning[J]. GPS Solutions, 2014, 18(3):393-403.

[5]TEUNISSEN P J G, ODOLINSKI R, ODIJK D. Instantaneous BeiDou+GPS RTK positioning with high Cut-off elevation angles[J]. Journal of Geodesy, 2014, 88(4):335-350.

[6]张小红,丁乐乐.北斗二代观测值质量分析及随机模型精化[J].武汉大学学报(信息科学版),2013,38(7):832-835.

[7]严丽,李萌,梅熙,等.实时估计不同类型北斗卫星观测值的随机模型[J].武汉大学学报(信息科学版),2017,42(2):263-269.

[8]杨元喜,李金龙,王爱兵,等.北斗区域卫星导航系统基本导航定位性能初步评估[J].中国科学:地球科学,2014,44(1):72-81.

[9]VAZQUEZ G E. Analysis of the stochastic of GPS observables[R]. The Ohio State University Report, Ohio, 2008.

[10]戴吾蛟,丁晓利,朱建军. 基于观测值质量指标的GPS观测量随机模型分析[J].武汉大学学报(信息科学版),2008,33(7):718-722.

[11]TEVK M. The stochastic modeling of GPS observations[J]. Turkish Journal of Engineering & Environmental Sciences, 2004, 28(4):223-231.