基于岩体三维裂隙网络模型的随机块体稳定分析

李明超，张 野，周四宝



基于岩体三维裂隙网络模型的随机块体稳定分析

李明超1，张 野1，周四宝2

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300354；2. 浙江省水利水电勘测设计院，杭州 310002)

利用蒙特卡洛模拟方法和三维地质建模技术建立多边形离散裂隙网络与工程岩体的耦合模型，并对随机块体进行了识别分析，提出了一种新的随机岩石块体支护分析方法．根据空间坐标和地质属性对耦合模型进行分区，统计各个区域内块体的埋深、体积和密集度，研究随机块体的空间分布规律；在自重和地震两种情况下分别计算各区域的块体失稳概率和支护强度．通过以上参数的计算和分析，为锚杆间距、长度和锚杆支护力提供参数化指导，同时也可对支护方案进行检验．最后将该方法应用于某取水隧洞岩体支护分析中．

岩体结构；三维地质模型；多边形离散裂隙网络；随机块体；稳定性分析；块体支护

岩体中的块体分析与失稳判别对于保证工程安全十分重要．由于地层应力、地下水和温度等复杂地质过程，大规模的地质结构面(如断层、岩脉)和较小规模的地质结构面(如裂隙)均存在于岩体中．这就使得岩体具有不连续、各向异性、非均匀性的特点．大规模的地质结构较为明显，通过地质勘察可以比较准确地估计其走向、倾向和倾角等地质信息；而裂隙在浅埋深地质条件下普遍存在，对于其几何特性和力学特性，包括位置、间距、尺寸和黏聚力、内摩擦角等，在野外地质调查过程中很难得到．通常是用抽样的方法对优势组数目进行统计，得到其分布规律，从而推求结构面代数几何信息和地质信息的分布情况，建立离散裂隙网络模型；通过耦合三维离散裂隙网络模型和工程地质模型，利用布尔运算，使得大规模结构面、较小规模结构面及工程中的开挖面互相切割，生成随机块体．由于块体的位置信息、几何信息和地质信息是随机的、不确定的，所以分析较小规模的地质结构面的稳定性十分困难．

块体理论最早由Goodman和Shi[1]提出，从块体的代数几何表示、块体运动、节理块体分析等多个方面系统论述了块体理论在地面工程、地下工程和隧道工程中的应用；而国内外学者更关注裂隙结构面的几何信息模型的构建．Zheng等[2]采用Baecher圆盘模型，验证迹线服从的分布规律；Elmouttie和Poropat[3]基于蒙特卡洛模拟方法建立了更接近实际形状的裂隙模型；Sturzenegger等[4]利用陆地遥感技术对平均迹长、平均迹线密度和块体大小进行了分析，并通过参数设计对整个过程进行了优化；在Hekmatnejad 等[5]建立的模型中，不需对迹线长度和直径长度的分布进行选取即可建立模型；Han等[6]针对小样本数据，通过统计分析建立了准确度较高的离散裂隙网络模型．准确模拟离散裂隙网络可有效提高目标块体的识别，对于块体的稳定性分析有积极意义．如何使离散裂隙网络模型更接近实际成为学者们研究的重点．岳攀等[7]应用拉丁超立方抽样方法，使得最终模型的空间填充性更好，模拟效果更接近真实值；张奇等[8]基于凝聚层次聚类分析法，对裂隙长度进行自动聚类，不需提前设置聚类中心，减小主观影响；Zhan等[9]用逐步分析的方法建立了适用于力学连通率分析的离散裂隙网络模型，这种方法对于裂隙相交和连通分析十分有效；Guo等[10]提出数字技术在数据分析中的应用可以克服传统方法中样本的尺寸效应，建立更有效的模型．在随机块体生成的建模过程中，学者们总结了建模的一般方法和主要流程，使得建模过程更加智能化，通过关键参数即可控制模型的生成．dfnWorks用于研究离散裂隙网络建模，并对水在裂隙中的流动进行了模拟[11]；FracSim3D基于蒙特卡洛模拟自动生成结构面位置，并设计了统计工具对生成的结构面进行分析[12]；dfnWorks多应用于渗流的研究[13-14]，而FracSim3D则用于岩体稳定分析的研究中[15]．无论在模型参数统计分析方面[16]，还是在三维建模方面[17-18]，学者们对于块体对于岩体稳定影响的研究都已日趋成熟，但准确识别失稳块体和关键块体对科研人员依然是一个挑战，相应地也无法为隧洞支护提供参数设计指导．目前，对于随机块体地支护参数选择主要依靠经验，受主观影响因素大；同时块体稳定的分析只是利用统计的方法进行计算，在具体工程中，关键块体的识别效率并不高．

本文建立了多边形三维离散裂隙网络模型，通过对三维裂隙网络模型和工程地质模型进行耦合，可以得到施工区域的结构面分布状况，同时在不同的区域对块体分布进行统计，包括块体的体积、埋深和密集度等，并在不同的条件下分析块体的稳定状况，为不同区域的块体支护提供参数指导．

1 岩体结构三维地质建模

1.1 耦合裂隙网络的岩体结构精细建模

Baecher圆盘模型[19-20]广泛应用于结构面建模过程，但实际上由于岩体的各向异性使得结构面形状很难为圆盘状[21]．所以用多边形[22]代替圆盘表示结构面的方法也同样应用于结构面的构建过程中，且岩体具有明显的非均匀性和各向异性时，其结构面形状应为多边形[23]．基于NURBS曲面技术、BREP模型数据结构和不规则三角网技术，本文通过对多边形结构面模型的尺寸和角度重新进行设计，使得结构面模拟过程效率更高，结合蒙特卡洛模拟方法，实现了对裂隙结构面的3维模拟，建立了多边形离散裂隙网络的3维模型．

用蒙特卡洛方法对单个结构面的尺寸和角度进行模拟，其多边形结构的尺寸和角度是相互独立的，分别模拟多边形中心点到顶点连线的长度和此连线与水平方向夹角．首先对角度进行模拟，直接使用蒙特卡洛方法，会造成多边形边数减少，甚至生成三角形，不仅降低模拟效率，而且与实际状况不符．本文采用四边形、五边形和六边形三种多边形进行模拟，生成三种多边形的概率相等．

假设多边形边数为，将[0，2,π]的环形区域进行等分，使多边形的每个顶点分别落在等分区间中，避免出现细长多边形，如图1所示．

图1 等分区间模拟

其次对多边形结构的尺寸进行模拟，利用圆盘与多边形结构的面积关系推求结构面尺寸的上、下界限．选取长度为的迹线进行模拟，圆盘直径1与迹线长度转换关系[24]为

   (1)

图3 单个结构面尺寸和角度模拟

单个结构面模拟完成后，还需对结构面位置、倾向、倾角等地质信息分别进行模拟，并按照位置信息将单个结构面输入，建立离散裂隙网络模型；之后根据坐标位置，耦合三维裂隙网络模型和工程地质结构模型．

1.2 基于三维耦合模型的块体识别

Li等[25]提出了单个随机块体建立的基本原则，首先删除无效的点、线，将共点的线互相连接，形成封闭曲线；之后用有效点的坐标位置推求封闭曲线信息，确定封闭曲线在曲面上的位置；接着用样条插值法在封闭曲线中建立曲面，并将曲面通过位置坐标进行耦合，封闭空间即所要求的块体；最后重复以上步骤直至识别所有块体，如图4所示．

图4 随机块体识别流程

2 随机块体支护几何参数计算

因空间位置和地质属性的影响，不同区域的块体分布情况不同．因此根据坐标信息和地质属性信息对工程地质模型进行划分，将地质属性相似的研究对象划分为相同的地质区域．对不同区域的支护参数进行统计分析，可获得块体的不同分布情况．对研究区域进行划分，有助于制定不同的支护方案，可以有针对性地解决随机块体对工程造成的不良影响．

2.1 块体密集度计算

块体密集度是指每个区域单位体积内块体的个数，单位体积内块体密集度对支护设计影响很大，是制定支护措施的一个重要参考指标．经过多次模拟，比较各个区域块体密集度的大小，可以得到统计意义上的块体分布情况，对于制定针对性的支护措施有重要作用．块体密集度的计算式为

   (2)

2.2 块体的埋深与体积

块体的埋深指的是块体与开挖面的距离，对于设计锚杆长度有重要意义，而且在一定埋深下的块体对出露块体的安全系数有一定影响．由于块体的形状不规则，此处统一选择块体距离开挖面的最远距离为块体埋深．

在随机块体识别过程中，所有块体的体积均可计算，并且把块体体积大小作为评价岩体稳定的一个重要指标．利用块体体积可以对洞室支护进行参数化指导，针对不同情况采取相应的支护措施．

块体体积计算采用Gauss-Legendre求积公式计算，即

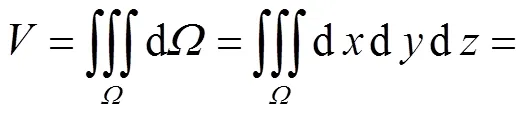
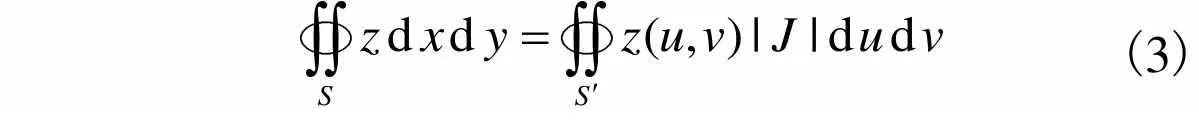
     (3)

3 随机块体支护动力参数计算

本文分别计算在自重和地震下块体的稳定系数，考虑主滑面的摩擦力及黏聚力和侧滑面的黏聚力，其他作用力对块体稳定系数影响较小，不考虑其作用．

3.1 块体运动方向及稳定系数

块体的运动模式主要有3种：块体脱落、单面滑动和双面滑动．

(1)块体脱落时，运动方向与作用力方向相同，为垂直向下，稳定系数等于0．

(2)当块体沿某个结构面运动时，滑动方向为合外力在此结构面的投影，稳定系数的计算式为

   (4)

式中：0为滑动面的摩擦系数；0和c分别为主滑面和侧滑面的黏聚力；N、T分别为合力法向和切向的分量．

滑动方向计算式为

   (5)

式中：为块体单面滑动的滑动方向；为垂直主滑面的单位法向量；为合外力．

(3)当块体沿双面滑动时，稳定系数的计算式为

   (6)

式中：f为滑动面的摩擦系数；c和c分别为主滑面和侧滑面的黏聚力；N、T分别为合力法向和切向的分量．

滑动方向计算如式(7)所示．

   (7)

式中：为块体双面滑动的滑动方向；底、为垂直两个滑面的单位法向量；是合外力．

自重工况和地震工况下合外力分别如式(8)和式(9)所示．

   (8)

   (9)

3.2 块体失稳概率

对每个块体的稳定系数进行计算，得到所有块体的安全系数值，并按照式(10)计算块体的失稳概率．

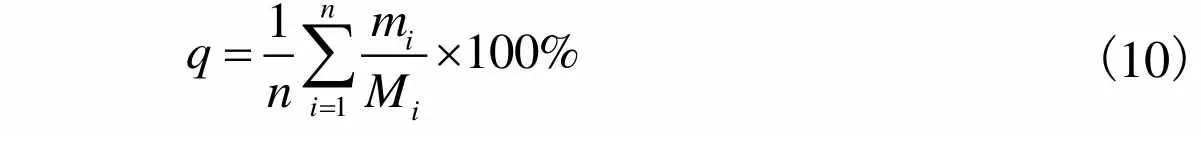
   (10)

式中：为块体失稳概率；表示失稳块体总数目，表示总的块体数目．

3.3 块体支护强度

目前在施工中直接通过计算支护强度来进行喷锚设计的方式较少，但支护强度是衡量支护设计的一个直接参考指标，对于保证工程安全有重要的意义．针对上文提出的3种块体运动模式，分别提出在块体不同运动模式下的支护强度计算方式，如式(11)～(13)所示．

(1)块体脱落时块体支护强度为

   (11)

(2)锚杆方向通常不与块体滑动方向平行，而是有一定的夹角，无论是单面滑动还是双面滑动，一般认为锚杆方向与出露面垂直，并将支护力方向与滑动方向的夹角设为，因此单面滑动时块体支护强度为

   (12)

(3)双面滑动时，支护强度为

   (13)

式中：为单位面积的支护力，即支护强度；为块体出露方向和滑动方向的夹角；0为单个锚杆支护的面积．

图5为随机块体支护动力参数计算流程，、分别为滑动面的摩擦力和黏聚力．

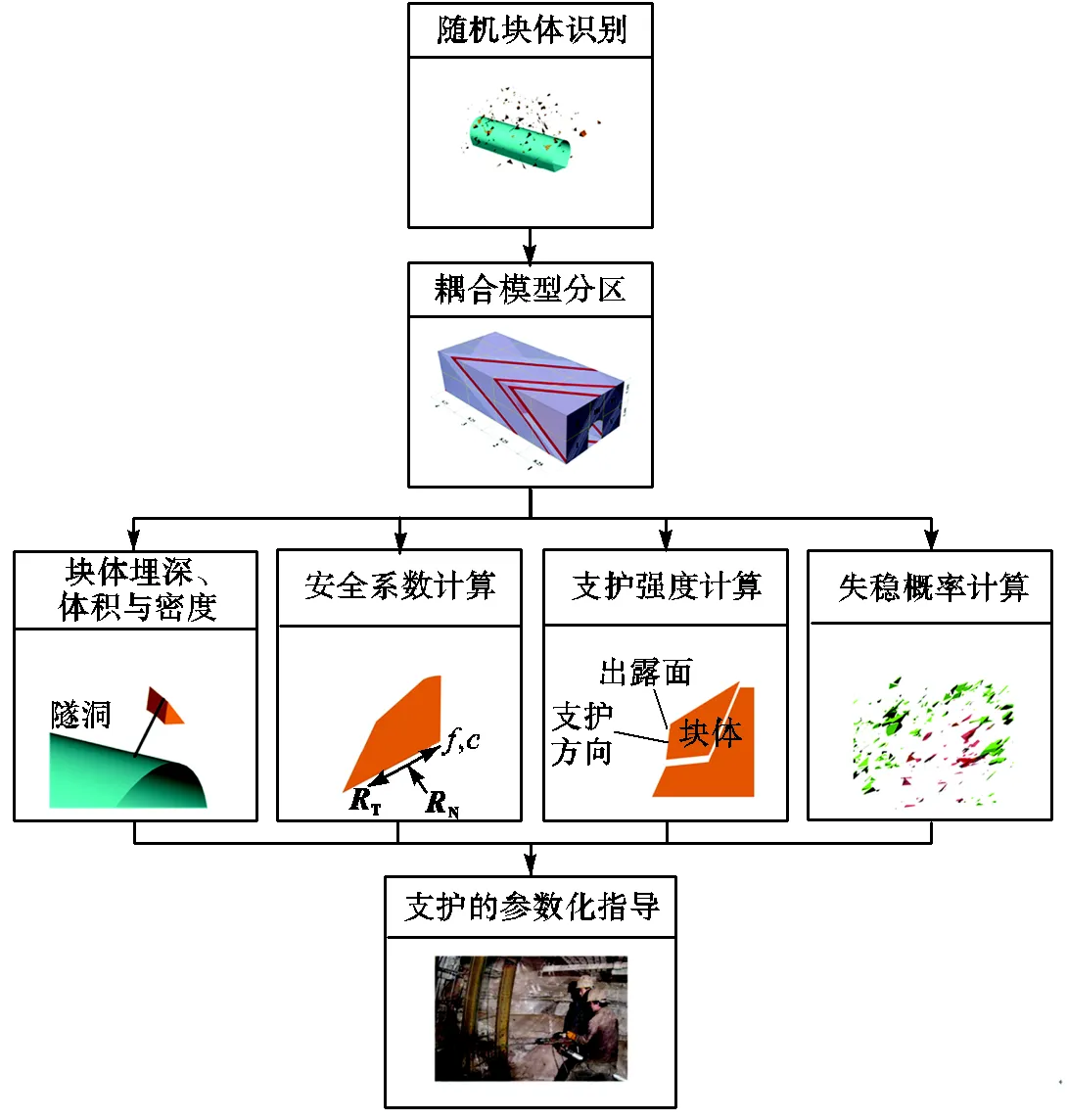
图5 随机块体支护动力参数计算流程

4 工程应用

4.1 工程概述

某水电站工程取水隧洞穿过电站左岸山体，工程区地面高程为265～730,m，相对高差约100～370,m，最高点高程735.5,m；以最高点高程为界线，其北坡坡度较小且平缓，坡角均小于30°，陡崖仅在比较大的冲沟的局部位置发育．其南坡主要是反向坡，由陡坡和斜坡相间组成．

取水隧洞沿线分布有夹层和节理裂隙，此外还有断层与洞线相交．岩层走向沿洞室方向由NW向NE偏转，倾角逐渐减小．其中，进口段岩层产状为340°～350°/NE∠21°～23°，隧洞中部岩层产状为60°～70°/NW∠14°～18°；隧洞后段岩层产状为45°～55°/NW∠15°～19°，洞室围岩等级主要是IV级．

隧洞附近主要发育有3组优势节理裂隙，在隧洞进口段各组节理裂隙的产状分别是70°～85°/NW∠60°～75°、290°～300°/NE∠65°～80°和315°～330°/NE∠45°～60°，裂隙迹长一般为0～4,m．

本文选取隧洞进口段33,m内裂隙为研究对象，对隧洞中随机块体的支护进行了分析．

4.2 岩体结构耦合建模

取水隧洞为城门洞形，高5,m，宽4,m，迹线分布统计参数如表1所示，由于隧洞以下岩体结构对稳定性分析无影响，建模过程中不再考虑．根据迹线统计参数建立隧洞岩体结构和离散裂隙网络耦合模型，如图6所示．图中断层与隧洞相交．

建立耦合模型后，取左侧洞壁迹线并向竖直方向投影，若模拟裂隙迹线图与实际裂隙迹线图二者结果一致，则认为模拟的结果正确，若二者不一致，则重新模拟，本文采用了从桩号0＋000到0＋30范围内的裂隙迹线进行验证，如图7所示．

表1 迹线统计参数

Tab.1 Statisticparameters of trace length

4.3 随机块体区域划分与分析

根据断层位置、块体位置和块体的运动方式在开挖面上分为Ⅰ～Ⅴ共5个区域，其中Ⅰ、Ⅲ、Ⅴ区域可能有块体出露，Ⅰ、Ⅲ区域的块体运动方式以滑动为主，Ⅴ区域块体运动方式主要是脱落，Ⅱ、Ⅴ区域岩体虽不出露，但可能受到其他区域的影响，也需要对其参数进行统计，如图8所示，在洞室方向分为1、2、3、4共4段，主要是考虑洞长及单元长度应为迹长的2～3倍，能包含完整结构面，洞室方向的区域划分可以在多次模拟中寻找块体聚集的区域．考虑位置信息的同时，应该让断层穿过更多的区域，比较断层在不同区域对稳定性的影响．

图7 模型验证

图8 隧洞区域划分(单位：m)

隧洞围岩和裂隙的力学参数如表2所示，地震的加速度采用文献[26]中的数值．

表2 联邦围岩及结构面参数

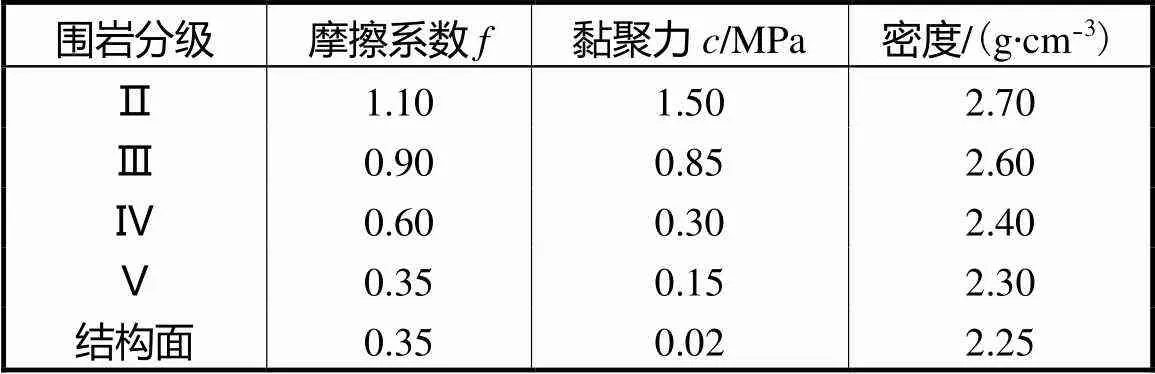
Tab.2 Parametersof rock and fracture

共进行块体分布模拟150次，其中10次块体模拟结果和稳定分析如表3所示．从表3中可以看出块体的平均体积较小，说明较大块体出现的情况不多；只受重力情况下块体的失稳概率较低，为15%,～25%,；在重力和地震力的双重作用下，失稳概率上升，为30%,～40%,，说明地震作用非常不利于块体的稳定．

表3 随机块体的10次模拟结果

Tab.3 Tentimes of statistical results of simulated stochastic rock blocks

通过150个随机块体模拟，在表4中对不同分区的块体埋深、块体数目、块体密集度和支护强度进行了统计分析．块体埋深和支护强度取模拟中的最大值，块体数目和块体密集度取模拟中的平均值．随机块体的埋深一般在1.00～1.90,m，对于锚杆长度设计有重要的参考意义；由于Ⅲ区的开挖面为圆弧，表面积更大，更容易与断层和裂隙互相切割形成块体，所以Ⅲ区的块体数目和块体密集度总体来说高于其他区域；其中Ⅲ-1区块体密集度明显高于其他区域，可能是由于有两条断层穿过，生成的随机块体更多；同时，断层对于Ⅱ、Ⅳ区域也有影响．另外由于Ⅲ区块体受重力影响最大，支护强度也远远高于Ⅰ、Ⅴ区域，而Ⅰ、Ⅲ区域支护力的差异主要来自裂隙产状的不同，裂隙倾角越大，需要的支护力也越大．

根据表3中和表4中的结果，在每个分区可以有针对性地进行支护，根据不同情况制定更灵活的支护措施；同时也可以通过计算对已支护的位置区域进行检验，可以较为精确地对支护措施进行评价，保证工程顺利地进行．

表4 随机块体几何参数分区统计

Tab.4 Partitioned statistical results of stochastic blocks geometric parameters

5 结 语

通过蒙特卡洛模拟方法建立多边形离散裂隙网络模型，同时耦合工程地质模型，生成了随机块体；根据空间位置和地质属性信息，对耦合模型了进行分区，然后在每个区域对随机块体的埋深、体积和密集度进行了统计，并对随机块体运动方向、稳定系数和支护强度进行计算；通过多次模拟，选择模拟过程中的不同数值，并在每个区域分别计算影响支护措施的参数，为支护设计提供数据支持，同时也可以用于检验已支护区域的稳定性．本文提出的方法是从地质结构的几何信息出发，利用统计规律对支护措施进行分析，与直接进行力学计算相比更加简便快捷，可以为支护设计、支护检验提供新的方法．

［1］ Goodman R E，Shi G H.[M]. New Jersey：Prentice-Hall，1985.

［2］ Zheng J，Deng J，Zhang G，et al. Validation of Monte Carlo simulation for discontinuity locations in space[J].，2015，67：103-109.

［3］ Elmouttie M K，Poropat G V. A method to estimate in situ block size distribution[J].，2012，45(3)：401-407.

［4］ Sturzenegger M，Stead D，Elmo D. Terrestrial remote sensing-based estimation of mean trace length，trace intensity and block size/shape[J].，2011，119(3)：96-111.

［5］ Hekmatnejad A，Emery X，Vallejos J A. Robust estimation of the fracture diameter distribution from the true trace length distribution in the Poisson-disc discrete fracture network model[J].，2018，95：137-146.

［6］ Han X，Chen J，Wang Q，et al. A 3D fracture network model for the undisturbed rock mass at the Songta dam site based on small samples[J].2016，49(2)：611-619.

［7］ 岳 攀，钟登华，吴 含，等. 基于 LHS 的坝基岩体三维裂隙网络模拟[J]. 水力发电学报，2016 35(10)：93-102.

Yue Pan，Zhong Denghua，Wu Han，et al. Simulations of 3-D fracture networks in rock mass of dam foundation using Latin hypercube sampling[J].，2016，35(10)：93-102(in Chinese).

［8］ 张 奇，王 清，阙金声，等. 基于凝聚层次聚类分析法的岩体随机结构面产状优势分组[J]. 岩土工程学报，2014，36(8)：1432-1437.

Zhang Qi，Wang Qing，Que Jinsheng，et al. Dominant partitioning of discontinuities of rock masses based on AGNES[J]，2014，36(18)：1432-1437(in Chinese).

［9］ Zhan J，Xu P，Chen J，et al. A stepwise approach for 3D fracture intersection analysis and application to a hydropower station in Southwest China[J].，2016，89：116-128.

［10］ Guo L，Li X，Zhou Y，et al. Generation and verification of three-dimensional network of fractured rock masses stochastic discontinuities based on digitalization[J].，2015，73(11)：7075-7088.

［11］ Hyman J D，Karra S，Makedonska N，et al. DFNWorks：A discrete fracture network framework for modeling subsurface flow and transport[J].，2015，84：10-19.

［12］ Xu C，Dowd P. A new computer code for discrete fracture network modelling[J].，2010，36(3)：292-301.

［13］ Hadgu T，Karra S，Kalinina E，et al. A comparative study of discrete fracture network and equivalent continuum models for simulating flow and transport in the far field of a hypothetical nuclear waste repository in crystalline host rock[J].，2017，553：59-70.

［14］ Makedonska N，Hyman J D，Karra S，et al. Evaluating the effect of internal aperture variability on transport in kilometer scale discrete fracture networks[J].，2016，94：486-497.

［15］ Xu C，Dowd P A，Wyborn D. Optimisation of a stochastic rock fracture model using Markov chain Monte Carlo simulation[J].，2013，122(3)：153-158.

［16］ Zhang Q H，Wu A Q，Zhang L J. Statistical analysis of stochastic blocks and its application to rock support[J].，2014，43：426-439.

［17］ Li M C，Zhou S B，Wang G. 3D identification and stability analysis of key surface blocks of rock slope[J].，2016，22(4)：317-323.

［18］ Zhong D H，Li M C，Song L G，et al. Enhanced NURBS modeling and visualization for large 3D geoengineering applications：An example from the Jinping first-level hydropower engineering project，China[J].，2006，32(9)：1270-1282.

［19］ Baecher G B，Lanney N A，Einstein H H. Statistical description of rock properties and sampling[C]//18(). Golden，USA，1977：1-8.

［20］ Einstein H H，Veneziano D，Baecher G B，et al. The effect of discontinuity persistence on rock slope stability [C]//. Pergamon，Turkey，1983：227-236.

［21］ 周维垣，杨若琼，尹健民，等. 三维岩体构造网络生成的自协调法及工程应用[J]. 岩石力学与工程学报，1997，16(1)：29-35.

Zhou Weiyuan，Yang Ruoqiong，Yin Jianmin，et al. Three dimensional joint network in rock mass using self adjusted method and engineering application[J].，1997，16(1)：29-35(in Chinese).

［22］ Dershowitz W S，Einstein H H. Characterizing rock joint geometry with joint system models[J].，1988，21(1)：21-51.

［23］ 张贵科，徐卫亚. 裂隙网络模拟与REV尺度研究[J]. 岩土力学，2008，29(6)：1675-1680.

Zhang Guike，Xu Weiya. Analysis of joint network simulation method and REV scale[J].，2008，29(6)：1675-1680(in Chinese).

［24］ Ni P P，Wang S H，Wang C G，et al. Estimation of REV size for fractured rock mass based on damage coefficient[J].，2017，50(3)：555-570.

［25］ Li M C，Liu J，Liu F，et al. Method for identifying and analyzing 3D surface blocks of rock mass structures[J].，2013，139(10)：1756-1764.

［26］ 徐栋栋，邬爱清，卢 波，等. 基于地震时程曲线的块体动安全系数计算[J]. 长江科学院院报，2011，28(11)：67-71.

Xu Dongdong，Wu Aiqing，Lu Bo，et al. Calculation of block dynamic safety factor based on seismic time history curve[J].，2011，28(11)：67-71(in Chinese).

(责任编辑：王新英)

Stability Analysis of Stochastic Rock Blocks Based on Three-Dimensional Fracture Network Rock Mass Structure Model

Li Mingchao1，Zhang Ye1，Zhou Sibao2

(1．State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300354，China；2．Zhejiang Design Institute of Water Conservancy and Hydroelectric Power，Hangzhou 310002，China)

Based on Monte Carlo simulation method and 3D geological modeling technology，a rock mass structure model with polygonal discrete fracture network was reconstructed and the identification of stochastic rock blocks was conducted．Then，a new approach of stability and support analysis for stochastic rock blocks of tunnels was presented．The model was divided into several subareas according to positions and geological attributes．And the depths，the volume and tensity of blocks were calculated to study the rule of block distribution in each subarea．The instability probabilities and support intensities of stochastic rock blocks under self-weight and seismic condition were calculated as well．These parameters contribute to the determination of the bolt spacing，lengths and support force of single bolt and provide parametric guidance to design a support scheme of stochastic rock blocks in the tunnel．Meantime it can also be used in support scheme test．This method has been applied to the stability support of an intake tunnel.

rock mass structure；3D geological model；polygonal discrete fracture network；stochastic rock block；stability analysis；support intensity of rock blocks

10.11784/tdxbz201703059

TU457

A

0493-2137(2018)04-0331-08

2017-03-21；

2017-05-26.

李明超（1979—  ），男，博士，教授.Email：m_bigm@tju.edu.cn

李明超，lmc@tju.edu.cn.

国家优秀青年科学基金资助项目(51622904)；国家自然科学基金资助项目(51379006).

the National Natural Science Foundation for Excellent Young Scientists(No.,51622904)and the National Natural Science Foundation of China (No.,51379006).