直面 点拨 体验 归纳——谈谈小学数学小组合作学习的四重境界

浙江湖州市安吉县实验小学　　王孝华

在我们的教学过程中，总是有部分学生处于“被间接忽视”的境地。运用小组合作的形式组织教学，不仅可以加强师生、生生之间的交流，还有利于调动学生的主动性，发挥群体活动的优势，促进个人的发展。笔者在小组合作学习教学实践时，一次偶然的机会，欣赏到宋代禅宗大师青原行思提出的参禅的三重境界：看山是山，看水是水；看山不是山，看水不是水；看山仍是山，看水仍是水。寥寥数语之中，就将人之一生，从垂髫小儿至垂垂老者，匆匆人生旅途道了个一清二白。然禅宗之慧，个中奥义，非我等凡夫俗子可以参透，仅作茶余饭后偶思为用。可不经意间，将此三重意境与小组合作学习结合起来，发现此禅语与自己的课堂教学亦有相通之处。细品之，可从原本禅宗悟佛的三重境界，转化为小组合作学习的四重境界，即“山是山，水是水”直面式小组合作学习；“山非山，水非水”点拨式小组合作学习；“山似山，水似水”体验式小组合作学习；“山仍是山，水仍是水”归纳式小组合作学习。

一、第一重境界：“山是山，水是水”直面式小组合作学习

《义务教育数学课程标准（2011年版）》指出：“要引发学生的数学思考，充分考虑数学的本身特点，体现数学的实质。”“数学的实质”是什么？数学是一门基础学科，是一种工具学科！让学生在数学课堂上掌握一定的技能，并能运用这些技能去解决生活中遇到的实际问题，才是我们数学教师的教学目的。为提高课堂教学效率，我们在追求丰富多彩的教学方式的同时，不能放弃对数学本质的追求。

如人教版数学五年级上册《小数乘小数》：

1.知识准备部分（3分钟）

（1）笔算，说说25×17你是怎么笔算的？

（2）完成表格，你发现了什么？

因数　14　140　1400因数　2　2　2积

2.自主探究部分（10分钟）

我们上课用的课堂作业本4.7元一本，买5本多少钱？

如果这样的课堂作业本要买7本，该怎么算？8本呢？

……

原本也想在导学案中加入生动的情境设计，再配上主题图，但在追求“开门见山”的思想指导下，简化为两个层次的设计：首先让学生先完成“知识准备部分”第1小题的小组交流，归纳整数乘法的计算方法，再配上第2小题的表格计算，强化学生头脑中积的变化规律。然后在“自主探究部分”，让学生运用学到的知识来解决生活中的实际问题。学生发现，数学学习很有用。

中科院院士李大潜先生也曾对学生数学学习的本质有过评价：“数学学习的本质是提高素质。”学习数学，可以让学生数量观念更好，逻辑思维能力更强，讲话做事更有条理。培养学生认真负责、精益求精、一丝不苟、不断创新等数学品质，才是我们数学教师的最终目标。所以，在教学中直面数学技能教学，引导方法归纳，形成学习技能，并让学生运用技能来解决生活中的实际问题，没有“云山雾罩”，没有“花言巧语”，有的只是——“山是山，水是水”！

二、第二重境界：“山非山，水非水”点拨式小组合作学习

《义务教育数学课程标准（2011年版）》指出：“有效的教学过程是学生学与教师教的统一，学生是学习的主体，教师是学习的组织者、引导者与合作者。教师要以平等、尊重的态度鼓励学生积极参与教学活动，启发学生共同探索，与学生一起感受成功和挫折，分享发现和成功。”教师不应该成为教学过程中的“山”，学生更不应该成为“水”。教师应该让课贴着学生的思维前行，让课堂成为教师和学生最和谐最美好的乐章。而教学内容中的重点和难点，又成为学生学习中不可避免的“拦路山”。以小组合作学习模式来组织教学，学生在这个平台上自由发挥，有很大的主动性，但在小组合作学习模式中，也存在着太多的不可预见性，我们不能预设学生的学习会走到哪儿，会提出什么令人吃惊的问题，生成的课堂会有多少的不可思议，我们只能努力尝试让学生学会“爬山”，让教师的点拨和课堂成为围绕着“山”转的“水”。

在教学《平行四边形的面积》一课时，如下设计：

1.知识准备（略）

2.探究新知

测量下图中平行四边形的有关数据（保留整数），尝试计算该图形面积。

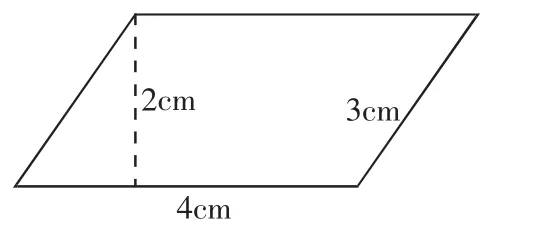
在独学环节巡视时，发现以下三种情况：生1：4×3=12（平方厘米）。生2：4×2=8（平方厘米）。

生3：（4+3）×2=14（平方厘米）。

当展示完这三种不同的算法后，围绕着三座“山”，教师开始了点拨引导。

生1：我觉得平行四边形和长方形差不多，长方形是用长×宽求面积的，我也就用4×3了。

师：先不论这种想法是否正确，他将新知识与旧知识进行比较，然后得出自己的结果，这也是一种很好的思考方法。

生3：老师，我的想法好像有问题，我的（4+3）×2是计算它的周长，不是面积。

师：平行四边形周长的算法我们也没有学过，你是怎么想的？

生3：周长是图形一周的长度，和长方形一样，平行四边形由四条边组成，它的周长就是四条边的和。

师：能够主动运用已经掌握的知识来解决新问题，你真的很棒，但是希望以后你在审题方面再多努力。

生2：老师,我觉得平行四边形是容易变形的四边形，我就把它变成长方形……

师：你能告诉我们，你是怎么样变的吗？

生2：我上来讲吧，我把这边割下来，补到右边去。这样就变成了长方形。

师：真棒，你把它转化成我们学过的长方形，然后再来求面积。

……

从主动寻求与已知知识之间的联系，到完成平行四边形周长的探索，再主动地出现“转化”的思想，这些不能预设的“闪亮点”，成为课堂教学过程中一座座“风景迷人”的“山”，面对这些“拦路山”，学生有迷茫，有争论。而教师的引导，就好比是拦路山下“温情的水”，一句提醒，一个手势，一次比画，山不再是原来的那山，水也不再是原来的那水了。

三、第三重境界：“山似山，水似水”体验式小组合作学习

合作学习是小组成员在同一段时间内针对同一内容进行的学习活动。由于个体之间存在的差异性，对同一个问题的思维水平必然有高有低。所以在教学过程中，教师不必担心学生们那“似是而非”的学习结果，只要在提出共同要求的同时，去创造机会，提供平台，让学生自己发表不同的意见。在这样的体验学习的过程中，组内每个层次的学生都能发挥自己的优势，真正实现共同学习。

在教学《稍复杂的方程2》时，直接选用了课本上的例题2作为教学素材：

苹果和梨各2千克，共10.4元。已知梨每千克2.8元，苹果每千克多少钱？

当我提出用两种方法解答这一题后，有一个小组汇报如下：

生1：第一种方法，数量关系式是：苹果的钱+梨的钱=总共付的钱，方程是2x+2.8=10.4；第二种方法，数量关系式是：（苹果的单价+梨的单价）×2千克=共付的钱，方程是2（x+2.8）=10.4。

生2：老师，我来补充。按照他的方程来计算，发现两个答案是不一样的。肯定有错误。

师：你这么快就发现问题了，而且能马上断定有错误，学习效率真高。

生3：我来补充一下，第一种方法中，数量关系没错，只是方程列错了，2x是表示苹果的总价，但是2.8只是梨的单价，梨也买了2千克，要表示梨的总价，应该是2.8×2。

……

《义务教育数学课程标准（2011年版）》特别提出了要让学生“获得基本的活动经验”。在学习过程中，学生会因为种种原因，对事物的认知有这样或那样的困惑，这正是学生在“山似山，水似水”的感觉中徘徊。学生能够对这些错误主动地进行理性思考，找出错误根源，并加以纠正，才是最珍贵的。在学生体验学习过程、经历学习错误、感知错误原因时，教师要敏锐地抓住学生这种暴露思维错误的瞬间，帮助他从“朦胧烟雨”中走出来。

四、第四重境界：“山仍是山，水仍是水”归纳式小组合作学习

这重境界追求的是一种返璞归真，有一种“只可意会，不可言传”的味道。当学生对数学认知积累到一定程度，不断地反省、琢磨后，会逐渐对数学知识体系有一个初步的认识，认识到数学知识之间存在着的联系。在学习交流时，每个组员的局部描述，会在一些学生的头脑里形成一棵树、一幅图、一张网。

以人教版《小数除法》的单元复习为例，设计了下面几道独立练习（保留一位小数）：

这几道基本的小数除法题目中，有最高位不够除的、商是循环小数的、商要保留规定小数位数的、商中间有0的、除数扩大后被除数要添0补位的，基本上囊括了本单元的主要题型，以前教学时都是一个个独立教学的，各个知识点之间虽有联系，但学生的感触却不深。教师在教学这部分内容时，努力尝试让学生在原有基础上形成一个完整的小数除法计算方法的知识体系。所以在学生独立完成后，教师就引导学生完成如下图所示的“知识树图”，形成小数除法部分完整的知识体系。

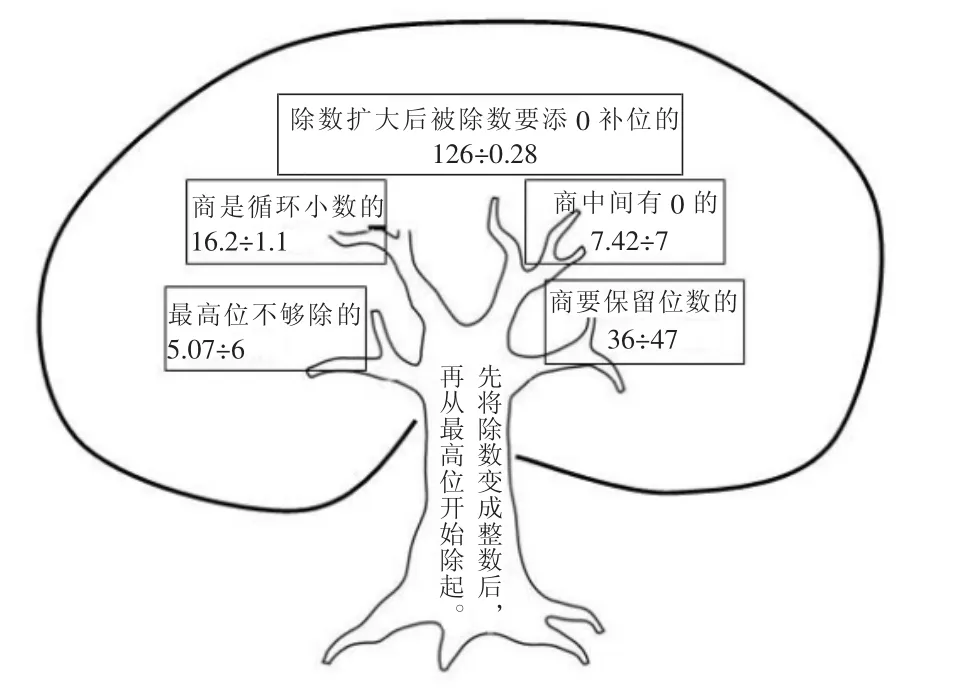
在学生头脑中，那些孤立、单独的知识点带来太多的学习难度，学习过程中往往会顾此失彼。在小组合作时，学生自由交流着自己的看法，“仁者见山，智者见水”。教师引导着学生去仔细地“看山赏水”，尽管“山不同脉，水不同源”，但是可以发现，“山有山向，水有水路”。当学生们再回首，看山还是山，看水还是水，只是这山这水，在他们的眼里，已有另一种“内涵”了。

教育的真正意义在于发现人的价值，发掘人的潜能，发挥人的个性，而一切教学因素最终是作用于学生，教学归根结底是学生的学，谁也无法替代。德国教育学家第多斯惠也曾说过：“教学的艺术不在于传授本领，而在于激励、唤醒、鼓舞。”所以在小组合作学习中，无论是到达上面哪一重境界，所追求的都是立足学生的主体地位，教师应该根据学生的发展需求，抓住学习思维活动的热点和焦点，激发认知冲突，引起学生主动思考，从而获得基本活动经验，理解基本数学思想。♪