求解动力学问题科学素养的培养

■湖南省汨罗市一中　

一、析题破题能力的培养

物理的学习特别强调分析、推理和建模能力的培养,以及对挖掘题目隐含条件以便找到解决问题的突破口等破题能力的培养。

例1 如图1甲所示,一物块在t=0时刻滑上一固定斜面,其v-t图像如图1乙所示。若重力加速度和图中的v0、v1、t1均为已知量,则可以求出的物理量有哪些?

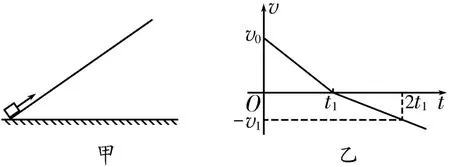
图1

析题:纵观近几年的全国高考试题可以发现,以图像的方式考查牛顿第二定律是一类很重要的题目,此类问题要求考生具备理解图像所给信息和破译图像信息的能力。图像的形式以v-t、a-t、F-t图像居多,其中考查最多的是v-t图像。题型既有选择题也有计算题,难度中等。

破题:图像类问题的实质是力与运动的关系,其中牛顿第二定律F=ma是纽带,明确图像的种类,以及图像的轴、点、线、截距、斜率、面积所表示的意义是前提。运用图像解决问题一般包括两个角度:(1)用给定图像解答问题;(2)先根据题意作图,再用图像解答问题。另外,在实际应用中有时还需要建立物理情景与函数、图像的相互转换关系。

解答:由v-t图像可求出物块沿斜面向上滑行时的加速度大小根据牛顿第二定律得mgsinθ+μmgcosθ=ma,即同理,物块沿斜面向下滑行时有联立以上两式解得可见能计算出斜面的倾斜角度θ、物块与斜面间的动摩擦因数。物块滑上斜面时的初速度v0已知,向上滑行过程为匀减速直线运动,末速度为0,平均速度为,所以物块沿斜面向上滑行的最远距离,物块沿斜面向上滑行的最大高度为

二、规范表达能力的培养

例2 如图2所示,质量m=2kg的小球以初速度v0沿光滑的水平面飞出后,恰好无碰撞地从A点进入竖直平面内的光滑圆弧轨道,其中B点为圆弧轨道的最低点,C点为圆弧轨道的最高点,圆弧AB所对的圆心角θ=53°,圆半径R=0.5m。若小球离开水平面运动到A点所用时间t=0.4s,取g=10m/s2(sin53°=0.8,cos53°=0.6),求:

图2

(1)小球沿水平面飞出时的初速度v0的大小。

(2)小球到达B点时,对圆弧轨道的压力大小。

(3)小球能否通过圆弧轨道的最高点C?说明原因。

解析:(1)小球在离开水平面运动到A点的过程中做平抛运动,有vy=gt。根据几何关系得,解得v0=3m/s。

(2)小球到达A点时的速度5m/s。小球在从A点运动到B点的过程中,根据机械能守恒定律得,解得vB=29m/s。设小球运动到B点时受到圆弧轨道的支持力为N,根据牛顿第二定律得,解得N=136N。由牛顿第三定律可知,小球对圆弧轨道的压力大小N'=N=136N。

(3)假设小球能通过圆弧轨道的最高点C,则小球在从B点运动到C点的过程中,根据机械能守恒定律得,解得vC=3m/s。在C点有F向=,所以假设成立。

规范答题小窍门:(1)叙述必要的过程、遵循的规律、假设的物理量;(2)题目中已有物理量符号的,一定要用题目中的符号表达方程,以免计算结果出错;(3)解题过程中,必要的几何关系不能少;(4)要尽量根据题设条件写出必要的方程,并求出相关物理量。

三、建模能力的培养

在应用机械能守恒定律处理实际问题时,经常会遇到“链条”“液柱”类的物体,其在运动过程中将发生形变,其重心位置相对物体也发生变化,因此这类物体不能再视为质点来处理。一般情况下,可将此类物体分段处理,确定质量分布均匀的规则物体各部分的重心位置,根据初、末状态物体重力势能的变化列式求解。

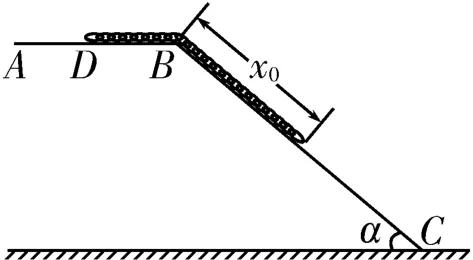
图3

例3 如图3所示,一条长为L的柔软匀质链条,开始时静止在光滑梯形平台上,斜面上的链条长为x0。已知重力加速度为g,链条总长L小于斜面长度BC,斜面倾角为α,试用x0、x、L、g、α表示斜面上链条长为x时链条的速度大小(链条尚有一部分在平台上且x＞x0)。

解析:由链条各部分和地球组成的系统机械能守恒,设链条的总质量为m,以平台所在位置为零势能面,当斜面上链条长为x时,有,解得

建模感悟:(1)利用等效法计算势能变化时,应根据物体的相对位置关系将物体分成若干段,并注意等效部分的质量关系;(2)解决涉及重力势能变化的问题时,物体的位置变化要以重心位置变化为准。

四、防范所谓的常规丢分的思维培养

例4 两颗卫星在同一轨道平面内绕地球做匀速圆周运动。地球半径为R,a卫星离地面的高度等于R,b卫星离地面的高度等于3R。则:

(1)a、b两卫星的运行周期之比Ta∶Tb是多少?

(2)若某时刻两卫星正好同时通过地面同一点的正上方,且已知a卫星的运行周期为Ta,则再经多长时间两卫星相距最远?

解析:(1)由牛顿第二定律和万有引力定律得,解得因此

(2)设再经过时间t两卫星相距最远,则,又有,解得

易错诊断:本题的易错点在于找不准何时相距最远,以及相距最远时应满足什么条件。两卫星相距最近是指两卫星位于地心的同侧,且与地心在同一直线上。当两卫星相距最远时,两卫星转过的弧度之差最小为π。若考虑周期性,则两卫星转过的弧度之差最小为kπ(k=1,3,5,…)。