基于融合先验方法的贝叶斯网络结构学习

高晓光, 叶思懋, 邸若海, 寇振超

(西北工业大学电子信息学院, 陕西 西安 710129)

0　引　言

概率论与数理统计为很多现代自然科学与工程问题的解决提供了有效的方法。贝叶斯网络作为一种概率图模型,其坚实的理论基础、知识结构的自然表述方式、强大的推理能力使其成为数据分析时强有力的建模工具,特别地在机器学习[1]、数据挖掘[2-3]、决策分析[4]等领域,已成为了一种重要的数学工具。

贝叶斯网络可以手工构造也可以从数据中学习,后者称为贝叶斯网络学习,现在随着人工智能的发展和应用情况的复杂化,如何有效地进行贝叶斯网络学习是研究的主要内容,其中结构学习是研究的热点。

贝叶斯网络结构学习是一个非确定性多项式困难(non-deterministic polynomial hard, NP-hard)问题[5],通常需要较大的样本量[6],但有些情况下只能获得比较少的数据[7],用这些小数据进行结构学习会造成学习误差大、决策不准确的后果。利用先验信息能够有效提高学习准确度[8],弥补数据量的不足[9]。

对于如何利用先验信息,有很多学者已经对此进行了研究,利用先验信息进行结构学习一般都使用评分搜索法,文献[10]对这些方法做了一定的总结。比较典型的是以下几种:文献[11]利用节点序作为先验信息,用K2算法进行学习;文献[12]利用边是否存在作为先验信息;文献[13]利用边存在的概率作为先验信息。

现有的文献都没有考虑到对错误不确定先验信息的适应能力,而在某些情况下,比如战场环境中应用贝叶斯网络需要较强的可靠性,且该环境下获得的数据量小,对专家先验信息的依赖比较大。所以当专家给出不正确的先验信息时,希望算法对错误有一定的适应能力,当先验信息有部分错误时,能够降低其对结果的负面影响。这样能够增强结构学习算法的可靠性和鲁棒性。

本文采用评分搜索的方法进行结构学习,在评分和搜索环节都利用了先验信息。首先本文提出了一种新的融合先验信息的评分函数,该评分函数融合先验信息的方式有两个特点:第一,当数据量越大时,评分先验项所占的权重越小;第二,评分函数的先验项可以任意构造,达到期望的要求。本文借鉴文献[14]中构造先验的思想,设置一个关于先验信息的惩罚项,当先验信息与当前网络的差距越大,距离越大,惩罚越大。先验项的另一种构造方法是计算先验部分的联合概率,但精确求先验部分的联合概率是很复杂的[15],本文提出的方法相对简单有效。

在搜索环节,本文从增强鲁棒性的角度出发提高对错误先验信息的适应能力:评分搜索算法很容易搜不到与先验信息有关的边,就达到局部最优,这样就造成了先验利用的不充分,当先验信息存在部分错误时,现有的评分搜索算法可能会学到这些错误先验信息有关的边,而忽略了正确先验信息的边,虽然概率比较小,但是说明现有的算法鲁棒性不够好。本文提出一种关于先验信息的引导策略,在搜索过程中增加了一个先验信息搜索算子,从而扩展搜索空间,最后能充分地利用正确的先验信息,这样就能增强鲁棒性,从而提高对错误先验信息的适应能力。

1　先验信息的表示方式

通常情况下,先验信息是专家对部分变量的主观认知,所以一般给出的是部分边存在的概率大小,而且专家也很难给出这些边的联合概率,能提供的是每条边存在的边缘概率。所以按照这种情况经行建模。

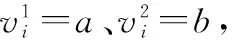
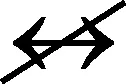
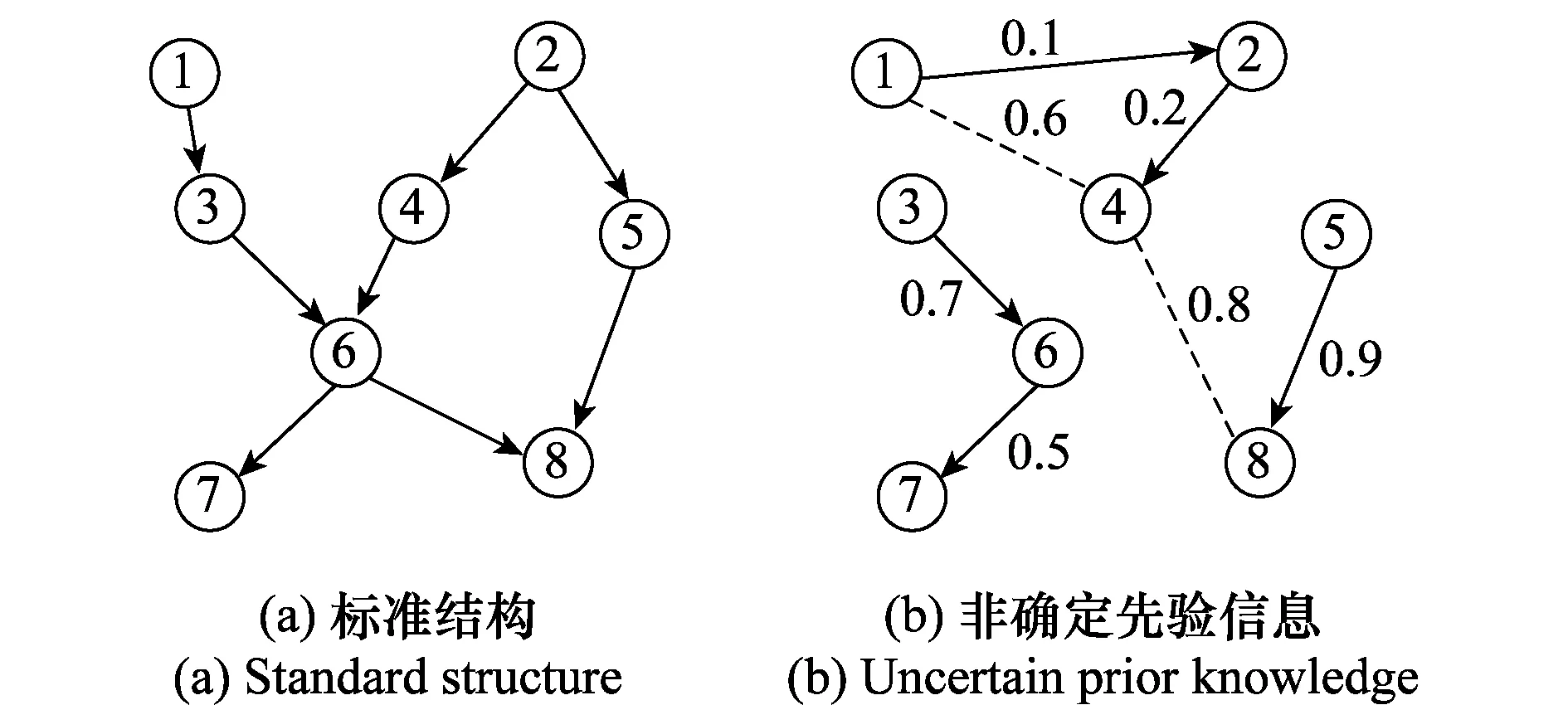
图1　先验信息实例

2　融合先验信息改进评分

本文要将先验信息融合到评分函数中去,在利用评分—搜索算法进行贝叶斯网络结构学习时, 对于结构,贝叶斯评分的模型为

lnP(G,D)=lnP(D|G)+lnP(G)

(1)

式中，lnP(D|G)项为对数据的似然度；lnP(G)项为结构G的先验信息概率,本文融合先验信息的方法是对lnP(G)进行估计,其充当了一个罚项,当先验信息与当前网络的差距越大,距离越大,惩罚值越大。

文献[14]为了利用确定性先验信息,提出一种先验信息分布的估计方法,设任意的网络结构Bs,先验信息ξ代表的贝叶斯网络结构为Bp,然后计算Bs的先验信息分布估计为

P(G)=P(Bs|ξ)=ckδ

(2)

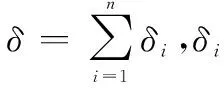
本文借鉴这种思路与模型,为了融合不确定先验信息,研究得到了一个新的评分模型。

本文将k替换为一个关于数据样本量的函数,将δ替换为一个关于概率取值的函数,就能得到一个处理不确定先验的模型。

已知先验信息ξ(V,P),其中包含n对节点。对于特定结构G,参照式(2)构造罚项为

(3)

式中,k(s)、εi(p)都是函数,其中s代表样本量的大小,p代表在G中某条边ei在ξ中对应的概率。对式(3)取对数并进行化简得

(4)

式中,C为常数,对任意的结构均相同,该项在比较过程中可以省略;K(s)是一个函数,记为数据权衡项;εi(p)中包含了先验信息,记为融合先验信息项。

2.1　数据权衡项的构造

对于贝叶斯网络结构学习,样本量较少时需要用先验信息来弥补样本的不足。随着样本量的增多,对先验信息的依赖会越来越弱,但错误的先验信息始终会影响学习结果。所以本文构造K(s)随样本量的增加而减小,这样在样本增多时,错误先验信息的影响会减小,具体函数为

(5)

式中,s为样本量;c和φ是一个可调的平衡因子,其取值可以根据要求解的贝叶斯网络结构的复杂度设定,一般的准则是,网络结构越复杂,φ的取值应该越大。当c取1,φ取不同值时对|K(s)|函数进行了仿真,如图2所示。

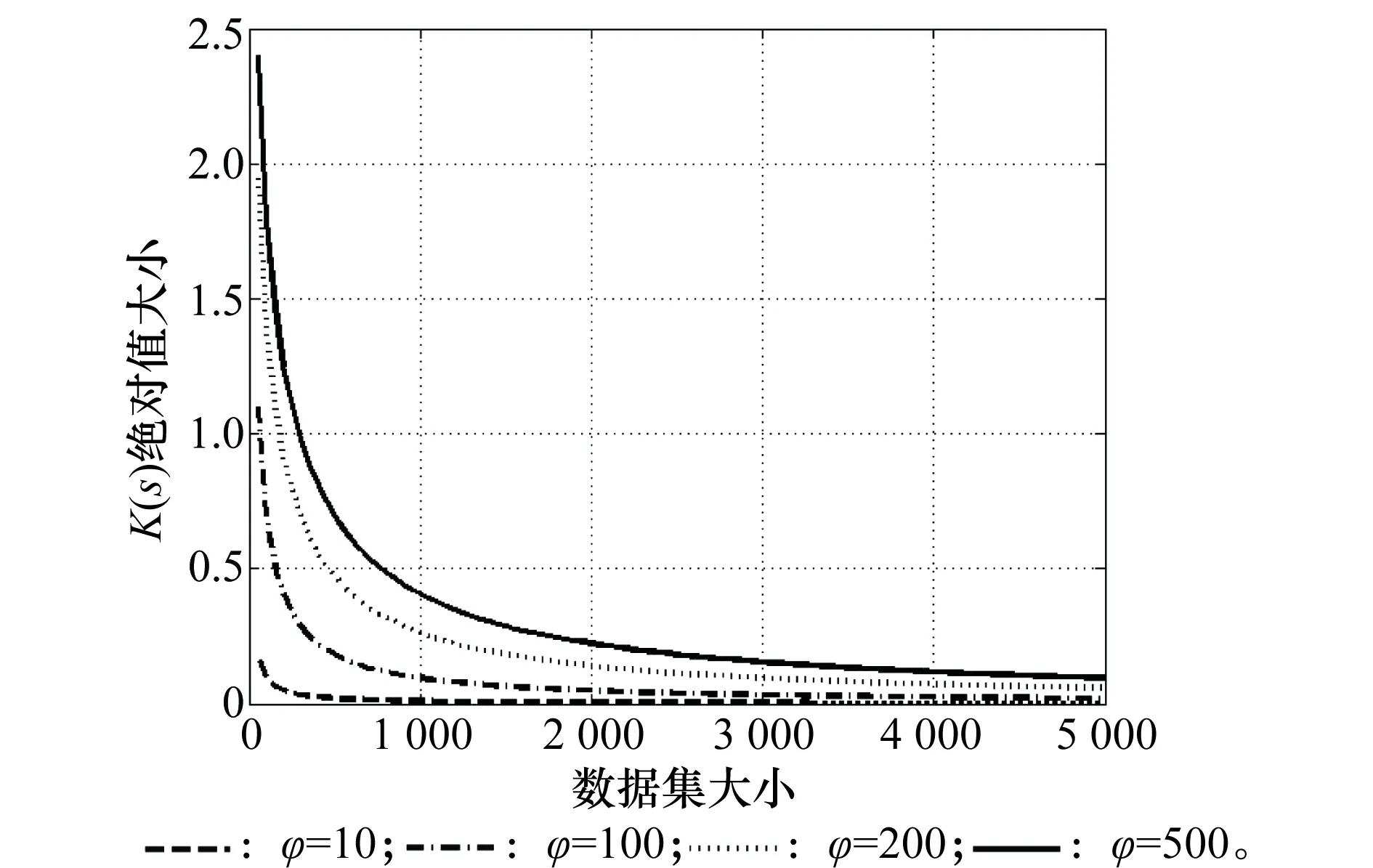
图2　φ取不同值时|K(s)|的大小

由图2可知,数据集越大,K(s)的值越小,先验所占的权值就越小。

2.2　融合先验信息项的构造

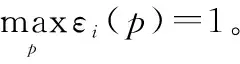
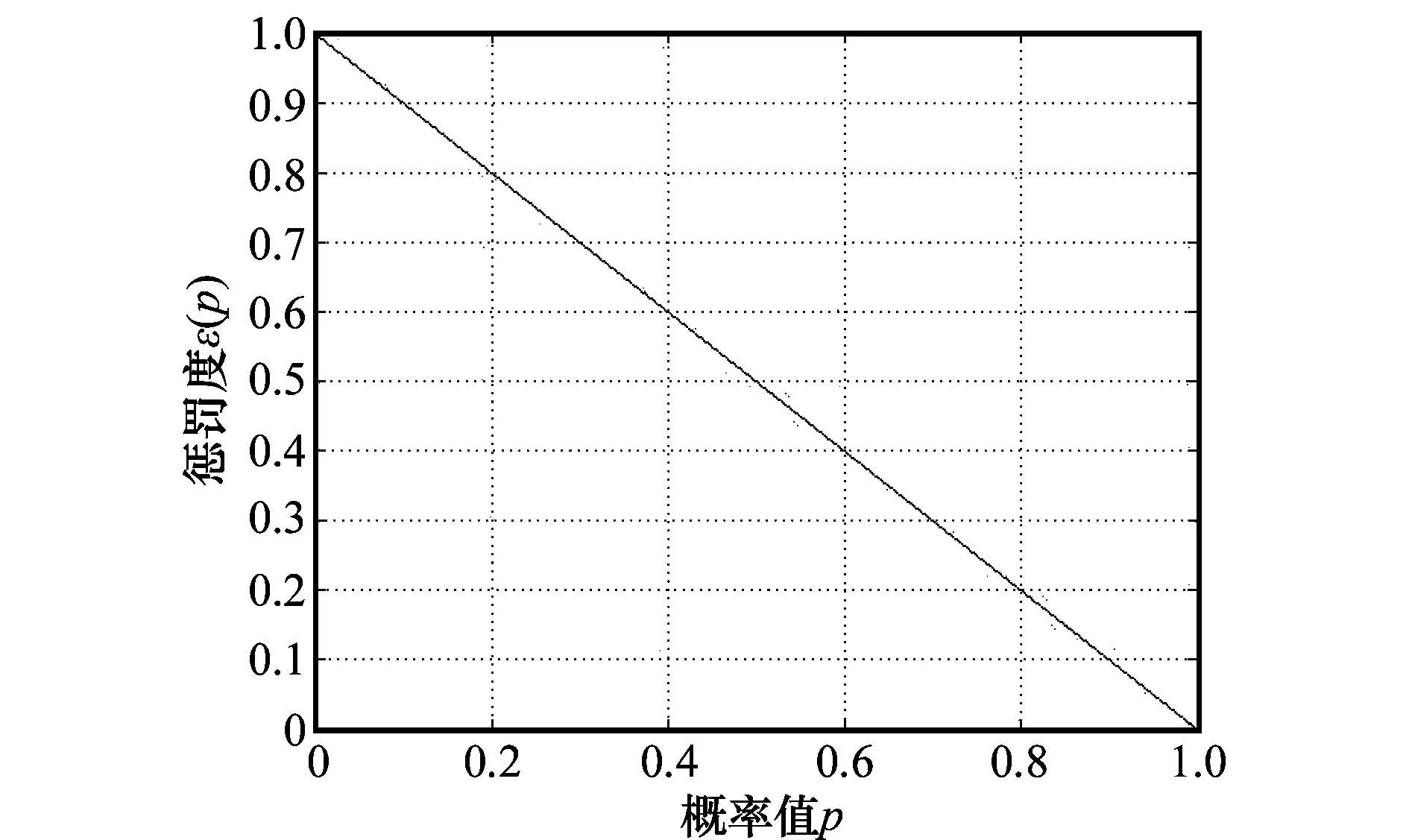
图3　线性罚项函数

这种线性函数有一个缺点,若先验信息有误则很容易学到错误的网络,为了克服这个问题,本文从信息论中不确定度的角度出发,利用熵的概念,构造一个非线性的罚项函数。思想是,若ei造成不确定度越大,罚项的变化就越小,即εi(p)的导数的绝对值越小。所以目标是构造导函数D(p),当不确定度达到最大值时,导数为0。将ei视为随机变量,则该随机变量的熵计算公式为

(6)

熵表示了这个变量的不确定度,熵越大说明ei的不确定度越大,ei一共有3种情况。不失一般性,对另外两种情况取均匀分布。

结合式(6)记

(7)

给出导函数公式

(8)

εi(p)应该满足条件

(9)

式中,k是一个常数。

进行数值积分后,εi(p)的函数图像如图4所示。

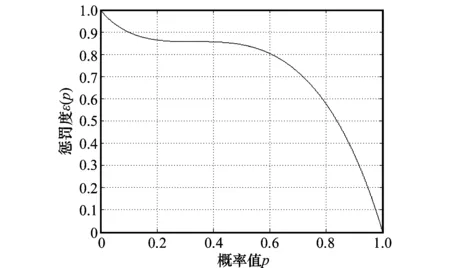
图4　基于熵的罚项函数

由图4可知,当专家先验信息给出的概率具有的不确定度越大,在此概率值附近的改变造成的影响就越小,比如概率为0.3和概率为0.6两处造成的惩罚度差值就很小,因为专家经验具有的不确定度很大。这样优点在于,若错误的先验信息不是很绝对,则其造成的影响较小。

3　融合先验信息的搜索过程

由于贝叶斯网络的结构学习是一个NP-hard的问题。在启发式搜索的过程中,随着节点数的增加,贝叶斯网的局部峰值会越来越多,容易陷入局部最优,在贝叶斯的结构学习中,虽然已经发展了很多的搜索算法,包括一些群智能算法,也很难搜索到全局最优解。这样在给出先验信息后,搜索算法很可能搜索不到先验信息中的那些边,尤其是那些概率取值比较大的边。此时当先验信息中有部分错误时,就可能会只用到那些错误的先验信息,使得学习结果很差,为了改善这种情况,本文在搜索过程中,增加了一个“先验搜索”算子,尽可能地利用正确的先验信息,这样能提高算法的鲁棒性,提高整体的学习效果水平。

先验信息搜索算子的设计思路为:搜索过程中,对先验信息中的每个节点对,都按照先验信息的概率进行置边,例如对于节点对vi对应的概率pi=[0.1,0.8,0.1],则这对节点间有0.8的概率置为正向。但是经过先验信息搜索算子的修改后,得到的结构可能会成环,所以要进行去环操作。

下面给出先验信息搜索算法和去环算法流程，如表1和表2所示。

表1　先验信息搜索算法流程

将先验搜索算子加入到爬山算法中得到先验搜索爬山(informed-search hill climbing,IS-HC)算法，流程如表3所示。

4　仿真结果及其分析

4.1　仿真说明

为了验证文中提出方法的有效性,仿真采用经典的Asia网络,用爬山法进行结构学习。对于一些特定的参数,数据权衡项K(s)中φ取500,融合先验信息项默认采用基于熵的罚项函数。为简便起见,若不作说明,本文先验给出的形式为对Asia网中所有真实存在的边加一个相同先验概率。例如当说正确先验为pi=[0.1,0.8,0.1],则所有真实存在的边的概率一律设pi=[0.1,0.8,0.1],此时给出的先验信息如图5所示。

表3　IS-HC算法流程

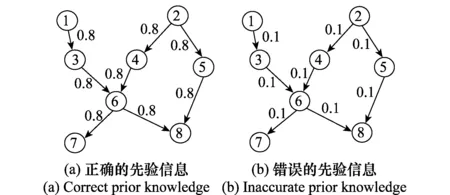
图5　仿真的先验信息

为证明本文提出算法的有效性,仿真过程中对不同数量的训练样本进行了对比测试。本文用贝叶斯信息准则(Bayesian information criterion,BIC)评分、Kullback-Leibler (KL)距离和汉明距离评判网络的优劣性。KL距离衡量学习得到的网络和真实网络分布的差距,而汉明距离是网络结构间的多边、少边、反边之和。评分越高、KL距离和汉明距离越小,说明学习得到的网络越接近真实网络。

4.2　本文方法有效性的验证

为验证本文的融合先验方法确实能够有效地利用先验信息,对用本文的方法融合正确先验和不融合正确先验进行对比仿真。先验设置为pi=[0.1,0.8,0.1],不同数据样本量的仿真结果如图6所示。

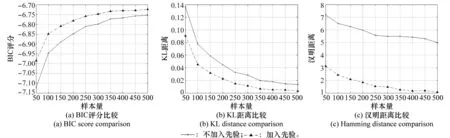
图6　两种方法在不同样本量下的比较

对图6进行分析,以BIC评分为例,添加先验的BIC评分明显高于无先验的BIC评分,KL距离和汉明距离的比较也有同样的结果,说明本文提出的方法能有效融合先验信息。

4.3　对错误先验适应能力分析

为验证本文提出几种方法对错误先验的适应能力,本节分别做以下仿真:有无数据权衡项的对比仿真,融合先验项中不同罚项函数的对比仿真,有无先验搜索算子的对比仿真。

4.3.1数据权衡项分析

为验证数据权衡项K(s)的效果,对不融合先验信息、融合错误先验信息无数据权衡项、融合错误先验信息有数据权衡项进行仿真,记录其结果进行对比。其中，错误先验信息设置为pi=[0.9,0.05,0.05],正确先验信息设置为pi=[0.1,0.8,0.1],不同数据样本量的仿真结果如图7所示。

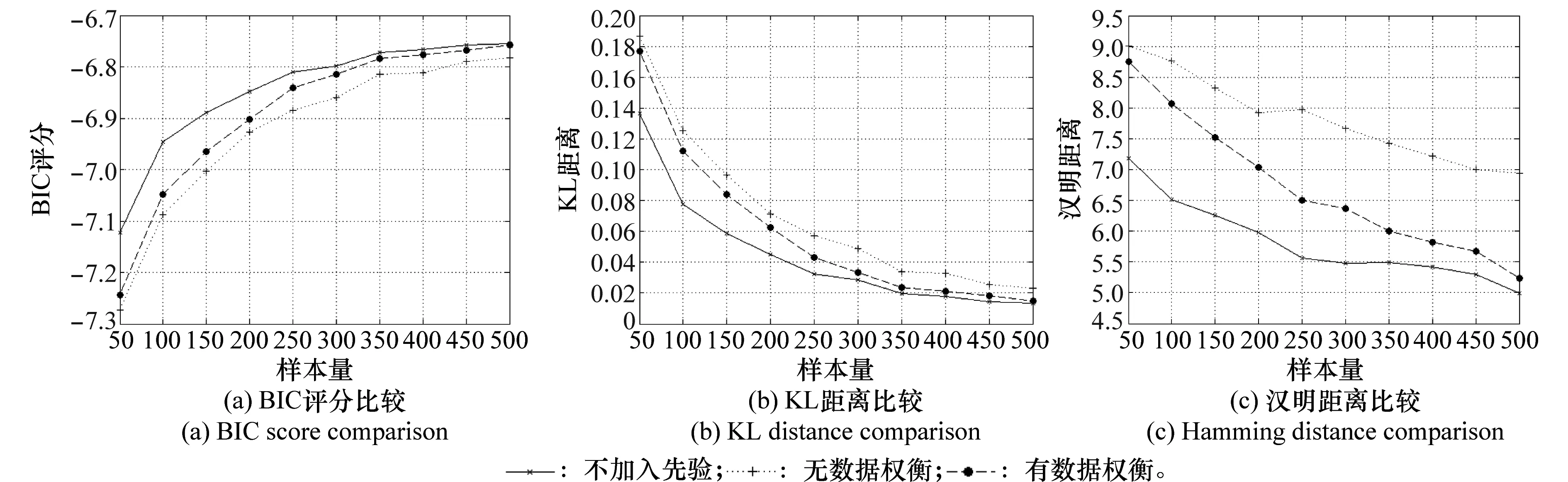
图7　有无数据权衡项的比较

对图7进行分析,以BIC评分为例,当样本量较小时,无权衡项和有权衡项方法的BIC评分类似,都明显低于不融合错误先验信息的BIC评分,但随着样本量增加,权衡因子发挥作用,有权衡项方法的得分曲线最后能逼近不融合错误先验信息的得分曲线,而无数据权衡的BIC评分始终比较小。KL距离和汉明距离的比较也有同样结果,说明了数据权衡项的有效性。

4.3.2融合先验信息项分析

为验证本文融合先验信息项中罚项函数构造的合理性,采取不同的错误概率值,观察学习结果的变化情况。错误概率设置为:pi=[(1-p)/2,p,(1-p)/2],图8中的横坐标值为p,仿真数据量取为200。文献[15]提出一种融合先验信息的贝叶斯网络结构学习方法,仿真中将其与本文所提方法做比较,对比对错误先验信息的适应能力，结果如图8所示。

对图8进行分析,以BIC评分为例,在错误的先验信息条件下,罚项函数用熵函数构造要比用线性函数构造得分要高,说明了前者对错误先验信息具有更好的适应能力。

用本文的方法与文献[15]提出的方法进行对比,当先验信息错误程度比较大时,本文采用熵函数构造方法的得分较高,对比而言说明本文方法在错误适应能力方面有一定优势。

KL距离和汉明距离的比较也有同样的结果,说明了本文罚项函数构造方法的合理性与有效性。

4.3.3先验搜索算子分析

为验证先验搜索算子的有效性,本节在仿真中设置两组错误的先验概率:p1,p2=[0.8,0.1,0.1]。其余正确的先验信息为:pi=[0.1,0.8,0.1],对加先验搜索算子和不加先验搜索算子两种情况进行了仿真对比,不同数据样本量的仿真结果如图9所示。

图8　不同融合先验项的比较

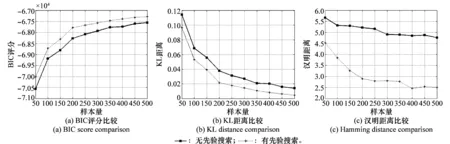
图9　有无先验搜索算子的比较

对图9进行分析,以BIC评分为例,应用先验信息搜索算子的方法得到的评分要更高,KL距离和汉明距离的比较也有同样的结果,说明在有部分错误先验信息的情况下,先验信息搜索算子能增强结构学习利用正确先验的鲁棒性,从而提高对错误先验信息的适应能力。

5　结　论

本文为了提高结构学习时对错误先验信息的适应能力,提出了一种新的融合先验信息进行结构学习的方法。仿真结果表明本文提出的方法能够有效地利用先验信息,并且对错误的先验信息有适应能力,降低错误先验信息带来的负面影响。另外,本文提出的模型高度概括了评分搜索法来利用先验信息的模式,参数可以自由调节,且可以应用到粒子群优化算法、遗传算法等方法中。下一步工作是进一步对融合先验信息的方法进行研究,以增强算法的容错性。

参考文献：

[1] SCHNEIDERMAN H. Object recognizer and detector for two-dimensional images using Bayesian network based classifier[P]. US: US 7848566 B2, 2015.

[2] HUANG J, YUAN Y. Construction and application of Bayesian network model for spatial data mining[C]∥Proc.of the IEEE International Conference on Control and Automation, 2007: 2802-2805.

[3] BANDYOPADHYAY S, WOLFSON J, VOCK D M, et al. Data mining for censored time-to-event data: a Bayesian network model for predicting cardiovascular risk from electronic health record data[J].Data Mining & Knowledge Discovery,2015,29(4): 1033-1069.

[4] SHENTON W, HART B T, CHAN T. Bayesian network models for environmental flow decision-making:1.Latrobe River Australia[J].River Research & Applications, 2015, 27(3): 283-296.

[5] CHICKERING D M. Learning Bayesian networks is NP-complete[J]. Networks, 1996, 112(2): 121-130.

[6] KOLLER D, FRIEDMAN N. Probabilistic graphical models[M]. Cambridge: MIT Press, 2009.

[7] 邸若海, 高晓光, 郭志高. 小数据集BN建模方法及其在威胁评估中的应用[J]. 电子学报, 2016, 44(6):1504-1511.

DI R H, GAO X G, GUO Z G. The modeling method with Bayesian networks and its application in the threat assessment under small data sets[J]. Acta Electronica Sinica, 2016, 44(6):1504-1511.

[8] AMIRKHANI H, RAHMATI M, LUCAS P, et al. Exploiting experts’ knowledge for structure learning of Bayesian networks[J]. IEEE Trans.on Pattern Analysis & Machine Intelligence, 2016, PP(99): 2154-2170.

[9] CANO A, MASEGOSA A R, MORAL S. A method for integrating expert knowledge when learning Bayesian networks from data[J]. IEEE Trans.on Systems, Man & Cybernetics-Part B: Cybernetics, 2011, 41(5): 1382-1394.

[10] ANGELOPOULOS N, CUSSENS J. Bayesian learning of Bayesian networks with informative priors[J]. Kluwer Academic Publishers,2008,54(1/3):53-98.

[11] COOPER G F, HERSKOVITS E. A Bayesian method for the induction of probabilistic networks from data[J]. Machine Learning, 1992, 9(4): 309-347.

[12] CAMPOS L M D, CASTELLANOA J G. Bayesian network learning algorithms using structural restrictions[J]. International Journal of Approximate Reasoning,2007,45(2):233-254.

[13] CASTELO R, SIEBES A. Priors on network structures. Biasing the search for Bayesian networks[J]. International Journal of Approximate Reasoning, 2000, 24(1): 39-57.

[14] HECKERMAN D, DAN G, CHICKERING D M. Learning Bayesian networks: the combination of knowledge and statistical data[J]. Machine Learning, 1995, 20(3): 197-243.

[15] BORBOUDAKIS G, TSAMARDINOS I. Scoring and searching over Bayesian networks with causal and associative priors[C]∥Proc.of the 29th International Conference on Uncertainty in Artificial Intelligence, 2013: 1210-1232.