联合互协方差矩阵的快速波达方向估计

闫锋刚, 荣加加, 刘　帅, 沈　毅, 金　铭

(1. 哈尔滨工业大学(威海)信息与电气工程学院, 山东 威海 264209; 2. 哈尔滨工业大学电子与信息工程学院, 黑龙江 哈尔滨 150001)

0　引　言

波达方向(direction-of-arrival, DOA)估计是阵列信号处理的一个重要研究方向,其在雷达[1]、通信[2]、声呐[3]、地震[4]和天文[5]等科技领域得到广泛应用。以多重信号分类(multiple signal classification, MUSIC)[6-9]和旋转不变子空间[10-11]为代表的子空间类估计算法的提出,实现了传统DOA估计向超分辨DOA估计的跨越式发展。子空间类算法的关键在于通过对阵列协方差矩阵进行奇异值分解(singular value decomposition, SVD)或特征值分解(eigenvalue decomposition, EVD)来获得噪声子空间或信号子空间。通常,矩阵EVD和SVD运算都涉及庞大的计算量,尤其是在阵列阵元数多的情况下这种劣势更加明显,这也阻碍了子空间类算法的工程化进度。

为克服子空间类算法计算量大的问题,中外学者提出了众多性能可靠的替代性算法。文献[12]提出一种传播因子算法(propagator method, PM),通过协方差矩阵的线性运算来构造噪声子空间,有效避开了对协方差矩阵的EVD或SVD运算;文献[13]则利用协方差矩阵的任意K(K为信号源数目)行来求得一个低维的投影矩阵,并在此基础上构造一个低维搜索函数来实现角度估计;文献[14-16]提出一种多级维纳滤波(multistage Wiener filtering,MSWF)算法,该方法通过正交投影来获取子空间,同样避开了计算量较大的EVD运算,实现了算法计算量的降低,但该方法获得的子空间精度不是太高。

文献[17]提出一种基于L型阵列的快速2维高效子空间算法(computationally efficient subspace algorithm, CESA)。该算法分别利用协方差矩阵的第1行、第1列和主对角线元素构造出用于求解方位角、俯仰角和角度配对的3个向量,并通过重组这3个向量的元素,最终构造出等价的信号子空间[18]。虽然CESA算法是基于L阵提出的2维DOA估计,但该算法中的L阵的每个轴都由均匀线阵(uniform linear array, ULA)构成,因此其同样适用于基于ULA的1维DOA估计。本文基于CESA的基本思想,提出一种新的基于ULA的JCCM估计算法,所提算法在阵列模型上将完整的ULA均匀划分成2个子阵,然后求取2个子阵的前向和后向互协方差矩阵,再利用这些信息经过简单的线性运算重构出替代的信号子空间,从而构造多项式并求根估计出角度。本文最后用若干个实验仿真来验证算法的有效性、估计精度和估计速度等性能。

1　阵列结构及数据模型

设K个不相干的窄带远场信号s1(t),s2(t),…,sK(t)分别以角度θ1,θ2,…,θK入射到xoy平面内由2N个各向同性且均匀分布的阵元所构成的ULA上,如图1所示。定义DOA为信号来向与阵列法线的夹角。假设阵列各通道噪声为加性高斯白噪声,且各通道噪声相互独立并与信号不相关。现将阵列划分成阵元数目均为N的两组,分别记为子阵a和子阵b,以第1个阵元为参考阵元,则两个子阵t时刻的接收数据矢量可分别表示为

A(θ)s(t)+na(t)

(1)

A(θ)Φs(t)+nb(t)

(2)

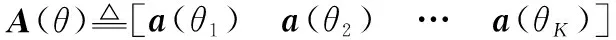
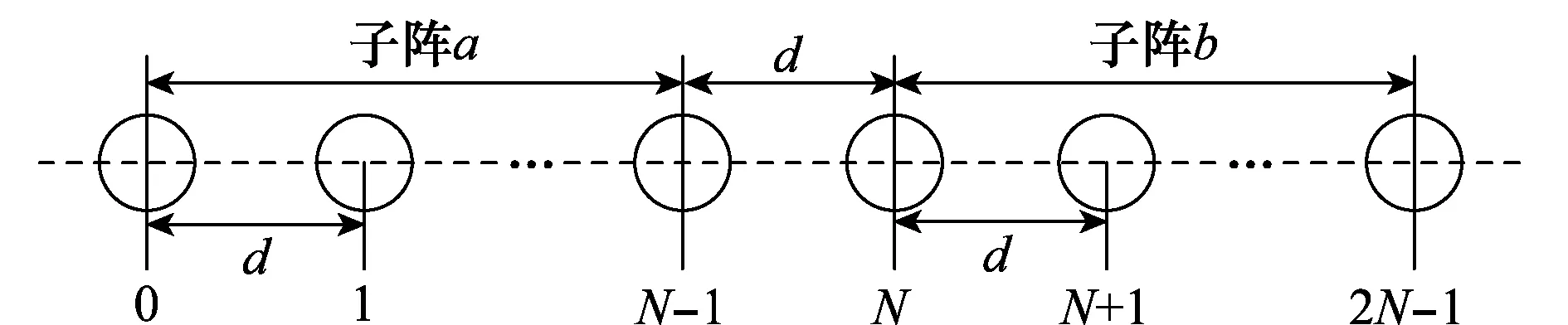
图1　ULA模型

2　联合互协方差矩阵的DOA估计

2.1　算法原理

为抑制加性噪声的干扰,定义矩阵Rab为子阵a数据与子阵b数据的互协方差,称为前向互协方差,矩阵Rba为子阵b数据与子阵a数据的互协方差,称为后向互协方差。根据式(1)和式(2),有

(3)

(4)

式中,RsE{s(t)sH(t)}表示入射信号的自协方差矩阵。因为噪声矢量na(t)与nb(t)是统计独立的关系,所以有基于信号si(t)(i=1,2,…,K)互不相关的假设,信号的自协方差矩阵RS是对角阵,且对角线元素与信号能量一一对应,即

(5)

式中,pi(i=1,2,…,K)表示第i个信号的能量。

利用前向互协方差矩阵和后向互协方差矩阵构造联合互协方差矩阵(joint cross-covariance matrix,JCCM),记为RJCCM,具体表示为

RJCCMRab+Rba=A(θ)RSΦHAH(θ)+A(θ)ΦRSAH(θ)=

A(θ)(RSΦH+ΦRS)AH(θ)=A(θ)ΛAH(θ)

(6)

式中,ΛRSΦH+ΦRS。

由于Rs和Φ均为对角阵,因此矩阵Λ也为对角阵,且可进一步表示为

Λ=RSΦH+ΦRS=

RSΦH+RSΦ=RS(ΦH+Φ)=

(7)

式中,ξipi(ejNαi+e-jNαi)(i=1,2,…,K)。因为信号能量pi为正实数,所以ξi也为正实数,进一步有Λ=Λ*。

(8)

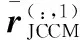
JNA*(θ)Λ1

(9)

(10)

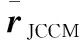
(11)

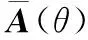
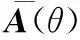
(12)

G=CΛD

(13)

式中,C是(2N-K)×K维矩阵;D是K×K维矩阵,且

(15)

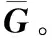
(16)

式中

(17)

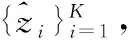
(18)

实际应用中,协方差矩阵的计算公式为

(19)

所以式(3)、式(4)的实现公式为

(20)

(21)

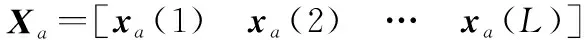
(22)

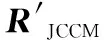
(23)

(24)

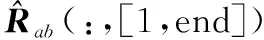
(25)

(26)

2.2　算法实现步骤描述

综上所述,本文的JCCM算法具体实现步骤如下:

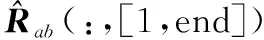
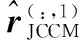
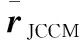
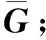
步骤6由式(16)构造求根多项式fJCCM(z),求其K个最接近于单位圆的根,由式(18)求得信号入射方向。

从上述步骤可见,本文提出的JCCM算法利用子阵划分和矩阵重构思想,通过对低维(N×1维)联合互协方差矩阵RJCCM进行线性操作得到等效的高维((2N-K)×K维)信号子空间,避免了直接对全阵列2N×1维协方差矩阵进行EVD或SVD操作,实现了计算量的简化。

2.3　算法复杂度分析

对阵元数为2N的均匀线阵分别运用本文的JCCM算法和root-MUSIC算法进行DOA估计,设快拍数为L,入射信号源数目为K。

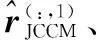
常规root-MUSIC算法的计算量主要在于协方差矩阵计算、特征值分解和多项式求根,这3步操作的计算量分别为O(4N2L)、O(8N3)和O(8(2N-1)3),所以root-MUSIC算法总的计算量为O(4N2L+8N3+8(2N-1)3)。

由于通常情况下快拍数L、阵元数N及信号源数K满足L≫N>K,所以JCCM算法相对于root-MUSIC算法计算量显著降低。

3　仿真实验及分析

进行仿真实验以验证本文提出的JCCM算法的性能。仿真中,阵列结构采用图1所示ULA模型,总阵元数2N=16,即各子阵包含8个阵元,入射信号源数K=2,入射角度分别为θ1=-15°,θ2=0°,阵元间距为半波长。实验还作出了root-MUSIC算法及CESA算法的性能曲线作为参考。

实验1DOA估计的有效性仿真

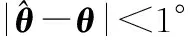
实验条件:快拍数固定为500,信噪比(signal-to-noise ratio,SNR)由-5 dB增加到10 dB。蒙特卡罗实验次数为100次。仿真得出的成功概率与SNR的关系如图2所示。

图2表明,在SNR由-5 dB增加到10 dB的过程中,JCCM与root-MUSIC的成功概率相近,而CESA的成功概率始终不如JCCM及root-MUSIC。说明本文的JCCM算法提高了算法的稳定性。

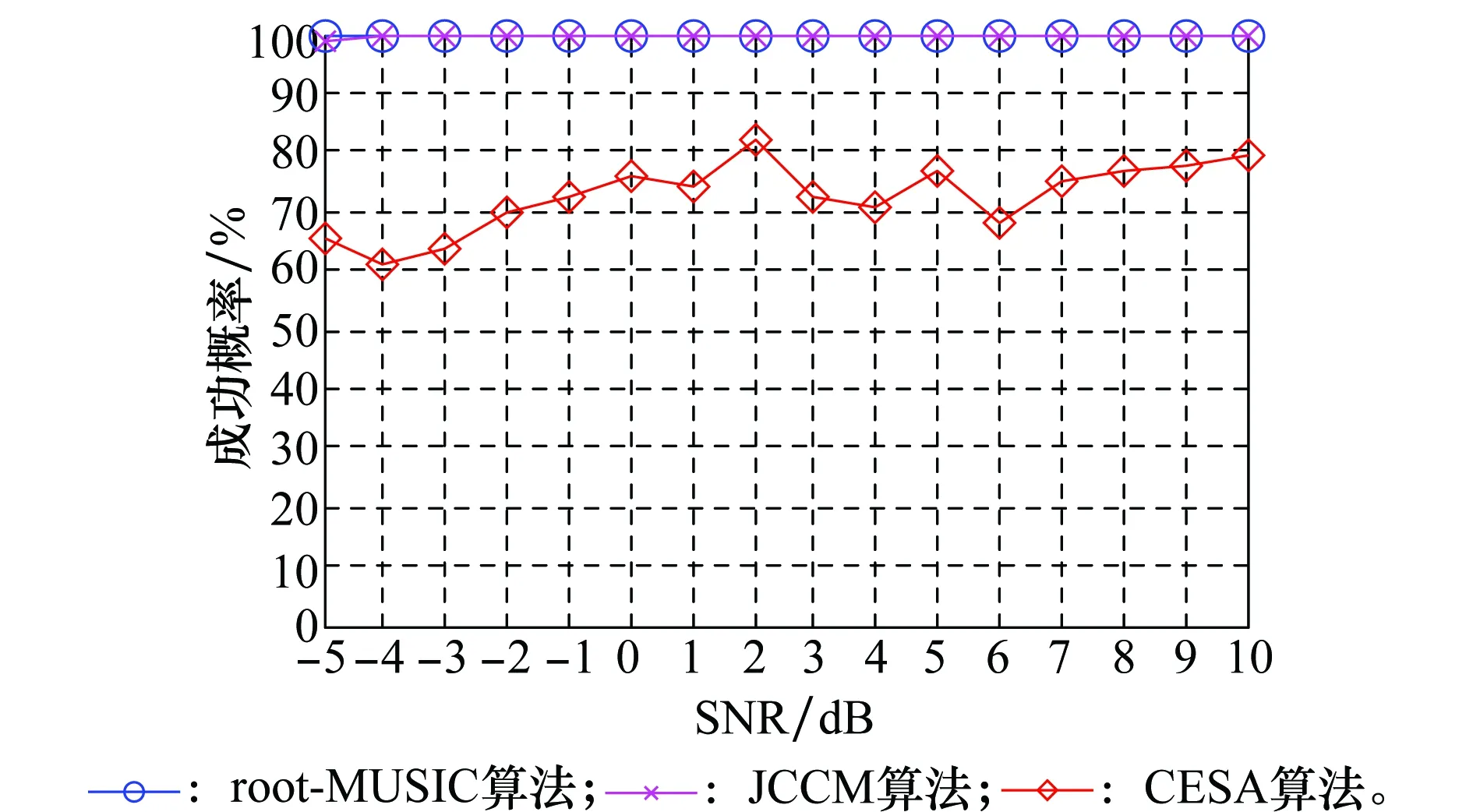
图2　成功概率与SNR的关系

实验2均方根误差的仿真

算法的均方根误差(root-mean-square error, RMSE)随SNR和快拍数的变化情况可用来反映不同情况下的算法估计精度。定义RMSE为

(27)

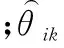
(1) RMSE随SNR的变化

仿真条件:快拍数固定为500,SNR由0 dB增加到15 dB。蒙特卡罗实验次数为500次。仿真结果如图3所示,其中图3(a)为3种算法共同比较的结果,为突出显示JCCM与root-MUSIC的曲线差异,图3(b)给出了JCCM与root-MUSIC单独比较的结果。

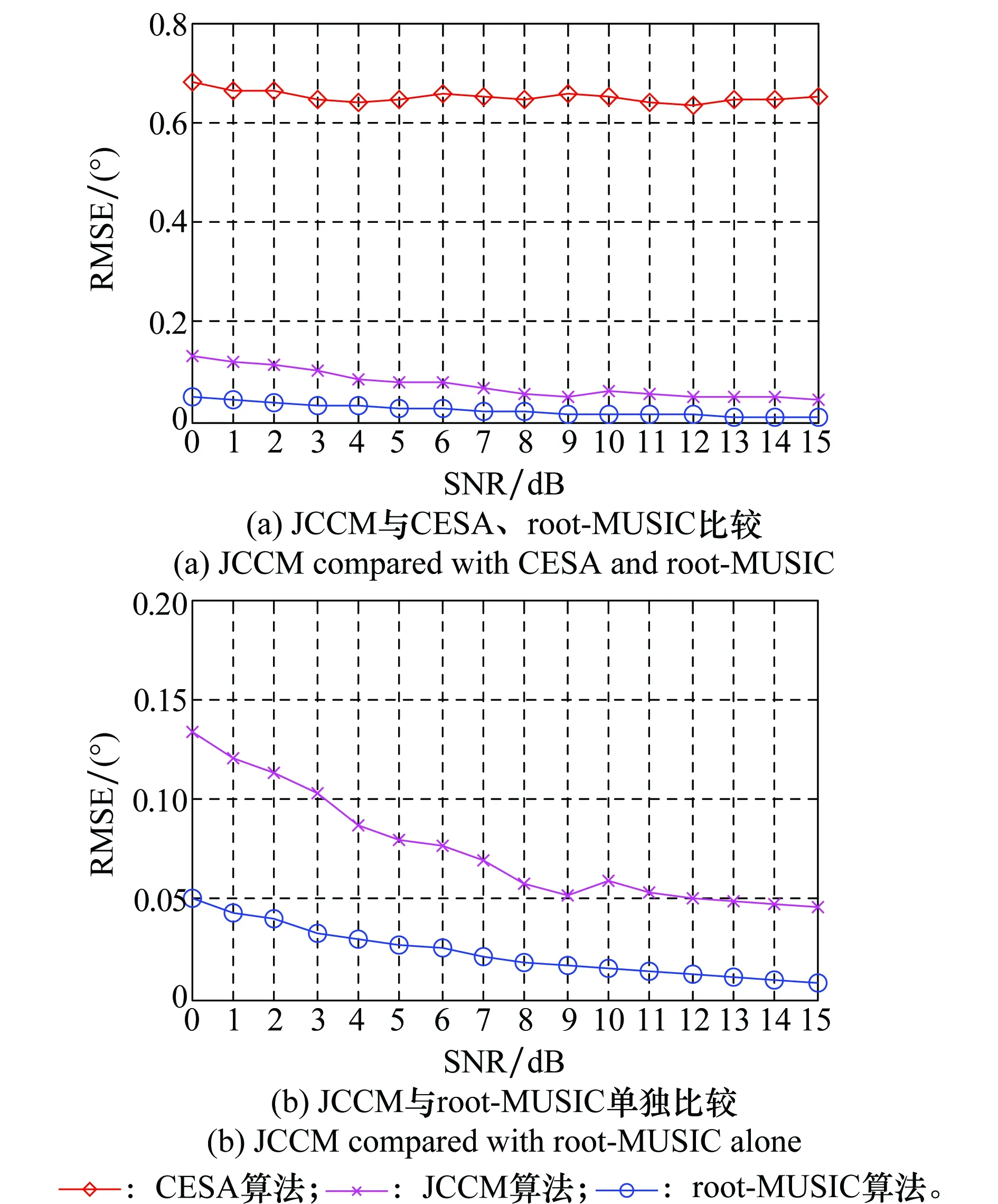
图3　RMSE与SNR的关系

由图3可以看出,在整个SNR变化范围内,JCCM的RMSE明显低于CESA,但是始终高于root-MUSIC。从理论的角度分析,JCCM的估计精度高于CESA主要得益于JCCM算法同时利用了前向、后向互协方差,而CESA算法只求解了前向互协方差;然而,JCCM只取联合互协方差矩阵的第1列构造信号子空间,相对于root-MUSIC利用了整个协方差矩阵获取子空间而言,还是丢失了一定的有用信息,所以估计精度也相应降低。事实上,从图3(b)可以看出,当SNR大于3 dB时,JCCM算法可以达到RMSE低于0.1°的估计精度,这样的估计精度在多数工程应用中是可被接受的。

(2) RMSE随快拍数的变化

仿真条件:信噪比固定为10 dB,快拍数从100增加到1 000。蒙特卡罗实验次数为500次。仿真结果如图4所示,其中图4(a)为3种算法共同比较的结果,与图3(b)同理,图4(b)给出了JCCM与root-MUSIC单独比较的结果。

图4　RMSE与快拍数的关系

图4反映的RMSE随快拍数变化的趋势与图3反映的变化趋势基本一致,即在整个快拍数变化范围内,JCCM算法的RMSE介于CESA和root-MUSIC之间,且要明显低于CESA,虽然高于root-MUSIC,但在快拍数大于200时便已小于0.1°,同样已经可以达到多数工程应用的精度要求了。

实验3角度估计的速度仿真

角度估计速度使用算法在不同快拍数下的单次估计时间来衡量。实验中取蒙特卡罗实验运行时间的平均值作为算法的单次估计时间。

仿真条件:SNR固定为10 dB,快拍数由100变化到2 000,蒙特卡罗实验次数为500。估计时间与快拍数关系的仿真结果如图5所示。

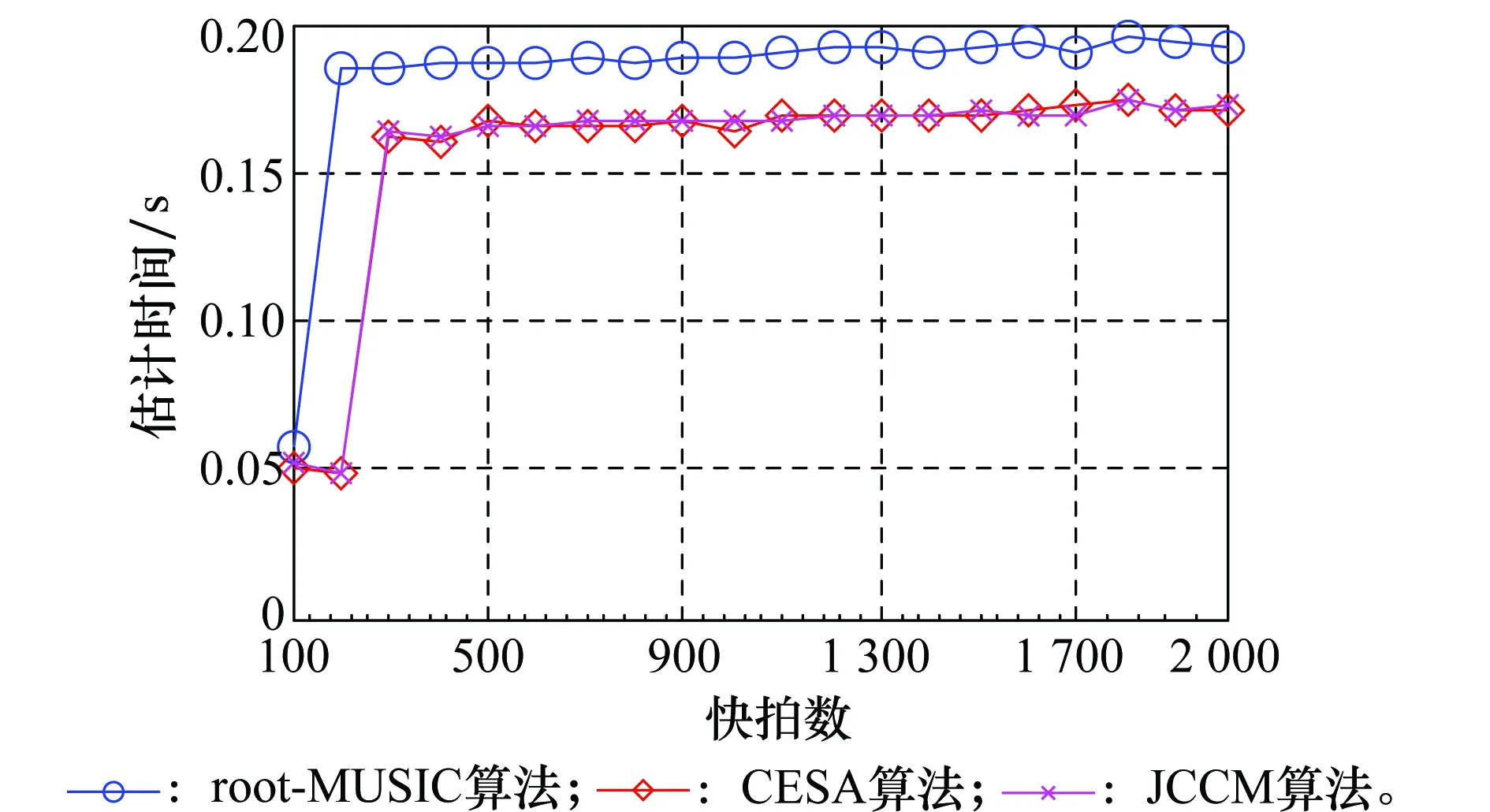
图5　估计时间与快拍数的关系

由图5可以看出,在整个快拍数变化范围内,JCCM与CESA算法的单次平均估计时间始终小于root-MUSIC算法,仿真结果验证了算法估计速度上的优势。需要说明的是,图5显示出小快拍数下估计时间明显小于大快拍数下的估计时间,从理论角度分析,这是由于快拍数较小时求得的协方差矩阵并不满秩,从而特征值分解运算量小且求根多项式阶次低,所以总体运算量较小。当快拍数较大时,协方差矩阵近似为满秩,此时特征值分解运算量及求根多项式的阶次均与阵元数成正比,而不受快拍数影响,快拍数仅影响求解协方差矩阵的运算量,因此3种算法随快拍数变化的趋势相一致。

4　结　论

本文提出一种基于ULA的联合互协方差矩阵的DOA估计算法。算法避开繁琐的子空间分解过程,利用子阵接收数据的前向和后向互协方差矩阵构造了联合互协方差矩阵,并利用其重构出了等价的信号子空间,最后构造多项式通过求根实现了入射角度的估计。结果表明,本文的JCCM算法在保证估计精度可接受的同时,有效降低了计算量,实现了估计速度的提高。

参考文献：

[1] WANG X, WANG L, LI X, et al. An efficient sparse representation algorithm for DOA estimation in MIMO radar system[C]∥Proc.of the IEEE International Workshop on Signal Processing Advances in Wireless Communications, 2016:1-4.

[2] LIU L, LIU H. Joint estimation of DOA and TDOA of multiple reflections in mobile communications[J]. IEEE Access, 2016, 4:3815-3823.

[3] SAUCAN A A, CHONAVEL T, SINTES C, et al. CPHD-DOA tracking of multiple extended sonar targets in impulsive environments[J].IEEE Trans.on Signal Processing,2016,64(5):1147-1160.

[4] YAN G, LI G, NING L. Method on fast DOA estimation of moving nodes in ad-hoc network[C]∥Proc.of the IEEE International Symposium on Communications and Information Technology, 2006:1169-1172.

[5] LEVANDA R, LESHEM A. Adaptive selective sidelobe canceller beamformer with applications to interference mitigation in radio astronomy[J].IEEE Trans.on Signal Processing,2013, 61(20):5063-5074.

[6] SANTOSH S, SHARMA K. A review on multiple emitter location and signal parameter estimation[J]. International Journal of Engineering Research, 2013, 2(3):276-280.

[7] YAN F G, JIN M, LIU S, et al. Real-valued music for efficient direction estimation with arbitrary array geometries[J]. IEEE Trans.on Signal Processing, 2014, 62(6):1548-1560.

[8] BASIKOLO T, ARAI H. APRD-MUSIC algorithm DOA estimation for reactance based uniform circular array[J]. IEEE Trans.on Antennas & Propagation,2016,64(10):4415-4422.

[9] 闫锋刚,张薇,金铭.求根MUSIC初值设置和更新算法[J].哈尔滨工业大学学报,2015, 47(3): 88-92.

YAN F G, ZHANG W, JIN M. A new method for setting and updating the initiation of root-MUSIC[J]. Journal of Harbin Institute of Technology, 2015, 47(3): 88-92.

[10] ROY R, PAULRAJ A, KAILATH T. ESPRIT: a subspace rotation approach to estimation of parameters of cissoids in noise[J]. IEEE Trans.on Acoustics,Speech,and Signal Processing，1986, 34(5): 1340-1342.

[11] LIN J, MA X, YAN S, et al. Time-frequency multi-invariance ESPRIT for DOA estimation[J]. IEEE Antennas & Wireless Propagation Letters, 2016, 15(1):770-773.

[12] MARCOS S, MARSAL A, BENIDIR M. Performances analysis of the propagator method for source bearing estimation[C]∥Proc.of the IEEE International Conference on Acoustics, Speech, & Signal Processing,1994:237-240.

[13] YEH C C. Simple computation of projection matrix for bearing estimations[J]. IEE Proceedings F-Communications, Radar and Signal Processing, 1987, 134(2):146-150.

[14] GOLDSTEIN J S, REED I S, SCHARF L L. A multistage representation of the Wiener filter based on orthogonal projections[J].IEEE Trans.on Information Theory, 1998, 44(7):2943-2959.

[15] HUANG L, WU S, FENG D, et al. Low complexity method for signal subspace fitting[J]. Electronics Letters, 2004, 40(14): 847-848.

[16] HUANG L, WU S. Low-complexity MDL method for accurate source enumeration[J]. IEEE Signal Processing Letters, 2007, 14(9): 581-584.

[17] XI N, LI L. A computationally efficient subspace algorithm for 2-D DOA estimation with l-shaped array[J]. IEEE Signal Processing Letters, 2014, 21(8):971-974.

[18] 荣加加.特殊阵列下的快速波达方向估计[D].哈尔滨：哈尔滨工业大学,2017:19-32.

RONG J J. Fast direction of arrival estimation based on special array configurations[D].Harbin:Harbin Institute of Technology, 2017:19-32.