槽形主梁非对称式独塔斜拉桥车桥耦合分析

杨著，郭向荣，唐俊锋，朱志辉

(1. 中南大学 土木工程学院，湖南 长沙 410075；2. 上海市政工程设计研究总院(集团)有限公司，上海 200092)

近年来，随着分析理论和电算技术的进步，斜拉桥的发展十分迅速，其中独塔斜拉桥由于其具有造型优美、经济适用和力学性能良好等优点，在斜拉桥的建设中得到日益广泛的应用[1−3]，特别是在跨径400 m以下的桥梁中。混凝土槽形梁是一种下承式板梁组合结构[4]，由位于两侧的主梁、中间的道床板组成，当铁路桥梁采用槽形梁主梁时，轨道设施等结构置于中间道床板上，节约高度空间，槽形结构可在一定程度上减少列车行驶时轮轨摩擦产生的噪声[5−6]，能阻止车辆出轨及倾覆下落。此外，槽形梁的结构高度主要与其横向宽度有关，与其纵向跨度关系不大，故在纵向大跨度条件下其优势更明显。目前，将槽形梁作为中小跨度桥梁上部结构的一种形式在国内外已有较多应用[7−8]，把槽形梁应用于大跨度桥梁的案例则少见，而研究也多集中于中小跨度桥梁。田杨等[7]对某铁路曲线简支槽形梁桥展开空间分析，研究结果表明，在竖向荷载作用下，槽形梁的受力呈现明显的空间特性，道床板的剪力滞现象比较显著等结论；吴亮秦等[8]对某薄壁槽形梁展开车桥动力特性试验研究，结果表明该槽形梁具有足够的刚度，动力性能良好，并指出应当重视道床板和腹板的局部稳定性。在设计独塔斜拉桥时采用槽形主梁方案则能将这2种结构形式的特点结合起来，充分发挥两者的优势，因而具有良好的工程应用前景。对此种桥梁系统的静力性能展开研究日益增多，戴公连等[9]对槽形梁斜拉桥的塔梁固结区域的受力特点展开研究，朱志辉则对槽形梁斜拉桥不同卸索工况下列车−轨道−桥梁耦合系统振动响应进行了研究[10]。但总体而言，目前对这种结构的动力性能及列车于其上行驶时的走行性的研究仍较少。

本文以某主跨112 m的非对称式独塔斜拉桥为研究对象，建立全桥有限元分析模型，采用薄壁槽形梁段单元方法模拟主梁，在适当简化后，CRH2客车的每节车辆(含机车)考虑23个空间自由度，建立并采用逐步积分法求解耦合系统的振动方程，得到桥梁关键节点的动力响应和车辆响应，对列车行车安全性及舒适性是否满足要求进行分析判断，并从动力学角度对非对称式独塔斜拉桥采用槽形主梁的可行性进行探讨。

1　工程背景

本文的研究背景为某主跨为112 m的独塔非对称式混凝土斜拉桥，桥梁跨径布置为(112+80+32)m，右侧边跨设置一辅助墩，其总体布置如图1所示。该斜拉桥与桥下公路交叉，斜交角度为 69°，为不影响公路的正常运营，采用转体法施工。斜拉索采用空间双索面体系，主塔两侧各有8对，呈扇形不对称布置。桥梁的设计速度为120 km/h，单线行车。

图1　桥梁结构总体布置图Fig. 1　Overall arrangement of bridge structure

图2　主梁截面图Fig. 2　Main girder cross-section

斜拉桥主梁由混凝土浇筑而成，采用箱形腹板槽形截面，具体构造如图2所示。箱形腹板的优点是截面抗扭刚度较大，纵向预应力钢束及斜拉索均可于箱内锚固，避免开槽或设锯齿块。主梁混凝土等级C50。槽形梁梁宽10.8 m，槽内净宽6.9 m。主梁箱形截面顶宽 2.1 m，在支点处设进人孔。主跨截面高度为3.8 m，腹板厚度0.3 m，道床板厚度0.45 m；边跨截面高度为4.0 m，腹板厚度0.55 m，道床板厚度0.65 m；主塔支点及端支点处主梁截面高度为4.3 m，腹板厚度为0.55 m，道床板厚度0.95 m。道床板顶设2%的双向排水坡。桥塔采用空心截面，混凝土等级C50，索塔采用钻石型桥塔，桥面以上塔高49.5 m。塔柱为单箱单室截面，顺桥向宽6.0 m，横桥向宽4.4 m，纵向壁厚0.8 m，横向壁厚0.7 m；分叉之后顺桥向宽6.0 m，横桥向宽3.0 m，纵向壁厚0.8 m，横向壁厚0.6 m。边墩及辅助墩均为实心截面，混凝土等级C40。

2　车−桥耦合振动分析模型

2.1　桥梁模型

斜拉桥采用空间薄壁的槽形主梁，与普通闭口箱梁的力学特点相比有较大不同，如用空间梁单元来离散模拟，则不能考虑到槽形梁具有的横向弯扭耦合振动和约束扭转变形等力学特点[11−12]，计算结果误差会较大。如采用实体单元对槽形梁进行离散建模，则单元数太多，计算量大，在保障计算精度的情况下，根据槽形梁构造特点建议采用槽形薄壁梁段有限元法来模拟，该方法的基本思路是将斜拉桥的槽形主梁沿桥梁跨长划分为若干个梁段单元[12]，其横截面如图3所示。图3中位于下部的S点为扭转中心，C点为形心，坐标系原点则取在形心点C处。根据符拉索夫理论，槽形梁在受力变形过程中，其横截面的形状应始终不变，则横截面的位移应包含沿x轴的横向位移u，沿y轴的竖向位移v，沿z轴的纵向位移w和绕扭转中心S的扭转角φ。每个梁段单元有2个节点，每个节点有7个自由度：iu，iu′，iv，iv′，iw，iφ和iφ′。在确定形函数时，纵向位移形函数取一次多项式，而考虑到槽形截面的约束扭转变形，结点位移应当包含扭转角φ沿单元长度的变化率，故单元的横向水平和竖向位移、扭转角的形函数均采用三次Hermite多项式。单元节点的横向、竖向、纵向和扭转位移列

图3　槽型梁横截面尺寸示意图Fig. 3　Channel beam cross-section

建立桥梁其他部位计算模型时，按其不同结构部位的力学特点采用相应的单元。如混凝土主塔、桥墩及其以下部分均采用空间梁单元模拟，斜拉索则采用空间杆单元进行模拟。所有构件的弹性模量E和泊松比μ按现行铁路桥梁规范取值，铁路桥面二恒取67.9 kN/m。该模型采用塔、梁互为固结的体系，故桥塔与主梁采用主从约束的形式刚接，主梁与边墩则放松纵向的水平平动自由度。图4为其空间有限元分析模型。

图4　桥梁有限元分析模型Fig. 4　Finite element analysis model of bridge

2.2　列车模型

高速列车的结构十分复杂，难以对车辆各部件的振动状态进行精确的模拟，故在建立车辆动力分析模型时，通常根据需要会对车辆模型进行若干的假定与简化。按照文献[13]假定，车体在作空间振动时，应当考虑横向(侧摆)、侧滚、摇头、点头、垂向(浮沉)等 5个方向的自由度，同样每个构架也考虑类似5个自由度，而每个轮对仅考虑横向，垂向2个自由度。客车车辆由1个车体、2个构架及4个轮对等7刚体组成，计算可得每台四轴车辆共有23个自由度，具体可见表1，客车车辆及机车均按二系弹簧计算。

由车辆动力学理论，可得到车辆的运动方程如下：

表1　车辆模型的自由度表Table 1　Degrees of freedom of vehicle model

2.3　列车−桥梁耦合振动方程的建立及求解

本文将桥上通行列车与斜拉桥视为整体耦合振动系统。考虑列车车辆和桥梁空间振动位移的相互关系，计算任意时刻t时的桥上列车及桥梁空间振动的弹性总势能。根据势能驻值原理[13−14]和形成矩阵的“对号入座”方法，建立t时刻此系统的振动矩阵方程如下：

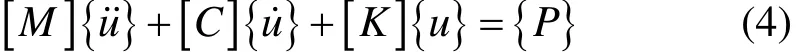
式中：[M]，[C]和[K]分别为质量、阻尼和刚度矩阵，{u}，{}u˙和{}u˙则分别为车辆、桥梁耦合动力系统在t时刻的位移、速度以及加速度参数列阵。将车辆轴重、轨道竖向不平顺函数和构架蛇形波函数代入方程(4)中，并采用Wilson-θ法逐步积分求解。可解出此耦合动力系统的空间振动响应。

2.4　列车安全、舒适及平稳性运行指标及桥梁动力响应限值

脱轨系数为在某时刻作用于列车车轮上的横向力Q与垂向力P之比值。本文根据中国《高速铁路设计规范(试行)》中，采用0.8的限值。评定列车运行安全性的另一个重要指标是轮重减载率，目前各国采用的轮重减载率的限值也有所不同，我国在规范《铁道车辆动力学性能评定和试验鉴定规范》(GB5599—85)中，轮重减载率的允许限度的控制值是 0.6，危险限度控制值为 0.65。参考相关铁路规范，本文采用桥梁横向振动加速度限值为 0.14g(g为重力加速度)，桥梁竖向振动加速度限值为 0.35 g，我国列车运行的平稳性指标采用Sperling指标，具体值见表2。

表2　车辆平稳性评定标准Table 2　Stability evaluation standard of locomotive and vehicle

3　计算结果分析

3.1　桥梁自振特性分析

桥梁的自振特性是桥梁动力性能直接的体现，是进行车桥耦合振动分析的基础。采用前面建立的桥梁有限元计算模型，用子空间迭代法对该独塔斜拉桥的自振特性进行了计算分析。前 10阶自振频率计算值及振型特点总结于表3，绘出前3阶振型图见图5~7。

表3　桥梁振型及频率Table 3　Vibration modes and frequencies of the bridge

由图5~7可见，该独塔斜拉桥振动具有明显的空间特性，各向振动耦合性较强，振型有以下特点：

1) 桥梁的第1阶自振频率为0.836 Hz，周期约为1.2 s，小于5 s，属于短周期范畴。振型为塔梁横弯，说明桥梁横向抗弯刚度比竖向抗弯刚度要小，另外，主塔左侧主梁的横弯幅度要大于右侧，这是由于桥梁主塔左边的跨度大于右边即桥梁结构本身不对称造成。

2) 桥梁的第2和第3阶振型为主梁竖弯并伴随主塔面内侧倾，侧倾是由于主梁和主塔通过斜拉索连接影响而造成，桥梁模型整体性较强。

3) 前10阶振型中第4，7和8阶均出现主梁扭转振型且与墩梁横弯耦合。说明槽形梁作为开口截面其抗扭转的能力较弱，斜拉索及结构体系使桥梁的侧向弯曲和扭转强烈地耦合，这也说明采用槽形梁段单元方法来模拟槽形主梁能很好地体现其力学特点。

图5　第1阶振型图(俯视图)Fig. 5　1st vibration mode (Vertical view)

图6　第2阶振型图(正视图)Fig. 6　2nd vibration mode (Front view)

图7　第3阶振型图(俯视图)Fig. 7　3rd vibration mode (Vertical view)

3.2　桥梁动力响应结果及其分析

根据前述计算原理与车桥模型，采用自编车桥耦合动力计算软件TBI(Train-Bridge-Interaction)，建立斜拉桥的全桥分析模型。进行车桥耦合振动计算分析时，选用国产CRH2列车，编组为(动+拖+拖+动)*2，两列联挂，单线行车，计算速度为 80~160 km/h。计算结果主要输出包括斜拉桥的竖向与横向动位移、车辆竖向与横向加速度、轮对最大横向力、轮对脱轨系数、轮重减载率等关键数据。计算中轨道不平顺函数采用了德国低干扰谱。

表4给出了CRH2列车以80~160 km/h单线通过时桥梁响应的最大值，表中振动位移值均为相对于初始平衡位置而言。

分别绘出了CRH2列车以120 km/h单线通过桥梁时引起的横、竖向位移及加速度时程曲线。图 8为主跨跨中横向位移、加速度时程曲线；图9为主跨跨中竖向位移、加速度时程曲线；图 10为塔顶纵向位移、加速度时程曲线。

从表4看出，桥梁112 m主跨跨中横向最大动位移为 0.12 mm，80 m中跨跨中横向最大位移为0.06 mm，横向位移值和横向挠跨比都很小，说明列车在过桥时对桥梁横向振动影响较小，桥梁横向刚度足够。主跨跨中竖向最大动扰度为15.35 mm，大约为主跨跨径的1/7 300，根据前节表2的限值要求可以看出，桥梁的动力响应均在容许值以内。墩顶横向最大位移为0.15 mm，塔顶纵向位移最大值为6.58 mm，位移值均较小。

表4　桥梁动力响应最大值Table 4　Maximum dynamic response of bridges

图8　主跨跨中横向位移(左)、加速度(右)时程曲线(120 km/h)Fig. 8　Time history of lateral displacement(left)、acceleration(right) curve at the main-span(120 km/h)

由图8可见，当列车以120 km/h单线通过桥梁时，主跨跨中横向位移数值不大，但其时程曲线摆动明显。由图9可见，与主跨跨中横向位移时程曲线形式不同，随着列车上桥，主跨跨中竖向位移快速增大，在约3 s时达到峰值，然后逐渐减少，在6 s后，随着列车逐步驶离桥梁，其竖向动位移快速减少，在列车出桥时刻归于0。图8和图9中加速度时程曲线大致呈两头尖细的纺锥形，符合一般规律。从图 10可见，列车上桥开始，桥塔塔顶纵向位移开始快速增大，在大约3s时，列车行驶到主跨跨中，此时塔顶纵向位移达到最大值，其后再减小，在9 s时，塔顶位移为反方向最大值，此后随列车驶出桥梁，塔顶纵向动位移归于0。

图9　主跨跨中竖向位移(左)、加速度(右)时程曲线(120 km/h)Fig. 9　Time history of vertical displacement (left), acceleration (right) curve at the main-span (120 km/h)

图10　塔顶纵向位移(左)、加速度(右)时程曲线(120 km/h)Fig. 10　Time history of longitudinal displacement (left)、acceleration (right) curve at the top of the tower (120 km/h)

表5　车辆动力响应最大值Table 5　Maximum dynamic response of vehicle

对图9和图10进行比较分析，可以看到跨中竖向位移和塔顶纵向位移相互关联，如最大值均出现在大约3 s处，在大约9 s时出现反方向最大值，这是由于塔顶通过斜拉索与主梁连接，因此位移出现了相关性，这一相关性符合独塔斜拉桥的力学特点，亦说明有限元计算模型建立的准确性。

3.3　列车动力响应

表5给出了CRH2列车在80~160 km/h行车速度下单线过桥时的车辆响应最大值，表中的脱轨系数为剔除轮轨瞬间脱离数据点后的数值，轮重减载率未考虑动态减载的情况。

由表5可见，动车和拖车的脱轨系数整体上随着行车速度的提高而增大，轮重减载率随着行车速度的提高而增大的趋势不明显。横向力及横竖向加速度数值总体均随着行车速度的提高而增大。脱轨系数最大值为0.22，远小于0.8的限值，轮重减载率最大值为0.42，离0.6的限值也相距较远，故可见在CRH2列车各种行车条件下，列车行车安全性均满足要求，列车的车体横、竖向振动加速度均满足限值要求，列车乘坐舒适性均达到“良好”及以上标准。

4　结论

1) CRH2列车通过桥梁时，桥梁的最大横、竖向位移及振动加速度均较小，表明该桥的横、竖向刚度均较大，采用槽形主梁的非对称式斜拉桥具有良好的动力特性。

2) 车辆的振动响应大致上随行车速度的增快而增大，在文中计算条件下，列车的动力响应均在安全限值以内，列车在桥上的行车安全性能很好地满足要求；列车的车体竖、横向加速度满足限值要求，列车乘坐舒适性良好。采用槽形主梁的非对称式斜拉桥具有良好的列车走行性。

参考文献：

[1] 关淑萍, 李江林. 独塔单索面预应力混凝土斜拉桥静载试验[J]. 桥梁建设, 2012(2): 53−58.GUAN Shuping, LI Jianglin. Static load testing Of a PC cable-stayed bridge with a single pylon and single cable plane[J]. Bridge Construction, 2012(2): 53−58.

[2] 徐略勤, 李建中. 曲线梁独塔斜拉桥的抗震分析模型探讨[J]. 结构工程师, 2011, 27(1): 98−104.XU Lueqin, LI Jiangzhong. Discussion on finite element models for seismic analysis of a curved cable-stayed bridge with single pylon[J]. Structural Engineers, 2011,27(1): 98−104.

[3] 王伟, 韦正华, 袁万城. 独塔双索面斜拉桥抗震性能研究[J]. 中外公路, 2013(2): 163−166.WANG Wei, WEI Zhenghua, YUAN Wancheng. A single pylon and double cable plane cable-stayed bridge seismic performance research[J]. Journal of China & Foreign Highway, 2013(2): 163−166.

[4] 黄侨, 陈卓异, 荣学亮, 等. 波形钢腹板预弯槽形梁的应力分析与试验研究[J]. 桥梁建设, 2013(5): 42−48.HUANG Qiao, CHEN Zhuoyi, RONG Xueliang, et al.Stress analysis and experimental study of preflex trough girder with corrugated steel webs[J]. Bridge Construction.2013(5): 42−48.

[5] 韩江龙, 吴定俊, 李奇. 板厚和加肋对槽型梁结构噪声的影响[J]. 振动工程学报, 2012(5): 589−594.HAN Jianglong, WU Dingjun, LI Qi. Influence of deck thickness and stiffeners on structure-borne noise of the trough beams[J]. Journal of Vibration Engineering,2012(5): 589−594.

[6] 黄侨, 陈卓异, 杨明. 槽型梁桥力学性能的研究现状与展望[J]. 中外公路, 2013, 33(6): 131−136.HUANG Qiao, CHEN Zhuoyi, YANG Ming. Present situation and prospect of research on mechanical properties of channel girder bridge[J]. Journal of China &Foreign Highway, 2013, 33(6): 131−136.

[7] 田杨, 邓运清, 黄胜前. 双线铁路曲线简支槽形梁的空间分析[J]. 铁道工程学报, 2012(7): 24−28.TIAN Yang, DENG Yunqing, HUANG Shengqian. The spatial analysis of curved simple trough girder with two-lane railway[J]. Journal of Railway Engineering Society, 2012, 7(7): 24−28.

[8] 吴亮秦, 吴定俊, 李奇. 城市轨道交通薄壁槽形梁车桥动力特性试验研究[J]. 中国铁道科学, 2011, 32(4):31−37.WU Liangqin, WU Dingjun, LI Qi. Experimental study on vehicle-bridge dynamic characteristics of thin-walled trough girder bridge for urban rail transit[J]. China Railway Science. 2011, 32(4): 31−37.

[9] 戴公连, 粟淼, 闫斌, 等. 槽形梁斜拉桥塔梁固结区受力分析及构造细节[J]. 桥梁建设, 2013(4): 61−67.DAI Gonglian, SU Miao, YAN Bin, et al. Mechanical analysis and structural details of pylon and girder rigid fixity zone of a channel girder cable-stayed bridge[J].Bridge Construction, 2013(4): 61−67.

[10] 朱志辉, 王小飞, 吕连兵, 等. 卸索期间列车—斜拉桥耦合动力响应分析[J]. 中国铁道科学, 2015, 36(5):19−27.ZHU Zhihui, WANG Xiaofei, LÜ Lianbing, et al.Coupling dynamic response of train and cable-stayed bridge during cable removal[J]. China Railway Science,2015, 36(5): 19−27.

[11] 陈淮, 祁冰, 杜晓伟. 大跨双槽渡槽横向地震响应分析[J]. 地震工程与工程振动, 2004, 24(5): 118−122.CHEN Huai, QI Bing, DU Xiaowei. Lateral seismic response analysis of large-scale double cell aqueduct[J].Earthquake Engineering and Engineering Vibration. 2004,24(5): 118−122.

[12] 徐建国, 陈淮, 王博, 等. 大型渡槽结构考虑流固耦合的动力建模研究[J]. 南京理工大学学报(自然科学版),2005, 29(6): 639−644.XU Jianguo, CHEN Huai, WANG Bo, et al. Dynamic modeling study of aqueduct structure with fluid-structure coupling[J]. Journal of Nanjing University of Science and Technology, 2005, 29(6): 639−644.

[13] 曾庆元. 弹性系统动力学总势能不变值原理[J]. 华中理工大学学报, 2000, 28(1): 1−3.ZENG Qingyuan. The principle of total potential energy with stationary value in elastic system dynamics[J].Journal of Huazhong University of Science and Technology, 2000, 28(1):1−3.

[14] 曾庆元, 向俊, 娄平. 车桥及车轨时变系统横向振动计算中的根本问题与列车脱轨能量随机分析理论[J]. 中国铁道科学, 2002, 23(1): 3−12.ZENG Qingyuan, XIANG Jun, LOU Ping. Fundamental problems in calculation of transverse vibration of train-bridge and train-track time-varying system and theory of energy random analysis for training derailment[J]. China Railway Science. 2002, 23(1): 3−12.

[15] 苗永抗, 郭向荣. 辅助墩对混合梁斜拉桥列车走行性影响研究[J]. 铁道科学与工程学报, 2016, 13(5): 876−881.MIAO Yongkang, GUO Xiangrong. Analysis of the influence of auxiliary piers to the coupled vibration of vehicle and long span cable-stayed bridge with hybrid girder[J]. Journal of Railway Science and Engineering.2016, 13(5): 876−881.

[16] 朱志辉, 龚威, 王力东, 等. 列车−轨道−桥梁耦合系统动力方程求解方法对计算精度和效率的影响[J]. 中国铁道科学, 2016, 37(5): 17−26.ZHU Zhihui, GONG Wei, WANG Lidong, et al.Influence of solution method for dynamics equation of train-track-bridge coupled system on calculation precision and efficiency[J]. China Railway Science, 2016,37(5): 17−26.

[17] 朱志辉, 王力东, 杨乐, 等. 轨道不平顺短波分量对列车−简支梁桥耦合振动的影响[J]. 中国铁道科学, 2016,43(1): 53−60.ZHU Zhihui, WANG Lidong, YANG Le, et al. Effect of short-wavelength components in rail irregularity on the coupled dynamic responses of train and simple-supported bridge[J]. Journal of Hunan University, 2016, 43(1):53−60.