“羊吃草的面积”教学实录

2018-04-03张齐华

小学教学(数学版) 2018年10期

◇张齐华

一、引入

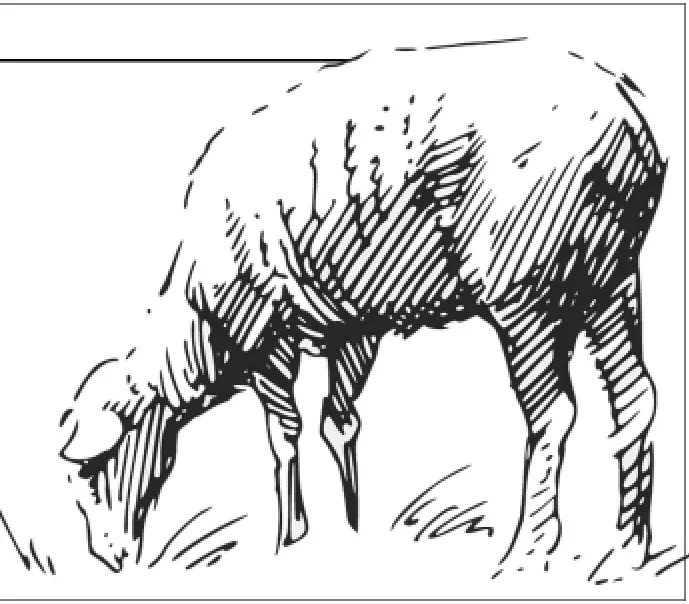
师：今天这节课，我们一起来研究和“羊吃草”有关的问题。瞧，这是一个封闭的正方形羊圈，羊圈外面全部是草地（如图1）。假设草地上有一根绳子，绳子一端系在固定的桩子上，另一端系着一只羊。要想知道这只羊最多能吃多大面积的草，你有什么好办法？有没有什么问题？

图1

学生思考片刻后，组内交流，随后全班学生交流。

生：我觉得这个问题不确定，你得看这根桩子到底在哪里。如果这根桩子在草地中间，那么，羊吃草的面积就是一个圆形，圆的面积取决于绳子的长度。

生：我也觉得不能确定。除了看桩子在哪里，还得看绳子有多长。假定桩子在这里（手指屏幕比画），如果绳子比较短，那么最后的面积就是以绳子为半径的圆的面积。但是，如果绳子比较长，超过了桩子到羊圈的距离，那么，我们求出圆的面积后，还得减去羊圈挡住的那部分面积。因为，羊圈里面是没有草的。再说，这是一个封闭的羊圈，羊也进不去。

生：我觉得，桩子的位置也很重要。刚才两位同学提到的桩子都在草地中间。如果桩子就在羊圈边上，比如在羊圈一边的中点上，那么，羊吃到的草的面积，就不是一个完整的圆，而是一个半圆了。

生：我觉得不一定是半圆，有可能要比半圆大。具体取决于绳子的长度：如果绳子的长度小于或等于羊圈的边长的一半，那么就是一个半圆。如果绳子的长度大于羊圈的边长的一半，那么就不是一个半圆了，比较复杂。

生：如果桩子放在羊圈的一个顶点上，情况又不一样了。而且，也和绳子的长度有关。如果绳子短一点，问题还比较简单。如果绳子比较长，那么，问题就会变得复杂起来。

师：张老师很奇怪。其实，在前面的练习课上，我们遇到过羊吃草问题的，好像就是一个圆的面积。为什么今天的羊吃草，听起来却要复杂很多？

生：那是因为多了一个羊圈。

生：是羊圈让问题变得复杂了很多。

生：不光是羊圈，还和桩子的位置、绳子的长度有关。

师：看来，一个看起来简单的数学问题，一旦增加一些要素，有时哪怕只增加一个要素，问题就会变得复杂起来。这就是数学的神奇之处！

二、探究

今天这节课，我们就来讨论其中的一种情况——桩子在羊圈的顶点上。（在正方形羊圈的右下角顶点处标出桩子的位置）现在，要想解决羊能吃多大面积的草，你还需要了解哪些信息？

生：我需要了解绳子的长度。

生：我需要了解羊圈的边长。

师：已知羊圈的边长是4米。这儿有2根不同的绳子，长度分别是3米和6米。如果不考虑拴绳用去的长度，也不考虑羊自身的大小。你能大胆想象一下，绳长3米时，羊吃到的草，可能是个什么形状吗？如果绳长6米呢？

学生独立思考、大胆想象，并结合作业纸上的示意图，比画并描述羊可能吃草的区域。随后，全班交流。（略）

师：看来，当绳长3米时，大家的观点比较一致。当绳长6米时，还有些争议。接下来，就让我们带着问题和思考，亲自动手来研究研究，看看究竟哪一种方案才是正确的。研究过程中，如果遇到困难，建议大家在示意图上画一画，把自己的想象落到纸上。也可以借助老师给大家提供的羊圈模型和绳子，亲自动手转一转、比画比画。或许，动手的过程，会给你们带来新的启示。

学生组内交流，或借助模型动手操作以明确思路，或画示意图帮助理解，最终列式计算解决问题。随后全班分享。

师：绳长3米时，羊最多能吃多少面积的草？谁愿意分享你们的思路？

生：我们小组经过研究发现，绳长3米时，这只羊能够吃草的面积，应该是一个圆的（如图2）。因为我们已经知道，当没有羊圈阻挡时，羊吃草的区域应该是一个半径为3米的圆。但现在，因为桩子在羊圈的顶点上，羊不可能吃到整个圆，只能是这一部分，而这部分正好是圆的。所以，最终羊吃到的草的面积应该是半径为3米的圆面积的，π×3×3×=π(平方米)。

图2

师：谁还有补充？

师：有没有哪个小组，遇到过困难的？

生：我们一开始只知道比一个整圆要小，但到底小多少不太清楚。但后来我们画了一幅图，思路就清楚了，应该是整个圆的。

师：看来，画图的确可以帮助我们理解问题，找到解决问题的思路。绳长3米时，看来大家没有什么困难。那么，绳长6米时，羊最多又能吃多少面积的草呢？

生：我们发现，当绳长6米时，画出来的圆已经把整个羊圈都盖住了（如图3）。所以，羊最多能够吃草的面积，相当于用这个圆的面积，减去羊圈的面积。π×6×6-4×4=36π-16（平方米）。

图3

师：对于他们的想法，谁有质疑或补充？

生：我觉得这种方法不对。因为有羊圈挡着，所以，羊不可能走成一个整圆的，比如这里（指正方形左上角），羊就到不了。所以，我们觉得，羊最终能够吃草的面积，也是一个圆的，只不过圆的半径不是3米，而是6米（如图4）。计算的方法和原来的差不多，π×6×6×=27π(平方米)。

图4

生：我也觉得第一种方法不对，但第二位同学的方法也有问题。我们小组经过研究，发现羊能够吃草的最大面积，应该是这样的（如图5）。这里也是一个圆的，半径是6米。由于绳子长度已经超过4米，所以拐个弯以后，这里还有两个圆，合在一起相当于一个半圆。加起来，总面积应该是(平方米)。

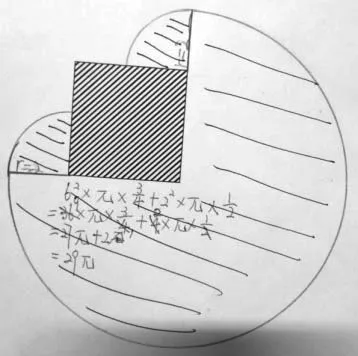
图5

师：出现了三种不同的答案，听起来各有各的道理。究竟哪一种才是正确的？你能给出更有说服力的解释吗？小组里交流交流。（小组交流略）

师：请交流你们现在的想法。

生：我们觉得第三种思路是正确的。大家可以看我演示一下（如图6）。为了吃到更多的草，羊一定会把绳子绷得直直的。那么，从这儿到那儿，画出来的就是一个圆的。但是，到了这儿以后，由于绳子被羊圈挡住了，所以，这个圆画不下去了，只能用剩下的2米继续往下画，从这儿到那儿，还能画一个小圆的。当然，在另一端，情况也是一样的。所以，最后羊能够吃草的面积，应该是一个大圆的，加上两个小圆的。

图6

师：听完他的介绍后，你现在更认同哪一种方法？

生：第三种方法。

师：奇怪，一开始不少同学选择了方法一和方法二，为什么现在大家都选择方法三了？

生：因为我觉得第三种方法最有道理。原来我们没有考虑到羊圈的阻挡，还以为仍然可以画一个整圆。

生：我们原来没有考虑到绳子还可以继续往下转。

生：我觉得，是因为这位同学在黑板上给我们动手演示了一遍。他一演示，我就发现原来的思路错了，他的思路才是对的。

师：面对一个复杂的数学问题，借助头脑展开空间想象固然好。但有时候动手画一画，必要的时候再亲自用学具演一演，可以帮助我们更好地找到解决问题的思路。这一点，希望对大家能有一些启发！

三、拓展

师：不过，一个真正优秀的问题解决者，不能只满足于解决老师给我们提供的问题。我们还得进一步作深入的思考。比如，就这个问题而言，大家有没有想过，同样是正方形羊圈，同样用一根绳子拴在羊圈的顶点上，为什么两道题的解题思路看起来很不一样？

生：我觉得是因为绳子的长短不一样。

师：仅仅是因为绳子的长短不一样吗？或者说，改变绳子的长短，一定会带来解决问题思路的变化吗？这样，自己换一换绳子的长度，看看你有什么新发现！

学生先独立思考，改变数据并尝试计算。随后小组交流，分享自己的发现。最后全班交流。

生：我们发现，改变绳子的长度，并不一定会影响最后的计算方法。比如，如果这根绳子长2米或1米，羊吃草的面积虽然会变化，但计算方法不变，还是计算圆面积的，因为最后的思路还是一样的。

生：我发现，绳子长4米时，计算的方法也是一样的，也是一个圆的。

生：我觉得，绳子的长度在1～4米时，计算的方法都一样，哪怕绳子的长度是一个小数，结果都是一个圆的。

生：我想补充，我觉得不只是1～4米，应该是0～4米。当绳子长0～4米时，最后都是一个圆的。

生：我觉得，当绳子的长度超过4米时，答案就应该是一个圆的，加上2个圆的了。

生：我反对！因为，当绳子的长度超过8米时，绳子又拐过了第二个弯，答案又不一样了。

生：我觉得，当绳子的长度是0～4米时，最后的答案就是一个圆的。当绳子的长度是4～8米时，当然不包括4米，这时的答案就是一个大圆的和2个小圆的。而当绳子的长度是8～12米时，当然不包括8米，这时的答案应该是一个大圆的，加上两个小圆的，然后再加上两个更小圆的。

师：听起来，这有点复杂了。这样，我们继续往下讨论，你能试着画一画示意图，或借助学具演示一下，然后给我们分享一下你的思路吗？

生：可以！

该学生画图研究，课堂讨论继续。

师：回顾刚才的过程，有没有发现，在羊吃草这个问题上，随着绳子长度的变化，好像存在着一个变与不变的问题。谁发现了？

生：我发现，当绳子的长度超过羊圈的边长时，解题的思路就开始发生变化。而当绳子的长度超过羊圈边长的两倍时，解题的思路又开始发生变化。

生：我发现，这里的4米和8米就像一个分水岭。没有到达“分水岭”之前，解题的方法都是一样的。一旦过了“分水岭”，方法就发生变化了。

师：多么形象的比方！解决问题的过程中，有时的确会存在“分水岭”。关键是，我们要准确地找到“分水岭”在哪里，然后弄明白“分水岭”前后的区别，以便于我们准确找到最适合的解决问题的方法。刚才这位同学经过尝试，已经找到了自己的解决问题的方法，让我们听听他是怎么解决这一问题的。

生：我发现，当绳子的长度超过8米后，绳子的确会第二次拐弯（如图7）。我举了个例子，比如绳子的长度是8.5米。这时候，我发现，羊吃草的面积，除了一个大圆的，两个小圆的，还有两个更小的圆。只不过，最后的答案不是用这三部分加起来，因为这里有些部分已经重叠在一起了。所以，最后的面积要比一个大圆的和两个小圆的的面积总和小一些，因为我们要把重叠的部分减掉。但到底减去多少，我觉得非常复杂，没法计算了。