ON THE UNIQUENESS OF ELLIPSOID SOLUTIONS TO THE Lp-MINKOWSKI PROBLEM

LI Si-yuan

(School of Mathematics and Applied Statistics,Faculty of Engineering and Information Sciences,University of Wollongong,Wollongong NSW 2522,Australia)

1　Introduction

The Minkowski problem was popular for more than one hundred years.It had a significant impact on 20th century mathematics.Lp-Minkowski problem introduced by Lutwak[1]was intensively studied in recent decades.There existed many good references on the Lp-Minkowski problem[1–24].However,very little is known on the uniqueness of the Lp-Minkowski problem for p＜1,even in R3.

In this paper,we discuss the uniqueness of Lp-Minkowski problem for all p∈R in general dimensions under the assumption that the solutions are ellipsoids centered at the origin,which needs to study the following Monge-Amp`ere equation

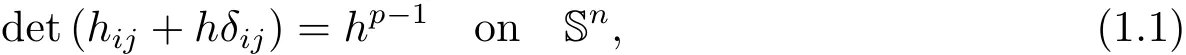
where h is the support function(see Definition 2.1)of convex bodies,hijare the second-order covariant derivations of h with respect to any orthonormal frame{e1,e2,···,en}on the unit sphere Sn,δijis the Kronecker delta and p∈ R.Similarly,we obtain the uniqueness for the Christoffel-Minkowski problem of Lp-sum under the same assumption,which needs to study a k-Hessian equation as follows

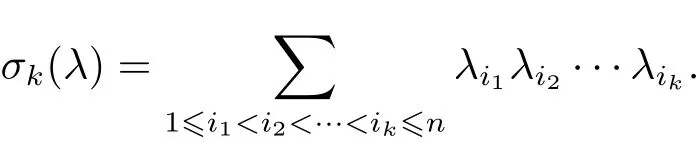
The definition can be extended to a symmetric matrix W ∈ Rn×nby σk(W)= σk(λ(W)),where λ(W)is the eigenvalue vector of W.

(1.1)comes from the geometry of convex bodies.A compact convex subset of Euclidean space Rn+1with a nonempty interior is a convex body.Minkowski developed a few basic concepts on convex bodies:support function,Minkowski sum and mixed volumes(see,e.g.[9,25]).

The classical Minkowski problem asks the existence of a convex body whose surface area measure is prescribed.It was studied by[26–34](or see[9]for history)and many others.The uniqueness of solutions to the classical Minkowski problem was solved by the Brunn-Minkowski inequality(Gardner gave some equivalent inequalities in[35]):let Q1,Q2⊂Rn+1be two convex bodies and 0＜λ＜1,then

where Vol(·)denotes the volume of a convex body and ‘+’denotes the Minkowski sum(see Definition 2.2).The equality in(1.3)holds if and only if Q1and Q2are translates.

Firey[36]extended the Minkowski sum to the general cases for p≥1,which is called Lp-sum(see Definition 2.3).Later,in[1],Lutwak generalized the classical surface area measure(see Definition 2.5)to the Lpsurface area measure(see Definition 2.6)for p≥1 and studied the generalised Minkowski problem,which was called Lp-Minkowski problem thereafter.Given a finite Borel measure m on Sn,the Lp-Minkowski problem concerns whether there exists a unique convex body Q⊂Rn+1such that m is the Lpsurface area measure of Q.Let µ denote the surface area measure of Q,then the Lp-Minkowski problem is equivalent to solving the equation

where h denotes the support function of Q.Obviously,the classical Minkowski problem is a special case of Lp-Minkowski problem for p=1.In the smooth category,(1.4)is equivalent to considering the following Monge-Amp`ere equation

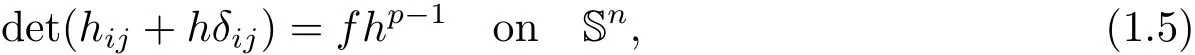
where f is a positive continuous function on Sn.

Lutwak[1]proved the existence of solutions to(1.4)when p＞1,except for p=n+1,under an evenness assumption.Then in[2],Lutwak and Oliker obtained a C∞solution to the even Lp-Minkowski problem for p＞1.Lutwak,Yang and Zhang[6]obtained the existence of solutions to discrete and non-discrete Lp-Minkowski problems with a normalized volume for all p＞1,still under the evenness assumption.Without the evenness assumption,Chou and Wang[8]solved(1.5)for general measures for p＞1.In addition,Hug,Lutwak,Yang and Zhang[7]obtained a different proof of the existence of solutions to the Lp-Minkowski problem for p＞n+1 and to the discrete measure for p＞1.A C2,αsolution to(1.5)for p≥n+1 was given by Chou and Wang[8]and Guan and Lin[14]independently.When 1＜p＜n+1,the solution convex body may have the origin on the boundary(see,e.g.[8,7]),thus it is not necessary to discuss the C2,αregularity.However,for the discrete case,Hug,Lutwak,Yang and Zhang[7]obtained that the solution polytope always has the origin in its interior for p＞1 with p/=n+1.

The cases p＜ 1 are difficult to settle.Chou and Wang[8]got the weak solution to(1.5)when −n−1 ＜ p ＜ n+1.Also,some special cases were studied.In[10],Böröczky,Lutwak,Yang and Zhang gave the existence of solutions to the even L0-Minkowski problem.Zhu[11]studied the discrete L0-Minkowski problem without the evenness assumption.In R2,Stancu[4]studied the discrete L0-Minkowski problem.And in R3,Firey[37]built a mathematical model to describe the ultimate shape of worn stones.This is a parabolic problem related to the L0-Minkowski problem when f is a constant.Chou and Wang studied the critical case p=−n−1 in[8].In[38],Lu and Wang established the existence of rotationally symmetric solutions of(1.5)for p=−n−1(see[39,22]).When p=−n−1 and f≡1,all solutions to(1.5)are ellipsoids centered at the origin,see[40–42].

The uniqueness of Lp-Minkowski problem for p＞1 and p/=n+1(the uniqueness upto a dilation when p=n+1)was solved by the Brunn-Minkowski-Firey inequality[1]:let Q1,Q2⊂Rn+1are two convex bodies that contain the origin in their interiors,p＞1 and 0＜λ＜1,then

where ‘+p’is the Lp-sum and ‘◦’is the Firey multiplication.The equality in(1.6)holds if and only if Q1=Q2.However,the uniqueness for p ＜ 1 is difficult and still open because the Brunn-Minkowski inequality for p＜1 is still open.In[12],Jian,Lu and Wang obtained that for any−n−1＜p＜0,there exists a positive function f∈C∞(Sn)to guarantee that(1.5)has two different solutions,which means that we need more conditions to consider the uniqueness.The uniqueness results of polygonal L0-Minkowski problem in R2were given by Stancu in[5].And in R3,Huang,Liu and Xu[13]obtained the uniqueness of Lp-Minkowski problem for−1≤p＜1 when f≡1 for the C4smooth convex bodies.Chen and Zhou obtained the generalised dual Minkowski inequalities in[43].

Christoffel-Minkowski problem arises in the study of surface area functions and it asks the existence of a convex body Q whose k-th elementary symmetric function of all principal radii of the boundary is prescribed[9].It needs to solve a k-Hessian equation

where σkis the k-th elementary symmetric function defined in the beginning.When k=n,(1.7)is the classical Minkowski problem.A necessary condition for(1.7)to have a solution[33]is

Guan and Ma[46]gave a sufficient condition for the existence of a unique convex solution to(1.7),and Guan,Ma and Zhou[3]proved(1.8)is sufficient for(1.7)to have an admissible solution.The convex solution and admissible solution are defined in Definition 2.7.

Similarly,we can consider the Lpanalog of Christoffel-Minkowski problem,which we call the Christoffel-Minkowski problem of Lp-sum,or equivalently

When p=1,(1.9)is reduced to(1.7),and when k=n,(1.9)is reduced to(1.5).When p≥k+1 and 1≤k＜n,under the condition that the function 0＜f∈Cm(Sn)(m≥2)satisfiesonSn,Hu,Ma and Shen[45]obtained the Christoffel-Minkowski problem of Lp-sum has a unique convex body that has the origin in its interior with a Cm+1,α(0＜α＜1)boundary(the uniqueness upto a dilation when p=k+1).The uniqueness of(1.9)for 1＜p＜k+1 can be obtained via the Alexandrov-Fenchel inequality[44].However,the uniqueness of(1.9)for p＜1 is still open.

In this paper,we consider the uniqueness of Lp-Minkowski problem and Christoffel-Minkowski problem of Lp-sum for p＜1 when the solutions to(1.1)and(1.2)are ellipsoids centered at the origin.

Our main result is

Theorem 1.1If the solution to(1.1)is an ellipsoid centered at the origin,then the uniqueness holds for any p∈ R{−n−1}(the uniqueness holds upto a dilation when p=n+1).And when p= −n−1,the solutions to(1.1)are all ellipsoids centered at the origin with a volume ωn+1,where ωn+1is the volume of the unit ball in Rn+1.

Theorem 1.2If the solution to(1.2)is an ellipsoid centered at the origin,then the uniqueness holds for any p∈R(the uniqueness holds upto a dilation when p=k+1).

The organization of this paper is as follows:after the preliminary Section 2,we discuss the ellipsoid solutions of Lp-Minkowski problem(Theorem 1.1)in Section 3.Then in Section 4,we prove Theorem 1.2.

2　Preliminary

Associated with a convex body is its support function.

Definition 2.1Let Q⊂Rn+1be a convex body and M be its boundary.The support function of Q(or M)is defined by

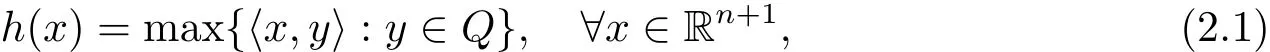
where〈·,·〉denotes the inner product in Rn+1.

If M is smooth and strictly convex,then it can be represented by its inverse Gauss map ν:Sn→M.Then the support function of M can be represented by

and be positively homogeneous degree 1 after being extended to Rn+1by h(x)=|x|h(x/|x|)for all x∈Rn+1.

Clearly,the support function of a convex body is convex and positively homogeneous degree 1,thus it is determined by its value on Sncompletely.Conversely,any continuous function h on Sn,which can be convex after being extended to be positively homogeneous degree 1 on Rn+1,can determine a convex body by

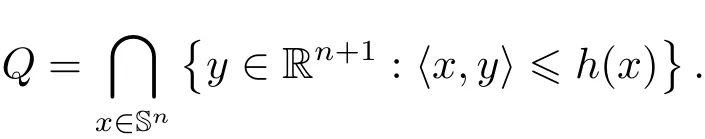
Definition 2.2Given two convex bodies Q1,Q2∈K with respective support function h1and h2,and λ,µ ≥ 0(λ2+µ2＞ 0),the Minkowski sum λQ1+ µQ2∈ K is defined by the convex body whose support function is λh1+ µh2,which means

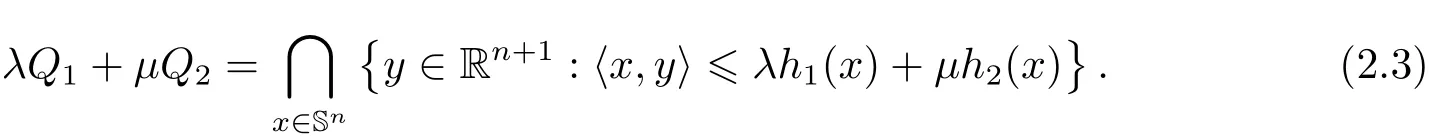
Let K0collect convex bodies in K that contain the origin in their interiors.In 1962,Firey[36]generalized the concept of Minkowski sum from p=1 to Lp-sum for p≥1 as follows.

Definition 2.3For p≥1,given two convex bodies Q1,Q2∈K0with respective support function h1and h2,and λ,µ ≥ 0(λ2+ µ2＞ 0),the Lp-sum λ◦Q1+pµ ◦Q2∈ K0is the convex body with support functionwhich means

where ‘+p’means the Lpsummation and ‘◦’means Firey multiplication.

It is clear that λ◦Q= λ1pQ.And if p=1,they are equal.

Furthermore,we consider the set of positive support functions in S,denoted by S0,i.e.,S0=S∩{h＞0}.Then we can further extend the Lp-sum(2.4)to any p∈R.For 0＜λ＜1 and a,b＞0,define

Mp(a,b,λ)is increasing with respect to p,namely,if−∞≤ p＜q≤∞,then

where Mp(a,b,λ)=Mq(a,b,λ)if and only if a=b＞ 0.

Definition 2.4For Q1,Q2∈K0with respective support function h1,h2∈S0,λ∈(0,1)and p∈R,the generalised Lp-sum is

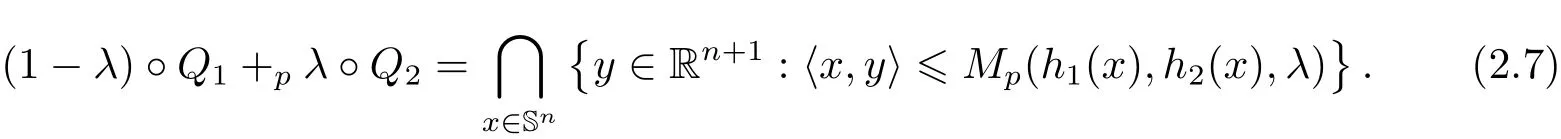
It is obvious that when p≥1,the convex body defined by(2.7)is the Lp-sum(2.4).

Definition 2.5Suppose Q ∈ K,the surface area measure S(Q,·)of Q is a Borel measure defined on Sn,such that

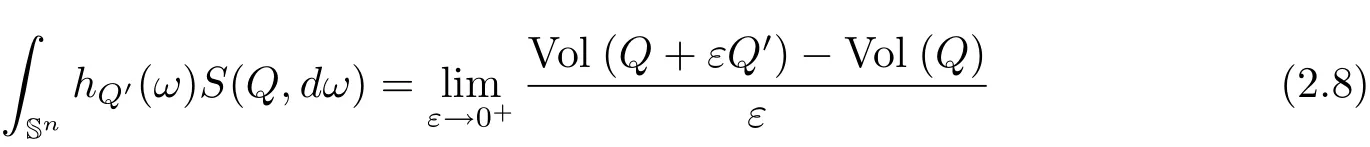
for any convex body Q′∈ K,where hQ′is the support function of Q′and Q+ εQ′is the Minkowski sum defined in Definition 2.2.

Definition 2.6For p ≥ 1 and Q ∈ K0,the Lpsurface area measure Sp(Q,·)of Q is a Borel measure defined on Snsatisfying

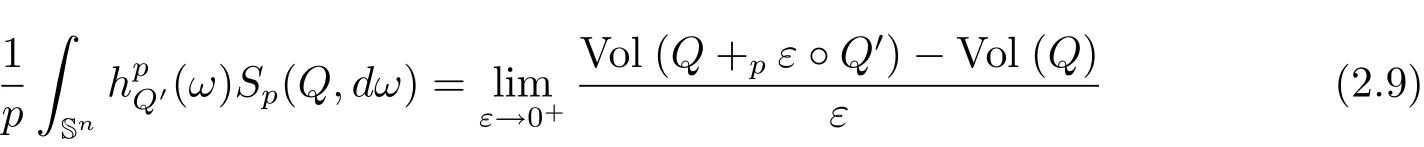
for any convex body Q′∈ K0,where Q+pε◦Q′is the Lp-sum defined in Definition 2.3.

The relationship between the classical and Lpsurface area measure is

Definition 2.7A function u ∈ C2(Sn)is called convex if(uij+uδij)＞ 0 on Sn.For 1≤ k ≤ n,let Γkbe the convex cone in Rndetermined as

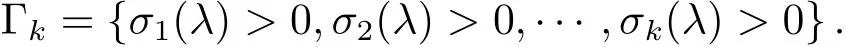
Suppose u∈ C2(Sn),we say u is k-convex if for any x∈ Sn,W(x)={uij(x)+u(x)δij}∈ Γk.Furthermore,u is called an admissible solution to(1.7)if u is k-convex and satisfies(1.7).

Now we represent the Gauss curvature of a convex body by its support function.

Assume that M⊂Rn+1is a smooth,closed and uniformly strictly convex hypersurface enclosing the origin and parameterised by its inverse Gauss map ν :Sn→ M.Let h be the support function of M,{e1,e2,···,en}be the local orthonormal frame on Snand ▽ibe the covariant differentiation on M along the direction ei.Differentiate(2.2)twice along eiand ej,then we have

where Gijis the second fundamental form of M.The details can be found in[47].Let gijbe the metric of M,then according to the relation▽ix=Gikgkm▽mν,we have

thus

Due to the uniformly convexity of M,the Gauss curvature K of M can be represented by its support function as follows

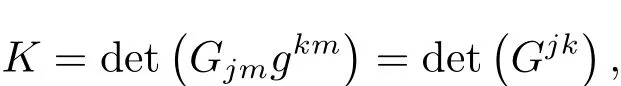
by(2.11),we have

Remark 2.8The principal radii of M are eigenvalues of matrix{hij+hδij}.

3　Proof of Theorem 1.1

We can see that h=1 is a solution to(1.1).Denote M by the boundary of the ellipsoid centered at the origin in Theorem 1.1.To prove the uniqueness of solutions to(1.1),we need to prove that M is a unit sphere when p∈R{−n−1,n+1}.Choose a suitable orthonormal frame on Rn+1such that M is in the following form

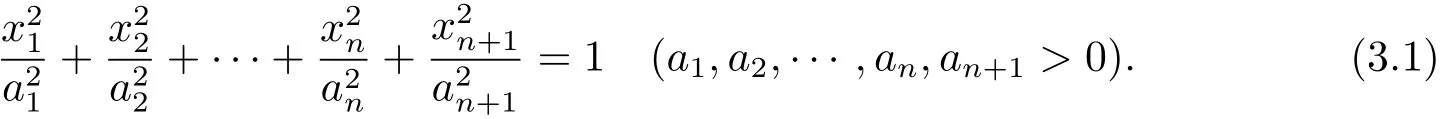
Setting p0=p−1,according to(2.13),(1.1)is equivalent to where K is the Gauss curvature of M and h is the support function of M.

3.1　The Gauss Curvature K of M

The lower semi-surface of M is

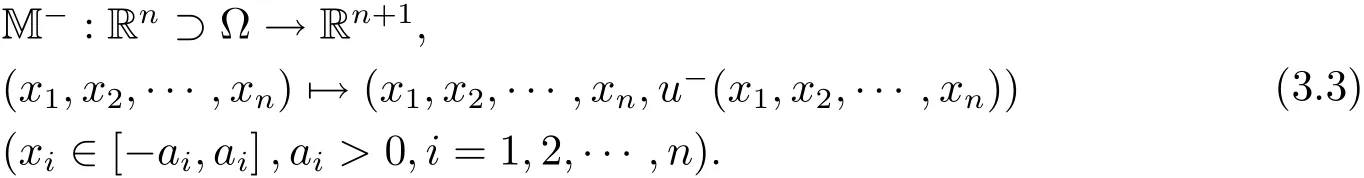
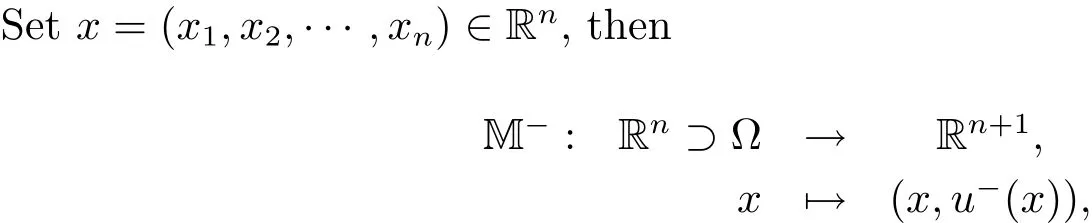
where

then M−is the graph of u−.Set

then u−=−u+.When u+/=0,we have

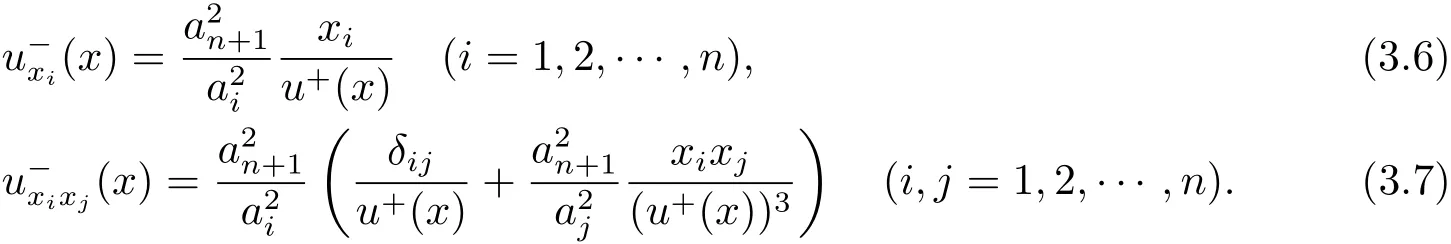
Then

In the third equality above,we have used

where λ∈R is a constant,Amnis a real m×n matrix and Emis a m-order identity matrix.

Also,we have

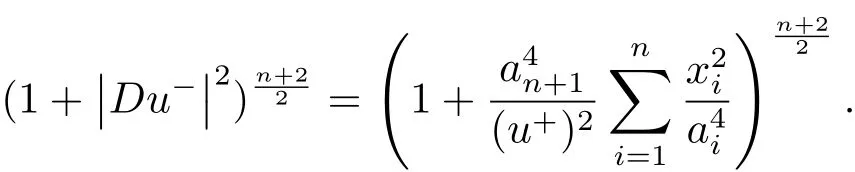
Then the Gauss curvature K−of M−is

By(3.5),we have

According to the symmetry of ellipsoids,the Gauss curvature K of M is

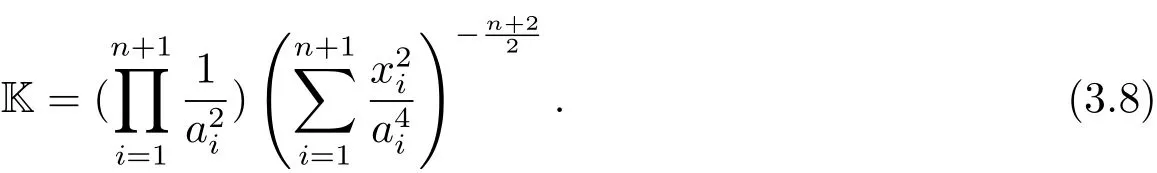
Remark 3.1Although u+is present in the denominator of det(D2u−)and 1+|Du−|2,the quotient K−of them avoids the case.Therefore we can also use(3.8)to obtain the Gauss curvature of M when u+=0 because of the continuity of Gauss curvature of ellipsoids.

3.2　The Support Functionh of M

The unit outer normal at an arbitrary point P=(x1,x2,···,xn,xn+1)on M is

then the support function h at P is

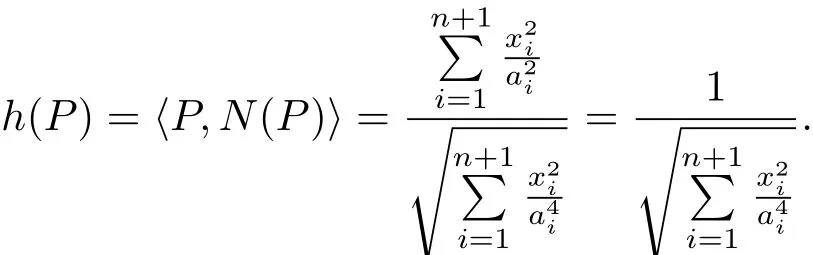
Thus the support function h of M is

3.3　Proof of Theorem 1.1

ProofInserting(3.8)and(3.9)into(3.2),we have

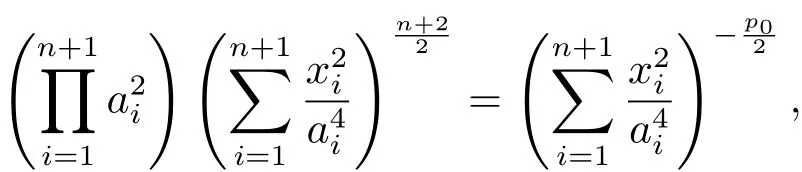
thus In order that(3.10)is true for all P∈ M,for any j ∈ {1,2,···,n+1},pick Pj=(0,···,0,aj,0,···,0)in(3.10),then we have

Then

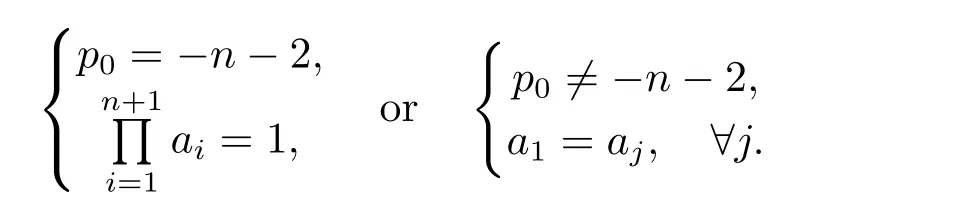
Case 1Whenthe volume of the ellipsoid surrounded by M is a constant ωn+1,where ωn+1is the volume of the(n+1)-dimensional unit ball in Rn+1.

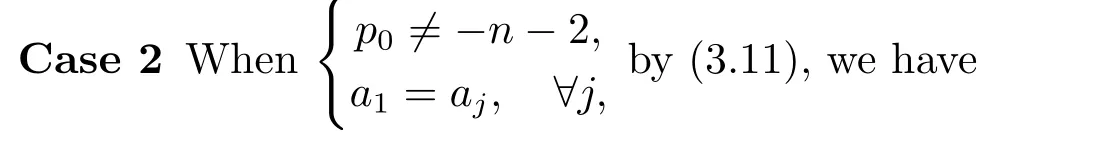
then

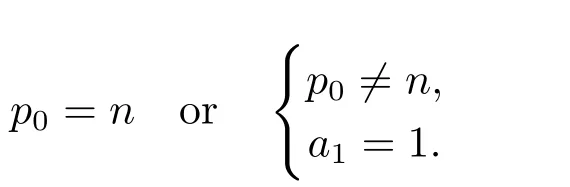
Hence,for all p0∈ R{n,−n−2},M is a unit sphere;when p0=n,M is an arbitrary sphere;when p0=−n−2,the product of all the half-axis of M is 1.

4　Proof of Theorem 1.2

Let M be a uniformly convex hypersurface that can be represented by the graph of a C2function u,then the first and second fundamental form of M are

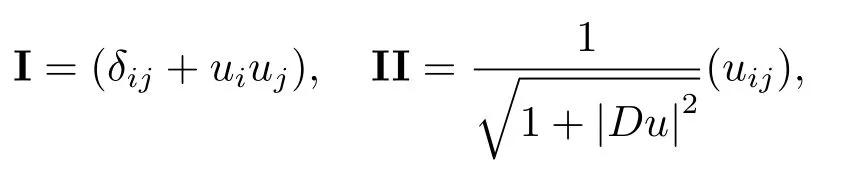
respectively,where Du,(uij)are the gradient and Hessian matrix of u,respectively,and(uij)is invertible because of the uniformly convexity of M.

4.1　Proof of Theorem 1.2 for k=1

When k=1,(1.2)is reduced to

We can see that h=1 is a solution to(1.2).Similarly,let M represented by(3.1)be the boundary of the ellipsoid centered at the origin in Theorem 1.2.To prove the uniqueness of solutions to(1.2),we need to prove that M is a unit sphere when p0∈R{1}.M−is represented by the graph of u−,then denote the inverse matrix of the Hessian matrix of u−by

we have

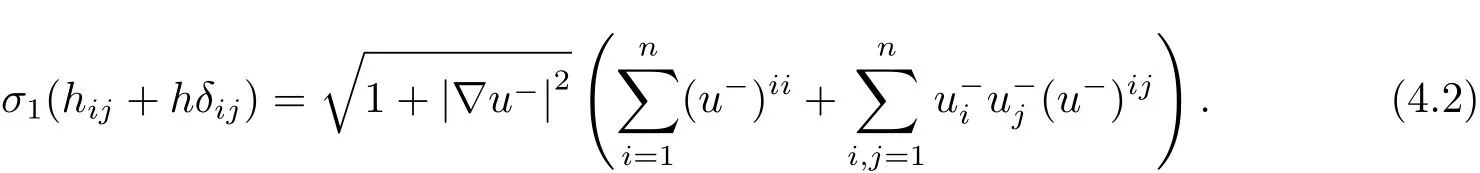
ProofFor the lower semi-surface M−,we have

Inserting(4.3)and(3.9)into(4.1),we have

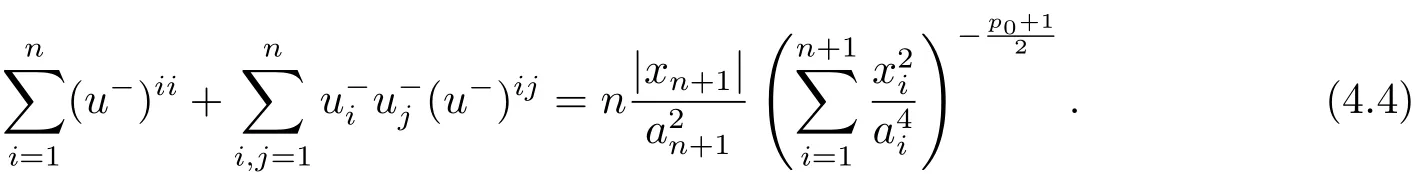
Since

then

and

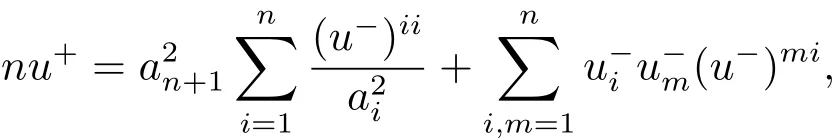
thus(4.4)is equivalent to

In order that(4.5)is true for any P on M−,taking Pn+1=(0,0,···,0,−an+1),we have

For all j ∈ {1,2,···,n}, fixed,at Pj=(0,···,0,aj,0,···,0),we have

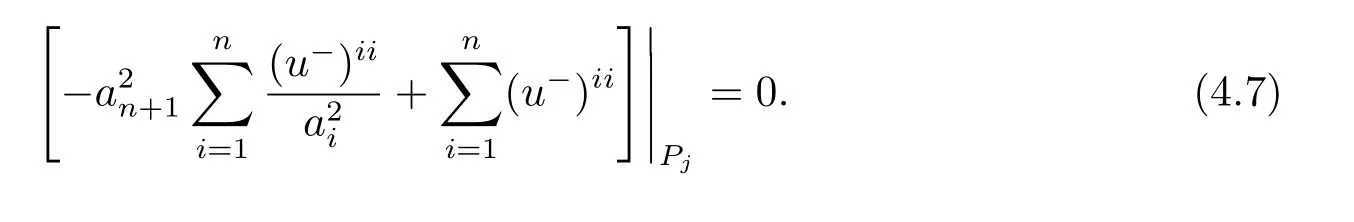
Without loss of generality,assume that

that

then

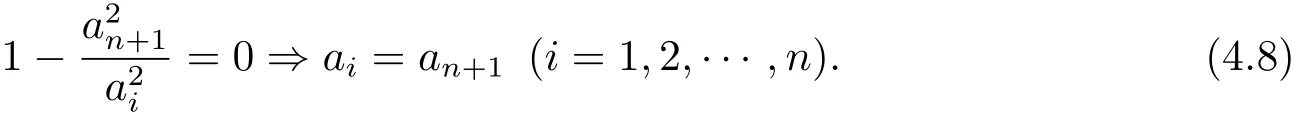
Using(4.8)in(4.6),we obtain

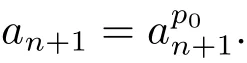
Thus

Hence we obtain the following results:M is a unit sphere for all p0∈R{1},and M is an arbitrary sphere when p0=1.

4.2　Proof of Theorem 1.2 for 1＜k＜n

It is complicated to compute the Hessian matrix((u−)ij)for the intermediate cases

According to the above discussion,we can pick some special points on the boundary first,then calculate the Hessian matrix at these special points,and use equation(4.9)to obtain the conclusion finally.In this part,we need to prove that M is a unit sphere for any p0∈R{k}.

ProofFor the lower semi-surface M−,at point Pn+1=(0,0,···,0,−an+1),according to(3.6),(3.7),we have

then

Thus

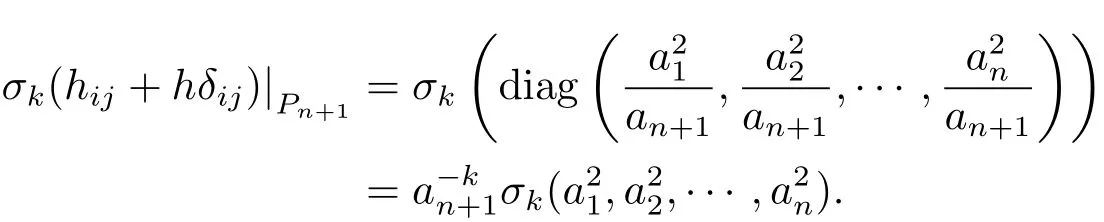
Using(4.9),we have

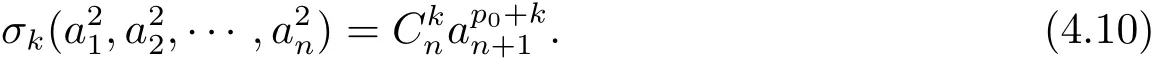
For i=1,2,···,n, fixed,at pointwe have

Then

Hence

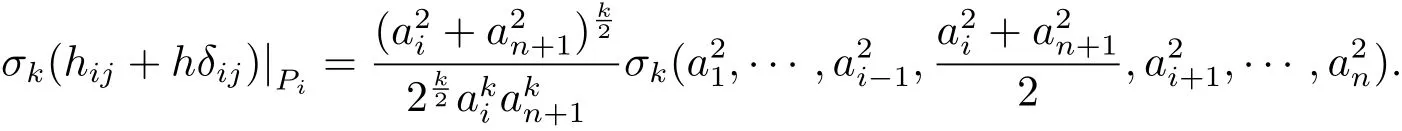
Using(4.9),we have

For k ∈ {2,3,···,n−1},denote

then

Next we prove ai=an+1.

Case 1p0+k≥0.Divided(4.13)by(4.12),we have

If ai≥an+1,then right hand side of(4.14)is

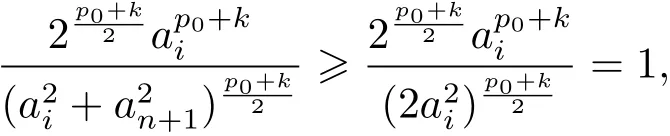
while left hand side of(4.14)is

then

Similarly,if ai≤an+1,we also have ai=an+1.

Case 2p0+k＜0.Subtracting(4.13)from(4.12),we have

Then we prove ai=an+1by contradiction.If ai/=an+1,then Σ1can be represented as

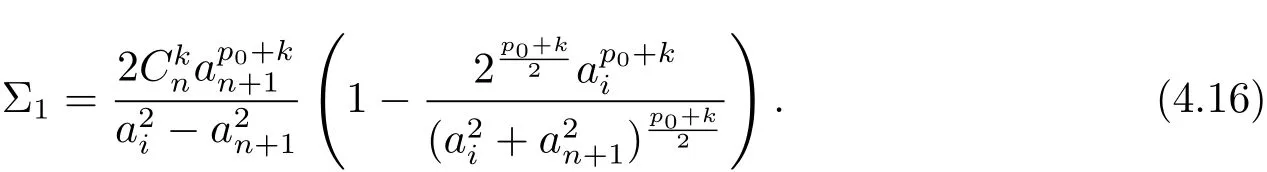
The above equality is equivalent to

The right hand side of(4.17)is positive.If ai＞an+1,then

If ai＜an+1,

then the left hand side of(4.17)is negative.This is a contradiction.

Hence ai=an+1(i=1,2,···,n).

Using(4.10),we have

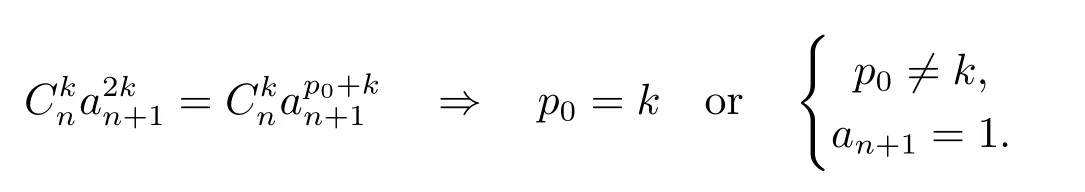
Thus we have

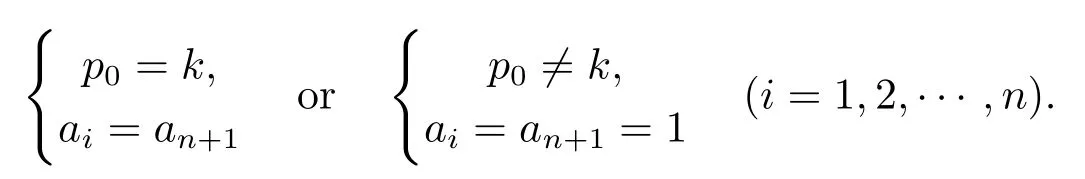
Now we have the following results:for any p0∈R{k},M is a unit sphere,and if p0=k,M is an arbitrary sphere.

Now we complete the proof of Theorem 1.2.

[1]Lutwak E.The Brunn-Minkowski-Firey theory I:mixed volumes and the Minkowski problem[J].J.Diff.Geom.,1993,38(1):131–150.

[2]Lutwak E,Oliker V.On the regularity of solutions to a generalization of the Minkowski problem[J].J.Diff.Geom.,1995,41(1):227–246.

[3]Guan Pengfei,Ma Xinan,Zhou Feng.The Christofel-Minkowski problem III:existence and convexity of admissible solutions[J].Commun.Pure Appl.Math.,2006,59(9):1352–1376.

[4]Stancu A.The discrete planar L0-Minkowski problem[J].Adv.Math.,2002,167(1):160–174.

[5]Stancu A.On the number of solutions to the discrete two-dimensional L0-Minkowski problem[J].Adv.Math.,2003,180(1):290–323.

[6]Lutwak E,Yang D,Zhang Gaoyong.On the Lp-Minkowski problem[J].Trans.Amer.Math.Soc.,2004,356(11):4359–4370.

[7]Hug D,Lutwak E,Yang D,Zhang Gaoyong.On the Lp-Minkowski problem for polytopes[J].Discr.Comput.Geom.,2005,33(4):699–715.

[8]Chou K S,Wang Xujia.The Lp-Minkowski problem and the Minkowski problem in centroaffine geometry[J].Adv.Math.,2006,205(1):33–83.

[9]Schneider R.Convex bodies:the Brunn-Minkowski theory[M].Cambridge:Cambridge University Press,2013.

[10]Böröczky K J,Lutwak E,Yang D,Zhang Gaoyong.The logarithmic Minkowski problem[J].J.Amer.Math.Soc.,2013,26(3):831–852.

[11]Zhu Guangxian.The logarithmic Minkowski problem for polytopes[J].Adv.Math.,2014,262:909–931.

[12]Jian Huaiyu,Lu Jian,Wang Xujia.Nonuniqueness of solutions to the Lp-Minkowski problem[J].Adv.Math.,2015,281:845–856.

[13]Huang Yong,Liu Jiakun,Xu Lu.On the uniqueness of Lp-Minkowski problems:the constant pcurvature case in R3[J].Adv.Math.,2015,281:906–927.

[14]Guan Pengfei,Lin Changshou.On equation det(uij+δiju)=upf on Sn[J].Manuscript,1999.

[15]Andrews B.Gauss curvature flow:the fate of the rolling stones[J].Invent.Math.,1999,138(1):151–161.

[16]Böröczky K J,Heged˝us P,Zhu Guangxian.On the discrete logarithmic Minkowski problem[J].Int.Math.Res.Not.,2016,2016(6):1807–1838.

[17]Böröczky K J,Lutwak E,Yang D,Zhang Gaoyong.The log-Brunn-Minkowski inequality[J].Adv.Math.,2012,231(3):1974–1997.

[18]Chen Wenxiong.LpMinkowski problem with not necessarily positive data[J].Adv.Math.,2006,201(1):77–89.

[19]Haberl C,Lutwak E,Yang D,Zhang Gaoyong.The even Orlicz Minkowski problem[J].Adv.Math.,2010,224(6):2485–2510.

[20]Jian Huaiyu,Lu Jian,Zhu Guangxian.Mirror symmetric solutions to the centro-affine Minkowski problem[J].Calc.Var.Partial Differ.Equ.,2016,55(2):1–22.

[21]Zhu Guangxian.The centro-affine Minkowski problem for polytopes[J].J.Diff.Geom.,2015,101(1):159–174.

[22]Zhu Guangxian.The LpMinkowski problem for polytopes for 0＜p＜1[J].J.Funct.Anal.,2015,269(4):1070–1094.

[23]Zhu Guangxian.The LpMinkowski problem for polytopes for p＜0[J].Indiana Univ.Math.J.,arXiv:1602.07774..

[24]Zhu Guangxian.Continuity of the solution to the LpMinkowski problem[J].Proc.Am.Math.Soc.,2017,145(1):379–386.

[25]Bonnesen T,Fenchel W.Theory of convex bodies[M].HK:BCS Associates,1986.

[26]Alexandrov A D.Zur theorie der gemischten volumina von konvexen korpern III[J].Mat.Sb.,1938,3(2746):2.

[27]Fenchel W,Jessen B.Mengenfunktionen und konvexe Körper[M].København:Levin og Munksgaard,1938.

[28]Lewy H.On differential geometry in the large,I(Minkowski’s problem)[J].Trans.Amer.Math.Soc.,1938,43(2):258–270.

[29]Nirenberg L.The Weyl and Minkowski problems in differential geometry in the large[J].Commun.Pure Appl.Math.,1953,6(3):337–394.

[30]Pogorelov A V.On existence of a convex surface with a given sum of the principal radii of curvature[J].Uspekhi Matematicheskikh Nauk,1953,8(3):127–130.

[31]Calabi E.Improper affine hyperspheres of convex type and a generalization of a theorem by K.Jörgens[J].Michigan Math.J.,1958,5(2):105–126.

[32]Cheng S Y,Yau S T.On the regularity of the solution of the n-dimensional Minkowski problem[J].Commun.Pure Appl.Math.,1976,29(5):495–516.

[33]Pogorelov A V.The multidimensional Minkowski problem[M].Washington:Winston,1978.

[34]Caffarelli L A.Interior W2,p-estimates for solutions of the Monge-Amp`ere equation[J].Ann.Math.,1990,131(1):135–150.

[35]Gardner R.The Brunn-Minkowski inequality[J].Bull.Amer.Math.Soc.,2002,39(3):355–405.

[36]Firey W J.p-means of convex bodies[J].Math.Scand.,1962,10:17–24.

[37]Firey W J.Shapes of worn stones[J].Math.,1974,21(1):1–11.

[38]Lu Jian,Wang Xujia.Rotationally symmetric solutions to the Lp-Minkowski problem[J].J.Diff.Equ.,2013,254(3):983–1005.

[39]Ivaki M N.A flow approach to the L−2Minkowski problem[J].Adv.Appl.Math.,2013,50(3):445–464.

[40]Tzitz´eica M G.Sur une nouvelle classe de surfaces[J].Rendiconti del Circolo Matematico di Palermo,1908,25(1):180–187.

[41]Leichtweiss K.On a problem of W.J.Firey in connection with the characterization of spheres[J].Math.Pannon.,1995,6(1):67–75.

[42]Petty C M.Affine isoperimetric problems[J].Ann.New York Acad.Sci.,1985,440(1):113–127.

[43]Chen Fangwei,Zhou Jiazu.Some inequalities on general dual mixed volumes[J].J.Math.,2010,30(3):473–479.

[44]Guan Pengfei,Ma Xinan,Trudinger N,Zhu Xiaohua.A form of Alexandrov-Fenchel inequality[J].Pure Appl.Math.Quart.,2010,4:999–1012.

[45]Hu Changqing,Ma Xinan,Shen Chunli.On the Christoffel-Minkowski problem of Firey’s p-sum[J].Cal.Var.Part.Diff.Equ.,2004,21(2):137–155.

[46]Guan Pengfei,Ma Xinan.The Christoffel-Minkowski problem I:convexity of solutions of a Hessian equation[J].Invent.math.,2003,151(3):553–577.

[47]Urbas J I E.An expansion of convex hypersurfaces[J].J.Diff.Geom.,1991,33(1):91–125.