A NEW PATH THEOREM AND A NEW ITERATIVE SCHEME FOR INFINITE M-ACCRETIVE OPERATORSAND COMPUTATIONAL EXPERIMENT

WEI Li,ZHENG Ya-qin

(1.School of Mathematics and Statistics,Hebei University of Economics and Business,Shijiazhuang 050061,China)

(2.College of Science,Agricultural University of Hebei,Baoding 071001,China)

1　Introduction

In this paper,we assume that E is a real Banach space with E∗being its dual space.“→”denotes strong convergence and〈x,f〉denotes the value of f∈E∗at x∈E.

The normalized duality mapping J:E→2E∗is defined by

If E is uniformly smooth,then J is norm-to-norm uniformly continuous on each bounded subset in E[1].

(1)nonexpansive if

(2)contraction with coefficient k if there exists 0＜ k＜1 such that

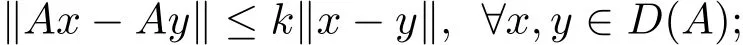
(3)accretive if for all x,y∈D(A),there exists j(x−y)∈J(x−y)such that

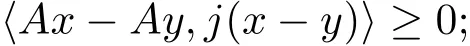
(4)m-accretive if A is accretive and R(I+λA)=E,∀λ＞ 0;

(5)strongly positive operator with coefficientwhere E is a real smooth Banach space and

In this case,

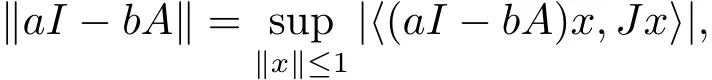
where I is the identity mapping,a∈ [0,1]and b∈ [−1,1];

(6)demiclosed at p if whenever{xn}is a sequence in D(A)such that xn⇀x∈D(A)and Axn→p then Ax=p,here‘⇀’denotes weak convergence in E.

If A is accretive,then we can define,for each r＞0,a single-valued mapping,which is called the resolvent of A[1].It is well knownis non-expansive and

Let C be a nonempty,closed and convex subset of E and Q be a mapping of E onto C.Then Q is said to be sunny[3]if Q(Q(x)+t(x−Q(x)))=Q(x)for all x∈E and t≥0.

A mapping Q of E into E is said to be a retraction[3]if Q2=Q.If a mapping Q is a retraction,then Q(z)=z for every z∈R(Q),where R(Q)is the range of Q.

A subset C of E is said to be a sunny nonexpansive retract of E[3]if there exists a sunny nonexpansive retraction of E onto C and it is called a nonexpansive retract of E if there exists a nonexpansive retraction of E onto C.

Finding the solution of the problem 0∈Aix(i∈N+)is one of hot topics in applied mathematics,where Aiis accretive,since the solutions correspond to the equilibrium points of some evolution systems.Based on this reason,we shall first prove a new path convergence theorem and then present a new semi-implicit iterative scheme for approximating the common zero of infinite m-accretive operators.Some new ideas and proof techniques can be found based on weaker restrictions than the recent works in[4–7].

Lemma 1.1[8]Assume F is a strongly positive bounded operator with coefficienton a real smooth Banach space E and 0＜ ρ≤ ‖F‖−1.Then

Lemma 1.2[1]Let E be a Banach space and C be a nonempty closed and convex subset of E.Let f:C→C be a contraction.Then f has a unique fixed point u∈C.

Lemma 1.3[9]Let E be a real uniformly convex Banach space,C be a nonempty closed and convex subset of E and B:C→E be a nonexpansive mapping such that Fix(B)/=∅,then I−B is demiclosed at zero.

Lemma 1.4[10]Let E be a real strictly convex Banach space and C be its nonempty closed and convex subset.Let Bm:C→C be a nonexpansive mapping for each m≥1.Let{am}be a real number sequence in(0,1)such thatSuppose that ∅.Thenis nonexpansive with

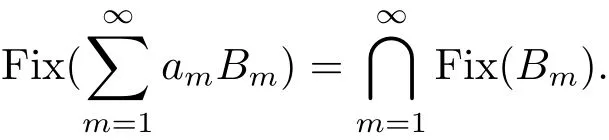
Lemma 1.5[11]In a real Banach space E,the following inequality holds

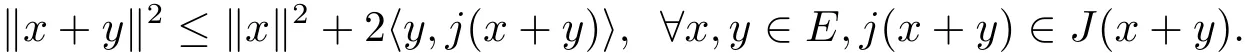
Lemma 1.6[6]Let r,t＞0.If E is uniformly convex,then there exists a continuous strictly increasing and convex function ϕ :R+→ R+with ϕ(0)=0 so that

for all x,y ∈ R(I+rA)with max{‖x‖,‖y‖} ≤ t,where A:E → E is m-accretive.

Lemma 1.7[12]Let{sn}be a real sequence that does not decrease at infinity,in the sense that there exists a subsequence{snk}so that snk≤snk+1for all k≥0.For every n ＞ n0,define an integer sequence{τ(n)}as

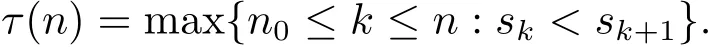
Then τ(n)→ ∞ as n → ∞ and for all n ＞ n0,max{sτ(n),sn} ≤ sτ(n)+1.

2　A New Path Theorem and a New Strong Convergence Theorem

Theorem 2.1Suppose E is a real uniformly smooth and uniformly convex Banach space,C is a nonempty,closed and convex sunny nonexpansive retract of E,and QCis the sunny nonexpansive retraction of E onto C.Let fi:E→E be a contractive mapping with coefficient k∈(0,1)and Fi:E → E be a strongly positive linear bounded operator with coefficientwhere i∈ N+.Let B:C → C be a nonexpansive mapping.Suppose{an}and{bn}are real number sequences in(0,1)withand Fix(B)/= ∅.If∀t∈ (0,1),define Wt:E → E by

then Wthas a fixed point xt,for eachwhich is convergent strongly to the fixed point of B,as t→0.That is,Moreover,p0is the unique solution of the following variational inequality:∀z∈ Fix(B),

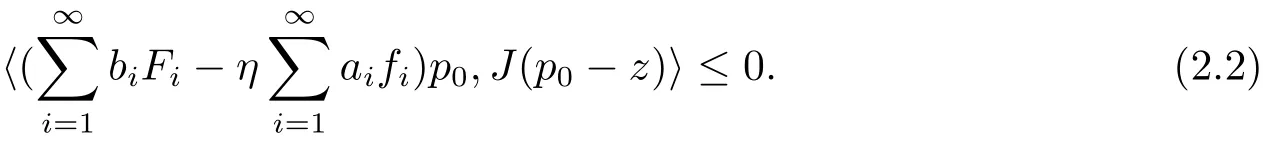
Proof Step 1is a strongly positive linear bounded operator with coefficient

It follows from the property of Fithat

Step 2Wtis a contraction for

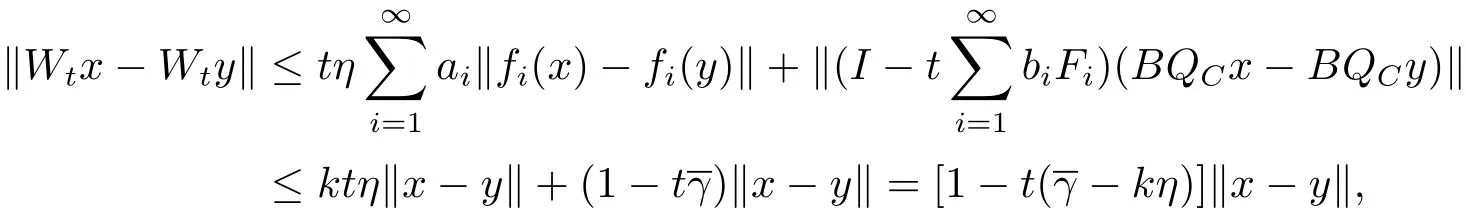
which implies that Wtis a contraction since.Then Lemma 1.2 implies that Wthas a unique fixed point,denoted by xt,which uniquely solves the fixed point equation

Step 3{xt}is bounded for tFor p ∈ Fix(B) ⊂ C,we have p=BQCp,then

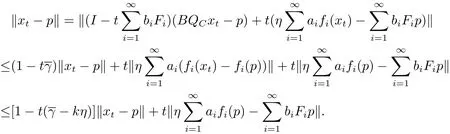
This ensures that

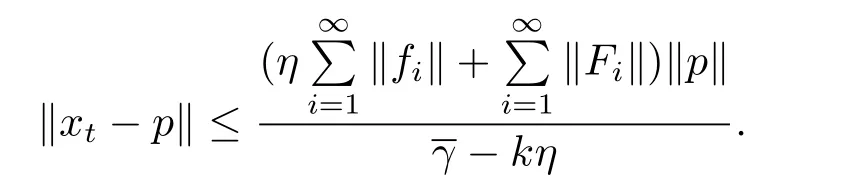
Thus{xt}is bounded,and then bothandare bounded.

Step 4xt−BQCxt→0,as t→0.From Step 3,we have

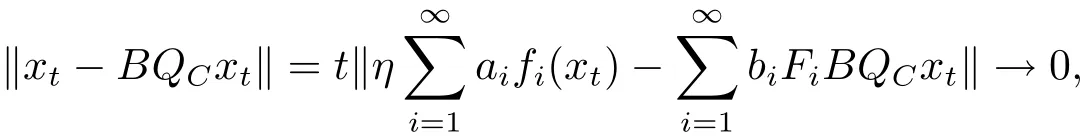
as t→0.

Step 5If variational inequality(2.2)has solutions,the solution must be unique.

Suppose both u0∈Fix(B)and v0∈Fix(B)are the solutions of the variational inequality(2.2).Then we have

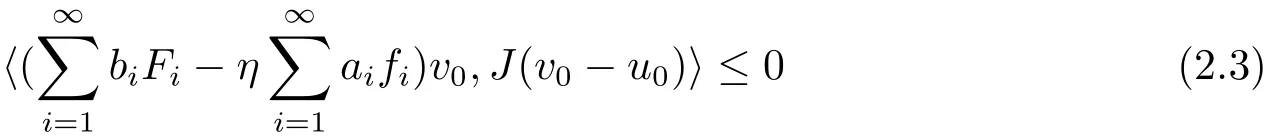
and

Adding up(2.3)and(2.4),we obtain that

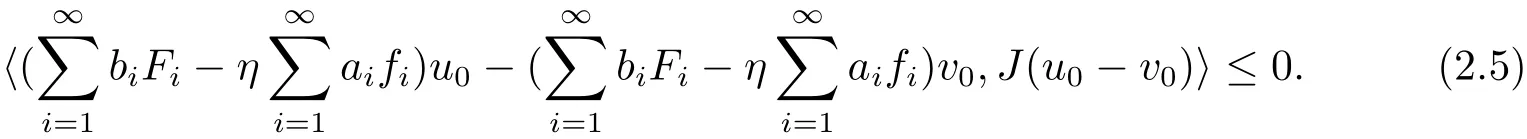
Since

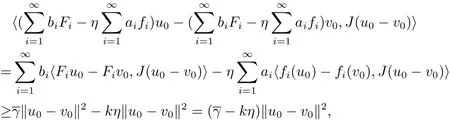
then(2.5)implies that u0=v0.

Step 6xt→p0∈Fix(B),as t→0,which satisfies the variational inequality(2.2).

Assume tn→0.Set xn:=xtnand defined µ:E →R by µ(x)=LIM‖xn−x‖2,x∈E,where LIM is the Banach limit on l∞.Let

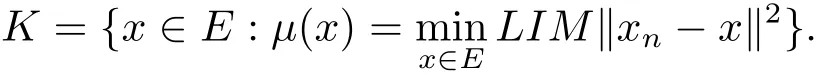
It is easily seen that K is a nonempty closed convex bounded subset of E.Since xn−BQCxn→0,then for x∈K,

it follows that BQC(K)⊂K;that is,K is invariant under BQC.Since a uniformly smooth Banach space has the fixed point property for nonexpansive mappings,BQChas a fixed point,say p0,in K.That is,BQCp0=p0∈C which ensures that p0=Bp0from the definition of B and then p0∈Fix(B).Since p0is also a minimizer of µ over E,it follows that,for t∈(0,1),

Since E is uniformly smooth,then by letting t→0,we find the two limits above can be interchanged and obtain

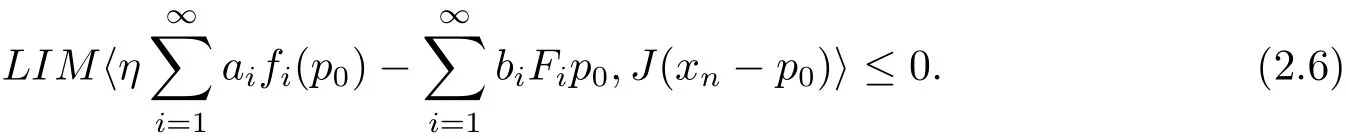
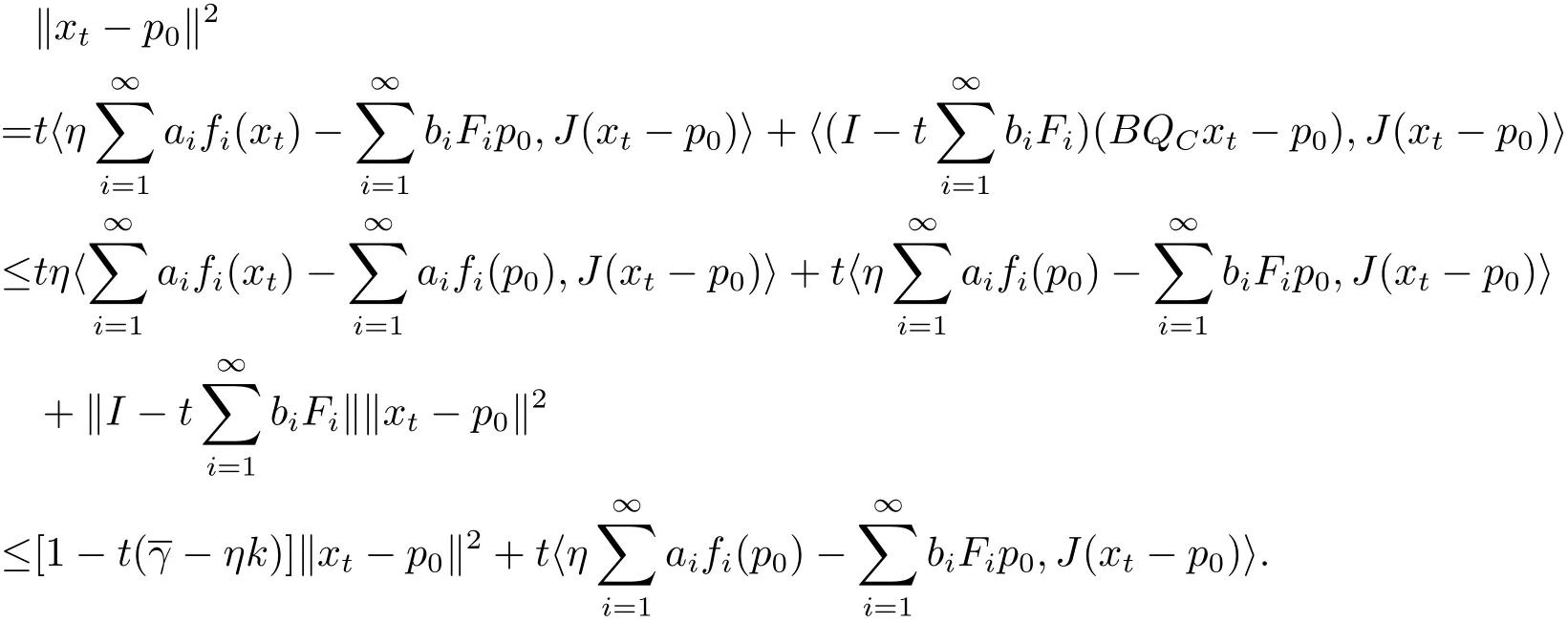
Therefore

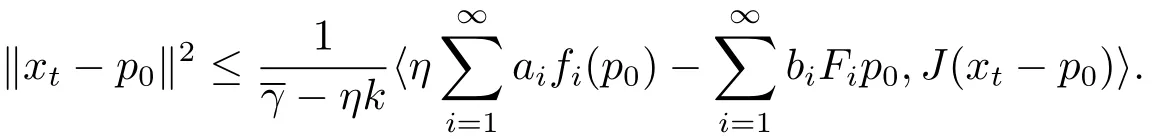
Hence by(2.6),

which implies that LIM‖xn− p0‖2=0,and then there exists a subsequence which is still denoted by{xn}such that xn→p0.

Next,we shall show that p0solves the variational inequality(2.2).

∀z∈ Fix(B),we have

Taking the limits on both sides of the above inequality,

since xn→p0and J is uniformly continuous on each bounded subsets of E.

Thus p0satisfies the variational inequality(2.2).

Now assume there exists another subsequence{xm}of{xt}satisfying xm→q0.Then Step 4 implies that BQCxm→q0.From Lemma 1.3,we know that I−BQCis demiclosed at zero,then q0=BQCq0which ensures that q0∈Fix(B).Repeating the above proof,we can also know that q0solves variational inequality(2.2).Thus p0=q0in view of Step 5.

Hence xt→p0,as t→0,which is the unique solution of the variational inequality(2.2).

This completes the proof.

Theorem 2.2Let E,C,QC,fi,Fi,k andbe the same as those in Theorem 2.1,and let Ai:C → C be m-accretive operator for i ∈ N+.Let{αn},{δn},{βn},{ζn},{γn},{an},{bn}and{cn}be real number sequences in(0,1)with.Letfor i∈ N+,E and.Suppose

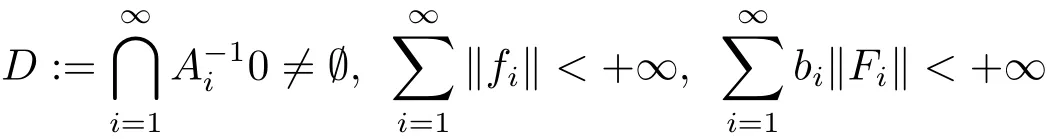
Let{xn}be generated by the following iterative scheme

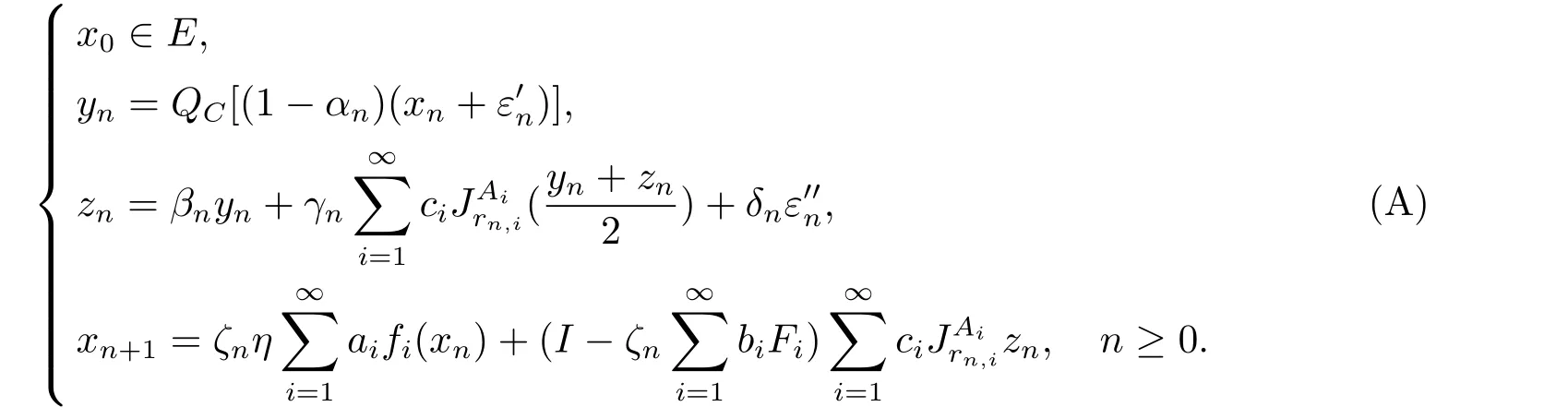
Then{xn}converges strongly to the unique element p0∈D,which satisfies the following variational inequality:∀z∈D,

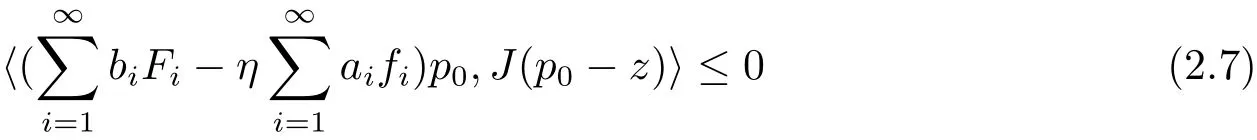
under the assumptions that

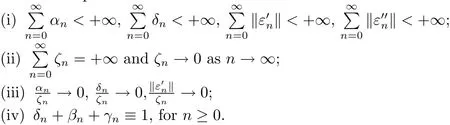
ProofWe shall split the proof into five steps.

Step 1{xn}is well-defined.

In fact,it suffices to show that{zn}is well-defined.

For t,s∈(0,1),define Ut,s:C→C bywhere B:C→C is nonexpansive and x,u,v∈C.Then

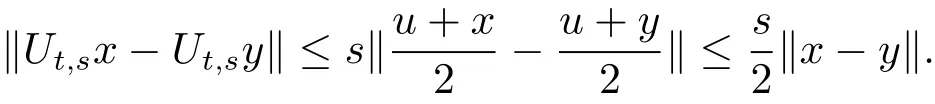
Thus Ut,sis a contraction,which ensures from Lemma 1.2 that there exists xt,s∈C such that Ut,sxt,s=xt,s.That is,

Step 2{xn},{yn}and{zn}are all bounded.

∀p∈D,we see that for n≥0,

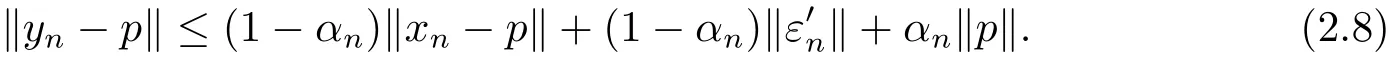
Therefore for p∈D and n≥0,we have

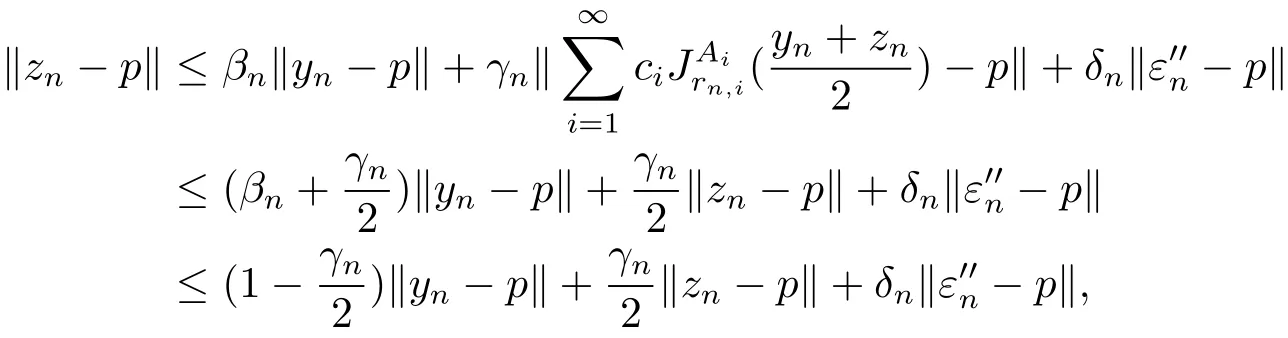
which implies that

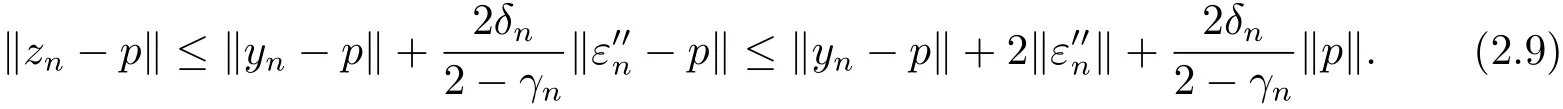
Using Lemma 1.1,(2.8)and(2.9),we have for n≥0,

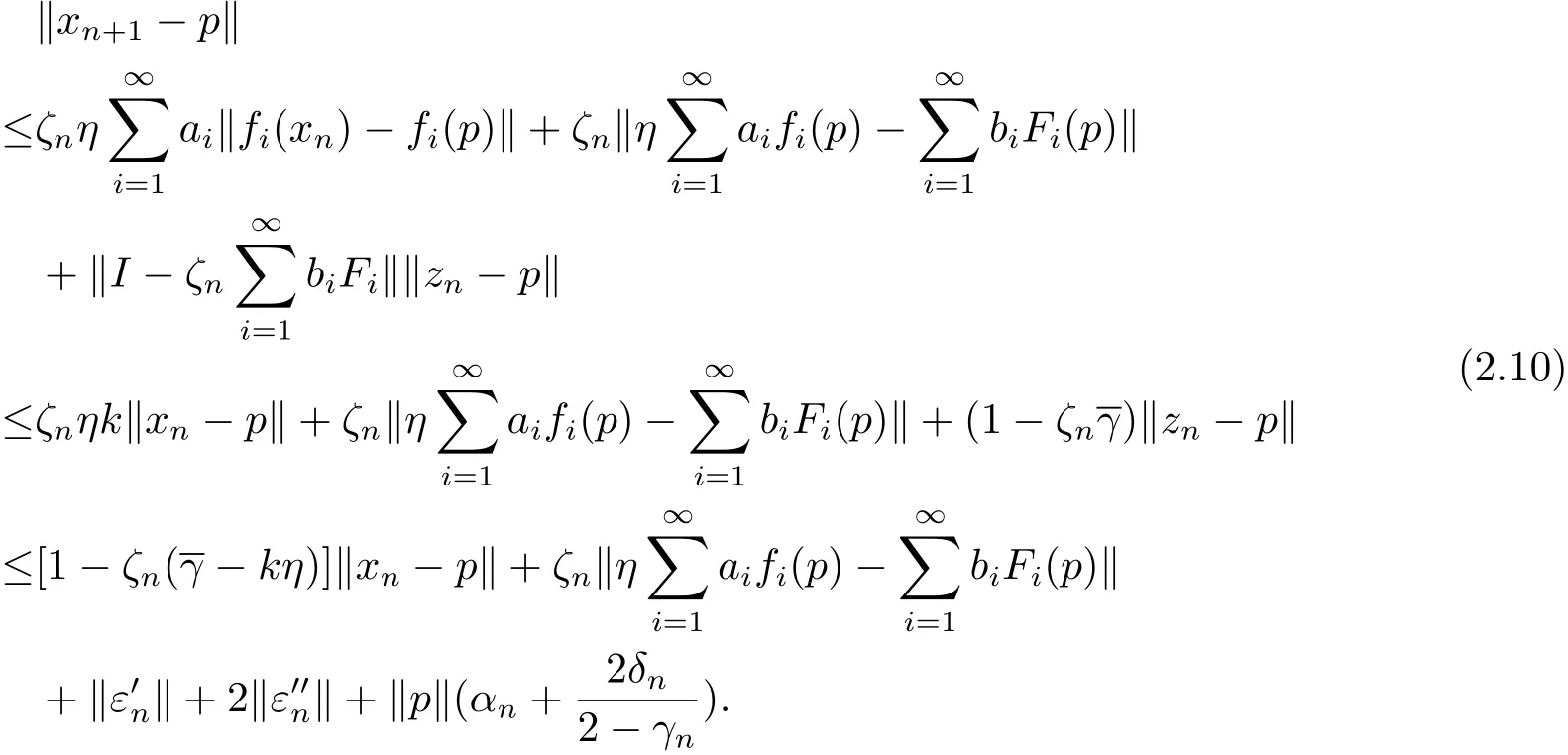
By using the inductive method,we can easily get the following result from(2.10)

Therefore from assumption(i),we know that{xn}is bounded.Setn≥0}.Then M is a positive constant.

Step 3

Step 4

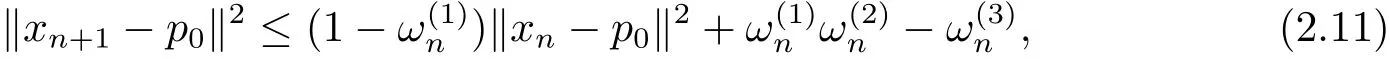
where p0is the unique solution of variational inequality(2.7),M′=4M+2‖p0‖,

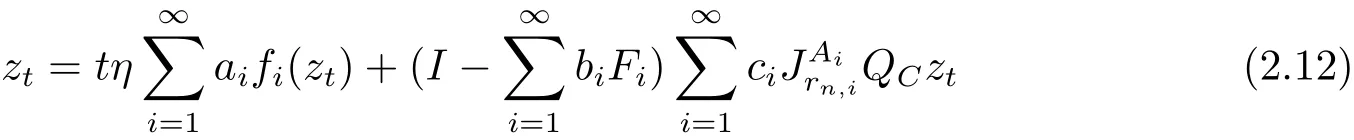
For this p0∈D,using Lemma 1.5,we have

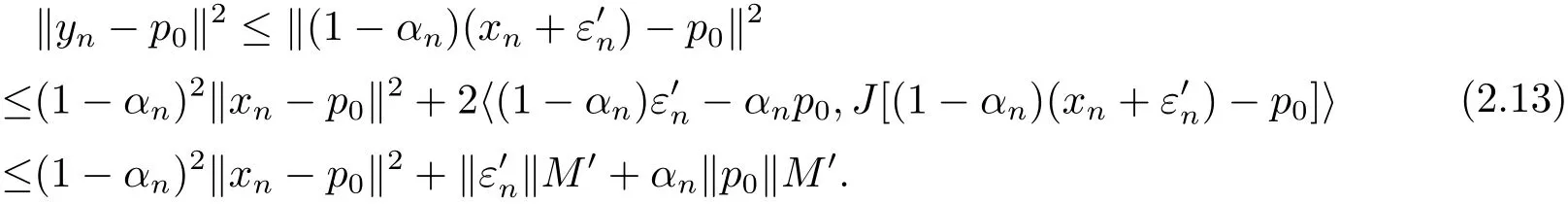
And using Lemma 1.6,

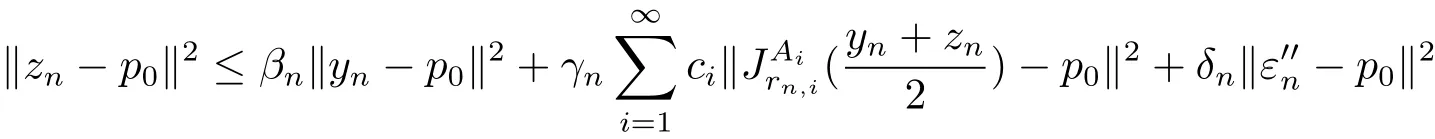
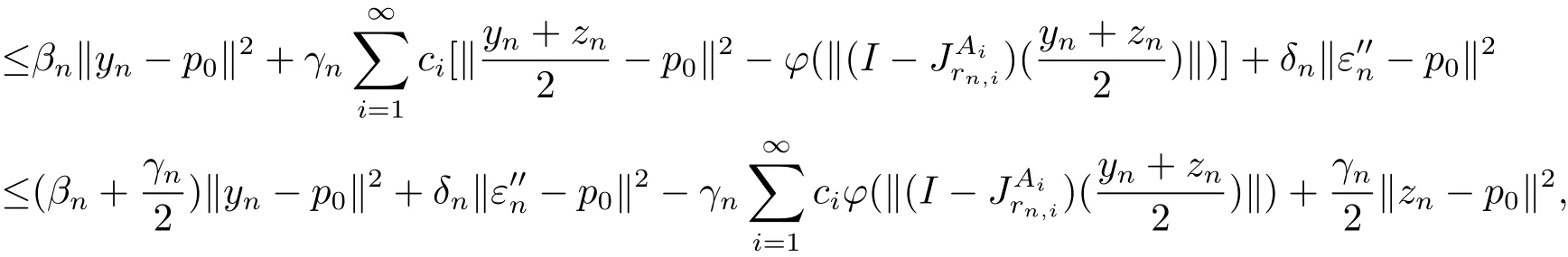
which implies that

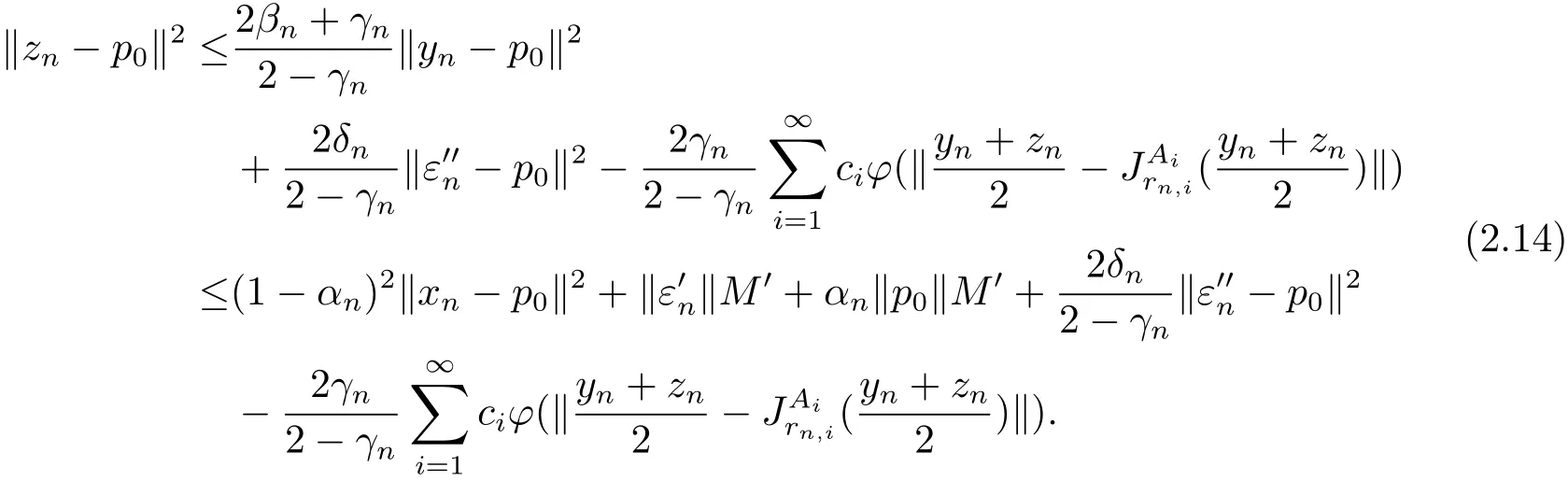
Now,noticing Step 1 in Theorem 2.1 and using Lemma 1.5 again,

Thus

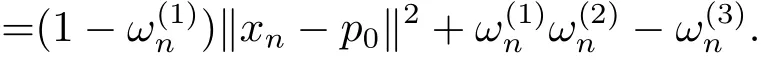
It follows from assumption(ii)that→ 0,as n→+∞.

Step 5xn→p0,as n→+∞,where p0is the same as that in Step 4.

Our next discussion will be divided into two cases:

Case 1{‖xn− p0‖}is decreasing.

If{‖xn−p0‖}is decreasing,we know from the result of Step 4 that

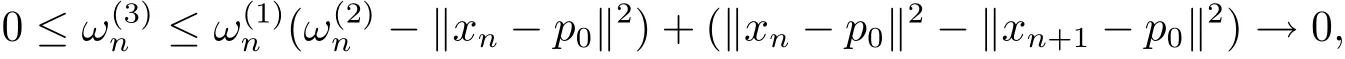
which ensures that

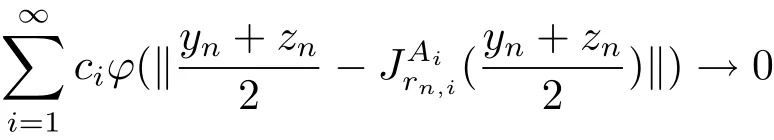
as n → +∞.Then from the property of ϕ,we know that

as n→+∞.Since

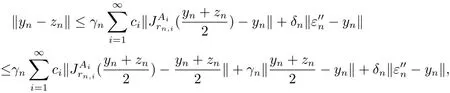
then

as n→+∞.Therefore

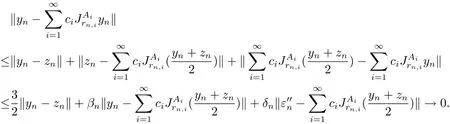
Next,we shall show that

Let ztbe the same as that in(2.12).Since ‖zt‖ ≤ ‖zt−p0‖+‖p0‖,then{zt}is bounded,as t→0.Using Lemma 1.5,we have

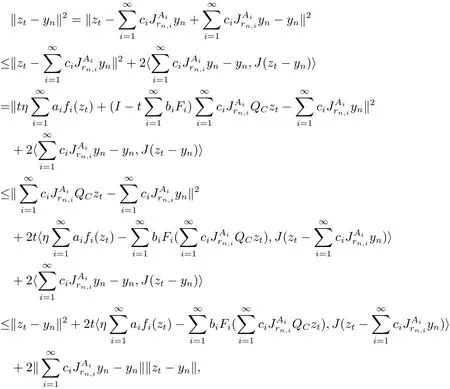
which implies that

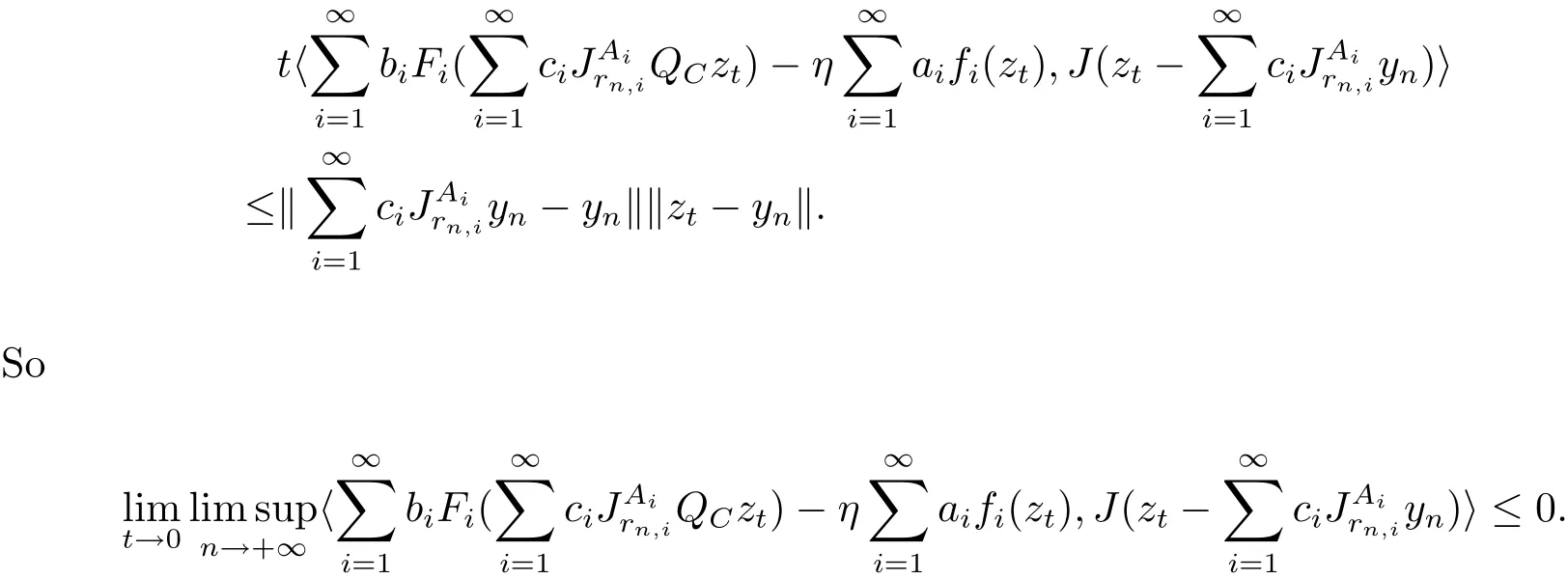
Since zt→p0,then

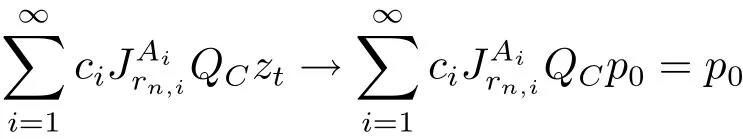
as t→0.Noticing that

then we have

Since yn−zn→0,thenwhich implies that Assumption(ii)and(2.15)ensure that

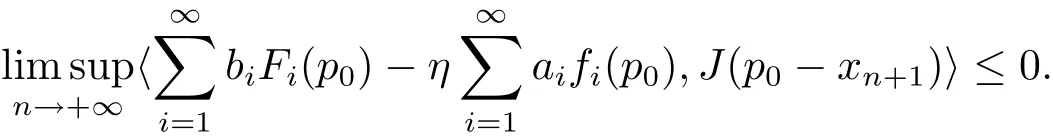
Employing(2.11)again,we have

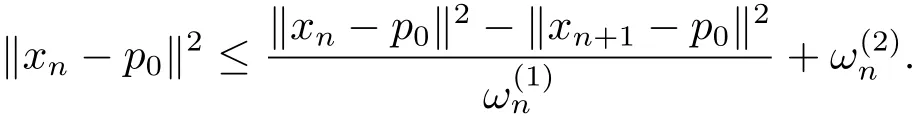
Assumption(ii)implies that lThen

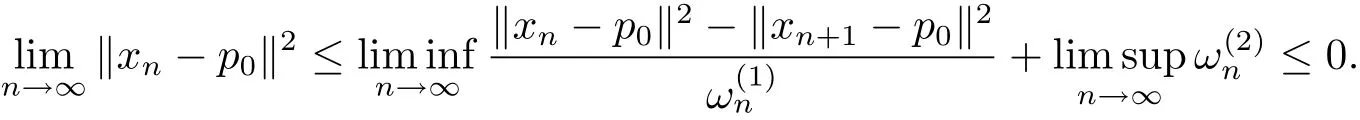
Then the result that xn→p0follows.

Case 2If{‖xn− p0‖}is not eventually decreasing,then we can find a subsequence{‖xnm− p0‖}so that‖xnm− p0‖ ≤ ‖xnm+1− p0‖ for all m ≥ 1.From Lemma 1.7,we can define a subsequence{‖xτ(n)− p0‖}so that max{‖xτ(n)− p0‖,‖xn− p0‖} ≤ ‖xτ(n)+1− p0‖for all n＞n1.This enable us to deduce that(similar to Case 1)

and then copy Case 1,we haveThusas n→∞.This completes the proof.

Remark 2.1In similar studies,e.g.[5],they usually have the following strong restrictions on the parameters:and γn+1−γn→ 0.By using new tools of Lemmas 1.6 and 1.7,these strong restrictions are deleted in our paper.

Remark 2.2In scheme(A),let E=C=(−∞,+∞),(n+1)2iandfor i∈N+and n≥0.Then all of the assumptions in Theorem 2.2 are satisfied and D={0}.By using Visual Basic six,we get Table 2.1 and Figure 2.1 below,from which we can see the convergence of{xn}.

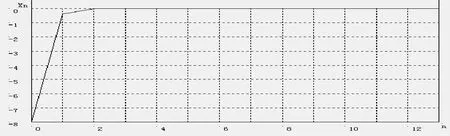
Figure 2.1:Convergence of{xn}

Table 2.1:Numerical Results of{xn}with Initial x0=−8.0

[1]Agarwal R P,O’Regan D,Sahu D R.Fixed point theory for Lipschitz-type mappings with applications[M].Germany:Springer-Verlag,2009.

[2]Cai Gang,Bu Shangquan.Approximation of common fixed points of a countable family of continuous pesudocontractions in a uniformly smooth Banach space[J].Appl.Math.Lett.,2001,24(2):1998–2004.

[3]Takahashi W.Proximal point algorithms and four resolvents of nonlinear operators of monotone type in Banach spaces[J].Taiwan.J.Math.,2008,12(8),1883–1910.

[4]Wei Li,Liu Yuanxing.Strong and weak convergence theorems for zeros of m−d-accretive mappings in Banach spaces[J].J.Math.,2016,36(3):573–583.

[5]Wei Li,Tan Ruilin.Iterative scheme with errors for common zeros of finite accretive mappings and nonlinear elliptic systems[J].Abstr.Appl.Anal.,2014,Article ID 646843,9 pages.

[6]Cui Huanhuan,Su Menglong.On sufficient conditions ensuring the norm convergence of an iterative sequence to zeros of accretive operators[J].Appl.Math.Comput.,2015,258:67–71.

[7]Wei Li,Agarwal R P.Iterative algorithms for in finite accretive mappings and applications to p-Laplacian-like differential systems[J].Fixed Point The.Appl.,2016,5:1–23.

[8]Cai Gang,Hu Changsong.Strong convergence theorems of a general iterative process for a finite family of λi-strictly pseudo-contractions in q-uniformly smooth Banach space[J].Comput.Math.Appl.,2010,59:149–160.

[9]Browder F E.Semicontractive and semiaccretive mappings in Banach spaces[J].Bill.Am.Math.Soc.,1968,74:660–665.

[10]Bruck R E.Properties of fixed-point sets of nonexpansive mappings in Banach spaces[J].Trans.Am.Math.Soc.,1973,179:251–262.

[11]Ceng Luchuan,Khan A R,Ansari Q H,Yao J C.Strong convergence of composite iterative schemes for zeros of m-accretive operators in Banach spaces[J].Nonlinear Anal.,2009,70:1830–1840.

[12]Maing P E.Strong convergence of projected subgradient methods for nonsmooth and nonstrictly convex minimization[J].Set-Valued Anal.,2008,66:899–912.