RIGIDITY THEOREMS OF THE SPACE-LIKE λ-HYPERSURFACES IN THE LORENTZIAN SPACE R

LI Xing-xiao,CHANG Xiu-fen

(School of Mathematics and Science Information,Henan Normal University,Xinxiang 453007,China)

1　Introduction

Let M be an immersed space-like hypersurface inof which the induced metric g is positive definite and x:be the corresponding immersion of M.In this paper,we also use x to denote the position vector of M.Thus x and the unit normal vector N are taken as smooth Rn+1-valued functions on Mn.For a suitably chosen function s on Mn,if the position vector x and the mean curvature H of M satisfy

then M is called a λ-hypersurface with the weight function s.

When s ≡ 0,the corresponding λ-hypersurfaces reduce to hypersurfaces with constant mean curvature which have been studied extensively.For example,Calabi considered in[1]the maximal space-like hypersurfaces Mnin the Lorentzian spaceand proposed some Bernstein-type problems for a nonlinear equation;for a given complete space-like hypersurface Mninwith constant mean curvature,it was proved by Xin[24]that if the Gauss map image of Mnis inside a bounded subdomain of the hyperbolic n-space Hn,then Mnmust be a hyperplane.A similar result was also proved earlier in[22]with extra assumptions.In[3],Cao,Shen and Zhu further extended the result by showing that if the image of the Gauss map lies inside a horoball of Hn,Mnis necessarily a hyperplane.Later,Wu[23]generalized the above mentioned results and proved a more general Bernstein theorem for complete space-like hypersurfaces in Lorentzian space with constant mean curvature.

If λ=0,then Mnis called a self-shrinker with weight s.In particular,if moreover s is chosen to be a constant,then Mnis nothing but the usual self-shrinker which play an important role in the study of the mean curvature flow because they describe all possible blow-ups at a given singularity of the mean curvature flow(see[5]or[8]with λ=0).Very recently,there have appeared some interesting results for space-like self-shrinkers.For example,after the submission of this paper,we were kindly informed the following results:Chen-Qiu[4]proved a rigidity(uniqueness)theorem that any complete m-dimensional spacelike self-shrinker in a pseudo-Euclidean spacemust be an affine plane,which is clearly a very important Bernstein-type result;Liu-Xin[19]obtained two rigidity theorems for closed(w.r.t the Euclidean topology)or complete space-like self-shrinkers Mminby using restrictions on the growth of either|H|2or the log of the w-function;and Ding-Wang[11]proved a Bernstein-type theorem for space-like graph self-shrinkers of higher codimension by assuming the sub-exponential decay of the metric determinant detg.As for the geometries of self-shrinkers in Euclidean space,a lot of interesting results were obtained in recent years,including some gap theorems and rigidity theorems.Details of this can be found in,for example,[2,7,10,12–14,16,18]etc.

According to[15],λ-hypersurfaces in the Euclidean space Rn+1were firstly studied by Mcgonagle and Ross in[20]withGuang[15]also studied the λ-hypersurfaces in Rn+1withand proved a Bernstein-type theorem showing that smooth λ-hypersuafaces which are entre graphs and with a polynomial volume growth are necessarily hyperplanes in Rn+1.

If one takes ε=s=1 in(1.1),the corresponding λ-hypersurfaces are exactly what Cheng and Wei defined and studied in[8],where the authors successfully introduced a weighted volume functional and proved that the λ-hypersuafaces in the Euclidean space Rn+1are nothing but the critical points of the above functional.Later,Cheng,Ogaza and Wei(see[6,9])obtained some rigidity and Bernstein-type theorems for these complete λ-hypersurfaces.In particular,the following result is proved.

Theorem 1.1[6]Let x:Mn→ Rn+1be an n-dimensional complete λ-hypersurface with weight s=−1 and a polynomial area growth.Then,either x is isometric to one of the following embedded hypersurfaces

1.the sphere Sn(r)⊂Rn+1with radius r＞0;

2.the hyperplane Rn⊂Rn+1;

3.the cylinder S1(r)×Rn−1⊂ Rn+1;

4.the cylinder Sn−1(r)×R ⊂ Rn+1,

or,there exists some p∈Mnsuch that the squared norm S of the second fundamental form of x satisfies

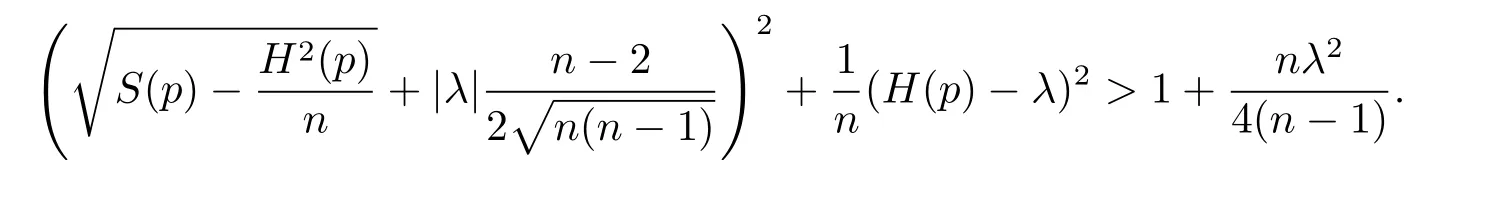
In this paper,we consider space-like λ-hypersurfaces x:in the Lorentzian spaceAfter extending the definitions of λ-hypersurfaces,we generalize the L-operator that has been effectively used by many authors(see the operatorsand L defined,respectively in(2.4)and(2.14)).We shall use these generalized operators to extend Theorem 1.1 to the complete space-like λ-hypersurfaces in

Let a be a nonzero constant and denote ∈=Sgn(a〈x,x〉),where 〈·,·〉is the Lorentzian product.We shall study λ-hypersurfaces ineither with weight s= ∈a when 〈x,x〉/=0,or with weight s= 〈x,x〉.Not that,in the first case,we can always choose an a such that a〈x,x〉＞ 0 implying ∈=1.

Now for a given hypersurface Mn,let S denote the squared norm of the second fundamental form,and A,I denote the shape operator and the identity map,respectively.Then the rigidity theorems we prove in this paper are stated as follows.

Theorem 1.2Let x:be a complete space-like λ-hypersurface with weight s= ∈a and 〈x,x〉/=0,where a is a constant,such that

in which the differential operator L is defined by(2.4).Then,either x is totally umbilical and thus isometric to one of the following two hypersurfaces:

or,there exists some p∈Mnsuch that,at p,

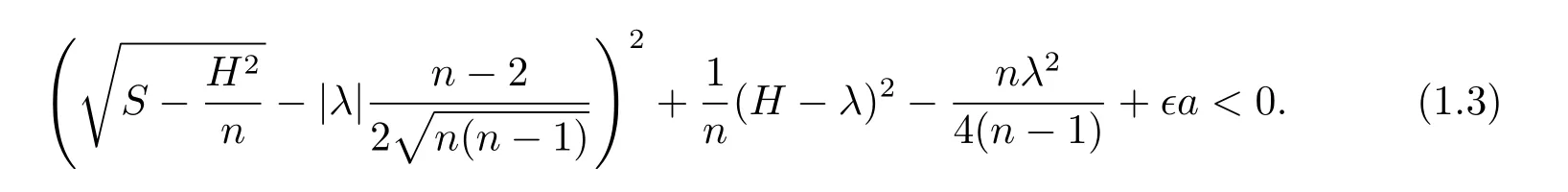
Remark 1.1Theorem 1.2 consists of two conclusions according to the two assumptions〈x,x〉＞ 0 and 〈x,x〉＜ 0.In the first case,we have ∈a ＞ 0.It follows that(1.3)always fails to true when λ=0.So we can obtain a Bernstein-type theorem for the usual space-like self-shrinkers which is unfortunately much weaker compared with that by Chen and Qiu in[4].This,on the other hand,motivates us that Theorem 1.2 can be further improved in general.For example,one may prove with great possibility an improvement of Theorem 1.2 by making applications of the idea and method that are used in[4].

Theorem 1.3Let x:be a complete space-like λ-hypersurface with weight s= 〈x,x〉.Suppose that

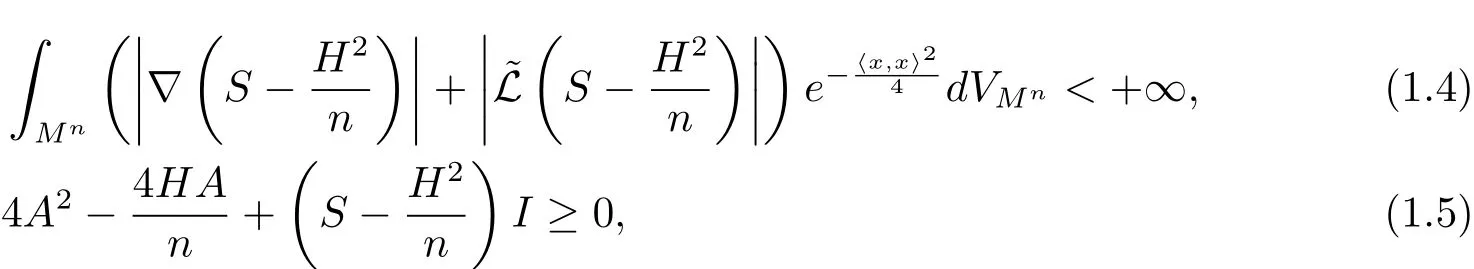
where the differential operatoris defined by(2.14).Then,either x is totally umbilical and thus isometric to one of the following two embedded hypersurfaces:

or,there exists some p∈Mnsuch that

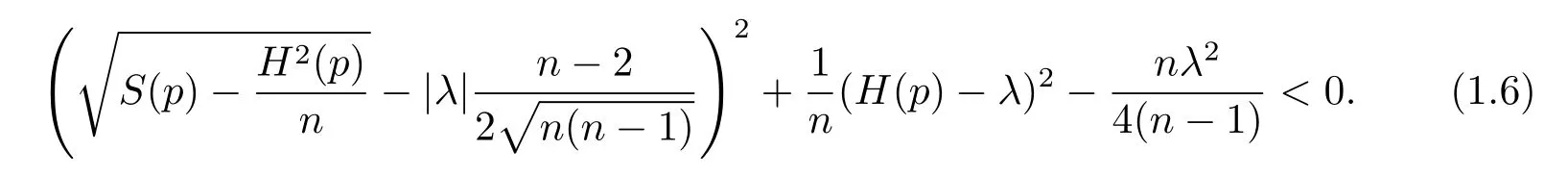
Theorems 1.2 and 1.3 will be proved in Section 3;Some necessary lemmas are given in Section 2.

As a direct corollary of Theorem 1.3,we obtain

Theorem 1.4Let x:be a complete space-like λ-hypersurface with weight s= 〈x,x〉.Suppose that(1.4)and(1.5)are satisfied.If

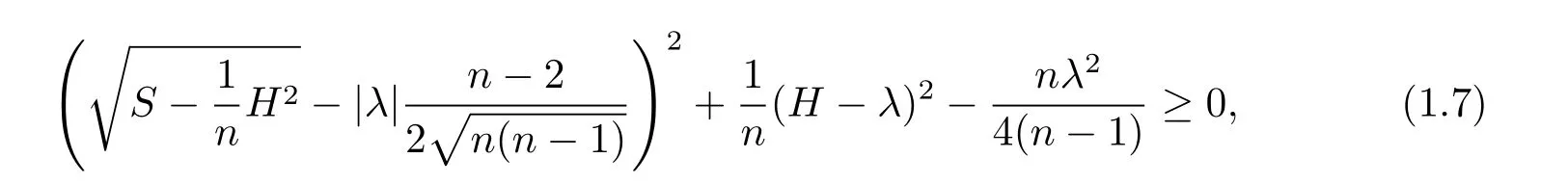
then one of the following two conclusions must hold:

2.λ=0 and x is isometric to the Euclidean space

ProofIf condition(1.7)is satisfied for a hypersurface Hn(−r−2)with r ＞ 0,then by the fact that x=rN,we haveIf follows that

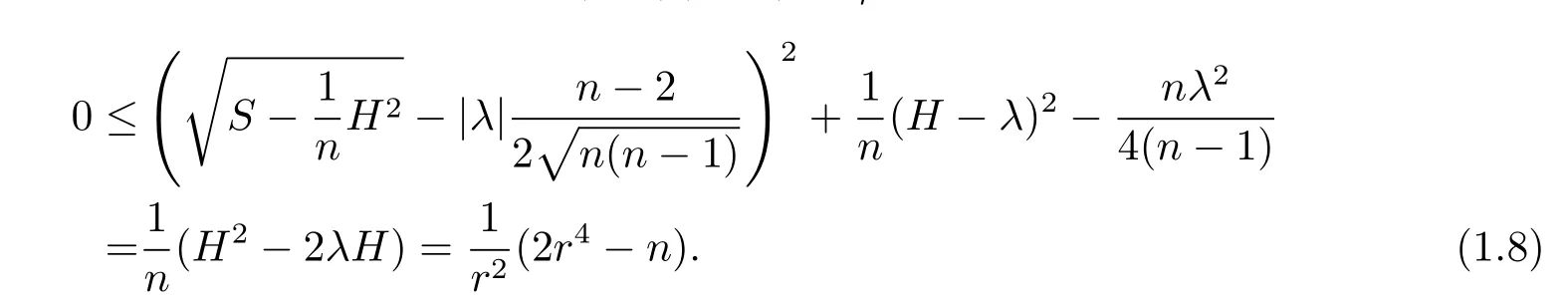
A similar corollary of Theorem 1.2 can also be derived,which is omitted here.

Corollary 1.5Let x:be a complete space-like λ-hypersurface with weight s= 〈x,x〉.Supposeis constant.If(1.5)and(1.7)are satisfied,then x is isometric to either the hyperbolic spaceor the hyperplane

ProofSinceis constant,condition(1.4)in Theorem 1.3 is trivially satisfied.Then Corollary 1.5 follows direct from Theorem 1.4.

Remark 1.2For the special case that λ =0,that is,for the case of “self-shrinker”with weight s,the following two conclusions can be easily seen from Theorem 1.4.

Theorem 1.6Let x:be a complete space-like self-shrinker with weight s= 〈x,x〉.Suppose that(1.4)and(1.5)are satisfied,then x is isometric to one of the following two embedded hypersurfaces:

ProofWhen λ=0,it is clear that(1.7)is trivially satisfied.Furthermore,for a hyperbolic spaceλ=0 also implies that

Corollary 1.7Let x:be a complete space-like self-shrinker with weight s= 〈x,x〉.Ifis con)stant and(1.5)is satisfied,then x is isometric to the either the hyperbolic space

ProofThe assumption thatis constant directly means that(1.4)is trivially satisfied.

2　Preliminaries and Lemmas

First,we fix the following convention for the ranges of indices or the hyperplane

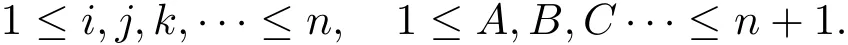
By restricting these forms to Mnand using Cartan’s lemma,we have

where hijare nothing but the components of the second fundamental form h of x,that is,Then the mean curvature H of x is given byDenote

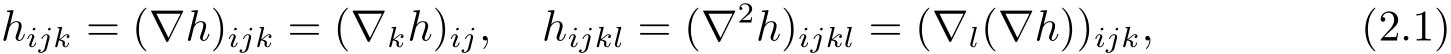
where▽is the Levi-Civita connection of the induced metric and▽i:=▽ei.Then the Gauss equations,Codazzi equations and Ricci identities are given respectively by

where Rijklare the components of the Riemannian curvature tensor.For a function F defined on Mn,the covariant derivatives of F are denoted by

Let∆ be the Laplacian operator of the induced metric on Mn.In case that〈x,x〉does not change its sign,we can define

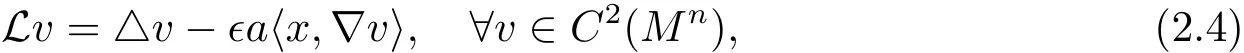
where,for any constant a,∈=Sgn(a〈x,x〉).Then L is an elliptic operator and

In fact,for v∈C2(Mn),we find

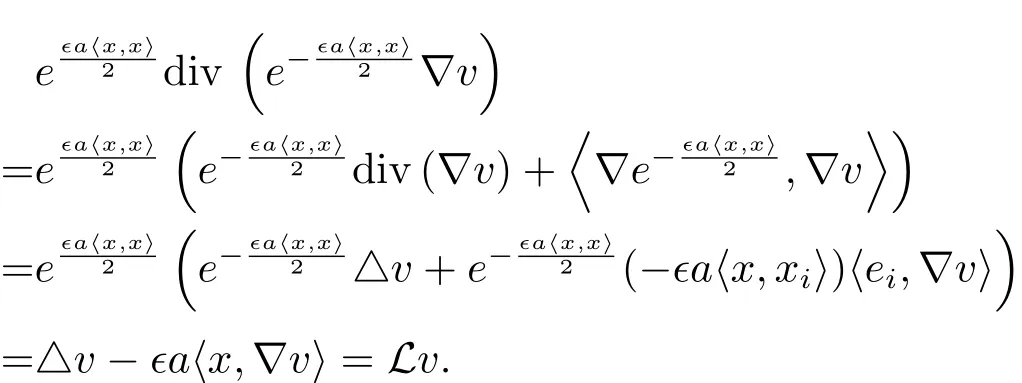
Lemma 2.1[5]Let x:be a complete space-like hypersurface for which〈x,x〉does not change its sign.Then,for any C1-function u on Mnwith compact support,it holds that

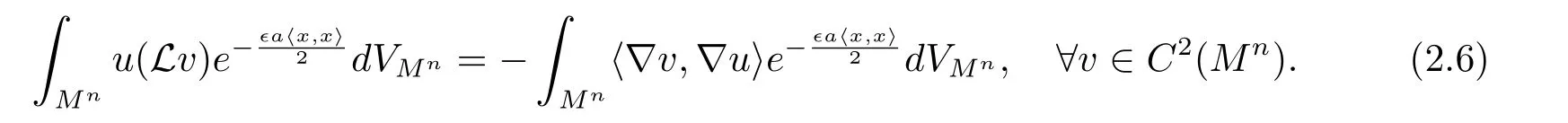
ProofBy(2.5),we find

Hence there are two cases to be considered:

Case(1)Mnis compact without boundary.In this case,we can directly use the divergence theorem to get

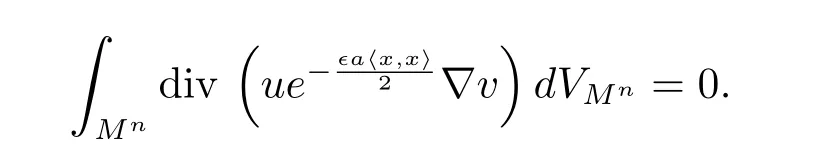
Case(2)Mnis complete and noncompact.In this case,we can find a geodesic ball Br(o)big enough such that Suppu⊂Br(o).It follows that

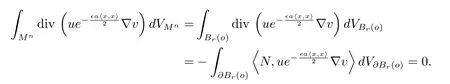
It follows that

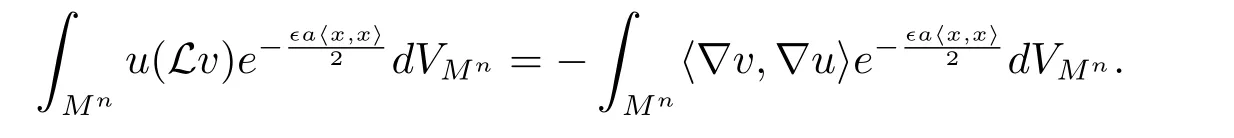
Corollary 2.2Let x:be a complete space-like hypersurface.If u,v are C2-functions satisfying

then we have

ProofWe will use square brackets[·]to denote weighted integrals

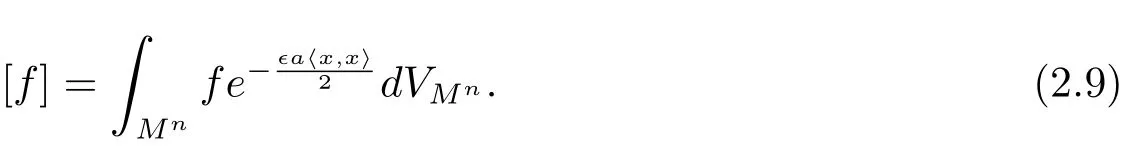
Given any φ that is C1-with compact support,we can apply Lemma 2.1 to φu and v to get

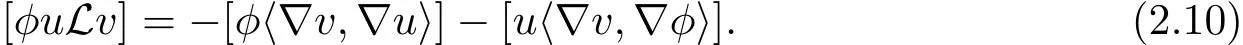
Now we fix one point o ∈ M and,for each j=1,2,···,let Bjbe the intrinsic ball of radius j in Mncentered at o.Define φjto be one smooth cutting-off function on Mnthat cuts off linearly from one to zero between Bjand Bj+1.Since|φj|and|▽φj|are bounded by one,φj→ 1 and|▽φj|→ 0,as j→ +∞.Then the dominated convergence theorem(which applies because of(2.7))shows that,as j→+∞,we have the following limits

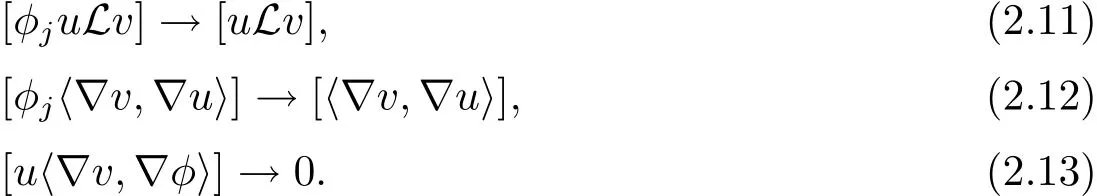
Replacing φ in(2.10)with φj,we obtain the corollary.

Next we consider the case that s= 〈x,x〉and define

Then similar to(2.5),we have for all v∈C2(Mn),

Lemma 2.3If x:is a complete space-like hypersurface,u is a C1-function with compact support,and v is a C2-function,then

ProofUsing(2.15),we have

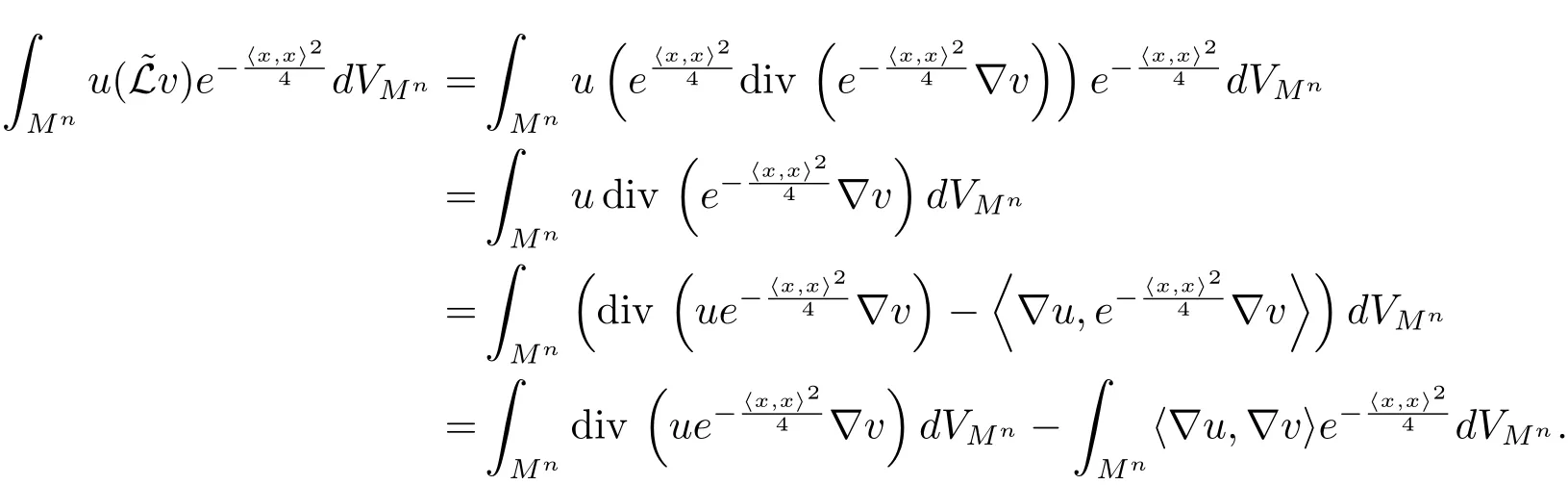
(1)If Mnis compact without boundary,then by the divergence theorem,

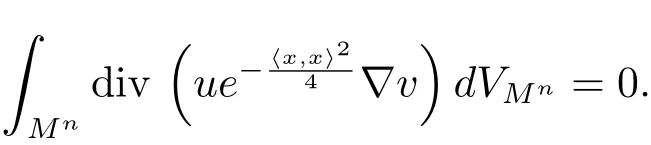
(2)If Mnis complete and noncompact,then there exists some geodesic ball Br(o)big enough such that Suppu⊂Br(o).It follows that

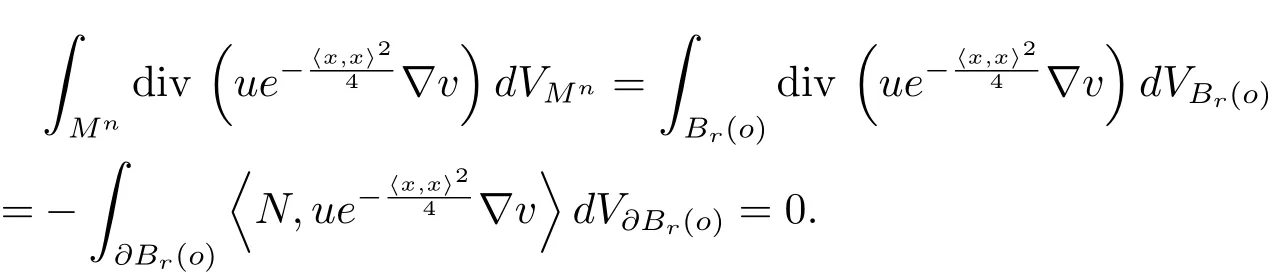
Therefore

Corollary 2.4Let x:be a complete space-like hypersurface.If u,v are C2-functions satisfying

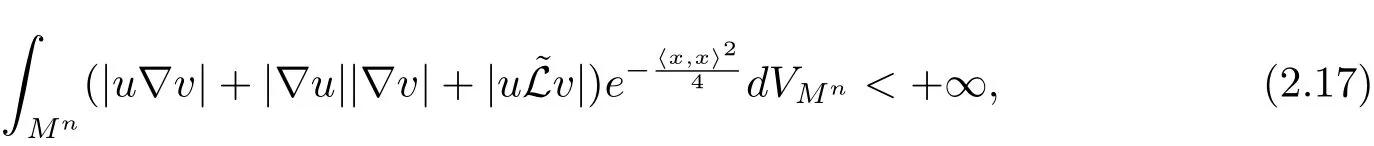
then we have

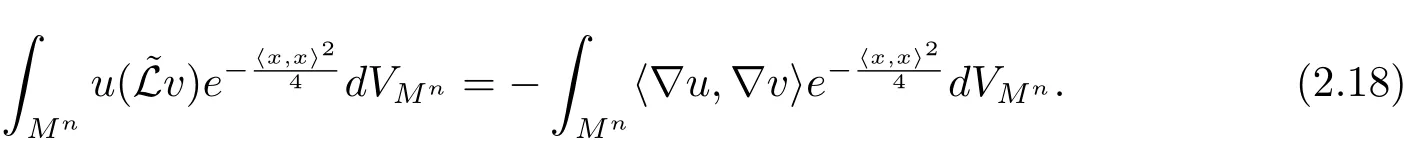
ProofThe proof is the same as that of Corollary 2.2 and is omitted.

The following lemma is also needed in this paper.

Lemma 2.5[21]Let µ1,···,µnbe real numbers satisfying

with β a nonnegative constant.Then

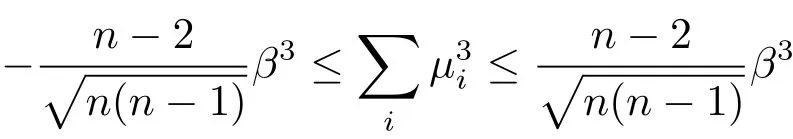
with either equality holds if and only if(n−1)of µiare equal to each other.

3　Proof of Main Theorems

3.1　Proof of Theorem 1.2

Since H − ∈a〈x,N〉= λ,we have

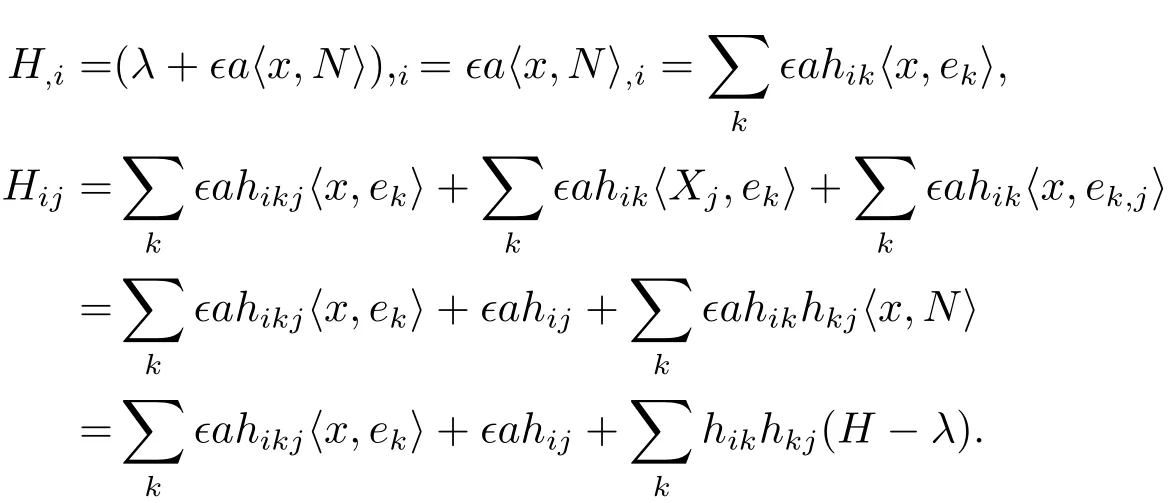
Using the Codazzi equation in(2.2),we infer

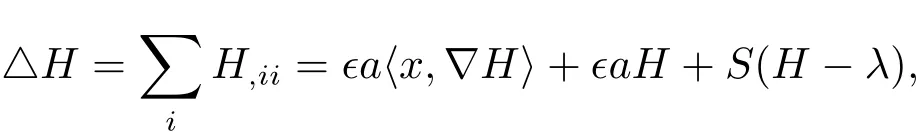
implying that

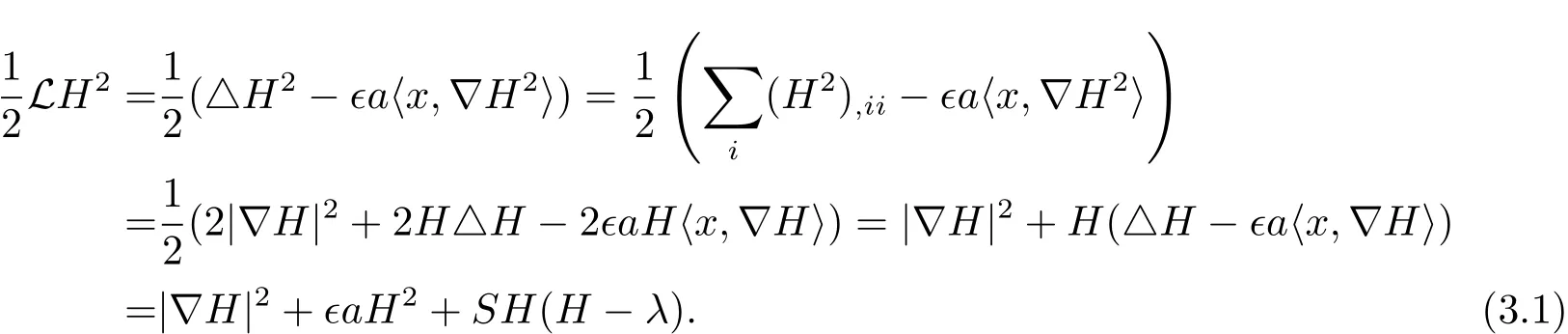
By making use of the Ricci identities and the Gauss-Codazzi equations,we have

Therefore it holds that

For any point p ∈ Mn,suitably choosing{e1,e2,···,en}around p such that hij(p)= λi(p)δij.Then at the given point p,

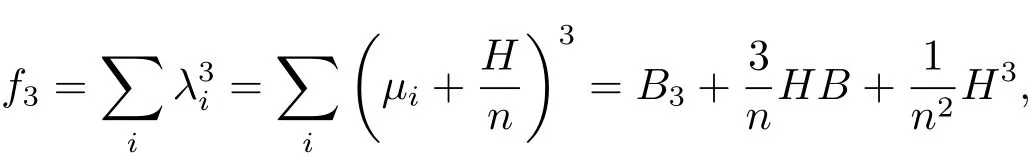
where

By a direct computation with(3.1)and(3.2),we have

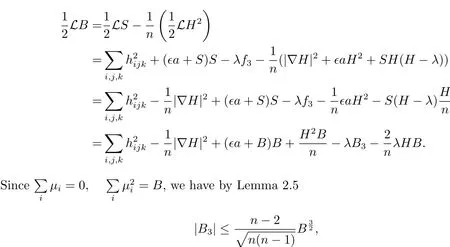
where the equality holds if and only if at least n−1 of µis are equal.Consequently,

Because of(1.2),we can apply Corollary 2.2 to functions 1 andto obtain

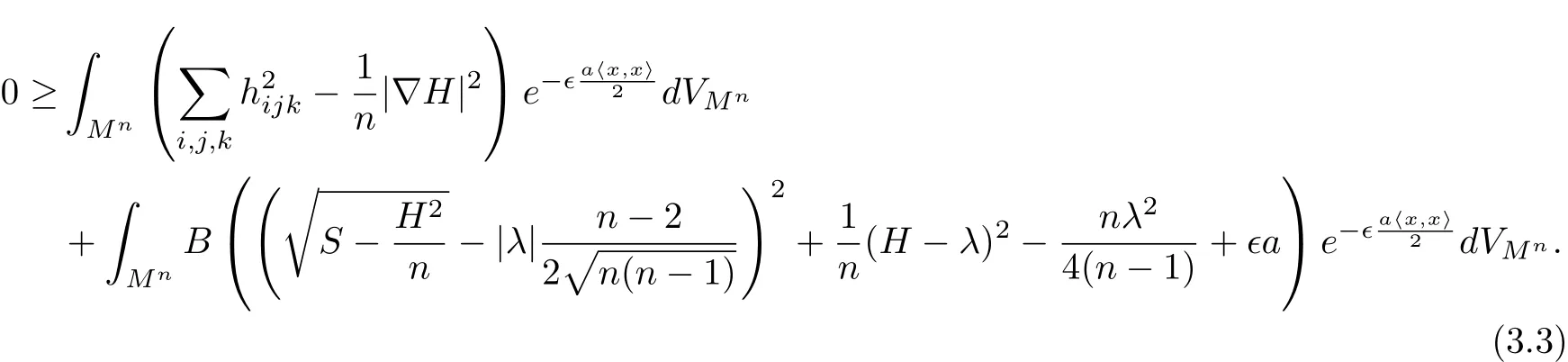
On the other hand,by use of the Codazzi equations and the Schwarz inequality,we find

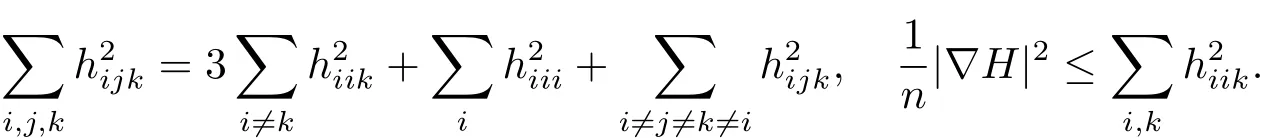
So that

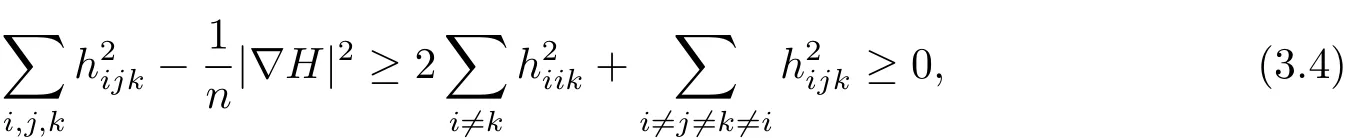
in which the equalities hold if and only if hijk=0 for any i,j,k.

If B/≡ 0 and,for all p ∈ Mn,(1.3)does not hold,that is

everywhere on Mn,then the right hand side of(3.3)is nonnegative.It then follows that

and

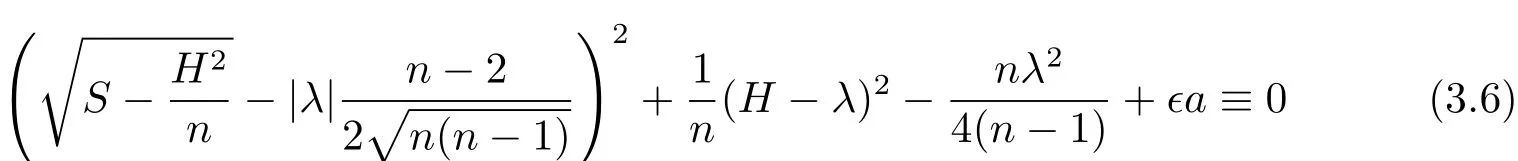
on where B/=0.By(3.4)and(3.5),the second fundamental form h of x is parallel.In particular,x is isoparametric and thus both B and H are constant.Since B/=0,the equality(3.6)shows that x is a complete isoparametric space-like hypersurface inof exactly two distinct principal curvatures one of which is simple.It then follows by[17]and B/=0 that x is isometric to one of the product spacesandBut it is clear that,for both of these two product spaces,the function 〈x,x〉does change its sign,contradicting the assumption.This contradiction proves that either B≡0,namely,x is totally umbilical and isometric to either of the hyperbolic n-spaceand the Euclidean n-spaceor there exists some p∈Mnsuch that(1.3)holds.

The proof of Theorem 1.2 is thus finished.

3.2　Proof of Theorem 1.3

Since the idea and method here are the same as those in the proof of Theorem 1.2,we omit the computation detail.

First,by H − 〈x,x〉〈x,N〉= λ,we have

Then by using the Codazzi equation in(2.2),we find

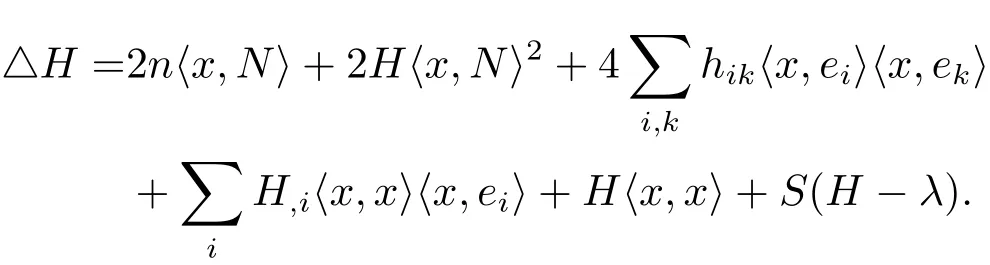
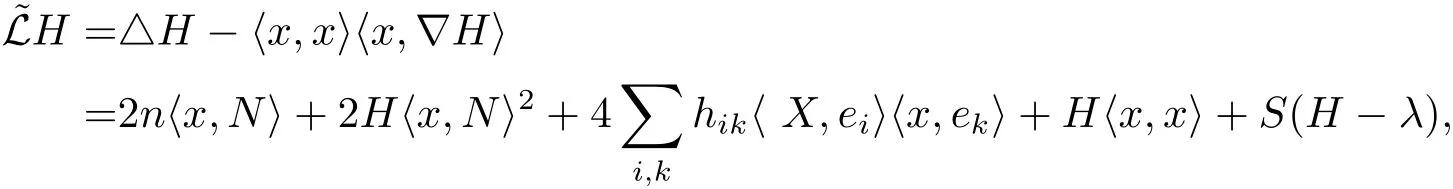
implying

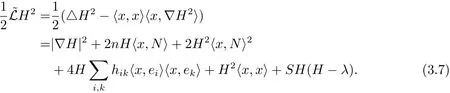
On the other hand,

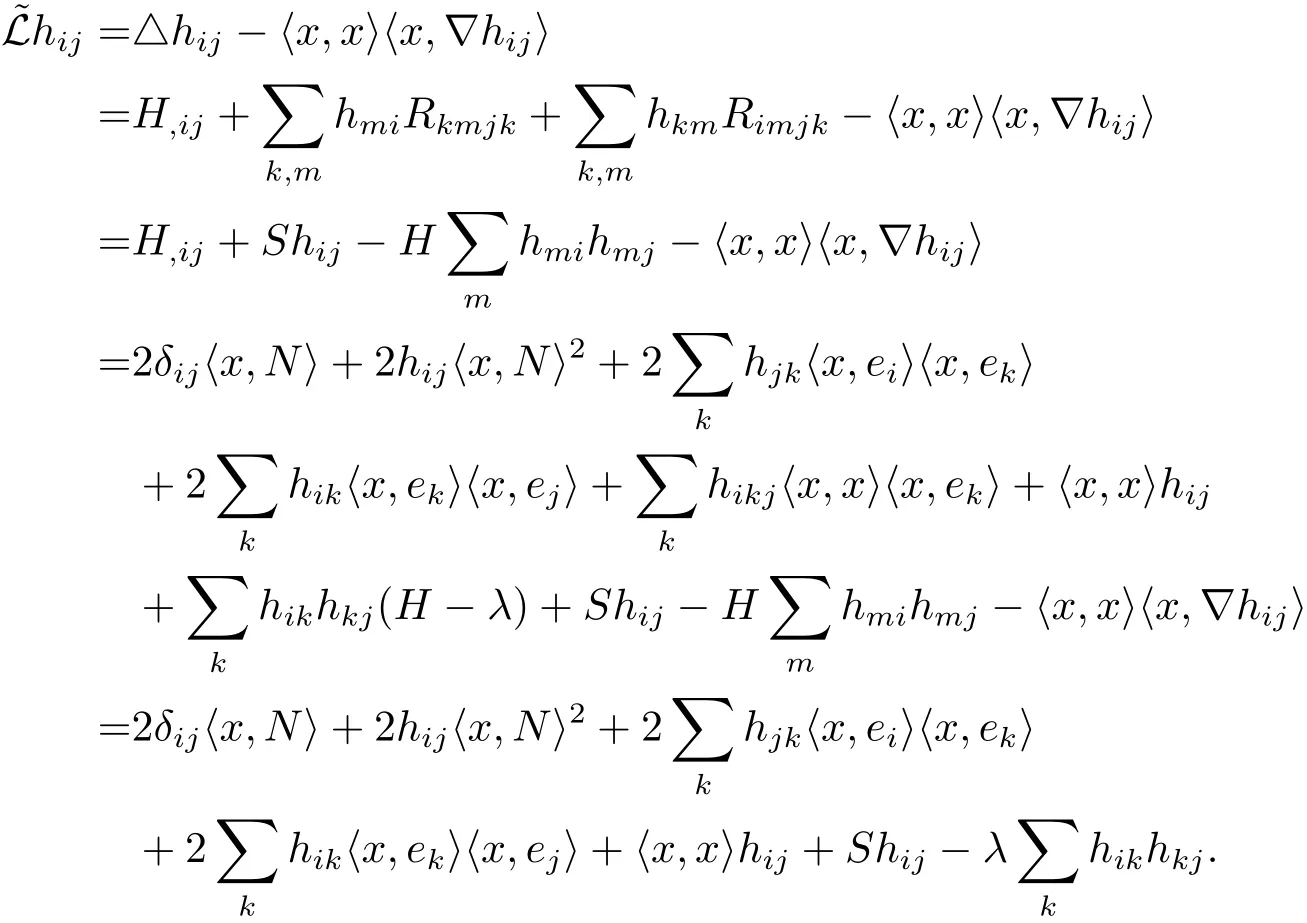
It follows that

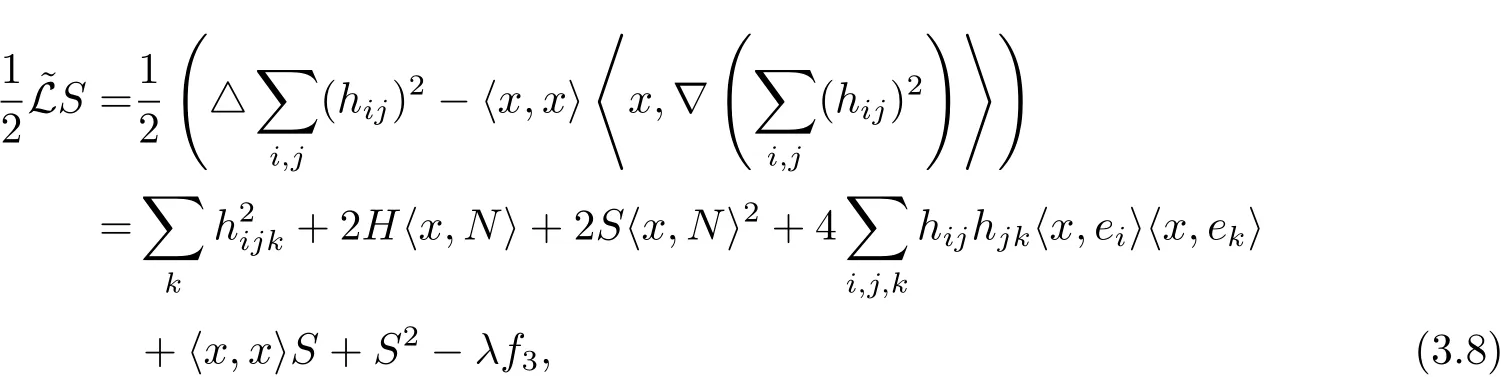
Denote by x┬= 〈x,ei〉eibe the tangential part of the position vector x.Then,as in the proof of Theorem 1.2,we can choose a suitable frame field{e1,e2,···,en}making diagonal the second fundamental form hijaround each point p∈Mn,and perform a direct computation using(1.5),(3.7)and(3.8)to obtain

where assumption(1.5)has been used.Once again we use Lemma 2.5 to get

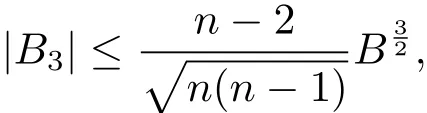
where the equality holds if and only if at least n−1 of µiare equal.It then follows that

Because of(1.4),we can apply Corollary 2.4 to functions 1 andto find

If B/≡ 0 and,for all p ∈ Mn,(1.6)does not hold,that is

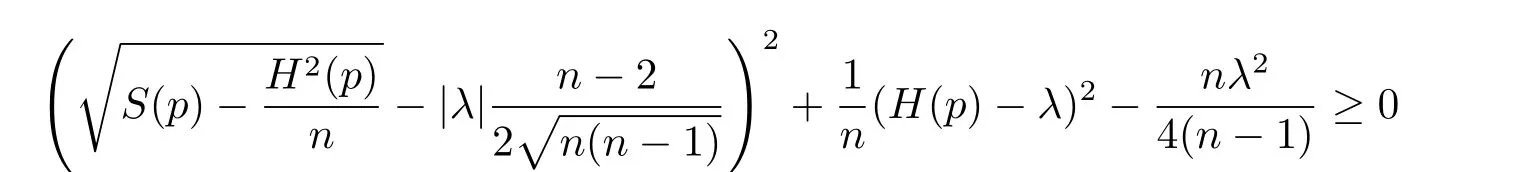
everywhere on Mn,then the right hand side of(3.10)is nonnegative.It then follows that

and at points where B/=0,

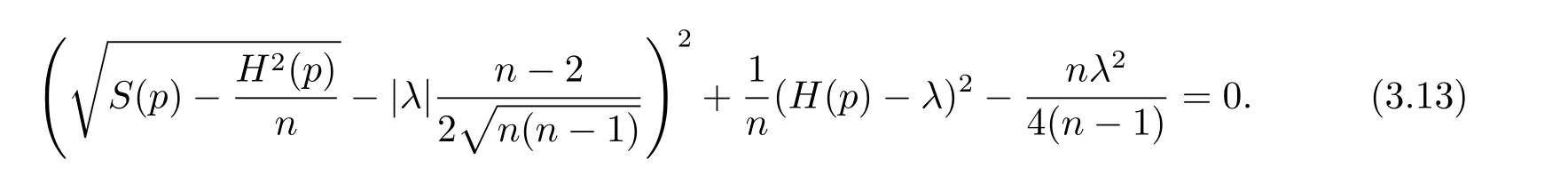
By(3.12)and(3.13),the second fundamental form h of x is parallel.In particular,x is isoparametric and thus both B and H are constant.Since B/=0,equality(3.6)shows that x is a complete isoparametric space-like hypersurface inof exactly two distinct principal curvatures one of which is simple.It then follows by[17]and B/=0 that x is isometric to one of the product spacesBut it is clear that,for both of these two product spaces,the function 〈x,x〉is not a constant so that bothandcould not be λ-hypersurfaces with s= 〈x,x〉.This contradiction proves that either B ≡ 0,namely,x is totally umbilical and isometric to either of the hyperbolic n-spaceand the Euclidean n-spaceor there exists some p∈Mnsuch that(1.6)holds.

The proof of Theorem 1.3 is thus finished.

[1]Calabi E.Examples of Bernstein problems for some nonlinear equations[J].Proc.Sym.Pure Appl.Math.,1968,15:223–230.

[2]Cao Huaidong,Li Haizhong.A gap theorem for self-shrinkers of the mean curvature flow in arbitrary codimension[J].Calc.Var.,2013,46:879–889.

[3]Cao Huaidong,Shen Ying,Zhu Shunhui.A Bernstein theorem for complete space-like constant mean curvature hypersurfaces in Minkowski space[J].Calc.Var.,1998,7:141–157.

[4]Chen Qun,Qiu Hongbin.Rigidity of self-shrinkers and translating solitons of mean curvature flows[J].Adv.Math.,2016,294:517–531.

[5]Colding T H,Minicozzi W P.Generic mean curvature flow I:generic singularities[J].Ann.Math.,2012,175(2):755–833.

[6]Cheng Qingming,Ogata S,Wei Guoxin.Rigidity theorems of λ-hypersurfaces[J].arXiv:1403.4123v2,1 Apr,2014.

[7]Cheng Qingming,Wei Guoxin.A gap theorem of self-shrinkers[J].arXiv:1212.6028v1,25 Dec,2012.

[8]Cheng Qingming,Wei Guoxin.Complete λ-hypersurfaces of weighted volume-preserving mean curvature flow[J].arXiv:1403.3177v3,10 Jun,2014.

[9]Cheng Qingming,Wei Guoxin.The Gauss image of λ-hypersurfaces,a Bernstein type problem[J].arXiv:1410.5302v1,20 Oct,2014.

[10]Cheng Qingming,Peng Yejuan.Complete self-shrinkers of the mean curvature flow[J].Calc.Var.,2015,52:497–506.

[11]Ding Qi,Wang Zhizhang.On the self-shrinking system in arbitrary codimensional spaces[J].arXiv:1012.0429v2,2010.

[12]Ding Qi,Xin Yuanlong.The rigidity theorems of self shrinkers[J].Trans.Amer.Math.Soc.,2014,366(10):5067–5085.

[13]Ding Qi,Xin Yuanlong,Yang Ling.The rigidity theorems of self shrinkers via Gauss maps[J].arXiv:1203.1096v1,6 Mar,2012.

[14]Guang Qiang.Self-shrinkers withsecondfundamental formof constant length[J].arXiv:1405.4230v1,16 May,2014.

[15]Guang Qiang.Gap and rigidity theorems of λ-hypersurfaces[J].arXiv:1405.4871v1,19 May,2014.

[16]Han Fangfang,Yang Dengyun.On spectral characterizations of self-shrinkers on Rn+1(in Chinese)[J].J.Math.,2014,34(5):1010–1015.

[17]Lawson H B.Local rigidity theorems for minimal hypersurfaces[J].Ann.Math.,1969,89(2):187–197.

[18]Li Haizhong,Wei Yong.Classification and rigidity of self-shrinkers in the mean curvature flow[J].J.Math.Soc.Japan,2014,66:709–734.

[19]Liu Huaqiao,Xin Yuanlong.Some results on space-like self-shrinkers[J].Acta Math.Sin.(Engl.Ser.),2016,32(1):69–82.

[20]McGonagle M,Ross J.The hyperplane is the only stable and smooth solution to the isoperimetric problem in Gaussian space[J].Geom.Dedi.,2015,178(1):277–296.

[21]Okumura M.Hypersurfaces and a pinching problem on the second fundamental tensor[J].Amer.J.Math.,1974,96:207–213.

[22]Palmer B.The Gauss map of a spacelike constant mean curvature hypersurface of Minkowski space[J].Comm.Math.Helv.,1990,65:52–57.

[23]Wu Baoqiang.A Bernstein theorem for complete space-like hypersurfaces of constant mean curvature in Minkowski space[J].Proc.Amer.Math.Soc.,2004,132(1):211–215.

[24]Xin Yuanlong.The Gauss map of a space-like constant mean curvature hypersurface of Minkowski space[J].Comm.Math.Helv.,1991,66(1):590–598.