THE EXISTENCE OF MILD SOLUTION FOR IMPULSIVE FRACTIONAL NEUTRAL FUNCTION INTEGRO-DIFFERENTIAL EVOLUTION EQUATION WITH INFINITE DELAY OF ORDER 0＜α＜1

XUE Zheng-qing,SHU Xiao-bao,XU Fei

(1.College of Mathematics and Econometrics,Hunan University,Changsha 410082,China)

(2.Department of Mathematics,Wilfrid Laurier University,Waterloo N2L 3C5,Canada)

1　Introduction

Fractional differential equation,as an excellent tool for describing memory and hereditary properties of various materials and processes in natural sciences and engineering,received a great deal of attention in the literature[1–5].In particular,the existence of solutions to fractional order differential equations attracted researches attention.For example,the existence of solution for fractional semilinear differential or integro differential equations was extensively investigated[6–10].Recently,mixed type integro-differential systems with and without delay conditions were studied[11–13].Ravichandran and Baleanu[13]considered the existence of solution for the following fractional neutral functional integro-differential evolution equations with infinite delay in Banach spaces

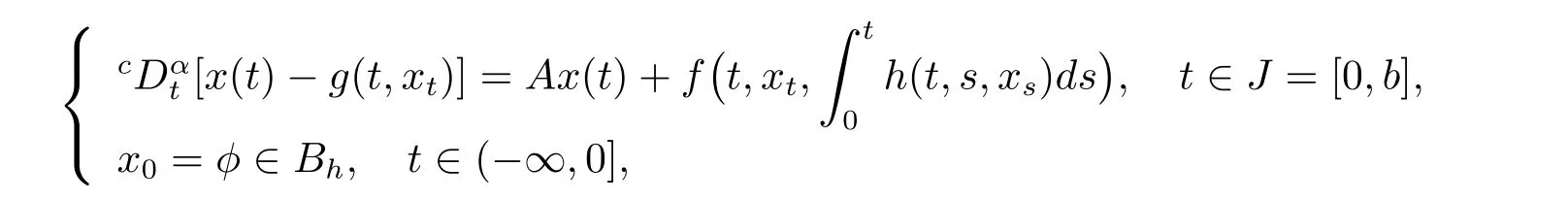
wherecDαtis the Caputo fraction derivative of order 0＜α＜1.By using properties of solution operators and Mönch’s fixed point theorem via measures of noncompactness,the authors developed the existence theorem for such equations.

Motivated by this work,we use Mönch’s fixed point theorem via measure of noncompactness to investigate the existence of mild solution for the following impulsive fractional neutral function integro-differential evolution equations with infinite delay in a Banach space X.

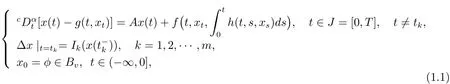
The rest of the paper is organized as follows:in Section 2,some basic definitions,notations and preliminary facts that are used throughout the paper are presented.The definition of mild solution is given in Section 3.The main results are drown in Section 4,in which we present the existence results for impulsive fractional neutral function integro differential evolution equation of order 0＜ α ＜ 1 with infinite delay.

2　Preliminaries

2.1　Definitions and Theorems

Let X be a complex Banach space,whose norm is denoted by ‖·‖.Suppose L(X)is the Banach space of all bounded linear operators from X into X,whose corresponding norm is denoted by ‖·‖L(X).Let C(J,X)denote the space of all continuous functions from J into X,whose supremum norm is given by ‖·‖C(J,X).We use Br(x,X)to denote the closed ball in X with center at x and radius r.

In the paper,we assume that A:D(A)⊂X→X is the infinitesimal generator of a strongly continuous semigroup T(·).Thus there exists a constant M ≤ 1.Without loss of generality,we assume that 0∈ ρ(A).Then we can define the fractional power Aαfor 0＜α≤1,as a closed linear operator on its domain D(Aα)with inverse A−α(see[14]).Aαadmits the following properties.

(1)D(Aα)is a Banach space with norm ‖x‖α= ‖Aαx‖for x ∈ D(Aα).

(2)T(t):X→Xαfor t≥0.

(3)AαT(t)x=T(t)Aαx for each x∈ D(Aα)and t≥ 0.

(4)For every t＞0,AαT(t)is bounded on X and there exists Mα＞0 such that

(5)A−αis a bounded linear operator for 0≤α≤1 in X.

Before introducing a fractional order functional differential equation with infinite delay,we define the abstract phase space Bv.Let v:(∞,0]→ (0,∞)be a continuous function that satisfies

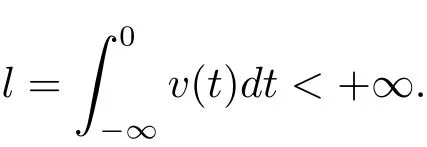
The Banach space(Bv,‖·‖Bv)induced by v is then given by

Bv:={ϕ :(−∞,0)→ X:for any c＞ 0,ϕ(θ)is a bounded and measurable

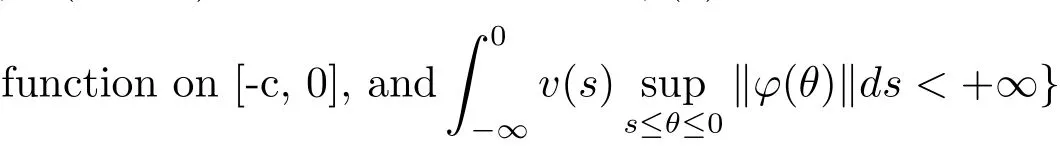
Define the following space

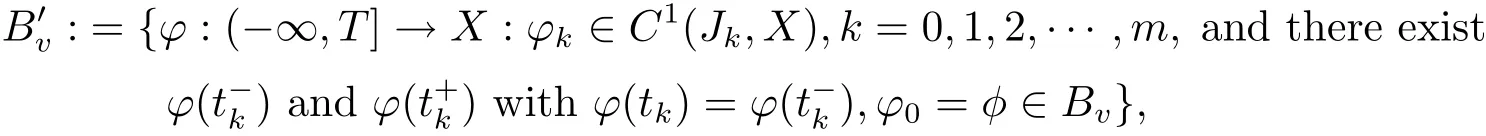
where ϕkis the restriction of ϕ to Jk,J0=[0,t1],Jk=(tk,tk+1],k=1,2,···,m.

where

Generally,the Mittag-Leffler function is defined by

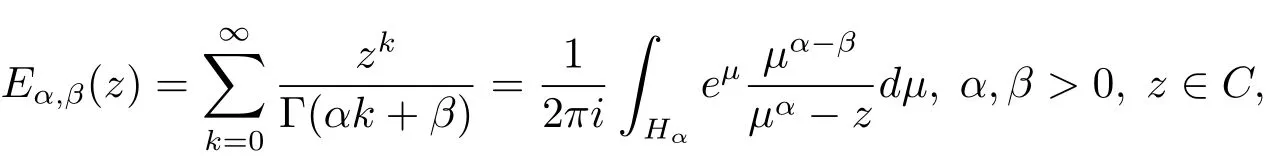
where Hαis a Hankel path,a contour that starts and ends at−∞,and encircles the disccounterclockwise.

Now we consider some definitions about fractional differential equations.

Definition 2.1The fractional integral of order α with the the lower limit zero of a function f is defined as

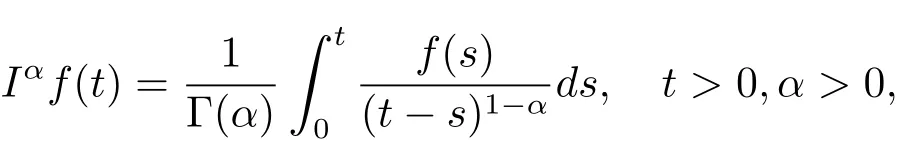
provided that the right-hand side is pointwise defined on[0,∞),where Γ(·)is a gamma

function defined by

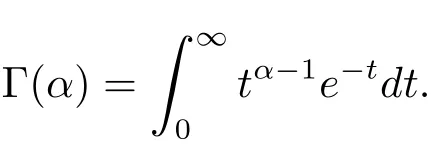
Definition 2.2The Riemann-Liouville fractional derivative of order α ＞ 0,n−1 ＜α＜n,n∈N,is defined as

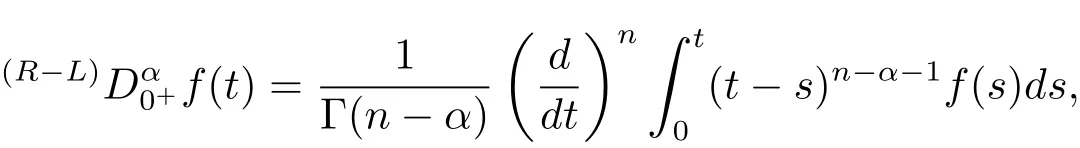
where the function f(t)has absolutely continuous derivative up to order(n−1).

Definition 2.3The Caputo derivative of order α for a function f:[0,∞)→ R can be written as

Lemma 2.1(see[15])Assume x∈,then for t∈J,xt∈Bv.Moreover,

where

Next,we consider some definitions and properties of the measures of noncompactness.

The Hausdorff measure of noncompactness β(·)defined on each bounded subset B of Banach space X is given by Some basic properties of β(·)are given in the following lemma.

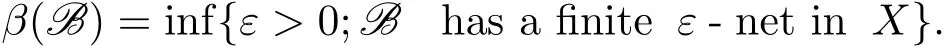
Lemma 2.2(see[16–18])If X is a real Banach space andB,D ⊂ X are bounded,then the following properties are satisfied:

(1)monotone:if for all bounded subsets B,D of X,B ⊆ Dimplies β(B)≤ β(D);

(2)nonsingular:β({x}∪B)= β(B)for every x∈ X and every nonempty subset B⊂X;

(3)regular:Bis precompact if and only if β(B)=0;

(4)β(B+D)≤β(B)+β(D),where B+D={x+y;x∈B,y∈D};

(5) β(B∪D)≤ max{β(B),β(D)};

(6) β(λB)≤ |λ|β(B);

(7)if W ⊂C(J,X)is bounded and equicontinuous,then t→β(W(t))is continuous on J,and

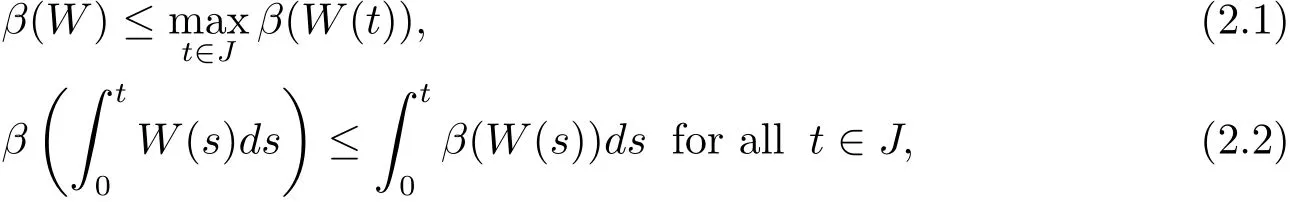
where

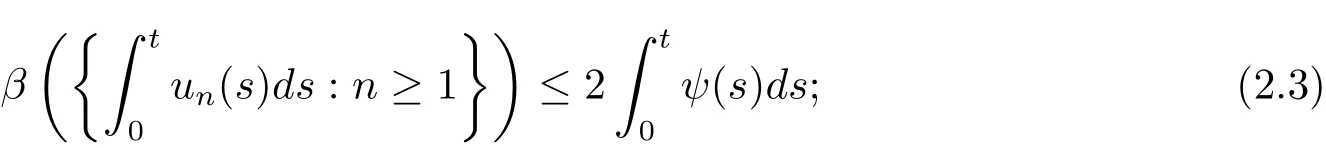
(9)if W is bounded,then for each ε ＞ 0,there is a sequencesuch that

The following lemmas about the Hausdorffmeasure of noncompactness will be used in proving our main results.

Lemma 2.3(see[19])Let D be a closed convex subset of a Banach space X and 0∈D.Assume that F:D → X is a continuous map which satisfies the Mönch’s condition,that is,M⊆D is countable,is compact.Then F has a fixed point in D.

2.2　Properties of Solution Operators

Lemma 2.4(see[20])If A is a sectorial operator of type(M,θ,α,µ),then

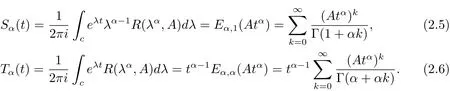
Lemma 2.5(see[13])Assuming A is the infinitesimal generator of an analytic semigroup,given by T(t)t≥0and 0 ∈ ρ(A),then we now have

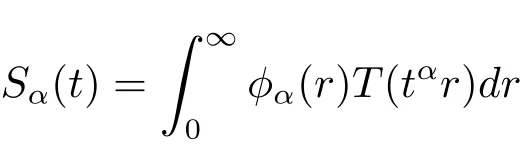
and

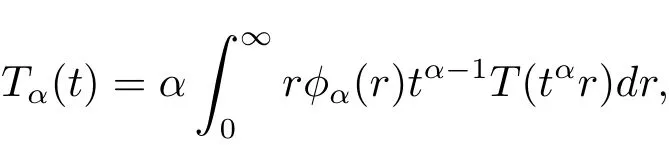
where

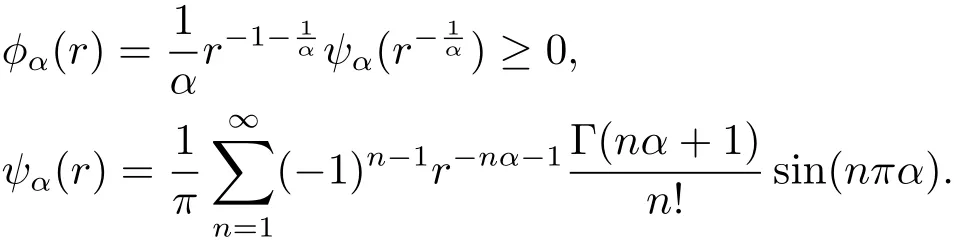
Lemma 2.6(see[21])

where α,β ∈ (0,1).

Lemma 2.7Suppose A is a sectorial operator of type(M,θ,α,µ).If 0 ＜ α ＜ 1,then

and

3　Definition of Mild Solution

Theorem 3.1If f satisfies a uniform Hölder condition with exponent β ∈ (0,1]and A is a sectorial operator of type(M,θ,α,µ),then the Cauchy problem(1.1)has a solution,given by

ProofFor all t∈ (tk,tk+1]where k=0,1,···,m by Lemma 2.7,we obtain

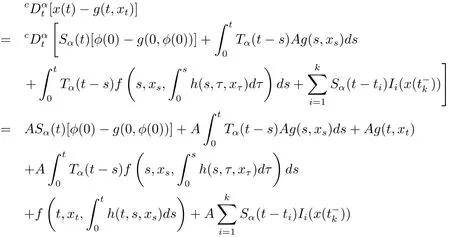
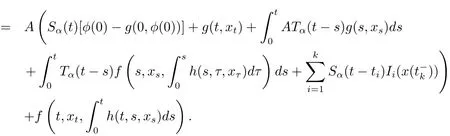
Thus expression(3.1)satisfies the first equation of problem(1.1).

For k=1,2,···,m,it follows from(3.1)that

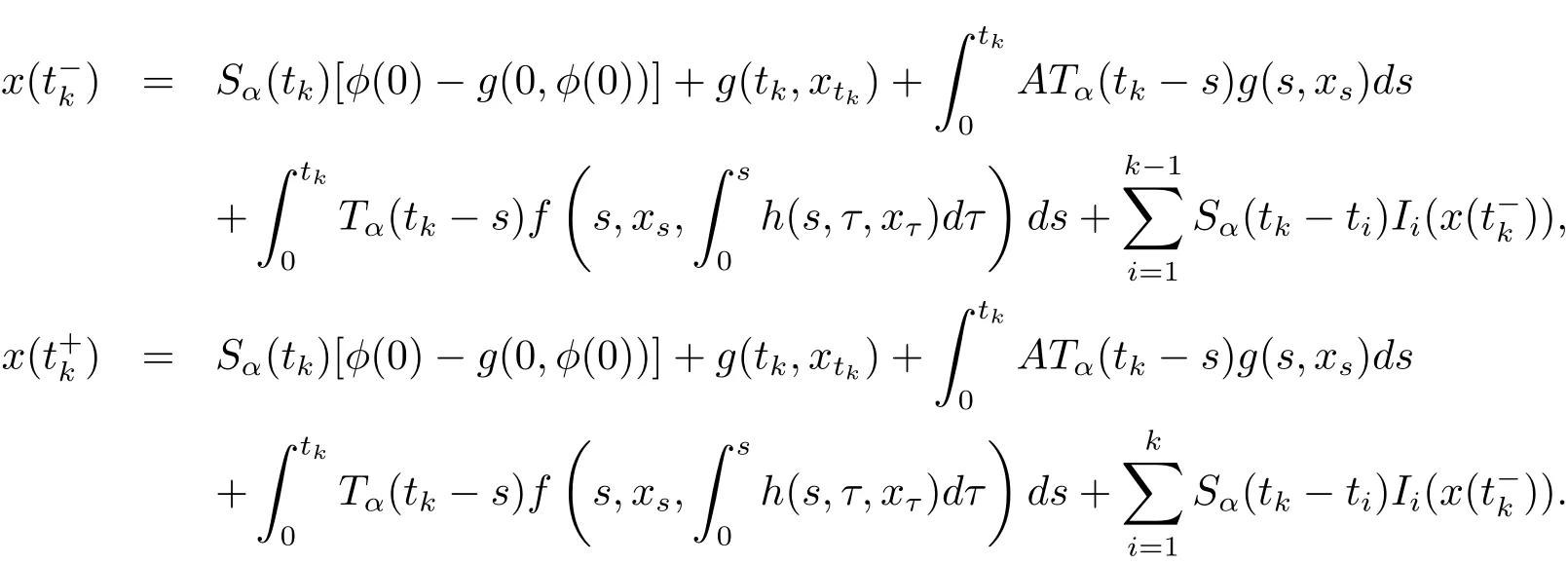
Therefore we have

Consequently,all the conditions of problem(1.1)are satisfied.Hence(3.1)is a solution of problem(1.1).

Thus the mild solution of equation(1.1)can be defined as follows.

Definition 3.1(see[22])A continuous function x:(−∞,T]→ X is said to be mild solution of system(1.1)if x= φ ∈ Bvon(−∞,0],the impulsive condition∆x(tk)=Ik(x()),k=1,2,···,m is satisfied,the restriction of x(·)to the interval Jkis continuous,and x(t)satisfies the following integral equation

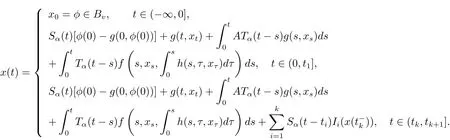
4　Existence Results

In this section,we present the main results of this article.We first consider the following hypotheses.

If A is a sectorial operator of type(M,θ,α,µ),then ‖Sα(t)‖ ≤ Meωtand ‖Tα(t)‖ ≤Ceωt(1+tα−1).Let

where L(X)is the Banach space of bounded linear operator from X into X equipped with its natural topology.Thus we have

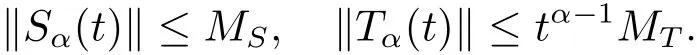
We assume the following conditions hold

(H1)The function f:J×Bv×X→X satisfies the following conditions:

(i)f(·,φ,x)is measurable for all(φ,x) ∈ Bv× X and f(t,·,·)is continuous for a.e.t∈J.

(ii)There exist a constant α1∈ (0,α),and a positive integrable function Ω:R+→R+such that

for all(t,φ,x)∈ J × Bv× X,where Ω satisfies

(iii)There exist a constant α2∈ (0,α)and a functionsuch that,for any bounded subset D1⊂X,F1⊂Bv,

for a.e.t∈ J,where F1(θ)={v(θ):v ∈ F1}and β is the Hausdorff MNC.

(H2)The function h:J×J×Bv→X satisfies the following conditions:

(i)h(·,t,x)is measurable for all(t,x) ∈ J ×Bvand h(t,·,·)is continuous for a.e.t∈ J.

(ii)There exist a constant H0＞0 such that

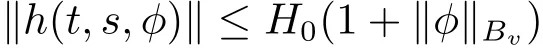
for all t,s∈J,φ∈Bv.

(iii)There exists ξ∈ L1(J2,R+)such that for any bounded subset F2⊂ Bv,

(H3)The function g:J×Bv→X satisfies the following conditions:

(i)g is continuous and there exist a constant H1＞0 and 0＜β＜1 such that g is Xβvalued and

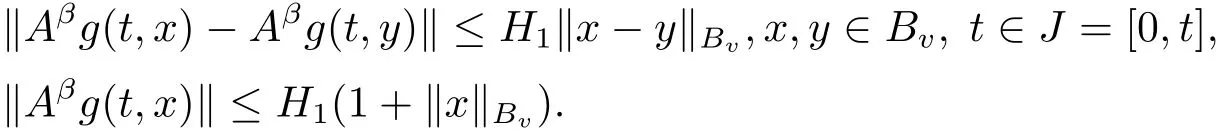
(ii)There exist a constant α3∈ (0,α)and g∗such that,for any bounded subset F3⊂Bv,

(H4)Ii:X→X be continuous operators and there exist positive numbers ci,Kisuch that

for every bounded subset F4of

(H5)

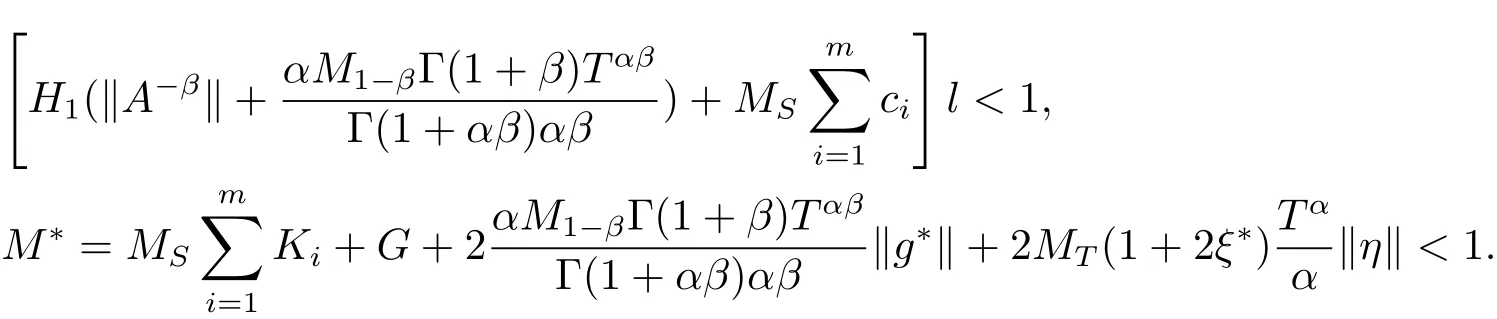
Theorem 4.1Suppose conditions(H1)–(H5)are satisfied.Then system(1.1)has at least one solution on J.

ProofWe define the operator Γ

The operator Γ has a fixed point if and only if system(1.1)has a solution.For φ ∈ Bv,denote

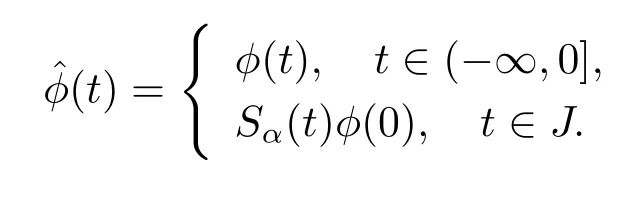
if and only if x(t)satisfies x(t)= φ(t),t∈ (−∞,0]and

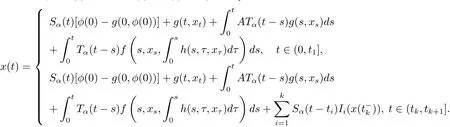
It is easy to see that operator Γ has a fixed point if and only if operator N has a fixed point.In the following,we prove that N has a fixed point.

Step 1We prove that there exists some r＞0 such that N(Br)⊂Br.If this is not true,then,for each positive integer r,there exist yr∈ Brand tr∈ (−∞,T]such that‖(Nyr)(tr)‖ ＞ r.

On the other hand,it follows from the assumption that

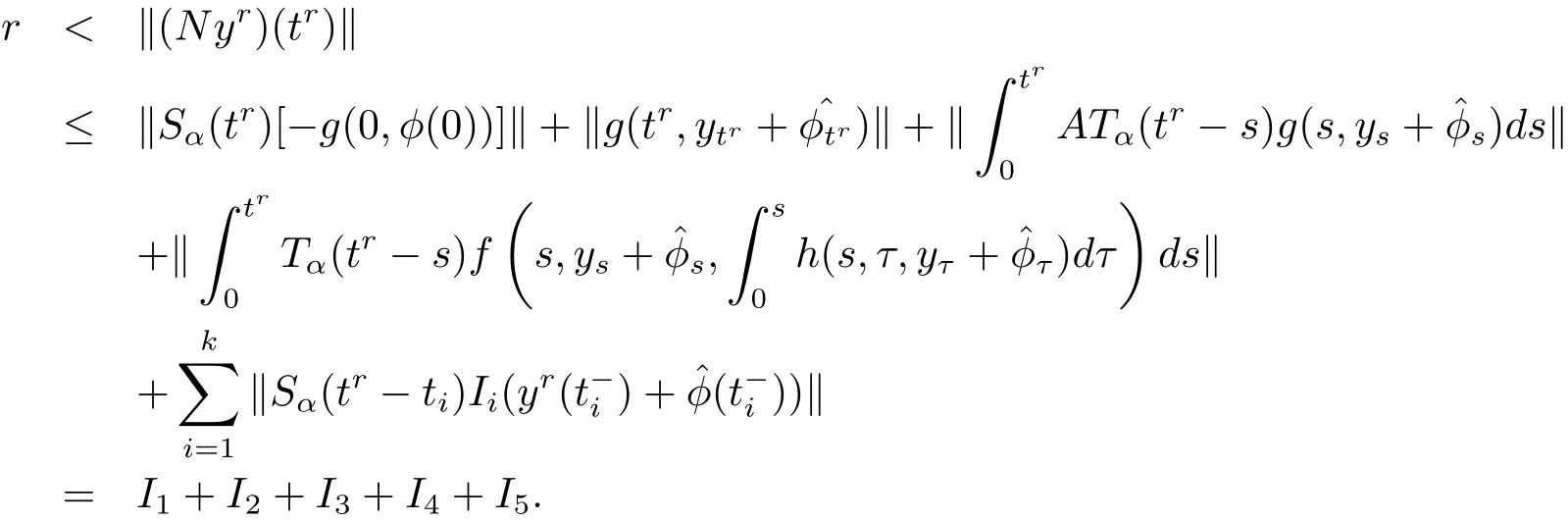
Now we estimate Ii,i=1,2,3,4,5.Assumption(H3)(i)implies

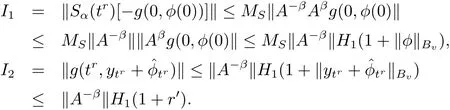
It follows from assumption(H3)(i)and Hölder’s inequality that

By using assumptions(H1)and(H2),we obtain

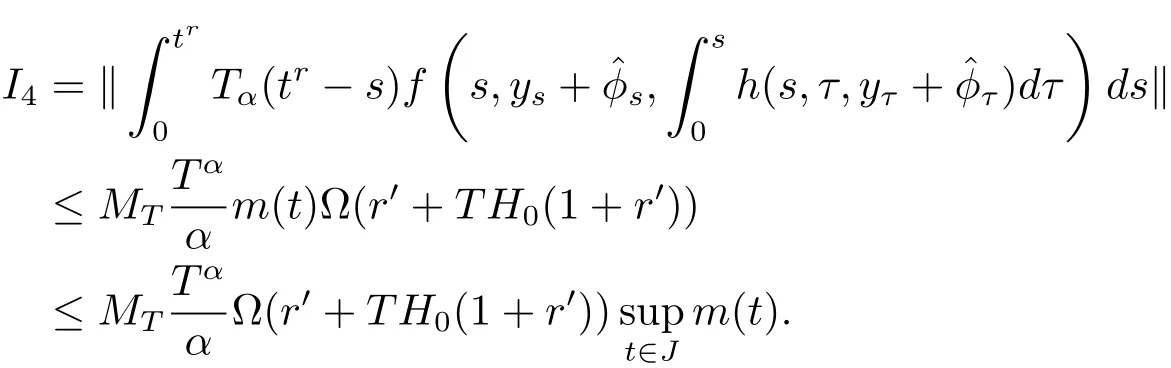
Using assumptions(H1)(i)and(H4)yields

Combining estimates I1−I5,we obtain

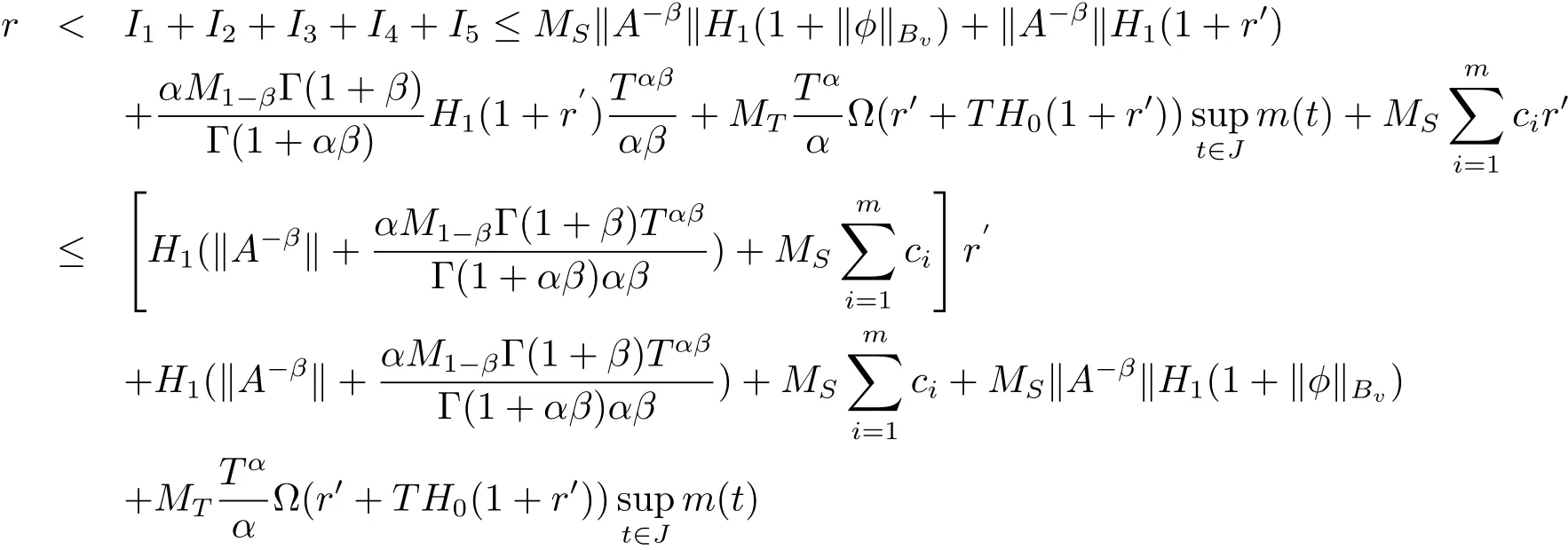
Dividing both sides by r and taking r→+∞ from

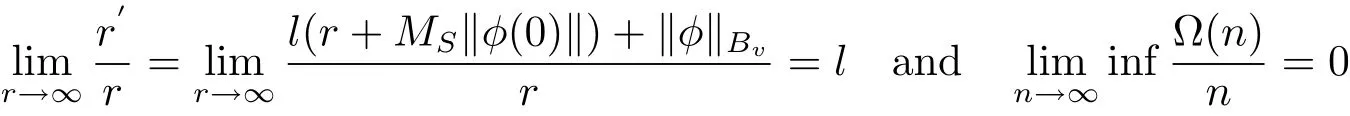
yields

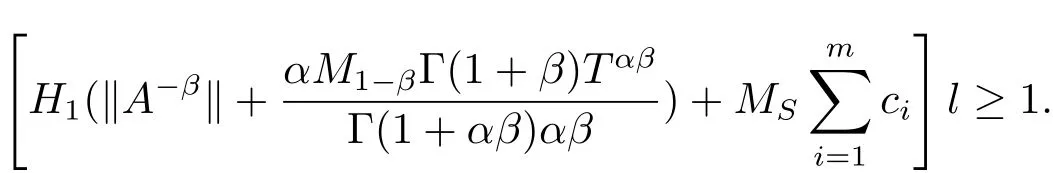
This contradicts(H5).Thus,for some number r,N(Br)⊂Br.

Step 2N is continuous on Br.

Now for every t∈[0,t1],we have

Moreover,for all t∈ (tk,tk+1],k=1,2,···,m,we have

We thus obtain‖Nyn−Ny‖→0 as n→∞implying that N is continuous on Br.

Step 3The map N(Br)is equicontinuous on J.

The function{Ny:y∈Br}is equicontinuous at t=0.For 0＜t1＜t2≤T,t1,t2∈(tk,tk+1],k=1,2,···,m and y ∈ Br,by assumptions(H1)and(H4),we deduce that

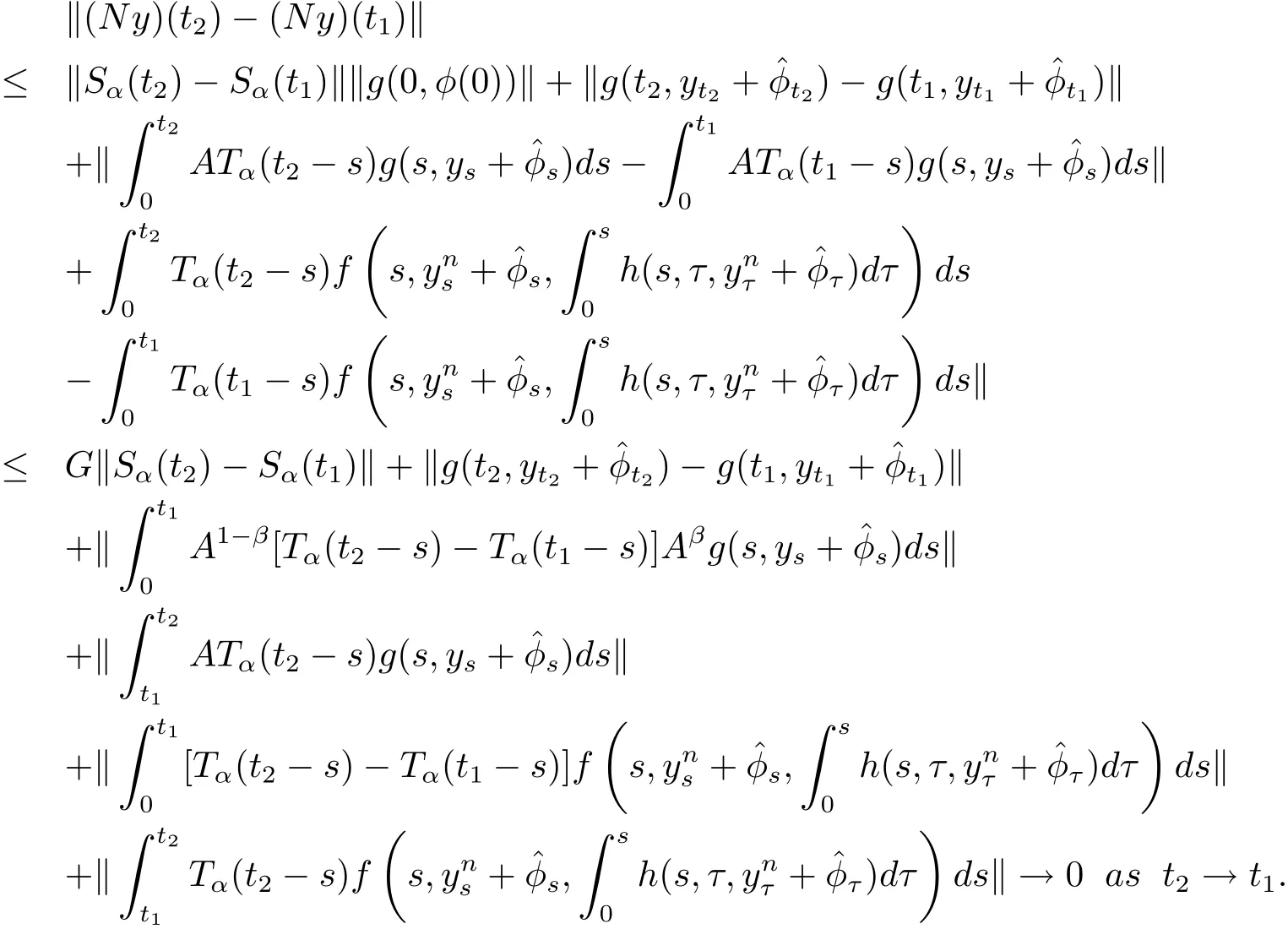
Hence N(Br)is equicontinuous on J.

Step 4Mönch’s condition holds.

Let N=N1+N2+N3,where

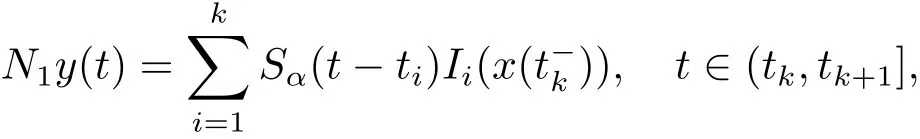
Assume W⊆Bris countable and W⊆({0} ∪ N(W)).We show that β(W)=0,where β is the Hausdorff MNC.Without loss of generality,we may suppose that W=Since N(W)is equicontinuous on Jk,W ⊆({0}∪N(W))is equicontinuous on Jkas well.

By(H4)(ii),we have

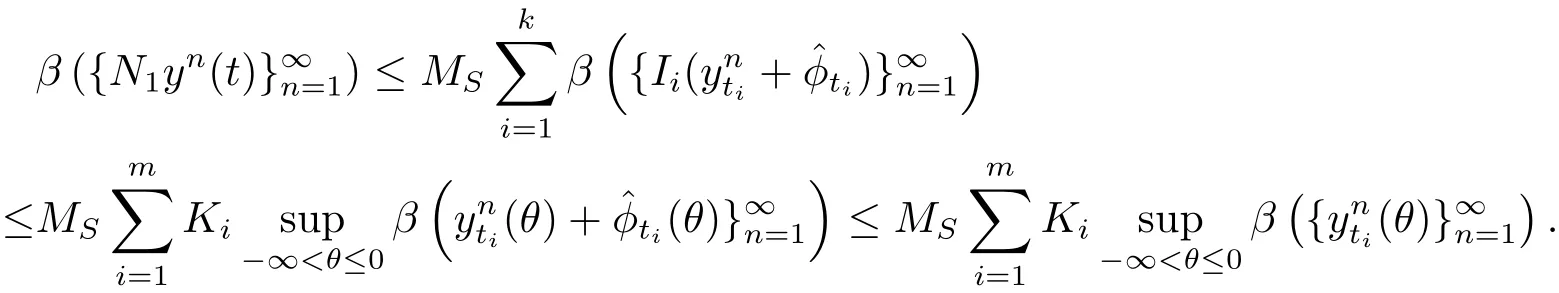
Using Lemma 2.2,(H1)(iii),(H2)(iii)and(H3)(ii),we have

We thus obtain

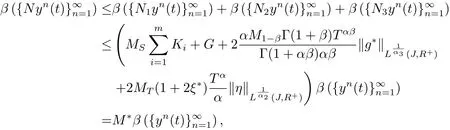
where M∗is defined in assumption(H5).Since W and N(W)are equicountinuous on every Jk,it follows from Lemma 2.2 that the inequality implies β(NW) ≤ M∗β(W).Thus from Mönch’s condition,we have

Since M∗＜ 1,we get β(W)=0.It follows that W is relatively compact.Using Lemma 2.3,we know that N has a fixed point y in W.The proof is completed.

[1]Kilbas A A,Srivastava H M,Trujillo J J.Theory and applications of fractional differential equations[M].New York:North-Holland,2006.

[2]Podlubny I.Fractional differential equations[M].San Diego:Academic Press,1990.

[3]Liu Zhenhai,Sun Jihua.Nonlinear boundary value problem of fractional differential systems[J].Comput.Appl.Math.,2012,64(4):463–475.

[4]Miller K S,Ross B.An introduction to the fractional calculus and differential equations[M].New York:John Wiley,1993.

[5]Zhou Yong,Jiao Feng.Nonlocalcauchy problem for fractional evolution equations[J].Nonl.Anal.,2010,11(5):4465–4475.

[6]Zhou Yong,Jiao Feng.Existence of mild solution for fractional neutral evolution equations[J].Comput.Math,Appl.,2012,59(3):1063–1077.

[7]Baleanu D,Mustafa OG.On the global existence of solutions to a class of fractional differetial equations[J].Comput.Math.Appl.,2012,59(5):1835–1841.

[8]Baleanu D,Mustafa OG,Agarwal RP.An existence result for a superlinear fractional differential equation[J].Appl.Math.Lett.,2010,23(9):1129–1132.

[9]dosSantos JPC,Arjunan MM,Cuevas C.Existence results for fractional neutral integro-differential equations with state dependent delay[J].Comput.Math.Appl.,2011,62(3):1275–1283.

[10]dos Santos JPC,Vijayakumar V,Murugesu R.Existence of mild solutions for nonlocal Cauchy problem for fractional neutral integro-dofferential equation with unbounded delay[J].Commun.Math.Anal.,2013,14(1):59–71.

[11]Dhakne MB,Kucche KD.Existence of a mild solution of mixed Volterra-Fredholm functional integro-differential equation with nonlocal condition[J].Appl.Math.Sci.,2011,5(8):359–366.

[12]Ntouyas SK,Purnaras IK.Existence results for mixed Volterra-Fredholm type neutral functional integro-differential equations in Banach spaces[J].Nonl.Stud.,2009,16(2):135–148.

[13]Ravichandran C,Baleanu D.Existence results for fractional neutral functional integro-differential evolution equations with infinite delay in Banach spaces[J].Adv.Diff.Equ.,2013,215:1–12.

[14]Pazy A.Semigroups of linear operators and applications to partial differential equations[M].New York:Springer,1983.

[15]Yan Baoqiang.Boundary value problems on the half-line with impulses and infinite delay[J].J.Math.Anal.Appl.,2001,259(1):94–114.

[16]Ji Shaochun,Li Gang,Wang Min.Controllability of impulsive differential systems with nonlocal conditions[J].Appl.Math.Comput.,2011,217(16):6981–6989.

[17]Lakshmikantham V,Leela S.Nonlinear differential equations in abstract spaces[M].New York:Pergamon Press,1969.

[18]Monch H.Boundary value problems for nonlinear ordinary differential equations of second order in Banach space[J].Nonl.Anal.,1980,4:985–999.

[19]Bellman R.The stability of solutions of linear differential equations[J].Duke Math.J.,1943,10(4):643–647.

[20]Shu Xiaobao,Xu Fei.Upper and lower solution method for fractional evolution equations with order 1＜α ＜ 2[J].J.Korean Math.Soc.,2014,51(6):1123–1139.

[21]Shu Xiaobao,Xu Fei,ShiYajing:S-asymptotically ω-positive periodic solutions for a class of neutral fractional differential equations[J].Appl.Math.Comput.,2015,270:768–776.

[22]Shu Xiaobao,Wang Qianqian.The existence and uniqueness of mild solutions for fractional differential equations with nonlocal conditions of order 1＜α＜2[J].Comput.Math.Appl.,2012,64(6):2100–2110.

[23]Shu Xiaobao,Lai Yongzeng,Chen Yuming.The existence of mild solutions for impulsive fractional partial differential equations[J].Nonl.Anal.,2011,74(5):2003–2011.

[24]Shu Xiaobao,Shi Yajing.A study on the mild solution of impulsive fractional evolution equations,Applied Mathematics and Computation,2016,273:465–476.

[25]Shi Yajing,Shu Xiaobao.The existence of mild solutions for impulsive fractional differential equations with nonlocal conditions of order 1＜α ＜ 2[J].J.Math.,2017,37(3):647–658.