A SCHUR’S LEMMA FOR BAKRY-EMERY RICCI CURVATURE ON KÄHLER MANIFOLDS

HUANG Guang-yue

(Department of Mathematics,Henan Normal University,Xinxiang 453007,China)

1　Introduction

The Ricci soliton is a natural generalization of Einstein metrics,which is a self-similar solution to Hamiltion’s Ricci flow.In[1],Pigola,Rigoli,Rimoldi and Setti introduced the gradient Ricci almost soliton.That is,if there exist two smooth functions f,λ such that

then(Mn,g)is called a gradient Ricci almost soliton,where Rij+fijis called the∞-dimensional Bakry-Emery Ricci tensor.Clearly,a gradient Ricci soliton is a special case of the gradient Ricci almost soliton when λ is a constant.In particular,if λ = ρR+ µ,where R is the scalar curvature and ρ,µ are two constants,then(1.1)is called the gradient ρ-Einstein soliton defined in[2]which is a self-similar solution to the following geometric flow first considered by Bourguignon in[3]

For some study with respect to the gradient Ricci almost soliton,the interested reader can refer to[1,4–7]for more details.

Note that if f given in(1.1)satisfies fij=0,then(1.1)becomes

and the classical Schur’s lemma states that the scalar curvature R=nλ must be a constant when n≥3.However,there exist gradient Ricci almost solitons with nontrivial function f such that λ is not a constant.A natural question is to consider whether can one find manifolds satisfying(1.1)with nontrivial function f on which λ is constant.In this paper,we consider this problem on Kähler manifolds and prove the following results.

Theorem 1.1Let(Mn,g)be an n-dimensional Kähler manifold with n ≥ 2.If there exist two smooth real-valued functions f,λ satisfying the equation

then λ must be a constant.

Therefore,by virtue of Theorem 1.4 of Chen and Zhu in[8],we obtain the following.

Corollary 1.2Let(Mn,g)be an n-dimensional(n ≥ 2)complete Kähler manifold with harmonic Bochner tensor.If there exist two smooth real-valued functions f,λ satisfying(1.4)with fij=0(that is,▽f is a holomorphic vector field),then we have

1)if the function λ ＞ 0,then(Mn,g)is isometric to the quotient of Nk×Cn−k,where Nkis a k-dimensional Kähler-Einstein manifold with positive scalar curvature;

2)if the function λ ＜ 0,then(Mn,g)is isometric to the quotient of Nk×Cn−k,where Nkis a k-dimensional Kähler-Einstein manifold with negative scalar curvature.

RemarkIf λ defined in(1.4)is a constant,then it is called a Kähler-Ricci soliton.For the classification of the Kähler-Ricci soliton,we refer to[8,9].

2　Proof of Results

Using the concepts as in[8],under the Kähler metric g=(g),the Ricci curvature and the scalar curvature defined by

respectively.By the first Bianchi identity,we have

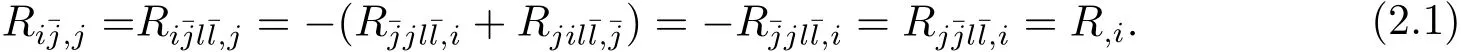
By virtue of(1.4),we obtain

Therefore,from(2.3),we obtain

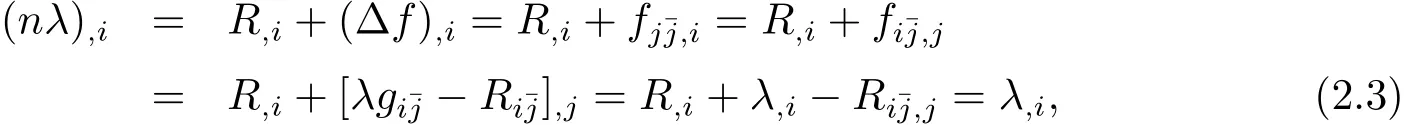
where in the third equality we used

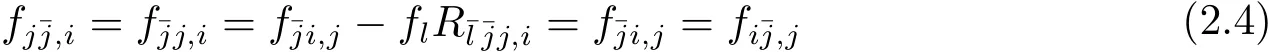
and in the last equality we used(2.1).Therefore,from(2.4),it is easy to see that

which shows that λ is a constant.

We complete the proof of Theorem 1.1.

[1]Pigola S,Rigoli M,Rimoldi M,Setti A.Ricci almost solitons[J].Ann.Sc.Norm.Super.Pisa Cl.Sci.,2011,10(4):757–799.

[2]Catino G,Mazzieri L.Gradient Einstein solitons[J].Nonl.Anal.,2016,132:66–94.

[3]Bourguignon J P.Ricci curvature and Einstein metrics[M].Notes Math.,Vol.838,Berlin:Springer,1981,42–63.

[4]Barros A,Ribeiro JR E.Some characterizations for compact almost Ricci solitons[J].Proc.Amer.Math.Soc.,2012,140(3):1033–1040.

[5]Barros A,Ribeiro JR E.Characterizations and integral formulae for generalized m-quasi-Einstein metrics[J].Bull.Braz.Math.Soc.(N.S.),2014,45(2):325–341.

[6]Huang G Y,Wei Y.The classification of(m,ρ)-quasi-Einstein manifolds[J].Ann.Glob.Anal.Geom.,2013,44(3):269–282.

[7]Zeng F,Ma B.The classification of gradient Ricci almost solitons[J].J.Math.,2014,34(2):251–258.

[8]Chen Q,Zhu M.On rigidity of gradient Kähler-Ricci solitons with harmonic Bochner tensor[J].Proc.Amer.Math.Soc.,2012,140(11):4017–4025.

[9]Su Y,Zhang K.On the Kähler-Ricci solitons with vanishing Bochner-Weyl tensor[J].Acta Math.Sci.Ser.B Engl.Ed.,2012,32(3):1239–1244.