基于H-P滤波与VMD的行星齿轮箱故障诊断

李耀祖，王细洋

(南昌航空大学 航空制造工程学院，南昌 330063)

0　引言

在传统的机械设备、机械装置以及传动系统中，齿轮箱是必不可少的零部件，它能承受高强度、高负荷等恶劣的工作环境，而在现今工作环境中行星齿轮箱应用较为广泛。行星齿轮箱具有许多优点，如重量轻、传动比大、体积小、传动效率高与承载能力强等[1]，因此对行星齿轮箱的早期预防与故障诊断显得尤为重要，齿轮断裂、点蚀、裂痕等是常见的故障，在行星齿轮箱诊断方法中，使用振动信号对其研究比较普遍，其不足之处就是振动信号容易受其他振动源以及齿轮相对位置等影响[2]，使得振动信号的幅值、频率出现调制现象[3]，不利于对故障特征的提取与分析，与振动信号相比，扭振信号基本不受其影响，扭振信号的信噪比较高、传递路径简单，是现在故障诊断领域常用的一种信号。

H-P滤波方法是将信号分解成噪声信号和趋势信号，滤波后去除噪声部分，保留其趋势信号。H-P滤波最早是应用于经济领域，用于分析一些经济的显著特征，该方法与传统的小波方法有所不同。运用小波方法需选取相应的基函数与原始信号进行卷积[4-5]，且最终的诊断效果与选取的基函数密切相关，而H-P滤波不需要选取基函数，操作更为简单；因此，本研究尝试将H-P滤波应用于故障诊断领域。然而，经过H-P滤波保留下来的趋势信号是一个多内容的复合信号，研究所需的故障信号包含在其中，需要进一步对其分解。VMD属于自适应分解信号的方法，能有效地将信号分解成不同模态下的特定信号，分解后可得到单独的故障信号，故障特征明显，能很好地诊断出相应故障。VMD也是一种较为新型的信号分解方法[6]。

针对以上叙述，本研究将H-P滤波与VMD方法相结合应用于行星齿轮箱的故障诊断中。先用H-P滤波对采集的原信号进行滤波，去除噪声信号保留实际所需的趋势信号，再将其用VMD进行分解，分离出特定的故障信号，提取行星齿轮箱相关的故障特征。

1　H-P滤波与VMD原理

1.1　H-P滤波原理

H-P滤波是Hodrick Prescott在1997年提出，应用于经济领域的一种规则化滤波方法[7]。它是一种基于时间序列在状态空间上的分析方法，使其波动方差达到极小化，之后，有大量学者对其进行改进后研究，并应用于其他领域。比如在差分自回归滑动模型当中，需要对趋势项计算以及对该项的平稳度进行处理，这时就可以采用H-P滤波方法分解出趋势项和它的周期[8]，达到较好的效果。H-P滤波也可以看作为一个基于时间序列频谱的高通滤波器，保留高频部分，去除低频部分。在实际操作中H-P滤波就是求解一个最优问题的过程，整个目标函数可分为2项：一项是与趋势项光滑程度相关的函数，另一项是与残差项相关的函数，目标函数通过调整参数将两项相连，式(1)、式(2)是相应的数学表达式[9]。

(1)

其中

(2)

其中：x为内在趋势序列，x∈Rn；y为实际序列，y∈Rn；λ为调整参数；Dx为二次差分项；u为公式通项；δ为大于0的实数，δ∈Rn。

1.2　VMD原理

变分模态分解(VMD)是在2014年由Dragomiretskiy等所提出来的，主要是靠循环迭代约束最优解从而得到关于模态分量的中心频率、频带宽，最终使得各个频率实现有效分离[10]。VMD通过分解信号并形成非递归、变分模态分解模式，非递归分解的信号显著特点是收敛较快[11]，例如，白堂博等[12]将VMD方法应用到旋转机械故障诊断的研究，将信号经过VMD，然后从对故障特征分量进行包络谱与时频域分析。以下是VMD的具体求解过程。

首先将输入信号依次分解为若干个具有特定稀疏特性的子信号，这是VMD原理的实质，现给定扭振信号V，VMD方法在求解约束变分问题时可将信号V分解成不同的模态分量，每个模态分量的带宽都是有限的，式(3)为约束变分问题的数学表达式[10]。

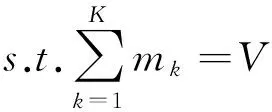
(3)

式中：K为信号分解后的模态总数，wk、mk分别为对应分解后第k个模态的中心频率和时域信号。在对式(3)求解时，需要引用Lagrange乘以二次惩罚项，二次惩罚项主要作用是降低高斯噪声的干扰，使用Lagrange乘子目的是加强约束的严格性，式(4)为增广变分问题数学表达[10]。

L(mk,wk,β)=

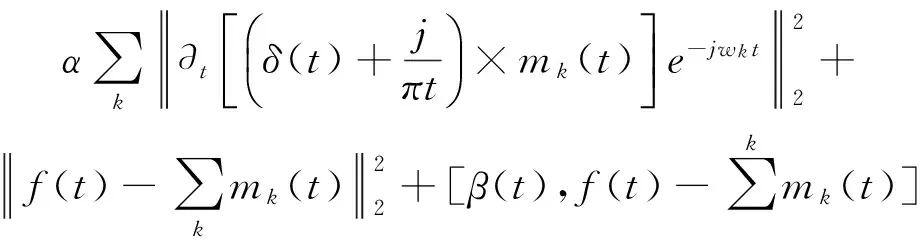
(4)

在求解式(4)的变分问题时，运用对偶分解和Lagrange法的交替方向乘子方法(Alternate Direction Method of Multipliers，ADMM)，然后对mk、wk与β依次进行交替迭代寻优，得到式(5)～式(7)迭代公式。

(7)

给定求解精度ε，当满足式(8)时停止迭代。

(8)

VMD迭代求解的具体过程如下：

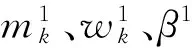
2)由迭代公式(5)、式(6)更新mk、wk。

3)通过式(7)更新β，n=n+1。

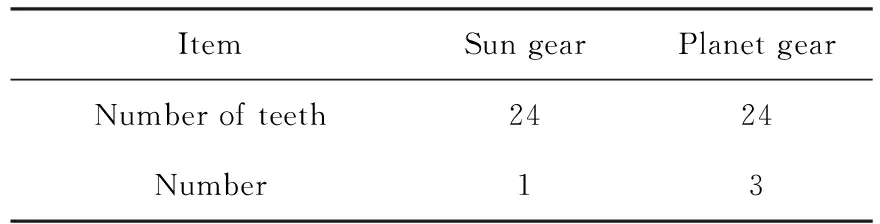
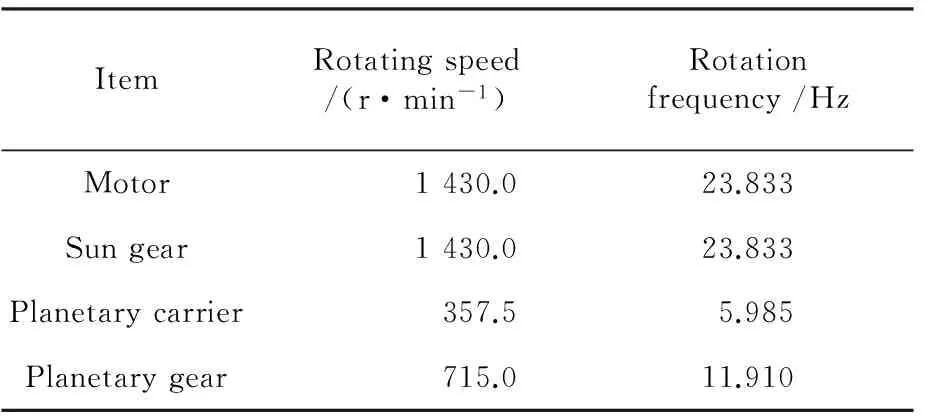
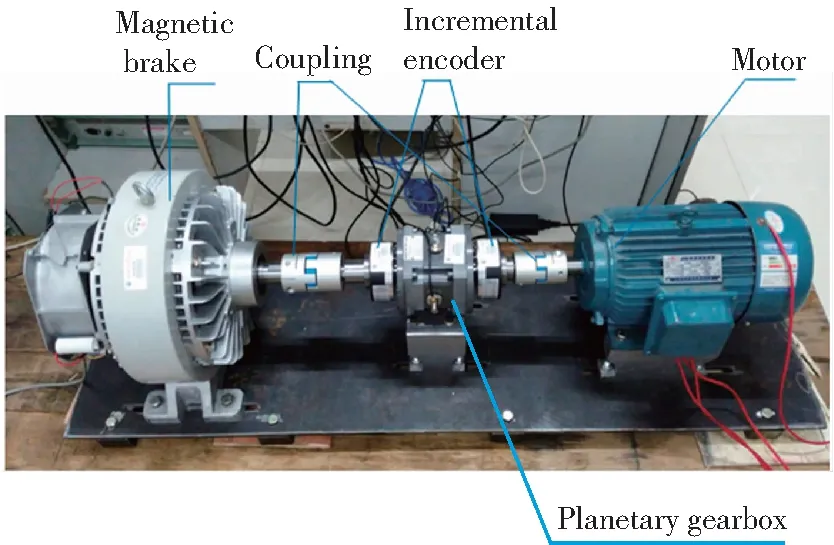
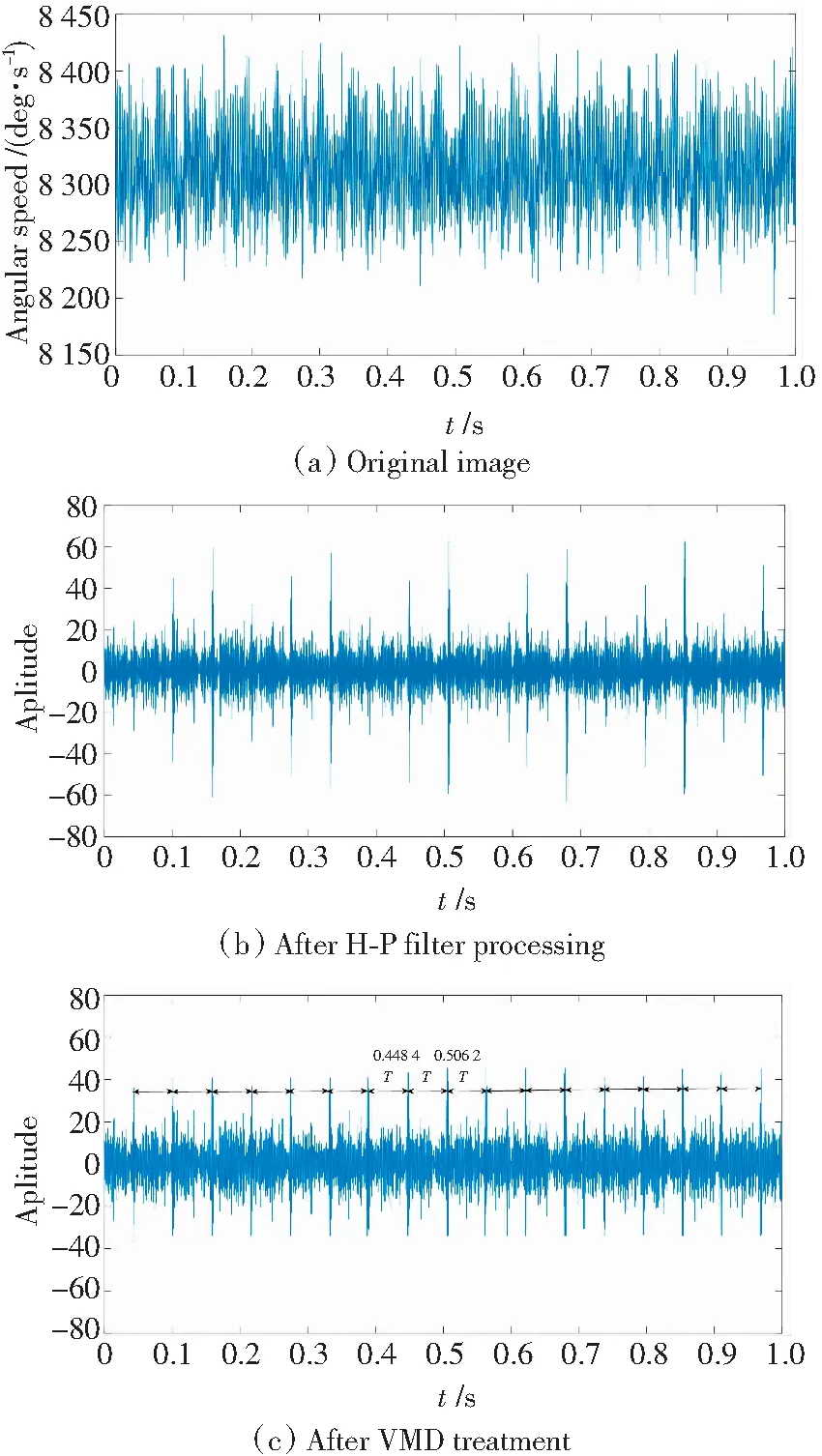
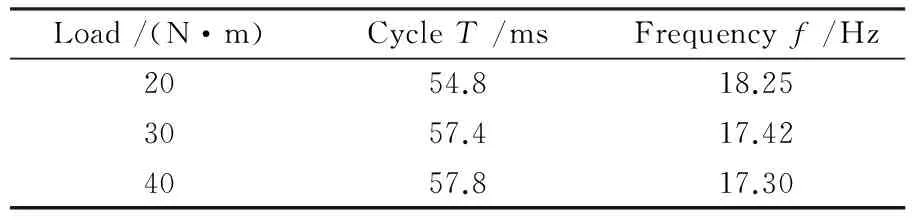
4)根据表达式(8)判断收敛性：如果不收敛且n

最后对K值的影响进行分析，由试验研究表明，模态总数K对VMD的分解性能影响较大，当对振动信号降噪分析时，如果K值偏大，在不同的模态分量中可能会出现振动信号的某一频带成分，在降噪过程中有利于保留原始振动信号中的特征频率成分；反之，如果K值偏小，则邻近的模态上将出现部分模态，特别是在强高斯噪声环境下容易出现噪声信号与特征频带信号的混叠，使得信号去噪难度加大。对扭振信号分解去噪时尽可能使K值取大。

2　试验设备

试验中齿轮箱属于单级传动齿轮箱，其型号为PXDS115-4。表1为行星齿轮箱的设备参数，电机转速为1 430 r/min。表2为行星齿轮箱相关运行参数，啮合频率为429 Hz，转频=转速/60。

表1　行星齿轮箱设备参数Table 1　Planetary gear box equipment parameters

表2　行星齿轮箱相关运行参数Table 2　Related operation parameters of planetary gear box

图1所示为试验台系统，主要由电动机、增量式编码器、联轴器、磁粉制动器、行星齿轮箱5部分组成，磁粉制动器起到增加负载的作用。

3　故障齿轮扭振信号分析

行星齿轮箱经常在重载荷、高转速等恶劣环境下运行，容易导致齿轮的局部损伤甚至齿轮断裂等严重现象，之前在行星齿轮诊断领域，大多数是应用横向振动信号进行信号分析，但是针对行星齿轮箱中不同齿轮间特殊的组合结构，横向振动信号在诊断时具有一定的局限性，容易产生调幅调频现象，其原因前面已有叙述，因此，为了更好地分析齿轮故障，尽可能减少外在因素对试验的影响，扭振信号作为本研究的首选诊断信号。在整个试验过程中人为设置齿轮故障，将其中1个行星齿轮进行破坏(图2)，根据式(9)[13]可得太阳轮与行星轮的局部故障频率分别为fs=53.63 Hz，fp=17.875 Hz。

图1　试验平台Fig.1　Experiment platform

(9)

其中：Zs为太阳轮齿数；N为行星轮数量；Zp为行星轮齿数；fm为啮合频率。

图2　行星轮断齿位置Fig.2　Position of broken teeth of the planetary gear

通过试验台对数据进行采集，采集的信号由增量式编码器与采集卡相结合，通过相应的方法对角域信号进行重构，最终转换成角速度形式的扭振信号。为了使试验更接近于实际工况，以及更具有实际意义，防止行星齿轮发生空转，试验时使用磁粉制动器对试验系统施加相关的负载，本试验分别对扭矩为20、30、40 N·m时扭振信号进行采集，分析在不同负载条件下，经H-P滤波与VMD处理后的时域图形，并将其处理前后的时域图进行对比。

图3～图5依次是负载为20、30、40 N·m时经2种方法处理前后的3组时域图形对比，分别包括未处理的原始图、H-P处理后的图、VMD处理后的图。由图可以看出：对采集的信号先使用H-P滤波然后再进行VMD处理的时域效果比较明显，发现最终处理后的信号均出现周期为T的信号脉冲，相对于其他成分所产生的脉冲更为明显。以图3为例，其脉冲周期T=0.410 1-0.355 3=0.054 8 s(即54.8 ms)，f=1/T=18.25 Hz，经计算的f与行星轮故障频率fp相接近，误差产生主要是因为增加了负载，实际转速有所变化，属于正常误差范围之内，可以看做f=fp，说明行星轮出现了故障，该方法能有效地提取行星齿轮故障特征。为了进一步验证本研究所提出方法的有效性，通过磁粉制动器调节负载，观察采集的原始扭振信号在不同负载下经过H-P滤波与VMD处理后的效果，分别在负载为30 N·m和40 N·m情况下，经过两种方法处理的效果与20 N·m时效果一致，最终出现周期为T的冲击脉冲。

图3　负载20 N·m 处理前后对比Fig.3　Compared before and after processing as the load is 20 N·m

图4　负载30 N·m 处理前后对比Fig.4　Compared before and after processing as the load is 30 N·m

行星齿轮箱正常运行时所采集的原始扭振信号往往是一个非稳定、非线性、多内容等复杂信号。H-P滤波相当于一个竞争性趋势估计算法，能够有效地保留故障扭振信号，使扭振信号趋于平稳并呈现出局部分段线性特征，该信号相对于原始信号时域波形更加简单，有效信号集中保留下来了，其脉冲冲击周期逐渐显现出来。然而，经过H-P滤波后的扭振信号为多内容的复杂信号，是具有不同成分的信号，VMD能将一个信号进行多层次分解，得到不同成分的模态分量，进一步简化信号，突出行星齿轮故障特性，再次经过VMD处理后的扭振信号其脉冲周期明显显现，故障诊断效果较好。

图5　负载40 N·m 处理前后对比Fig.5　Compared before and after processing as the load is 40 N·m

表3为不同扭矩下的周期和频率，从表中可看出其频率f几乎与行星齿轮故障频率fp相同，证实了该方法的可行性，因此，断定行星齿轮出现故障，与之前设置的故障类型一致，由此可见本研

表3　不同扭矩下的T与fTable 2　T and f under different torques

究所采用的故障诊断方法能有效地提取故障特性，从而诊断出设备故障。

4　结论

1) 将H-P滤波运用到行星齿轮箱故障诊断领域，并且对扭振信号的滤波效果明显。

2)对于行星齿轮箱故障冲击特征提取，提出了H-P滤波与VMD相结合的扭振时域分析方法。该方法对多内容复杂的扭振信号故障特征提取效果明显，通过不同负载下扭振信号分析，对比处理前后的时域图，均能提取脉冲冲击周期，验证了该方法的有效性。对实际工程中复杂的扭振信号，该方法具有较强的实用性，为故障诊断提供了一种有效的途径。

[1] 丁闯,江鹏程,张兵志,等. LMD 和时频熵在行星齿轮箱状态监测中的应用[J]. 噪声与振动控制,2016,36(6):154-157.

[2] 冯志鹏,褚福磊. 行星齿轮箱故障诊断的扭转振动信号分析方法[J]. 中国电机工程学报,2013,33(14):101-106

[3] 雷亚国,汤伟,孔德同,等. 基于传动机理分析的行星齿轮箱振动信号仿真及其故障诊断[J]. 机械工程学报,2014,50(17):61-68.

[4] 袁静,魏颖,訾艳阳,等. 自适应多小波混合构造方法及在故障诊断中应用[J]. 振动与冲击,2016,35(23):6-13.

[5] 李志农,朱明,褚福磊,等. 基于经验小波变换的机械故障诊断方法研究[J]. 仪器仪表学报,2014(11):2423-2432.

[6] 刘长良,武英杰,甄成刚. 基于变分模态分解和模糊C均值聚类的滚动轴承故障诊断[J]. 中国电机工程学报,2015,35(13): 3358-3365.

[7] Hodrick R J, Prescott E C. Postwar U.S. business cycles: an empirical investigation[J]. Social Science Electronic Publishing,1997,29(1):1-16.

[8] 冯志鹏,褚福磊. 行星齿轮箱故障诊断的幅值解调分析方法[J]. 中国电机工程学报,2013,33(8):107-111.

[9] 秦磊,谢邦昌. L1和L2分位数趋势滤波及其集成方法[J]. 数理统计与管理,2015,34(3):442-451.

[10] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing,2014,62(3):531-544.

[11] Wang Y, Markert R, Xiang J, et al. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system[J]. Mechanical Systems and Signal Processing,2015,60-61:243-251.

[12] 白堂博,张来斌,唐满红,等. 基于VMD的旋转机械故障诊断方法研究[J]. 石油矿场机械,2016,45(8):22-27.

[13] 冯志鹏,赵镭镭,褚福磊. 行星齿轮箱齿轮局部故障振动频谱特征[J]. 中国电机工程学报,2013,33(5):119-127.