磁流变阻尼器修正的Dahl模型的建立及仿真验证

苗　壮，龙海洋，李耀刚，楚　京，张　硕，叶晓蒙

(华北理工大学 机械工程学院，河北　唐山　063210)

0　引言

磁流变(MR)阻尼器因其拥有响应快、阻尼可控等优点，在汽车减振、建筑防震控制领域得到广泛应用。建立准确的力学模型是研究MR阻尼器振动控制的关键，常用的模型有Sigmoid模型、Bouc-Wen模型、现象模型、非线性双黏性模型、多项式模型等[1]。在力学模型的参数辨识问题上，学者们进行了大量研究[2]，禹见达等[3-4]采用了遗传算法进行参数辨识，王修勇[5]在参数辨识中采用了粒子群算法，张建明[6]采用了最小二乘法完成了参数辨识。

本文将对某款MR阻尼器建立修正的Dahl模型，通过力学性能试验采集到数据，并通过MATLAB Simulink中的参数估计工具对修正的Dahl模型进行参数辨识，然后将辨识出的参数导入模型进行仿真，将仿真结果与试验得到的数据进行对比，验证所建立的修正的Dahl模型的准确性。

1　修正的Dahl模型

修正的Dahl模型由Bouc-Wen模型发展而来，形式上相当于将Bouc-Wen模型中的Bouc-Wen单元替换为Dahl单元。如图1所示，修正的Dahl模型采用Dahl单元来模拟库伦摩擦力。与Bouc-Wen模型比较，不仅减少了待辨识的参数个数，与此同时还能很好地描述MR阻尼器的滞回特性。

输出的阻尼力的表达式如下：

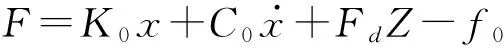
(1)

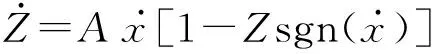
(2)

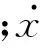
C0=C0s+C0dI.

(3)

Fd=Fds+FddI.

(4)

其中：C0s、C0d为C0和I的线性关系系数；Fds、Fdd为Fd和I的线性关系系数。

图1　修正的Dahl模型

2　磁流变阻尼器力学试验

本次力学性能试验的测试对象为美国洛德公司的RD-8041-1型MR阻尼器，试验所采用的仪器为杭州亿恒科技生产的阻尼器振动试验系统。

此次试验中，加载方式为正弦波激励，加载的电流分别是0 A、0.3 A、0.6 A和0.9 A，加载频率分别为0.5 Hz、1.0 Hz，1.5 Hz和2.0 Hz，振幅分别为5 mm、10 mm和15 mm。采用固定两项参数，改变第三项参数的方式，共进行了48种工况下的试验。MR阻尼器的活塞与缸体间的相对位移和输出阻尼力由相应传感器实时测量。

激励频率为1.5 Hz、振幅为15 mm时，电流为0 A、0.3 A、0.6 A、0.9 A四种工况下测得的实时阻尼力—速度和阻尼力—位移曲线如图2、图3所示。由图2、图3可知：阻尼力—位移曲线呈近似方形，阻尼力—速度曲线呈现明显的滞回特性;同样振动位移或速度情况下，电流越大，阻尼力越大。

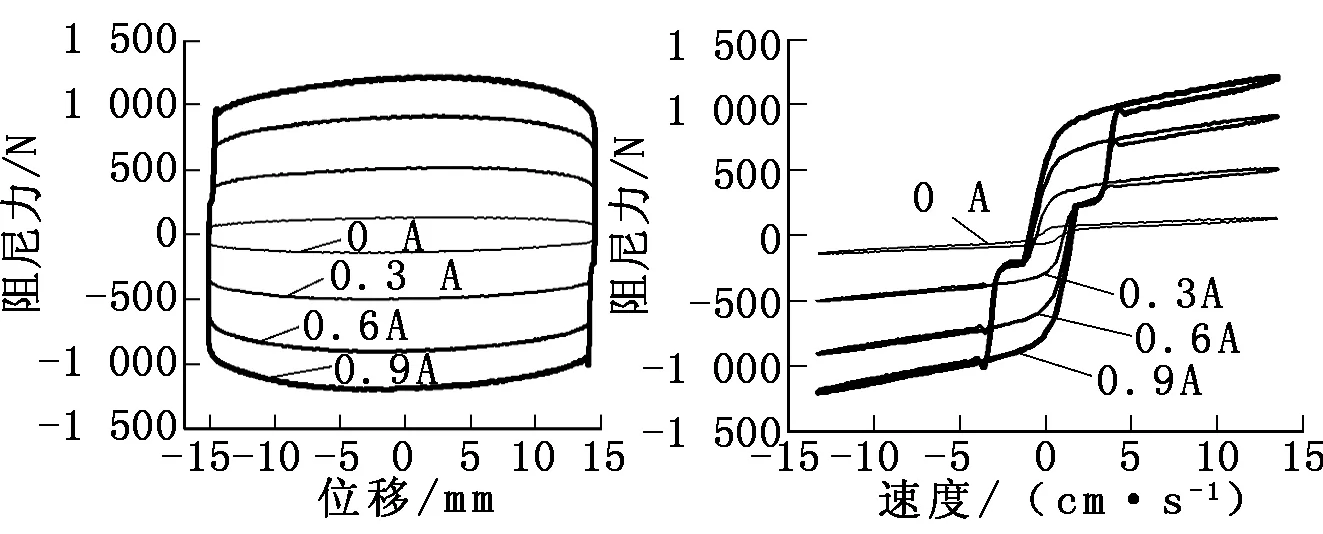
图2阻尼力—位移曲线图3阻尼力—速度曲线

3　修正的Dahl模型参数辨识

首先利用式(1)、式(2)在MATLAB Simulink中搭建MR阻尼器的修正的Dahl模型，如图4所示；然后打开Simulink中的Parameter Estimation参数估计工具，将试验中频率为1.5 Hz、振幅为15 mm时，四种不同电流下测得的位移、速度、阻尼力实时数据分批导入。其中，输入为位移和速度，输出为阻尼力。

图4　Simulink中建立的修正的Dahl模型

首先要辨识的参数为不同电流下的C0、K0、Fd、f0、A，并给定初始值为：C0=1.8 Ns·mm-1；A=42 s·mm-1；f0=0 N；Fd=95 N；K0=0.04 N·mm-1。辨识方法均选用参数估计工具中提供的最小二乘法，以0.3 A辨识过程为例，阻尼力拟合结果如图5所示。

图5　阻尼力拟合结果

由图5可知，阻尼力拟合曲线与原数据曲线吻合度较高，满足精度要求。四种电流工况下各参数的辨识结果如表1所示。

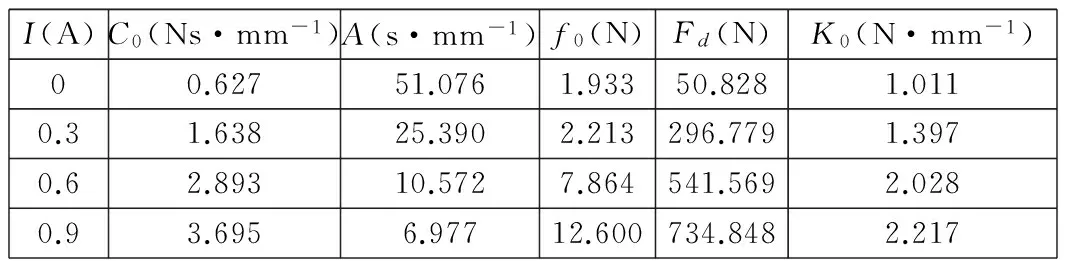
表1　各参数辨识结果

由表1可以看出，各参数均随电流变化而变化。在进一步描述参数与电流关系时，若全部参数均考虑在内，固然能提高力学模型精度，但会增加参数个数，增大辨识复杂度。选取对阻尼力大小和滞回特性影响较小的A、f0、K0三项参数，视其在变电流情况下仍为定值，对三者均取平均值，如表2所示。

固定A、f0、K0后重新对各电流下的Fd、C0进行辨识，并确定Fd、C0与电流I的关系。固定I、f0、K0后重新辨识的各电流下的Fd、C0如表3所示。

利用MATLAB对Fd、C0和电流的关系进行拟合，拟合后得出结论：Fd、C0随电流变化均呈如式(3)、式(4)所示的一次线性关系。C0d、C0s、Fdd、Fds辨识结果如表4所示。

表2　A、f0、K0辨识结果平均值

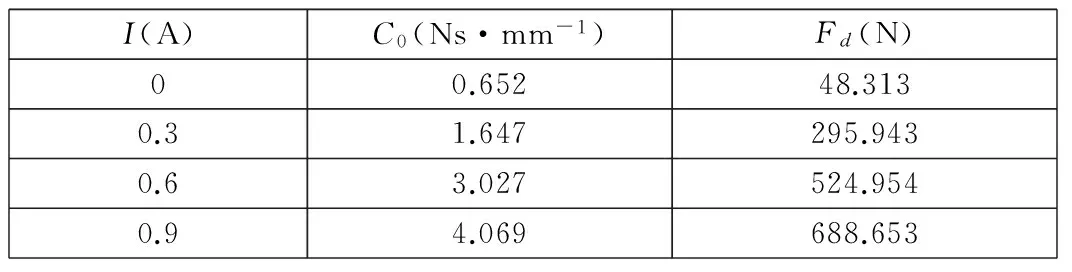
表3　Fd、C0辨识结果

表4　C0d、C0s、Fdd、Fds辨识结果

至此，参数全部辨识完成，表2和表4所示即为该MR阻尼器修正的Dahl模型的全部七项参数。

4　模型验证

在MATLAB Simulink中搭建引入电流因素的修正的Dahl模型，并将正弦信号作为激励，如图6所示。该激励频率为1.5 Hz，振幅为15 mm，并将辨识出的参数导入该模型进行仿真，得到仿真出的实时速度、位移、阻尼力。

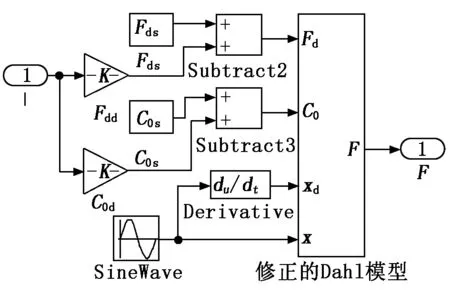
图6　引入激励的修正的Dahl模型

以电流0 A和0.6 A两种工况为例，对比仿真结果与试验结果。图7、图8分别为电流在0 A和0.6 A时的速度—阻尼力仿真结果与试验结果对比。

图7　I=0 A时速度-阻尼力仿真与试验结果对比

图8　I=0.6 A时速度-阻尼力仿真与试验结果对比

观察图7、图8可知，仿真值曲线与试验数据曲线基本吻合，同时仿真值曲线很好地描述了MR阻尼器的滞回特性。证明本文所建立的MR阻尼器的修正的Dahl模型准确有效，能很好地描述该MR阻尼器的力学性能。

5　结语

本文首先对RD-8041-1型磁流变阻尼器进行力学试验，采集到不同工作条件下的实时力、速度、位移数据，然后在Simulink中搭建磁流变阻尼器的修正的Dahl模型，并利用试验数据通过Simulink中的Parameter Estimation参数估计工具对修正的Dahl模型的参数进行了辨识。最后将辨识出的参数导入模型进行仿真，仿真结果与试验结果吻合度较高，并能很好地描述磁流变阻尼器的滞回特性。证明本文所建立的修正的Dahl模型准确，为进一步研究磁流变阻尼器的振动控制奠定了基础。

参考文献：

[1]李占卫,李治军.磁流变阻尼器动力学模型的研究现状[J].机械制造与自动化,2012,41(1):142-145.

[2]Peng G R, Li W H,Du H,et al. Modelling and identifying the parameters of a magneto-rheological damper with a force-lag phenomenon[J].Applied Mathematical Modelling,2014,38(15-16):3763-3773.

[3]禹见达, 陈政清, 王修勇,等. 基于遗传算法的磁流变阻尼器模型参数识别[J].地震工程与工程振动, 2009, 29(1):135-138.

[4]廖英英,刘永强,刘金喜,等.MRD模型参数识别及其在振动控制中的应用[J].振动、测试与诊断,2012,32(2):223-228.

[5]王修勇,龚禹,孙洪鑫,等.磁流变阻尼器滞回参数模型研究[J].土木工程学报,2014(增刊1):113-117.

[6]张建明,周传勇.基于最小二乘法的Bouc-Wen模型参数辨识[J].科技创新导报,2013(6):150-151.