半潜式海洋钻井平台DP系统滑模控制器设计研究*

梁　浩，赵东亚，赵　通

(1.中国石油大学(华东)化学工程学院,山东　青岛　266580； 2.北方信息控制研究院集团有限公司,江苏　南京　211153)

0　引言

半潜式海洋钻井平台动力定位(Dynamic Positioning，DP)技术，是利用自身推进器来抵抗环境因素如风、浪、流等干扰，保持海洋钻井平台的位置和航向，最终使其以固定的位姿状态保持在目标井口上方海面的某一最佳钻井位置[1-2]。

最初DP系统采用经典PID控制算法，对平台的纵荡、横荡和艏摇三个方向上的自由度分别实施控制，控制策略较为简单，但存在响应速度较慢、使用滤波器降低了精度、PID参数难以选择的问题。Balchen[3]等学者提出改进的线性二次高斯型(LQG)控制算法，在节约能源、稳定性、鲁棒性能上有较大优势，控制精度和响应速度方面性能较佳，但存在模型不够精确、计算量过大的问题。Landau[4]等学者提出模型参考自适应(MRAC)控制策略，实现容易、自适应速度快，缺点是其控制系统缺乏记忆性且不适用于强非线性系统。Ashrafiuon[5]等通过实验分析，验证了DP系统滑模控制的有效性和优越性。杜佳璐[6]等学者应用反步法控制算法，通过构造虚拟的控制器，求解带有不确定性系统问题较为容易，但对于强非线性和高阶的复杂问题，虚拟控制器很难设计。

滑模控制器自身具备很强的鲁棒特性，对系统不确定性和外部环境干扰具有较强的抑制能力，对复杂非线性系统具有较好的控制性能。因此，在充分考虑外部环境因素如风、浪、流等干扰的基础上，本文分别设计了线性滑模和两种终端滑模控制策略[7]。

1　问题描述

半潜式海洋钻井平台示意图如图1所示，半潜式海洋钻井平台的动力定位系统如图2所示，地球坐标系和平台坐标系如图3所示。

图1半潜式海洋钻井平台示意图图2半潜式海洋钻井平台动力定位系统图3地球坐标系和平台坐标系

图3中，在地球固定坐标系XEYEZE中，海洋平台位置为(x,y)，艏摇角度为Ψ，平台的位置向量为η=[x,y,Ψ]T。在平台坐标系XYZ中，速度向量V=[u,v,r]T，分别代表平台的纵荡、横荡以及艏摇速度。原点取在海洋平台的中心线上，地球固定坐标系与平台坐标系的转化关系及平台非线性动力学方程如下：

(1)

(2)

其中：J(Ψ)为雅可比矩阵；M,D∈R3×3分别为惯性矩阵和线性阻尼矩阵。τ∈R3×1为纵荡、横荡方向的控制力及艏摇方向的控制力矩；d∈R3×1为风、浪、流干扰及未建模动力学特性。

假设d0为干扰及不确定性的上界，满足:

‖d(t)‖0.

(3)

在本文中，假设平台足够稳心稳定，雅可比矩阵可以用于描述运动方程，即：

(4)

J(Ψ)对于所有Ψ均是非奇异的，有：

(5)

联立式(1)和式(2)，整理得到：

(6)

为了对式(6)进行简化，令:

(7)

则式(6)可以简化为：

(8)

2　滑模控制器设计及稳定性证明

由式(8)可得：

(9)

在此进行如下假设：①式(9)中，d代表外部干扰，且有‖d‖≤d0，d0>0为正常数，即d有界；②因为M可逆、J可逆，那么P=MJ-1可逆；③系统状态x1和x2均可测。

2.1　线性滑模控制器设计

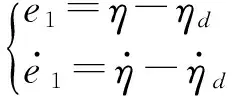
(10)

定义线性滑模S1如式(11)所示：

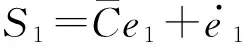
(11)

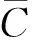
设计滑模控制律为：

(12)

其中：κ1>0，ζ1>0，均为控制器参数；‖·‖代表向量的范数。

为了避免抖振，控制律τ11可以重新设计成：

(13)

其中：δ1为所取边界层范围。

证明1：定义Lyapunov函数为：

(14)

则有：

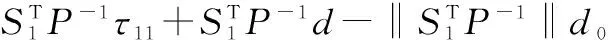
由式(15)可知，误差e1将在有限时间内到达滑模面S1，并将沿滑模面收敛到零点。

2.2　终端滑模控制器设计

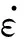
(16)

跟踪误差的动力学方程如式(17)所示：

(17)

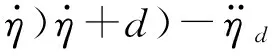
(18)

定义终端滑模S2(TSMC1)如式(19)所示：

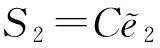
(19)

其中：C为增益矩阵，定义如下：

(20)

其中：cii>0,i=1，…，n。

一般情况下，p1和p2是正奇数且满足以下两个条件：

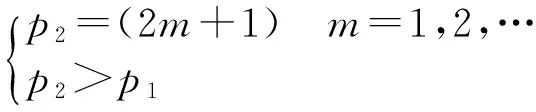
(21)

多输入多输出系统的终端滑模函数如式(22)所示：

(22)

(23)

设计终端滑模控制律为：

τ2(t)=τ20+τ21+τ22.

(24)

(25)

.

(26)

τ22=-κ2P(CB)-1S2.

(27)

证明2：定义Lyapunov函数为：

(28)

则有：

‖ST‖‖CBP-1‖(d0-‖d‖)≤0.

(29)

由式(29)可知，误差e2能够在有限时间内到达滑模面S2，并沿着滑模面收敛到零点。

2.3　新型终端滑模控制器设计

(30)

定义终端滑模S3(TSMC2)如式(31)所示：

(31)

其中：sig(e3)α=[|e31|αsgn(e31),…，|e3n|αsgn(e3n)]T，sgn(·)为符号函数，n为向量的维数；λ为滑模增益系数矩阵；α为终端滑模指数项系数。

设计终端滑模控制律为：

τ3(t)=τ30+τ31.

(32)

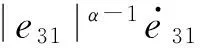
(33)

(34)

同理，为了降低抖振，τ31重新设计为：

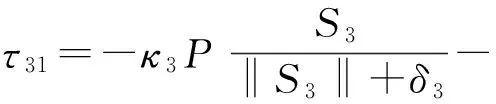
(35)

其中：κ3>0，ζ3>0，均为控制器参数；δ3为所取边界层范围。

证明3：定义Lyapunov函数为：

(36)

则有：

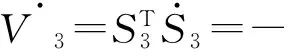
‖d‖)≤-κ‖S3‖≤0.

(37)

由式(37)可知，误差e3能够在有限时间内到达滑模面S3，并沿滑模面收敛到零点。

3　仿真验证及分析

为验证所设计观测器和控制器的有效性，对半潜式海洋平台动力定位过程进行仿真研究。动力学参数矩阵和环境干扰分别为：

.

.

d=[50sint，50sint,50sint]

.

控制器参数设置如表1所示，仿真时间T=15 s，为验证控制系鲁棒性，在7 s≤t≤7.1 s施加给三个控制系统相同的脉冲干扰f：

.

图4～图9为设定点三种滑模控制的追踪曲线。

图4纵荡方向位置曲线图5横荡方向位置曲线图6艏摇方向角度曲线

图7纵荡方向控制输入图8横荡方向控制输入图9艏摇方向控制输入

图4～图6是x、y、Ψ三个方向的追踪曲线，由图分析可得，TSMC2的响应最快，其次是TSMC1，SMC控制响应最慢。当对系统施加外界干扰f时，TSMC2产生的振荡幅值较小，TSMC1其次，SMC振荡幅值最大。经过一段时间，系统重新恢复稳态，TSMC2所需时间最短，TSMC1其次，SMC所需时间最长。因此，从系统响应速度和鲁棒性分析，控制效果TSMC2>TSMC1>SMC。

4　结论

本文以海洋钻井平台的动力定位系统为研究对象，在系统位置信号和速度信号均可测量的假设条件下，提出了线性滑模控制策略和两种终端滑模控制策略。运用Lyapunov方法从理论上证明了系统的稳定性，并通过仿真模拟试验验证了三种控制器的有效性，能够实现平台的定点控制。最后，将三种控制器的控制效果进行比较分析，从系统的响应速度、鲁棒性和抗干扰特性三个方面进行综合对比，控制效果TSMC2>TSMC1>SMC。该研究结果对于海洋钻井平台动力定位系统具有一定应用价值及现实意义。

参考文献：

[1]Srensen A J.A survey of dynamic positioning control systems[J].Annual Reviews in Control,2011,35(1):123-136.

[2]余培文,陈辉,刘芙蓉.船舶动力定位系统控制技术的发展与展望[J].中国水运,2009(2):44-45.

[3]Balchen J G,Jenssen N A,Mathisen E,et al.Dynamic positioning of floating vessles based on Kalman filtering and optimal control[C]//IEEE Conference on IEEE.[s.l.]:IEEE,1980:852-864.

[4]Landau I.A generalization of the hyperstability conditions for model reference adaptive systems[J].IEEE Transactions on Automatic Control,1972,17(2):246-247.

[5]Ashrafiuon H,Muske K R,Mcninch L C,et al.Sliding-mode tracking control of surface vessels[J].IEEE Transactions on Industrial Electronics,2008,55(11):4004-4012.

[6]杜佳璐,李文华,郑凯,等.船舶动力定位系统的非线性输出反馈控制[J].华南理工大学学报(自然科学版),2012,40(2):70-75.

[7]Zhao D,Li S,Zhu Q.Output feedback terminal sliding mode control for a class of second order nonlinear systems[J].Asian Journal of Control,2013,15(1):237-247.