管件弯曲工艺参数对截面质量影响有限元模拟*
2018-04-02叶小奔
向 明, 叶小奔
(1.大连理工大学 机械工程学院,辽宁 大连 116024; 2.景德镇陶瓷大学 机械电子工程学院,江西 景德镇 333001)
0 引 言
大口径船用管件多采用冷弯成形工艺,GB/T 28763—2012中规定圆度≤8%,减薄率≤12%。
管件弯曲成形中存在外侧减薄甚至破裂、内侧增厚甚至起皱、横截面圆度超差等问题。管件产品主要检测项有管件减薄、截面圆度及褶皱度。针对管件弯曲成型的质量问题,国内外学者们主要采用有限元模拟进行研究。李强[1]采用有限元模拟TBLU7数控弯管机弯曲的过程,验证了TBLU7数控弯管机满足设计要求。徐建美[2]等采用ABAQUS对0Cr21Ni6Mn9N不锈钢管材进行有限元弯曲模拟,分别得到了芯棒、弯曲模、压块的间隙等工艺参数对管件弯曲质量的影响规律。许小妹[3]等采用ABAQUS对0Cr21Ni6Mn9N不锈钢管材进行有限元弯曲模拟,研究了芯棒伸出量对减薄、截面圆度的影响规律。余胜娟[4]等采用有限元法对圆形钢管弯曲成形过程进行模拟,指出了滚珠的间隙及滚珠角速度等对管材成形的影响规律。Miller J E[5]等人采用理论分析,建立曲面的弯曲变形理论研究加载对铝材矩形管拉弯截面变形的影响。夏东强[6]通过有限元方法研究了材料参数、相对弯曲半径以及壁厚等对弯管减薄和截面圆度的影响规律。刘启骞[7]通过有限元模型分析了管壁厚度、管材直径和变形程度对成形件截面圆度的影响。王光祥[8]等建立有限元模型,研究了薄壁管弯曲工艺参数对弯管外侧拉裂、内侧褶皱及截面圆度等管件截面质量参数的影响规律。本文利用有限元模拟大口径船用20钢管件数控弯曲成形过程,获取芯棒伸出量、芯棒间隙工艺参数对弯管截面质量的影响规律,为船用管件弯曲成形工艺参数选取提供依据。
1 弯管过程约束与载荷分析
1.1 弯管机动作简介
图1为弯管机装配图。管件加工过程如下:管件双眼正安装在小车卡盘上,开始弯曲时小车进给移动管件末端身长量至第一个起弯点,前卡与胎模一起旋转进行第一次弯管,前卡与胎模的旋转角度称为曲角;小车进给至第二个起弯点,进行第二次弯曲,如果是空间管件,卡盘旋转角度,管件末端旋转至空间位置,称卡盘旋转角为转角,然后前卡胎模旋转进行管件弯曲,这样依次动作完成管件弯曲。
1.2 模拟设置
本文所研究的管件是Φ114 mm×6 mm的厚壁管,建立如图2所示的管件数控弯曲成形模型。
图2是船用管件弯曲成形水平投影图。胎膜5绕Z轴转动,前卡1随胎膜5回转;前卡1与镶块6带动管件2前端随胎膜5一起旋转;压板3与管件弯曲后端一起随动。模拟过程约束情况见表1。
1.3 实验获取材料属性
管件采用壳体单元,采用5个积分点计算,管件厚度按实际值6 mm。刚体材料厚度设为20 mm,采用5个积分点计算。管件的弹塑性模型由实验得到,实验采用d0=10 mm的圆形截面定标距试样,实验设备采用电子万能试验机,实验温度为室温,缓慢加载直到拉伸试样断裂,记录屈服强度、抗拉强度及载荷—位移曲线。通过多次拉伸试验,得到普通船用20钢管的材料属性,如表2所示。
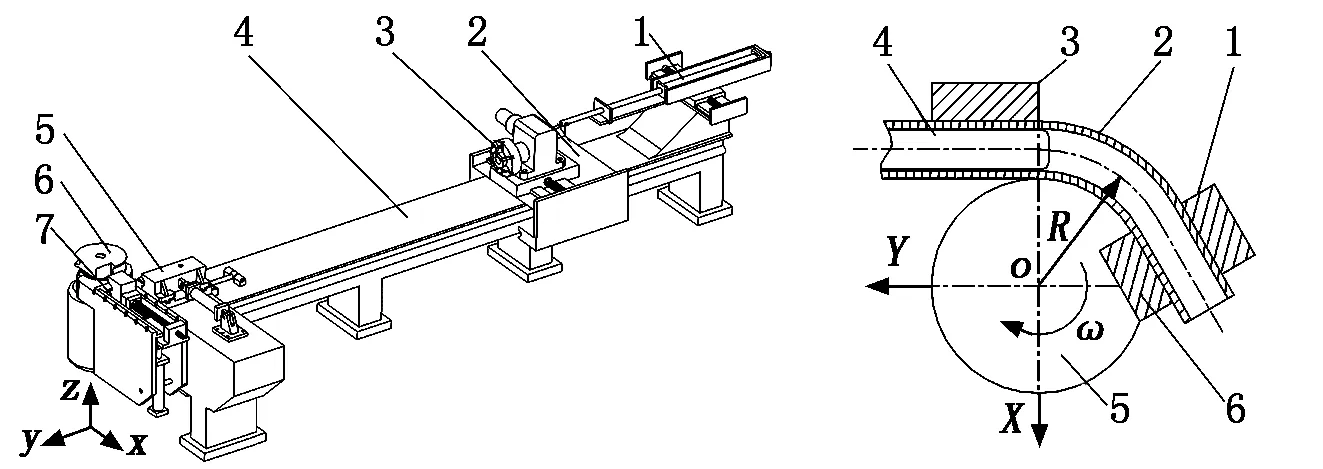
1-尾座;2-小车;3-卡盘;4-床身; 1-前卡;2-管件;3-滑板组;5-滑板组;6-主轴胎模;7-前卡4-芯棒;5-胎膜;6-镶块
图1弯管机装配图图2管件弯曲成形模型

表1 模拟材料和约束设置

表2 管件材料的性能参数
考虑到模型在ABAQUS有限元软件后处理过程中运算时间等因素,于是模型中的胎膜、芯棒、前卡、镶块及滑板均定义为刚体。
2 船用管件弯曲成形模拟
通过网格灵敏度分析,管件网格大小选为10 mm。划分网格的管件弯曲有限元模型如图3所示。
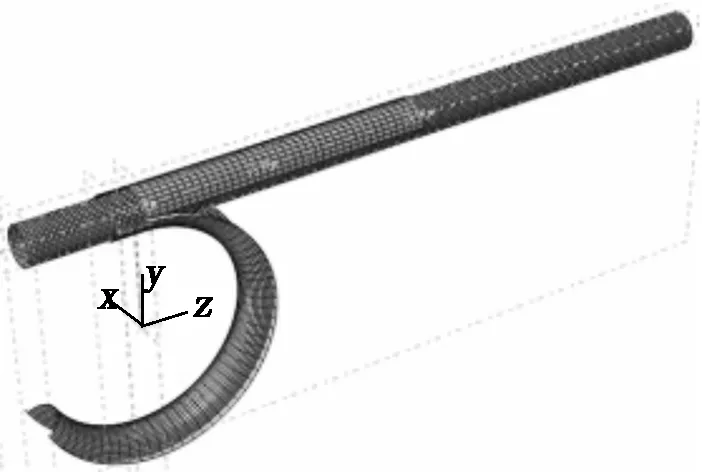
图3 弯管成形有限元模型
从起弯点开始采样,沿管件方向每隔50 mm均匀设置23个采样点。对弯曲胎模刚体施加RZ定值角速度,弯管成形过程中壁厚变化分布云图如图4所示。从图4可知:船用管件在弯曲成形中,外侧出现减薄现象,内侧出现壁厚增加现象;在弯曲0°~30°角度时,内外侧壁厚变化较快,在弯曲30°~180°时,内外侧壁厚变化维持在稳定状态。
减薄率随弯曲角度的变化如图5所示。由图5可知,随弯曲角度的增大外侧减薄最大值基本不变。
截面畸变程度(圆度值)随弯曲角度的变化如图6所示。由图6可知,管件弯曲区域截面圆度变形最大值随弯曲角度的增大而增大。这是因为在变形前期变形区域离芯棒距离较近,芯棒支撑是充分的,随着弯曲角度的增大,变形区远离芯棒,缺乏芯棒支撑,从而导致截面畸变程度增大。
3 最佳工艺参数选取模拟分析
管件数控弯曲是一个复杂成形过程,受诸多工艺参数和外界约束因素影响,在这些影响因素中,较容易实现调节的工艺参数有芯棒伸出量、芯棒与管件间隙两个工艺参数,本文通过有限元模拟,改变芯棒伸出量、芯棒与管件间隙获取管件截面质量值,从而获取合适的工艺参数范围,以供实际管件弯曲成形工艺使用。
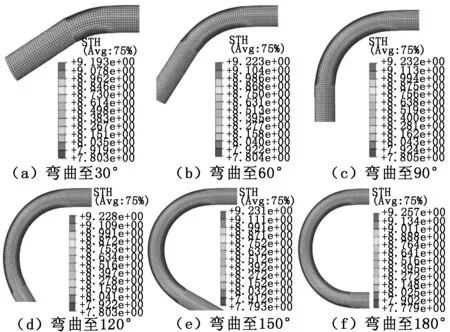
图4 弯管成形过程中壁厚变化分布云图
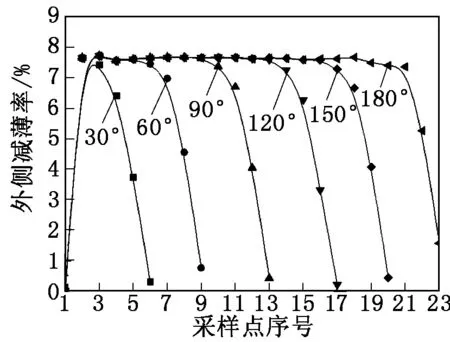
图5 减薄率随弯曲角度的变化
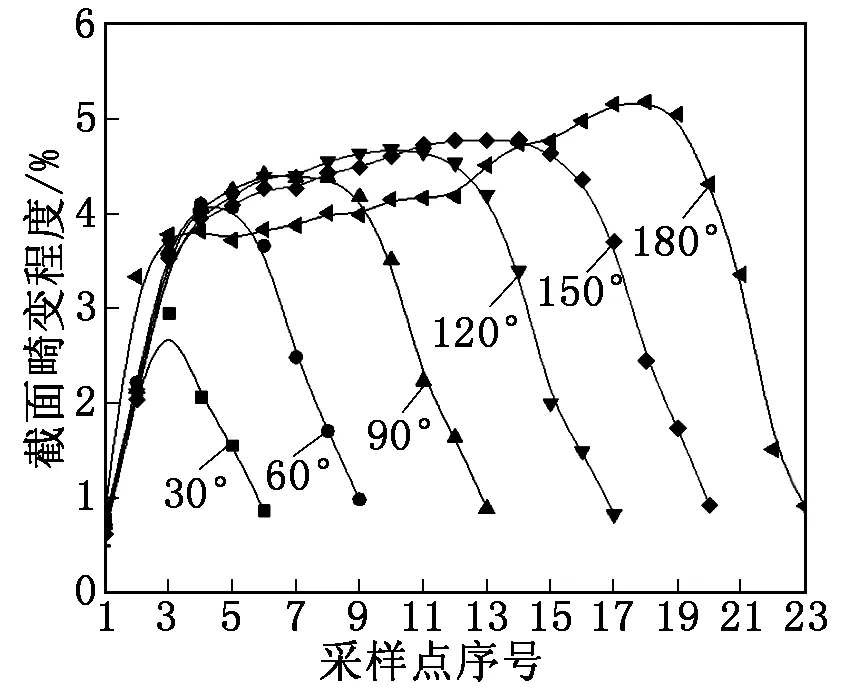
图6 截面畸变程度随弯曲角度的变化
3.1 芯棒伸出量的模拟分析
芯棒伸出量分别取20 mm、25 mm、30 mm、40 mm及50 mm,管件弯曲180°其他条件不变进行模拟,提取动作后的壁厚减薄率和圆度误差,如图7所示。
由图7(a)可知,随着芯棒伸出量由20 mm增加到50 mm,管件减薄率由6.91%变化为10.05%,最大减薄率由7.71%逐步增加为13.34%;当支撑芯棒伸出量达到50 mm时其最大减薄率已超出允许值10%(允许值参考GB/T 28763—2012)。由图7(b)可知,弯管截面圆度值随芯棒伸出值增加而相应地减小,圆度值由3.84%减小到1.07%,最大圆度值由5.18%减小到2.04%;当伸出量达到50 mm时其截面圆度值出现负值。
从上述模拟可知芯棒伸出量对圆度和减薄率的影响:减薄率随芯棒伸出而加大,最大值为13.34%,这是由于芯棒对外侧变形区域的应力造成的;而圆度值随芯棒伸出量增加而减低,说明芯棒伸出值越长对管件圆度变形越有抑制作用;当芯棒伸出值为20 mm时,圆度值超出允许值5%(允许值参考GB/T 28763—2012),当芯棒伸出量为40 mm、50 mm时减薄率最大值为10.04%和13.34%,也超出允许值。所以综合两项管件截面质量指标,确定芯棒伸出量最佳取值在25 mm~30 mm。
3.2 芯棒与管件之间间隙的模拟分析
芯棒与管件内侧单侧间隙分别取0.5 mm、1 mm、2 mm、3 mm及4 mm,管件弯曲180°其他条件不变进行模拟,提取动作后的壁厚减薄率和圆度误差,如图8所示。
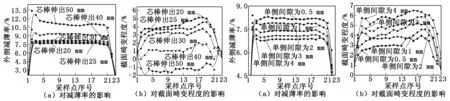
图7芯棒伸出量对截面质量的影响图8芯棒与管件的单侧间隙对截面质量的影响
由图8(a)可知,随着芯棒与管件内侧单侧间隙由0.5 mm增加到4 mm,减薄率由7.45%减小到6.25%,最大减薄率由8.38%减小到7.49%。由图8(b)可知,弯管截面圆度值随芯棒与管件内侧单侧间隙增加而相应地增加,圆度值由3.98%增大到6.49%。
从上述模拟可知芯棒与管件内侧单侧间隙对圆度和减薄率的影响:减薄率随芯棒间隙增大而减小,最小值为6.25%,这是由于芯棒对外侧变形区域的应力减小造成的;而圆度值随芯棒间隙增加而加大,说明芯棒间隙越大,芯棒对管件圆度变形抑制作用越小;当芯棒间隙为2 mm时,圆度值超出允许值5%。所以综合两项管件截面质量指标,确定芯棒间隙最佳取值在0.5 mm~1 mm。
4 结论
本文通过实验获取材料属性,通过ABAQUS模拟分析,研究了芯棒伸出量、芯棒与管件单侧间隙两个工艺参数对船用管件数控弯曲成形减薄率及圆度值的影响。通过模拟取得了减薄率及圆度值随这两个工艺参数的变化规律。通过分析可知:减薄率随着芯棒伸出量增加而加大,圆度值随着芯棒伸出量增加而减小,芯棒伸出量合适范围为25 mm~30 mm;减薄率随着芯棒与管件单侧间隙增加而减小,圆度值随着芯棒与管件单侧间隙增加而增加,芯棒与管件单侧间隙合适范围为0.5 mm~1 mm。
参考文献:
[1]李强. 虚拟样机技术在数控弯管机设计开发中的应用研究[D]. 昆明:昆明理工大学, 2007: 23-30.
[2]徐建美.基于有限元模拟的0Cr21Ni6Mn9N不锈钢管数控弯曲截面质量研究[D].南昌:南昌航空大学,2014:31-40.
[3]许小妹,鲁世强,等.芯棒伸出量对0Cr21Ni6Mn9N不锈钢管数控弯曲成形质量的影响[J].锻压技术,2014,39(5):73-77.
[4]余胜娟,周旭东.管材弯曲中外侧壁厚变化的数值模拟[J].锻压技术,2007,32(6):90-94.
[5]Miller J E,Kyriakides S,Corona E.On bend-stretch forming of alumium extruded tubes:analysis[J].International Journal of Mechanical Science,2001,43:1319-1338.
[6]夏东强.管材弯曲成型技术研究[D].重庆:重庆大学,2008:25-30.
[7]刘启骞.型材多点弯曲中的成形缺陷及其抑制方法的数值模拟研究[D].长春:吉林大学,2011:28-42.
[8]王光祥,杨合,李恒,等.工艺参数对薄壁数控弯管成形质量影响的实验研究[J].机械科学与技术,2005,24(8):995-998.
