基于遗传算法的射线箱机加车间机器人制造单元布置
2018-04-02高治理赵铁军王若刚张亦平
高治理,赵铁军,王若刚,张亦平
(1.沈阳工业大学 机械工程学院,辽宁 沈阳 110870;2.东北大学,辽宁 沈阳 110819)
0 引言
随着市场经济发展,消费者需求也随之发生变化,导致大批量生产向多品种小批量转变,除转变企业管理模式外,还要对设施布置优化。制造单元是柔性高、快速响应的小型制造系统,它将复杂且长的系统拆分成若干个制造单元[1]。制造单元布置兼具工艺布置的柔性高,设备通用化适应小品种多批量生产和产品布置生产效率高、成本低的特点,是大批量生产的效益和多品种小批量的灵活生产方式。随着自动化水平提高,企业的生产模式随之向机械手、加工中心、搬运机器人组成柔性制造单元模式转变,不仅提高了效率且代替人所不能参与的如劳动强度高、危险的生产活动,它把大批量制造的经济性和中小批量制造的灵活性有效的结合起来,得到了国内外学者关注。如,倪玉晋[1]提出发动机的机器人制造单元,以物流成本为目标利用遗传算法进行单行布局,提高企业产能;杨阔然[2]提出单元内及系统进行布局,以物流距离、成本多目标进行布局,提高生产效率;AS Tubaileh[3]提出以机器人运行时间为优化目标,利用模拟退火算法工具箱对制造单元进行布局规划,提高了物料输送效率。MS Sedehi[4]等提出以AGV单向距离最短,构建直线单行布局,提高了运行时间,利用启发式算法在Matlab中实现。
本文利用机器人对制造单元输送物料,提出以速度和访问频率为优化目标,时间、设备间距、加速度为约束,提高输送速度这是与以往将成本、距离作目标进行布置所不同的。将此法应用于C机械制造有限公司。
1 基于机器人的制造单元布局
1.1 制造单元布局思想
C公司生产的射线箱是医疗设备重要部件之一,属于多批量小品种生产模式。实行单元制造,射线箱共由8个零件构成,如表1所示,故将各零件封装组成8个机加单元C1~C8,单元内放置加工中心P1~P8组合(1台或2台)与上下料机械手,单元旁放置缓存区,形成两排成单行布置,由搬运机器人输送物料到缓存区,由机械手完成上下料。横向箭头仅代表该工序为1道工序
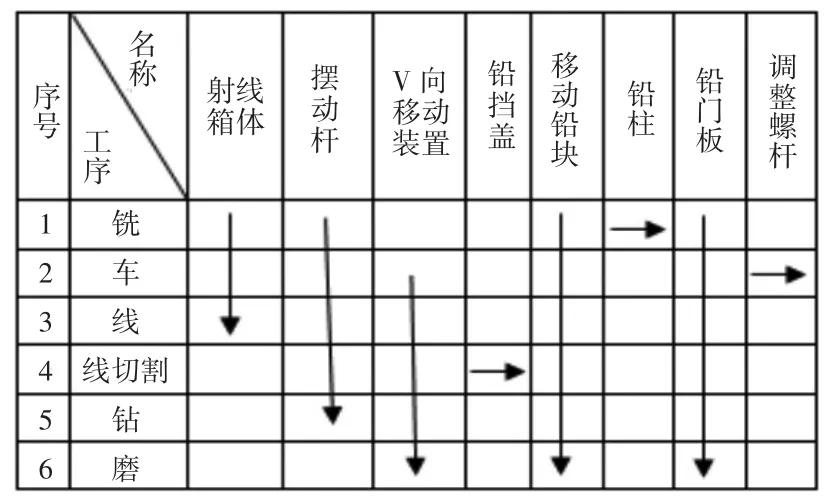
表1 射线箱机加工艺流程
1.2 机器人选型
选用移动式搬运机器人AGV,按预定路径往返于各个机加单元输送物料,单元内采用关节机械手。
1.3 机器人运动参数分析
机器人在平面沿着生产单元方向运动,运动状态描述如下:机器人在某生产单元(C1P1)开始保持静止状态,速度为零;以初始速度启动加速将物料搬运到另一个单元(CqPq),到达某一瞬时保持匀速直线运动,到达某一单元时,开始不断减速,进行慢行对位直至停止,循环重复上述运动,直到所有物料搬运完。基于此,定义机器人的运动参数,即起点速度(V0),起点加速度(as),等速直线速度(Vtraverse),终点加速度(ae),终点速度(Ve)和间隔时间(△t)[5],其中Vtraverse在本文定义为匀速直线速度(uniform straight line),简称 Vusl.
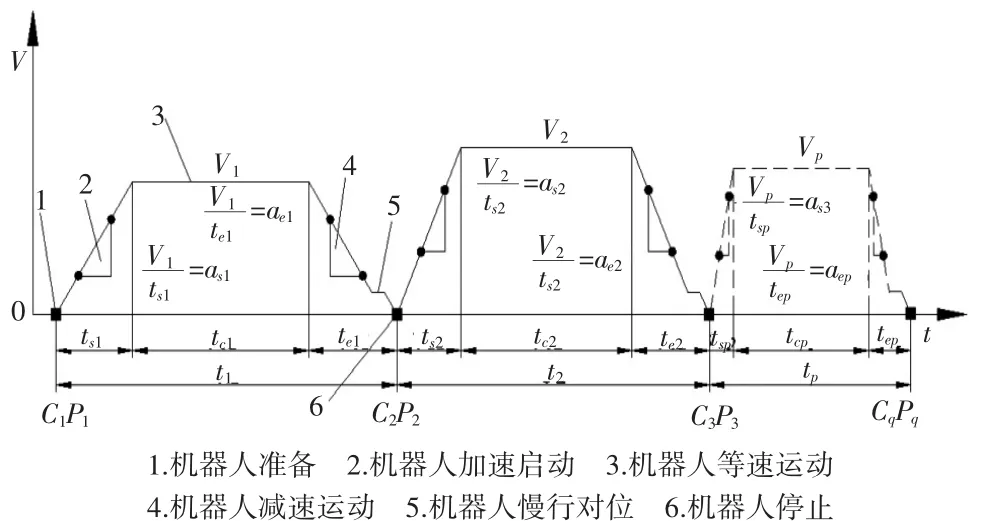
图 1 v、a、t分布关系
图1描述了机器人在某单元到另一单元起点、终点运动参数:
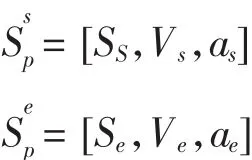
1.4 建立速度最优数学模型
1.4.1确立变量约束条件
从图1看出,机器人在从一个生产单元到下一个单元之间所需的速度Vp与时间tp分为3个阶段的速度间与时
间间隔:

式中,tep,asp是从起点为零的速度加速到匀速直线运动所需的时间与加速度,tcp是匀速直线运动速度Vp所需要的时间,tep,aep是从匀速直线运动减速到零的末端速度的时间与加速度。根据以上可以描述从一个生产单元i到下一个单元j的位置描述如下:

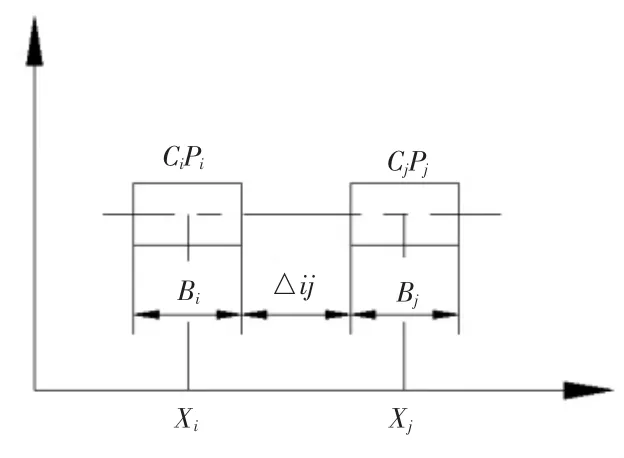
图2 单行布局示意图
其中,xi,xj为各个制造单元中心间距的x轴坐标,Bi,Bj分别为单元 CiPi,CjPj宽度,△ij为各个制造单元中心间距。同理机器人在i单元后的下一个单元,再从 j单元到后面的单元 j-1,j-2,…,j-n为了要在同一行程中多次访问生产单元,则j-n与的位置间的参数相同,所以对j单元到j-n单元位置描述如下:
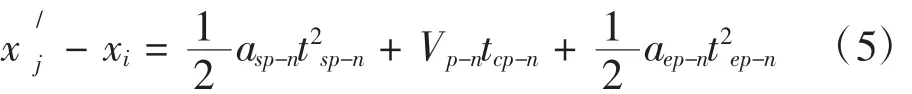
式中,tsp-n,asp-n是从起点为零的速度加速到匀速直线运动所需的时间与加速度,tcp-n是匀速直线运动速度Vp-n所需要的时间,tep-n,aep-n是从匀速直线运动减速到零的末端速度的时间与加速度。
控制变量为:(asp,asp-n,aep,aep-n,Vp-n,Vp,tsp,tcp,tep,tsp-n,tcp-n,tep-n)
用未知量X表示上述控制变量为:x=(x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11,x12)
1.4.2确立目标函数
考虑机器人在单行布局中在N个生产单元间进行物料搬运,为了及时将物料搬运到指定位置,机器人的运动速度至关重要,它决定物料的流动效率,应以速度最大为优化目标,来确立制造单元布置,建立模型如下:
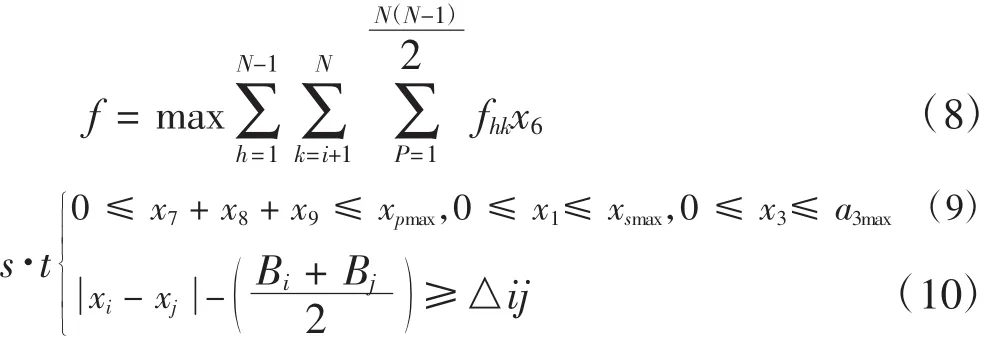
式中,f为优化单元h与单元k之间的访问频率,fhk与该行程所需的行驶速度的乘积,N为单元数,l为行数。公式9为速度与加速度约束,公式10防止单元间的重合或干涉。
2 基于MATLAB遗传算法工具箱求解
遗传算法是以自然选择和遗传理论为基础将生物进化工程中适者生存规则与群体内部染色体的随机信息交换机制相结合的高效全局寻优搜索算法[6]。MATLAB遗传算法工具箱由专门设计的遗传算法与直接搜索工具组成,在MATLAB R2008a以上版本中将二者合并到optimizationTOOL工具箱中,用于问题创建、适应度运算、选择、交叉和变异等,它可以处理难以定义或不便于进行数学建模的问题,在命令行中调用其GUI界面,支持M代码自动生成[7]。但遗传算法不具有约束函数的能力,所以必须将约束优化问题转化为无约束优化问题,对于等式和不等式的约束采用外点法惩罚函数从而转化为无约束优化[8]。其函数为:
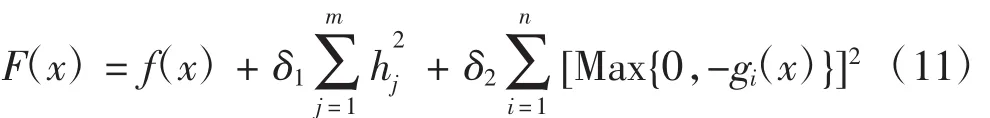
式中,hj为等式约束,gi为不等式约束,δ1δ2为惩罚函数,n,m为等式与不等式约束个数。
根据公式8确立等式与不等式约束,其中时间、速度、加速度最大值参数设定为12 s、3 m/s、1.5 m/s2:
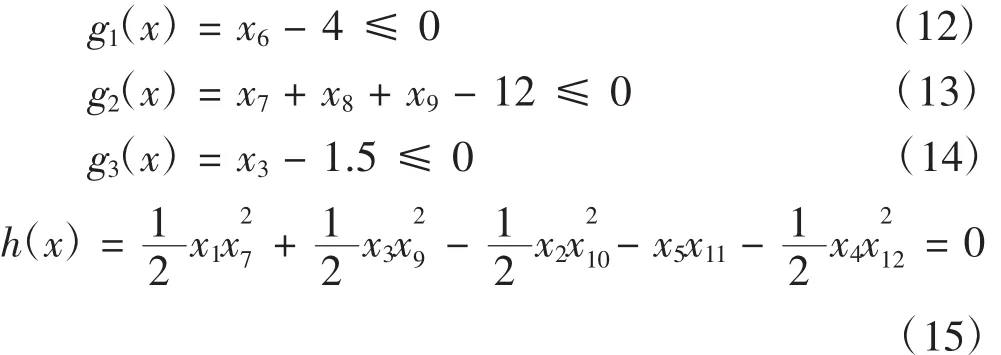
n取0~10,以便于在此范围内观察目标函数值得变化情况。单元之间访问频率和单元间矩阵如下(第1和2行):

设置迭代步数为100,变异概率为0.05,种群大小为40,交叉概率为0.6,设置变量为12.并将速度与时间结果调入自定义Plot曲线中,画出速度与时间曲线。经过7次迭代,结果趋于稳定,求出变量Xi(i=1-12)=5,4,2,3,5,4,3,6,2,4,4,3,最大速度VP=3 m/s,tP=12 s,并画出速度—时间关系曲线图,从而可对第一行制造单元布局,如图4.另一行制造单元布局步骤与第一个相同,不在赘述。需要注意的是每个制造单元尺寸考虑到电气布线、机械手作业半径等因素,长宽尺寸要比制造单元的净尺寸大2 mm.

表2 制造单元尺寸
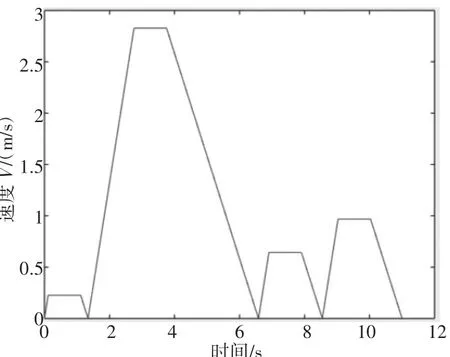
图3 排序为2-4-3-1的4个制造单元布局

图4 制造单元布局图
3 结论
本文将每个零件封装成制造单元,利用机器人进行物料输送,不同以往解决基于距离之间的布局问题,而是以速度最大化为目标建模,所提出的方法对基于机器人的多品种小批量单元式车间布置具有实际意义。
参考文献:
[1]倪玉晋.轿车发动机缸盖柔性精密制造单元总体结构设计与关键技术研究[D].南京:南京理工大学,2016.
[2]杨阔然.X公司机加车间单元布局设计研究[D].长春:吉林大学,2012.
[3]AS Tubaileh.Layout of flexible manufacturing systems based on kinematic constraints of the autono mous material handling system[J].International Journal of Computer Integrated Manu facturing.2014,74(9-12):1521-1537.
[4]MS Sedehi,RZ Farahani.An integrated approach to deter mine the block layout,AGV flow path and the location of pick-up/delivery points in single-loop systems[J].International Journal of Production.2009,47(10):3041-3061.
[5]Biagiotti L,Melchiorri C(2008)Trajectory planning for au tomatic machines and robots.Springer,Berlin.
[6]严寒冰,原思聪,季文祥.基于遗传算法及MATLAB的V带传动优化设计[J].机械,2008,19(5):23-25.
[7]雷英杰,张善文,李续武.MATLAB遗传算法工具箱及应用[M].西安:西安电子科技大学出版社,2005.
[8]段路茜,孙月海,王树人.基于MAGA一次包络TI蜗杆传动参数优化[J].中国机械工程,2008,19(5):531-53.
