基于人工鱼群算法的混凝土锯切力预测模型

陈 波 ，熊飞翔 ，王 艳

（1．广西大学 机械工程学院，广西 南宁530004；2.广西大学广西制造系统与先进制造技术重点实验室，广西 南宁530004）

0　引言

混凝土是用水泥、细骨料（如砂子）、粗骨料（如碎石、卵石）和水按一定比例配合搅拌后入模浇注，并经养护硬化后做成的人工石材，它是一种典型的脆硬材料。金刚石工具锯切混凝土拥有锯切时间短、精度高、噪音小、灰尘少和对环境的污染小等优点而得到广泛应用。在锯切混凝土过程中，锯切力反映了锯片所承受的载荷，并影响着锯片的使用寿命。

金刚石工具在锯切混凝土的过程中，由于混凝土材料的非均质多种材料混合特性及工具上有效磨粒数的动态变化情况异常复杂，要建立一个切合实际的加工过程模型非常困难。锯切力是加工过程模型重要的评价参数，为了从理论分析脆硬材料加工过程规律以便达到加工过程监控的目的，对锯切力进行理论建模是有效方法之一。胡映宁[1]等通过分析金刚石圆锯片在锯切过程中混凝土声发射信号和据切力信号特征，发现声发射信号的变化规律与锯切力信号的变化规律有较好的一致性。郑春英[2]采用回归分析方法建立了锯切力的数学模型，可以根据给定的参数来预测锯切力。LI Y.[3]等研究了硬花岗石深锯加工中的切削力，发现最大锯切深度可达120 mm，并用有限元法分析了锯片的应力分布，发现可以通过该方法对锯片进行优化设计。ZHANG Z.M.[4]等利用曲面响应法建立了金刚石圆锯片锯切花岗岩锯切力数学模型，发现工艺参数对锯切力的影响都是显著的。KARAKURT I.[5]等基于回归分析的方法对锯切力进行建模，发现该模型能有效地预测岩石锯切力。陈亚洲等[6]通过对金刚石锯片和切割参数的技术改进提出了一套金刚石锯切优化技术，这套技术在石材切割领域的技术转化设备中已经得到了实践和应用。郑冬锐[7]等用小波分析方法对采集到的信号进行分析测试，发现不同锯切工艺参数下切削力与声发射信号具有较好的同步对应性。从近年的研究来看，采用智能算法建立混凝土锯切力模型是可行的。

混凝土作为人造预制材料，其材料成分主要为河沙、石子及水泥。混凝土锯切力预测模型由于受到混凝土材料分布不均、材料脆性大塑形小等的影响，呈现与金属材料非常不同的特性。而国内外研究仍然使用传统切削力公式进行回归分析，其结果常常与实际加工情况大相径庭。

人工鱼群算法（Artificial Fish-Swarm Algorithm，AFSA）是由李晓磊[8，9]等在 2002年提出的，源于对鱼群运动行为的研究，是一种新型的智能仿生优化算法。它具有较强的鲁棒性、优良的分布式计算机制、易于和其他方法结合等优点，AFSA在国内外得到了广泛的使用，现在已经成为了一个非常活跃的研究方向。Jiang J.[10]等人提出基于粒子群优化算法（PSO）和人工鱼群算法（AFSA）的混合算法，结合了PSO和AFSA的优点，该算法增加了种群的多样性，提高了解的精度。KUMAR K.P.[11]等人提出了一种基于随机搜索算法的人工鱼群算法，通过在微电网方案中验证了算法的有效性，解决了现有可再生能源发电的最优调度问题。王培建[12]等对数控加工过程中，以最小单位切削能为目标，采用AFSA对其进行求解，发现能耗能够减少12.7%左右。蔡芸[13]等将人工鱼群算法应用于孔群加工路径优化的研究，建立以最短加工路径为目标的路径优化数学模型，获得的最优路径可以节省71.47%的行走路程。GAO Y.[14]等人提出了一种采用优化的人工鱼群算法对船舶导航系统的惯性测量装置的参数进行标定，模拟导航实验结果表明，所提出的标定方法能够满足船用陀螺罗经的校正精度和可靠性要求。

许多学者对于人工鱼群算法的优化性能和具体应用做了一定的研究，但是把AFSA用于混凝土锯切力的预测却鲜有报道。本文采用AFSA对混凝土锯切力进行建模，通过将预测锯切力与实验锯切力进行比较，发现AFSA能够根据给定的参数较为准确地预测混凝土锯切力，且预测精度比基于多元回归法的锯切力预测模型更高。因此，利用AFSA建立混凝土锯切力预测模型，可优化锯切参数，延长金刚石锯片的使用寿命，为金刚石锯片锯切混凝土的加工监控提供理论依据。

1　混凝土锯切实验

1.1　实验条件

本实验采用大连机床集团公司的VDL-600A立式加工中心进行混凝土锯切实验；工件为广西南宁嘉泰水泥制品有限公司制备的混凝土，成分和性能严格遵照国家标准《混凝土结构设计规范》，混凝土类型为C25，混凝土试件规格为150 mm×150 mm×150 mm，抗压强度为34.7 MPa；实验使用石家庄海川工具有限公司研制的金刚石圆锯片，规格为150 mm×22.2 mm×2.2 mm；Kistler9257B切削力测量系统用于锯切混凝土的锯切力采集。

1.2　实验方案

为验证混凝土锯切力预测模型的准确性，本实验以切削速度、切深和进给速度为变量，选用三因素三水平正交表。切削速度取12 m/s、18 m/s和24 m/s；切深取10 mm、15 mm和22 mm；进给速度取100 mm/min、200 mm/min 和 300 mm/min.实验过程中金刚石锯片受到x方向的锯切力最大，因此只对x方向的锯切力进行分析和建模。实验得到的锯切力原始信号如图1所示，整个锯切过程可以分为3个阶段：进刀阶段、平稳阶段和退刀阶段；锯片刚接触混凝土时，短期内锯切力急剧增大，达到一定值以后锯切力波动较小，此时锯片处于稳定锯切位置，离开工件时锯切力又急剧减少。对于锯切力信号，只考虑平稳锯切位置的信号，在锯切混凝土的实验中，每组实验重复6次，并取x方向的锯切力最大值的平均值。混凝土实验参数与测试结果如表1所示。

图1　混凝土锯切力原始信号图

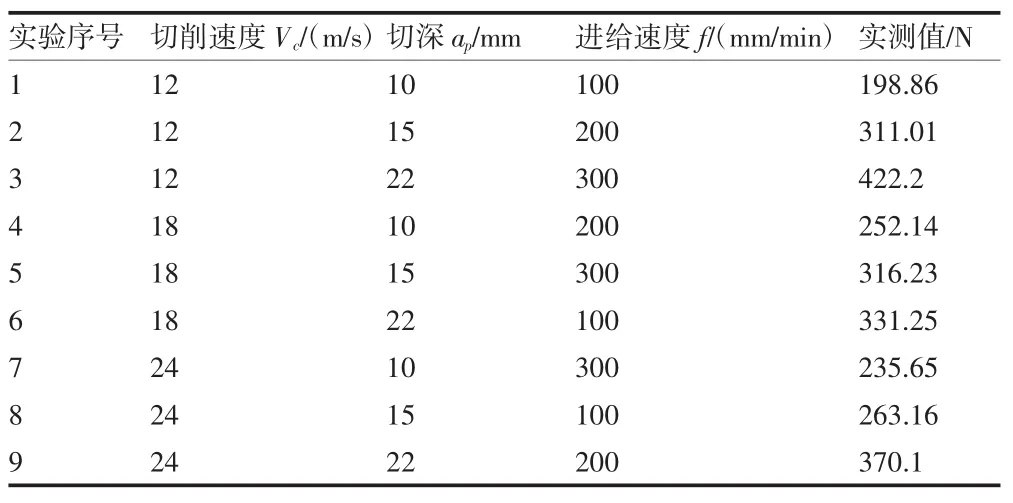
表1　混凝土实验参数与测试结果

2　混凝土锯切力预测模型建模

2.1　人工鱼群算法预测模型

2.1.1算法简介

人工鱼群算法是一种基于鱼群行为的群体智能优化算法，它模仿鱼群的觅食行为，在一片水域中，营养浓度最高的地方所含鱼的数目也是最多的。每条鱼寻找食物基于自己的行为方式，比如随机、觅食、聚群、追尾行为，而这些活动与求解函数的极值问题相似[11]。

人工鱼的行为描述：

（1）随机行为：在人工鱼Xa的视觉范围内随机的选择一个位置Xb，然后往这个方向移动一步。公式表述如下：

其中Xnest为人工鱼的下一个位置；rand（）表示（0，1）之间的随机数；visual为视觉范围。

（2）觅食行为：当前人工鱼的位置为Xa，在它视野范围内随机地选取另外一个位置Xb，比较两处的营养浓度Ya和Yb，当Yb＞Ya，说明此处食物浓度大，这条人工鱼往Xb方向进行移动，觅食行为可表示为式（2）：

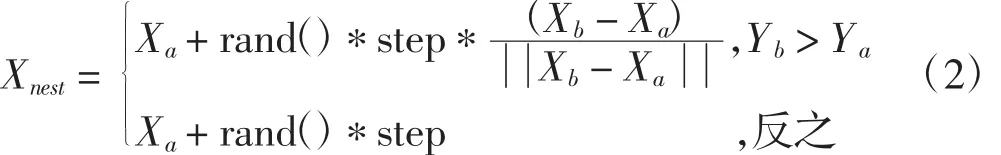
式中Y＝f（X）

（3）聚群行为：当前人工鱼的位置为Xa，探索其视觉范围内的人工鱼数目为nf，这nf条人工鱼的中心位置 Xc.若 Yc/nf＞ δ*Ya，说明 Xc处营养浓度较高而且鱼群密度稀疏，则按式（3）往Xc方向进行移动：

式中δ为鱼群的拥挤度因子

（4）追尾行为：当前人工鱼的位置为Xa，Xmost为当前视觉范围内食物浓度最高的人工鱼，若Ymost/nf＞δ*Ya，说明Xmost处营养浓度较高而且鱼群密度稀疏，则按照式（4）往Xmost方向进行移动：

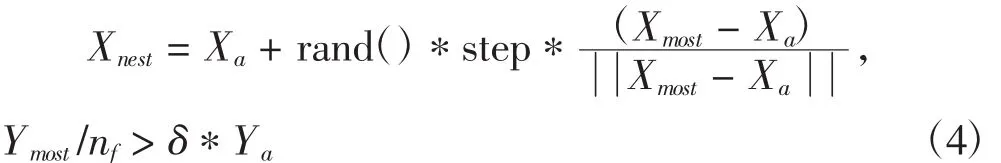
2.1.2数学模型的建立

根据传统的经验公式，以切削速度Vc、切削深度ap和进给速度f为变量得到锯切力Fx的公式为：

式中，x1为公式系数，x2、x3、x4为表示各因素对锯切力影响程度指数；以下应用人工鱼群算法和第1部分的实验数据进行求解。过程如下：

（1）目标函数建立。以实验锯切力Yk和预测锯切力 相对误差的绝对值之和作为食物浓度函数，对食物浓度函数△Y求取最小值：

（2）算法描述。首先随机初始化人工鱼的位置，计算每条鱼所在位置的食物浓度，取食物浓度最小者进入公告牌。（a）比较人工鱼执行追尾行为、聚群行为和觅食行为后食物浓度，选择执行食物浓度较小的行为，缺省状态则执行随机行为；（b）计算人工鱼检验自身位置的食物浓度，并与公告牌进行对比，如果优于公告牌，把相对应的位置写入公告牌，反之公告牌的值保持不变；（c）各鱼都执行（a）和（b）两个步骤，记为一次迭代。判断是否到达预设的迭代次数，若是，最终可在公告牌中得到最小食物浓度的人工鱼位置即锯切力公式中的4个未知系数。总的来说，人工鱼群算法充分利用了同伴的信息和外界的环境来调整下一步的搜索方向，通过不断改变自身的位置迭代更新鱼群的信息从而求解出最优值。

设定人工鱼条数为50条，迭代次数为50次，视觉范围为1，拥挤度因子为0.618，步长为0.1，迭代次数为200次，使用MATLAB进行仿真，结果如图2所示。

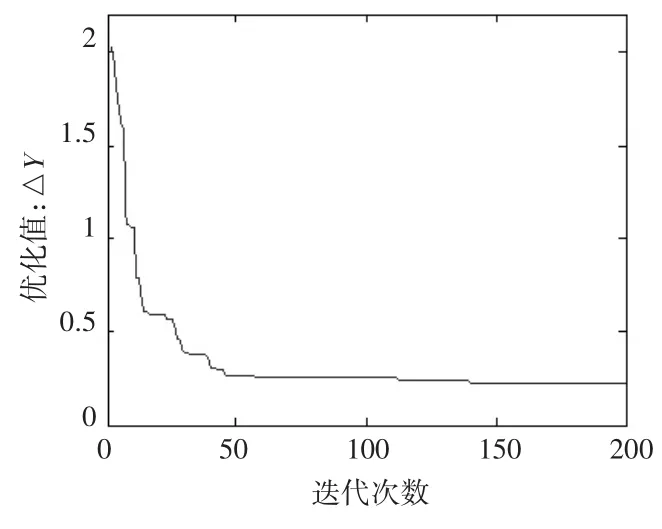
图2　实验锯切力和预测锯切力相对误差的绝对值之和函数迭代曲线

从图2迭代曲线可以发现，迭代次数在150左右函数基本收敛，通过人工鱼群算法对目标函数优化计算，最终得到FxAFSA的系数为x1=30.375 7，x2=-0.097 2，x3=0.632 7，x4=0.160 8，把系数代入到公式里面可得以下锯切力FxAFSA方程：

式中：FxAFSA为人工鱼群算法预测锯切力。

2.2　多元回归预测模型

通过对实验数据进行回归分析，建立混凝土锯切力回归预测模型。对经验公式（5）两边取对数有：

可得多元回归方程：

式中：Y=lnFx，b0=lnx1，X1=lnVc，X2=lnap，X3=lnf.应用多元线性回归法对式（9）进行回归分析，并根据表1的实验数据可以求得切削参数的各系数，利用matlab反求出式（5），从而得到锯切力的回归模型，建立如下锯切力Fx回的公式：

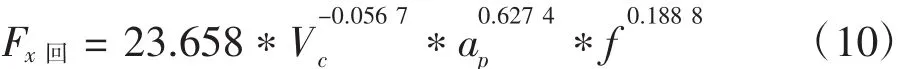
式中：Fx回为多元回归算法预测锯切力

对锯切力公式（10）进行显著性检验可得：r2=0.971 3，F=56.349 2，P=0.000 3 ＜ 0.05，可知回归模型成立。

3　人工鱼群算法和多元回归法锯切力预测结果对比

混凝土实验Fx锯切力和预测锯切力结果如表2和图3所示，从图3可以看出，两种方法的混凝土锯切力预测值和实验值都有较高的一致性；从表2可以看出通过人工鱼群算法预测，除了1号和4号，其它锯切力预测值的相对误差都很小，通过计算可知平均相对误差只有2.58%；采用多元线性回归预测模型对锯切力进行求解，可以得到其平均相对误差为2.86%.说明采用AFSA求解比多元线性回归求解的精确度更高，可以实现对混凝土锯切力的准确预测。从锯切力方程（7）和（10）可以发现对锯切力影响最大的因素为锯切深度，其次为进给速度，影响最小的是锯片切削速度。

表2　人工鱼群算法和多元回归法预测力与实测力对比

图3　不同参数下实验锯切力与预测锯切力对比图

4　结束语

本文通过人工鱼群算法建立了混凝土锯切力预测模型，发现预测锯切力与实验锯切力相吻合，平均相对误差只有2.58%，高于回归分析法建立的混凝土锯切力预测模型。证明了所建立预测模型的准确性；人工鱼群算法的预测精度比多元回归法更高；从锯切力方程可以发现对锯切力影响最大的因素为锯切深度，其次为进给速度，影响最小的是锯片转速；使用AFSA建立的混凝土锯切力预测模型能够达到较好的拟合效果。利用混凝土锯切力预测模型，可优化锯切参数，延长金刚石锯片的使用寿命，为金刚石锯片锯切混凝土的加工监控提供理论依据。

参考文献：

[1]胡映宁，许振力，胡珊珊，等.基于声发射技术金刚石组合圆锯片干切混凝土的切削状态研究[J].金刚石与磨料磨具工程，2008，166（04）：28-34.

[2]郑春英.花岗石高效锯切加工技术实验研究[D].济南：山东大学，2010.

[3]LI Y，YU Y，XU X.Analysis of Cutting Forces in the Deep Sawing of Granite with a Diamond Saw-blade（Superabrasive/new wheel grinding process）[J].The Japan Society of Mechan ical Engineers，2017：205-208.

[4]ZHANG Z M，XIAO H W，WANG G Z，et al.Modeling and Experimental Study on Cutting Force of Diamond Circular Saw in Cutting Granite Using Response Surface Methodology[J].Advanced Materials Research，2013：2191-2195.

[5]KARAKURT I.Application of Taguchi method for cutting force optimization in rock sawing by circular diamond saw blades[J].SADHANA-ACADEMY PROCEEDINGS IN ENGI NEERING SCIENCES，2014，39（5）：1055-1070.

[6]陈亚洲，刘晓刚，叶崇化，等.金刚石锯切优化技术[J].石材，2016（09）：10-11.

[7]郑冬锐，胡珊珊，王成勇，等.金刚石圆锯片干切素混凝土切削动态特征的多尺度分析[J].金刚石与磨料磨具工程，2015（03）：40-45.

[8]汪 靖.群体智能优化算法及其在GPU上的并行化研究[M].南昌：江西高校出版社，2014：4-5.

[9]李晓磊，邵之江，钱积新.一种基于动物自治体的寻优模式：鱼群算法[J].系统工程理论与实践，2002（11）：32-38.

[10]JIANG J，BO Y，SONG C，et al.Hybrid Algorithm Based on Particle Swarm Optimization and Artificial Fish Swarm Al gorithm[M].Advances in Neural Networks-ISNN 2012.Springer Berlin Heidelberg，2012：607-614.

[11]KUMAR K P，SARAVANAN B，SWARUP K S.Optimiza tion of Renewable Energy Sources in a Microgrid Using Artifi cial Fish Swarm Algorithm[J].Energy Procedia，2016（90）：107-113.

[12]王培建，刘 强，王 健，等.一种面向绿色高效的数控铣削参数优化方法[J].航空制造技术，2016（07）：50-54.

[13]蔡 芸，周立炜.人工鱼群算法在孔群加工路径优化中的应用研究[J].武汉科技大学学报，2011（03）：182-185.

[14]GAO Y，GUAN L，WANG T.Optimal artificial fish swarm algorithm for the field calibration onmarine navigation[J].Measurement，2014（50）：297-304.