RN上的分数p-Laplacian方程弱解的存在性*
2018-04-02程伟柏仕坤徐家发
程伟,柏仕坤,徐家发
(重庆师范大学数学科学学院,重庆401331)
本文主要研究以下RN上的分数p-Laplacian方程弱解的存在性:
(1)
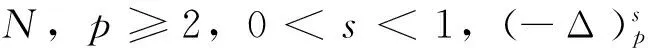
x∈RN
为了获得问题(1)弱解的存在性,我们首先给出本文所使用的分数Sobolev空间Ws,p(RN) 的相关知识,详见文献[1]。
定义Gagliardo半范数如下:
其中u:RN→R是一可测函数。定义分数Sobolev空间
Ws,p(RN){u∈Lp(RN):u是可测的, 且[u]s,p<∞}
鉴于势函数V(x)的出现,考虑如下的子空间:
Xs
并在其上赋予范数
在以下的行文中仅采用范数‖·‖Xs,并简记为‖·‖。
本文中,势函数V(x)满足条件:

1 若干引理与定义

由连续嵌入可得存在τq>0使得

(2)
近年来分数阶Laplacian方程是研究的热点问题,有大量的文献讨论该类方程解的存在性等问题,参见文献[2-9]及其所附参考文献。在文献[3]中,作者采用山路定理,在经典的Ambrosetti-Rabinowitz条件下,获得了分数阶薛定谔方程非平凡弱解的存在性:
(-Δ)su+V(x)u=f(x,u),x∈RN
在文献[4]中,作者采用变化的喷泉定理,在非线性项次临界增长的情况下,获得了文献[3]中问题无穷多能量解的存在性。受以上文献的启发,本文采用山路定理来研究问题(1)非平凡弱解的存在性。为此,本文始终假设非线性项f满足次临界条件:
(H1) 存在d1>0,d2>0使得
|f(x,t)|≤d1|t|p-1+d2|t|q-1,
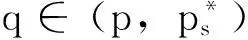
以下给出问题(1)对应的能量泛函J:Xs→R如下:
(3)


从而由条件(H1)可得


d1|t|p+d2|t|q,∀(x,t)∈RN×R
(4)
结合引理1可知J,ψ都是良定义的,且有如下的引理。
引理2若条件(V)和(H1)成立,则泛函J∈C1(Xs,R),且对任意的v∈Xs,其导数为
(u(x)-u(y))(v(x)-v(y))dxdy+
(5)
并由此可知J的临界点就是问题(1)的弱解。
证明记(Xs)*是Xs的对偶空间,定义算子A:Xs→(Xs)*如下:
〈Au,v〉=
下证A是有界连续算子。事实上,对任意的u,v∈Xs,根据Hölder不等式,有
(u(x)-u(y))(v(x)-v(y))dxdy≤
‖u‖p-1‖v‖
和
‖u‖p-1‖v‖
从而A有界。再证A的连续性。为此需要如下的不等式:
||a|p-2a-|b|p-2b|≤2p-2(p-1)|a-b|·
(|a|+|b|)p-2,∀a,b∈R
令{un}⊂Xs,u∈Xs使得un→u。对任意的v∈Xs,‖v‖≤1,由Hölder不等式可得
c2‖un-u‖(‖un‖p-2+‖u‖p-2)→0,n→∞
和
(un(x)-un(y))-|u(x)-u(y)|p-2·
(u(x)-u(y))||v(x)-v(y)|dxdy≤
(un(x)-un(y))-|u(x)-u(y)|p-2·
c4‖un-u‖(‖un‖p-2+‖u‖p-2)→0,
n→∞
其中ci(i=1,2,3,4)为正常数。
综上可得
从而A是连续的。
接下来首先证明
∀u,v∈Xs
由条件(H1), 结合(2)式可得
∀u,v∈Xs
(6)
从而根据中值定理和Lebesgue控制收敛定理,对任意的∀u,v∈Xs和s∈[0,1],有
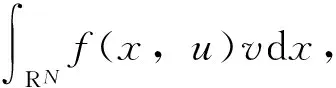
再由(6)式可知ψ′(u)关于v是线性有界的,则ψ′(u)∈(Xs)*。
下证ψ′:Xs→(Xs)*是弱连续的。假设
un→u弱收敛于Xs
(7)
则由引理1可知

(8)
un(x)→u(x),a.e.x∈RN
(9)
注意到,
‖ψ′(un)-ψ′(u)‖(Xs)*=

从而存在v0∈Xs,‖v0‖=1使得
对r=p,q由于un→u强收敛于Lr(RN)中,根据文献[10]中的引理A.1,存在{un}的子序列,仍记为{un},以及g1∈Lp(RN),g2∈Lq(RN),使得对几乎所有的x∈RN,有
|un(x)|,|u(x)|≤gi(x),i=1,2,∀n∈N
从而根据条件(H1)和Young不等式,可推出
|f(x,un)-f(x,u)||v0|≤
d1(|un|p-1+|u|p-1)|v0|+
d2(|un|q-1+|u|q-1)|v0|≤
2d1|g1|p-1|v0|+2d2|g2|q-1|v0|≤
从而根据Lebesgue控制收敛定理,注意到(9)式,有
这显然是矛盾的。从而l=0,因此
‖ψ′(un)-ψ′(u)‖(Xs)*→0,n→∞
类似可证ψ′是连续的。
综上所述,J∈C1(Xs,R),并且易知J的临界点就是问题(1)的弱解。证毕。
定义1[10-11]设(X,‖·‖)是实Banach空间,J∈C1(X,R) 。称J满足(Cc)条件,如果对于X中的任意序列{un}满足:
J(un)→c,‖J′(un)‖(1+‖un‖)→0,
(n→∞)
则序列{un}均有收敛子列。
引理3[10-11](山路定理) 设(X,‖·‖)是实Banach空间,J∈C1(X,R)满足(Cc)条件以及
(i)J(0)=0且存在β>0,ρ>0使得J(u)≥β,∀u∈X,‖u‖=ρ;
(ii) 存在e∈X,‖e‖>ρ,使得J(e)≤0。

2 主要结果
首先给出本文所使用的假设条件:

(H3) 存在β*∈L1(RN)使得
σ(x,t)≤σ(x,s)+β*(x),∀0≤t≤s或者s≤t≤0
其中σ(x,t)=f(x,t)t-pF(x,t);
(H4)f(x,t)=o(|t|p-2t),t→0,对x∈RN一致成立。
注1条件(H3)是验证(Cc)序列有界的重要条件,被广泛运用到各类文献[7,12-14]。在文献[12]中,作者利用(H3)等条件获得了如下问题非负、非平凡弱解的存在性:
-Δpu-Δqu+a(x)|u|p-2u+
b(x)|u|q-2u=f(x,u),
x∈RN
例如,令F(x,t)=|t|pln(|t|+1),则它满足条件(H3), 却不满足Ambrosetti-Rabinowitz条件:存在μ>p使得
0<μF(x,t)≤f(x,t)t,∀(x,t)∈RN×R{0}
引理4若条件(V), (H1)-(H3)成立,则泛函J满足(Cc)条件。
证明令{un}⊂Xs是一(Cc)序列,即对任意
c>0,J(un)→c,‖J′(un)‖(1+‖un‖)→0,n→∞
这表明
c=J(un)+o(1),〈J′(un),un〉=o(1),n→∞
从而
(10)
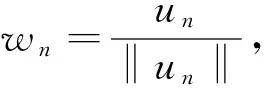
wn→w弱收敛于Xs
(11)

(12)
以下分两种情况讨论。
情况I:w不恒等于0。
记集合Ω≠={x∈RN:w(x)≠0}。显然Ω≠有正的Lebesgue测度,且|un(x)|→∞,∀x∈Ω≠。因而在Ω≠中,由条件(H2)可得
从而根据Fatou引理,有
然而根据(10)式可知
这两式显然是矛盾的。
情况II:w恒等于0。

下证J(tnun)有界。若tn=0,J(0)=0;若tn=1,J(tnun)=J(un)→c,这也是有界的。仅考虑tn∈(0,1),对足够大的n, 有
运用条件(H3)可得
其中c5是一正常数。

故对足够大的n,有
这又是矛盾。
综合上述两种情况可知{un}在Xs中是有界的。从而存在u∈Xs使得在子列意义下,(7)-(9)式成立。下证un→u强收敛于Xs。
注意到
〈J′(un)-J′(u),un-u〉=
〈Aun-Au,un-u〉-〈ψ′(un)-
ψ′(u),un-u〉→0
先证
〈ψ′(un)-ψ′(u),un-u〉→0
(13)
事实上,根据条件(H1), (2) 式, (8)式可得
d2(|un|q-1+|u|q-1)]
|un-u|dx≤
再结合ψ′的定义,可知(13)式成立。
由(13)式可知
〈Aun-Au,un-u〉→0
(14)
注意到在Lp(RN)中un→u,根据Hölder不等式,有
(‖[V(x)]1/pun‖p-‖[V(x)]1/pu‖p)≤
从而
‖[V(x)]1/pun‖p→‖[V(x)]1/pu‖p
(15)
另一方面注意到,对任意的u,v∈Xs,有
(u(x)-u(y))-|w(x)-w(y)|p-2·
(w(x)-w(y))][(u(x)-u(y))-
(w(x)-w(y))]dxdy=
[(u(x)-u(y))-(w(x)-w(y))]dxdy-
(w(x)-w(y))(u(x)-u(y))dxdy+
结合(14)-(15)式可知[un]s,p→[u]s,p,再由(15)式可知‖un‖→‖u‖。因为Xs是局部一致凸空间,
弱收敛+依范数收敛⟹强收敛
所以un→u强收敛于Xs。证毕。
定理1若条件(V), (H1)-(H4)成立,则问题(1)至少存在一个非平凡弱解。
证明由引理4知仅需再证引理3中条件(i), (ii)成立。根据条件(H1), (H4)可得对任意的ε>0,总存在cε>0使得
|F(x,t)|≤ε|t|p+cε|t|q,∀(x,t)∈RN×R
结合(2)式可得
进而引理3(i)成立。
另一方面,由条件(H1), (H2)知,存在足够大的M>0使得

注意到,若M足够大,J(τv0)→-∞,τ→+∞。由此可知存在
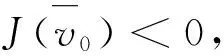
参考文献:
[1]NEZZA D I E, PALATUCCI G, VALDINOCI E. Hitchhiker’s guide to the fractional Sobolev spaces [J]. Bull Sci Math, 2012, 136(5):521-573.
[2]TORRES C. On superlinear fractionalp-Laplacian in Rn[J].Mathematics, 2014.
[3]SECCHI S.Ground state solutions for nonlinear fractional Schrödinger equations in RN[J].J Math Phys, 2012, 54(3): 056108-305.
[4]TENG K. Multiple solutions for a class of fractional Schrödinger equations in RN[J].Nonlinear Analysis: Real World Applications, 2015, 21: 76-86.
[5]GUO T X, SUN H R. Solutions of nonlinear Schrödinger equation with fractional Laplacian without the Ambrosetti-Rabinowitz condition [J]. Applied Mathematics and Computation, 2015, 257(C): 409-416.
[6]XU J, WEI Z, DONG W.Existence of weak solutions for a fractional Schrödinger equation [J]. Commun Nonlinear Sci Numer Simulat, 2015, 22 (1/2/3): 1215-1222.
[7] DONG W, XU J, WEI Z. Infinitely many weak solutions for a fractional Schrödinger equation [J]. Boundary Value Problems, 2014, 2014(1): 159.
[8]赵继红,冯兆永. 具有临界增长边界条件的p-Laplace方程解的存在性[J]. 中山大学学报(自然科学版), 2010, 49 (1): 1-4.
ZHAO J H, FENG Z Y.Existence of weak solutions for thep-Laplace equation with critical growth in boundary conditions [J].Acta Scientiarum Naturalium Universitatis Sunyatseni, 2010, 49 (1): 1-4.
[9]崔德标. 二阶非自治(q,p) -Laplace 方程组解的存在性[J]. 中山大学学报(自然科学版), 2013, 52 (3): 45-48.
CUI D B. Existence of solution of second-order nonautonomous equations with (q,p) -Laplace [J].Acta Scientiarum Naturalium Universitatis Sunyatseni, 2013, 52 (3): 45-48.
[10]WILLEM M. Minimax theorems [M]. Boston: Birkhäuser, 1996.
[12]CHAVES M F, ERCOLE G, MIYAGAKI O H. Existence of a nontrivial solution for the (p,q)-Laplacian in RN without the Ambrosetti-Rabinowitz condition [J]. Nonlinear Anal: Theory, Methods & Applications, 2015, 114: 133-141.
[13]MIYAGAKI O H, SOUTO M A S. Superlinear problems without Ambrosetti and Rabinowitz growth condition [J]. J Differential Equations, 2008, 245(12): 3628-3638.
[14]CHUNG N T, TOAN H Q. On a class of anisotropic elliptic equations without Ambrosetti-Rabinowitz type conditions [J]. Nonlinear Analysis: Real World Applications, 2014, 16(16): 132-145.
