无人机的动力学方程式和编队控制

于晓敏

（四川大学计算机学院，成都 610065）

0　引言

随着计算机技术、传感器技术、通信技术的飞速发展，动态三维环境中的多飞行器系统研究已经得到了极大的发展。因为编队的队形控制广泛地应用于搜索营救任务、运输、生化物品定位、作战任务等领域中，所以编队队形控制一直是研究热点之一。本文将人工势场与旋转矢量结合来控制无人机编队。编队中指定一个无人机为领队无人机，其他队员无人机跟随领队无人机共同追踪一个移动目标。

1　无人机动力方程

首先，我们考虑无人机的动力学方程已被广泛地应用于许多文献。无人机的动力学方程式可以用自由度质量模型描述如下：

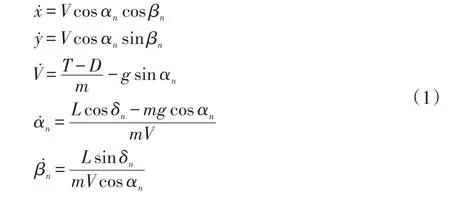
无人机控制输入是发动机的推力T、升力L，和倾斜角δ。高度非线性的无人机模型可以利用反馈线性化为线性，如下所示：

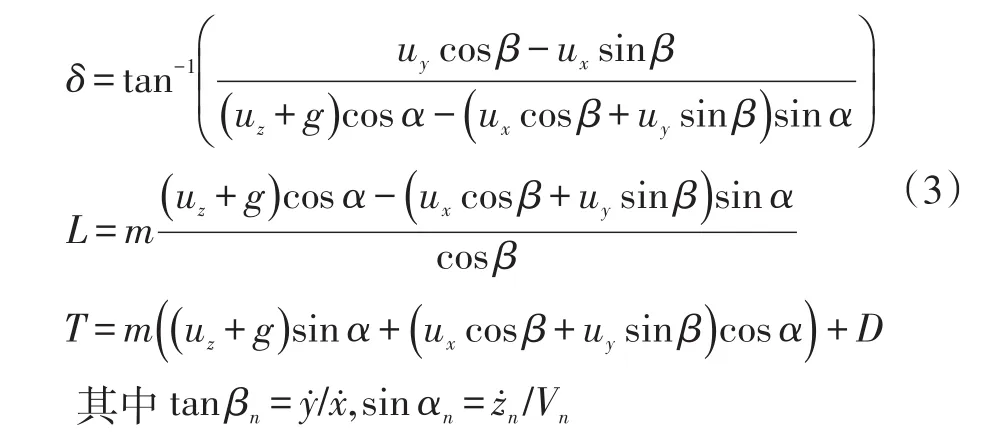
2　无人机编队控制

在这一部分，提出了一种扩展的人工势场法，用于三维环境下无障碍飞行的无人机编队跟随。先设计无人机成员控制算法。

成员无人机的运动受人工力的影响，主要由如下两部分组成：

其中m是第n个无人机的质量，fnc是控制无人机到达中心无人机的球面的吸引力，fnc可以描述为：

其中

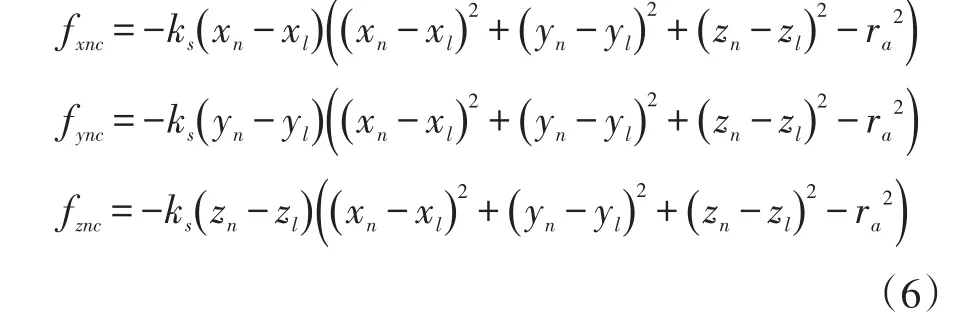
其中(xl,yl,zl)是领队无人机的坐标。ks是增益系数。

Fn是无人机的斥力合力，使无人机均匀分布在球面上。以领队无人机坐标(xl,yl,zl)为中心，所有无人机都带有正电荷或者负电荷。斥力对具有相同电荷量的无人机产生影响。无人机在球面上定义的控制力，其半径是ra，中心是()xl,yl,zl。当无人机在球面上相切时产生的斥力的合力为零时，无人机达到平衡点。这意味着无人机之间的距离是相等的。然后，目标就实现了。两个无人机之间的斥力定义如下：

其中qn第n无人飞行器的带电量，qi是第i无人飞行器的电量，kr是互斥常系数（感觉像是库伦常数），rni是第n无人机与第i无人机之间的距离。无人机总数为N。因此，第n无人机上的其他无人机的排斥力的结果如下所示：

如图1所示，P是无人机的初始位置。P'是移动后无人机的位置。Q1是P在X0-O-Y0平面投影。Q2是 P′在 X0-O-Y0平面投影。Q3是P′在Z0-O-Q1平面投影。将合力在三个方向上分解，分力分别在x轴方向、y轴方向和z轴方向上。图1所示如下：

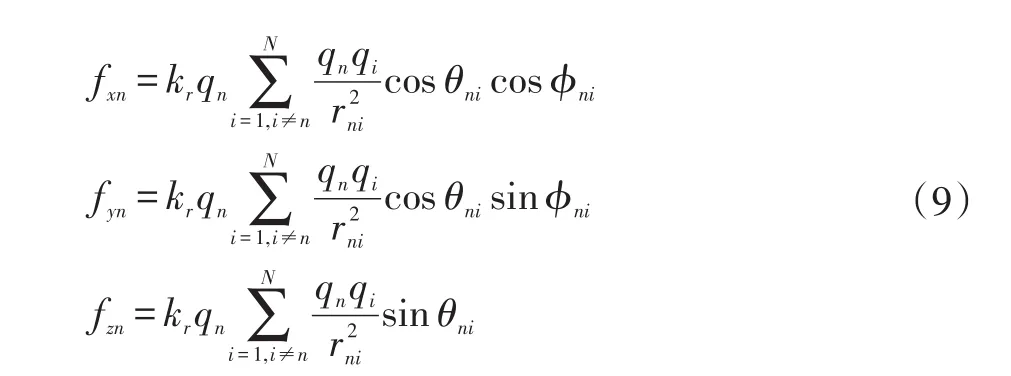
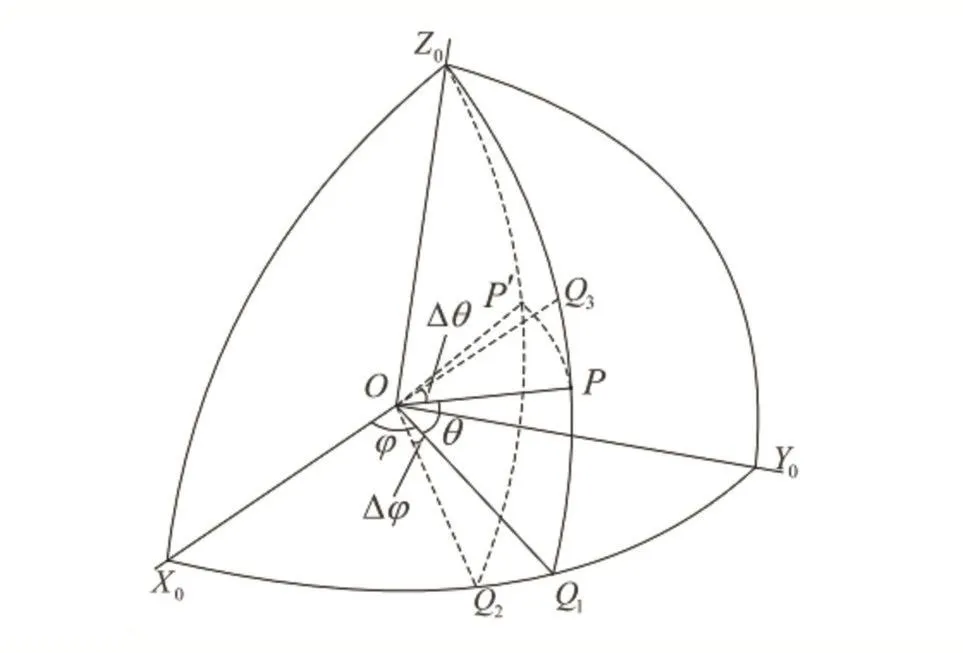
图1　无人机运动方向

其中：

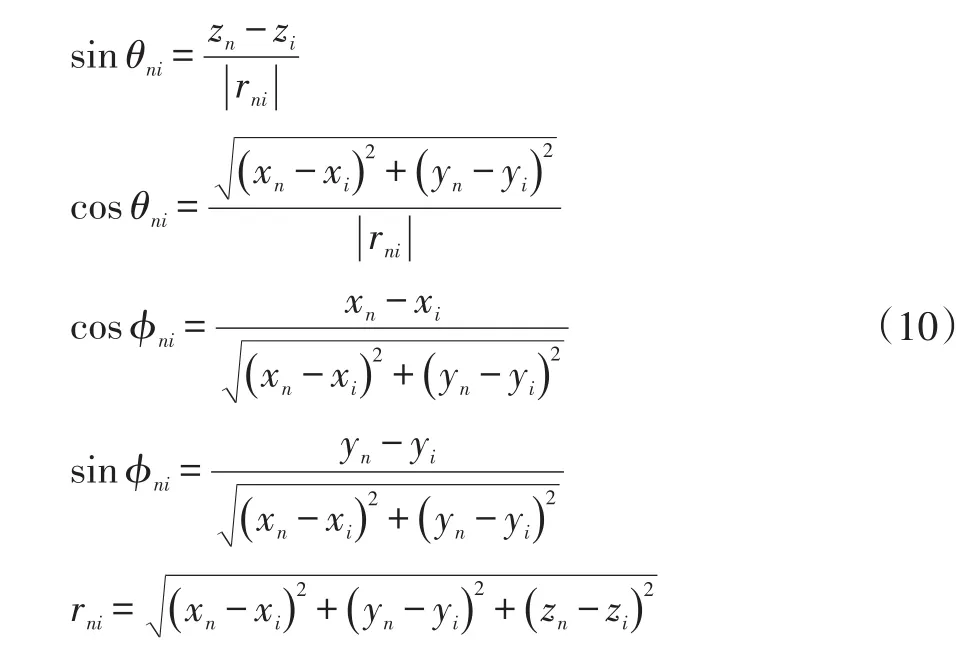
考虑第n无人机的动力学方程（2），基于虚拟结构的第n无人机动力学方程可以改写为：

综上所述，斥力与避免无人驾驶车辆碰撞成1 rni的比例。控制力(uxn,uyn，uzn)在将无人机引导到球面上的平衡点。

3　结语

本文提出了一种基于人工势场法结合旋转矢量的多无人机系统跟踪无人机驾驶员运动目标的编队控制方法，为以后研究无人机避障做了很好的铺垫。

参考文献：

[1]陈晓飞.无人机系统建模仿真研究及应用.学位论文.南昌航空大学，2014

[2]易姝姝.无人机飞行场景及数据的可视化仿真与实现.学位论文.电子科技大学，2010