考虑降雨类型的基岩型浅层边坡稳定性分析方法

李绍红，朱建东，王少阳，吴礼舟

(成都理工大学地质灾害防治与地质环境保护国家重点实验室，四川 成都 610059)

大量研究和工程案例表明，降雨是滑坡尤其是浅层滑坡的主要致灾因子[1～6]。降雨诱发的浅层滑坡滑面多为基岩面或平行于基岩面，而这种平行于基岩面的潜在滑面又被称之为湿润锋。基岩型浅层边坡是指坡体上部为土层、底部为不透水的基岩层的一类边坡[7]，降雨对该类边坡稳定性影响显著，故其在降雨作用下的稳定性一直是滑坡领域的研究热点[8～10]。

利用降雨入渗模型研究基岩型浅层边坡稳定性是一种实用且有效的途径。常见的降雨入渗模型包括Green-Ampt入渗模型、Philip模型、Horton入渗模型等[11]。其中Green-Ampt入渗模型由于具有原理简单、参数较少的优点，在实际工程尤其是在浅层边坡稳定性分析中得到了广泛运用。Green-Ampt入渗模型最初是用于解决水平地表的入渗问题，由于实际边坡都具有一定的倾角，Chen等[12]在原始Green-Ampt入渗模型中引入了倾角变量，提出适用于研究滑坡问题的改进Green-Ampt入渗模型。此后，许多学者尝试用Green-Ampt入渗模型及其改进形式研究浅层边坡稳定性，如马世国等[8]根据原始Green-Ampt入渗模型(即没有考虑倾角)和无限边坡模型研究了浅层边坡稳定性；张群等[9]采用经典Green-Ampt入渗模型结合室内试验分析了南江浅层滑坡的成因机制；汪丁健等[10]认为经典Green-Ampt入渗模型忽略了雨水入渗过程中在土体内部的渗流部分，建立了改进Green-Ampt入渗模型用于探讨浅层边坡稳定性。

虽然Green-Ampt入渗模型已在浅层边坡稳定性分析中得到了诸多应用，但这些计算大多是在等降雨强度下进行的，这显然不符合实际情况。Ng等[13]和罗渝等[14]将实际降雨情况划分为均匀性降雨、递增型降雨、递减降雨、峰值型降雨四种类型。罗渝等[14]还结合Rsoso坡地水文模型(降雨与地下水位关系的模型)和不同降雨特性对浅层边坡稳定性开展了研究。然而，坡地水文模型参数较多，实现较为复杂。在已有研究的基础上，本文将前人划分的降雨类型建立统一表达形式，并结合入渗理论对浅层滑坡的稳定性开展研究。以期能够为不同降雨类型下浅层滑坡的稳定性提供一种简单实用的分析方法。

1 多种降雨类型的统一表达形式

为减小降雨作用下边坡稳定性计算的难度，目前多数计算方法都将降雨强度视为不变量，即等雨强。事实上，实际降雨强度是降雨历时的因变量。Ng等[13]和罗渝等[14]总结了四种降雨类型：均匀型降雨(等雨强)、递增型降雨(降雨强度随历时的增大而增大)、递减型降雨(降雨强度随历时的增大而减小)、峰值型降雨(降雨强度先随历时的增大而增大，尔后随历时增大而减小)，相关示意图见图1。可认为，上述四种降雨类型皆为极端情形。在此笔者给出如上四种降雨的统一形式，见图2。

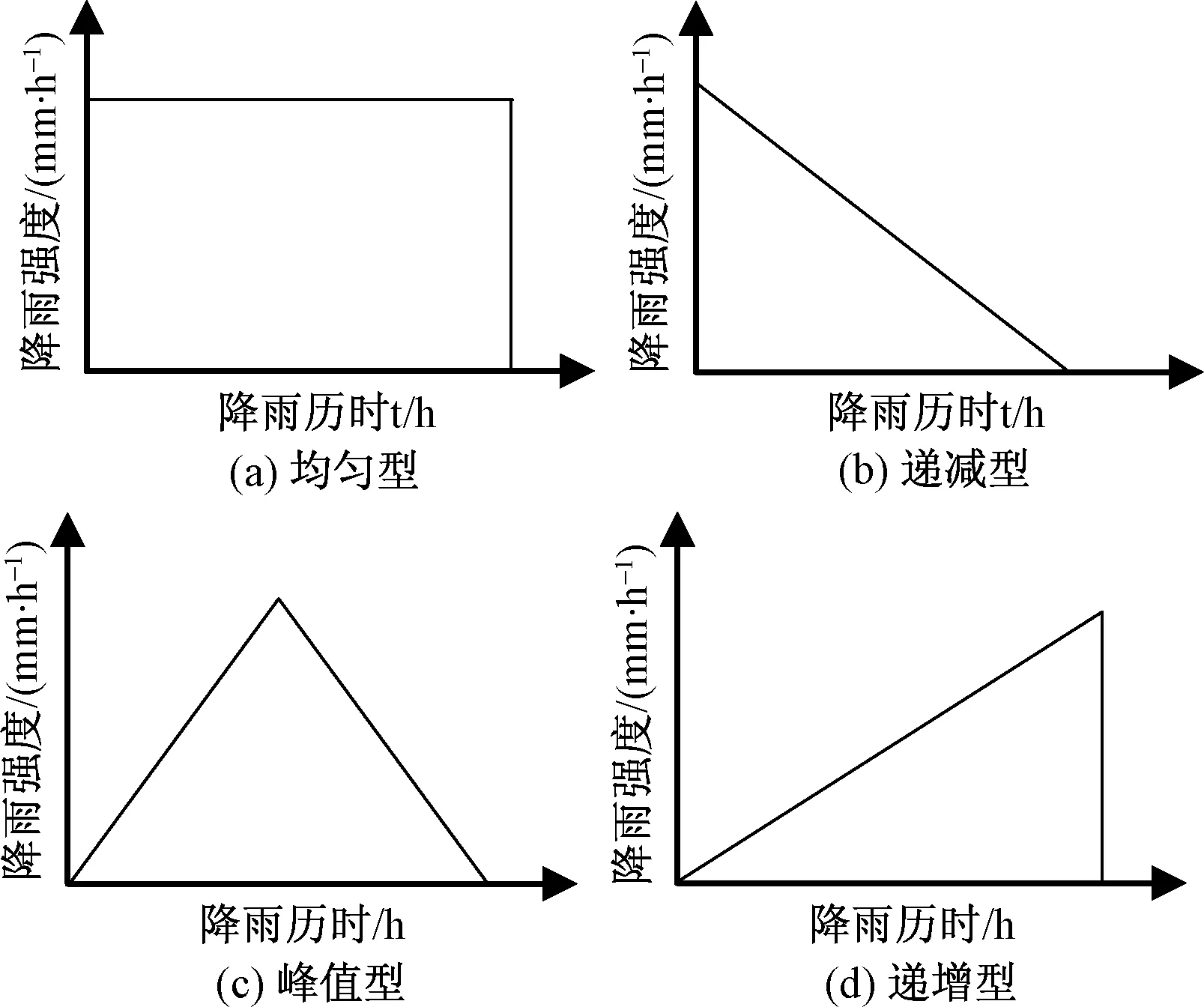
图1 四种不同降雨类型[14]Fig.1 Four different rainfall types[14]

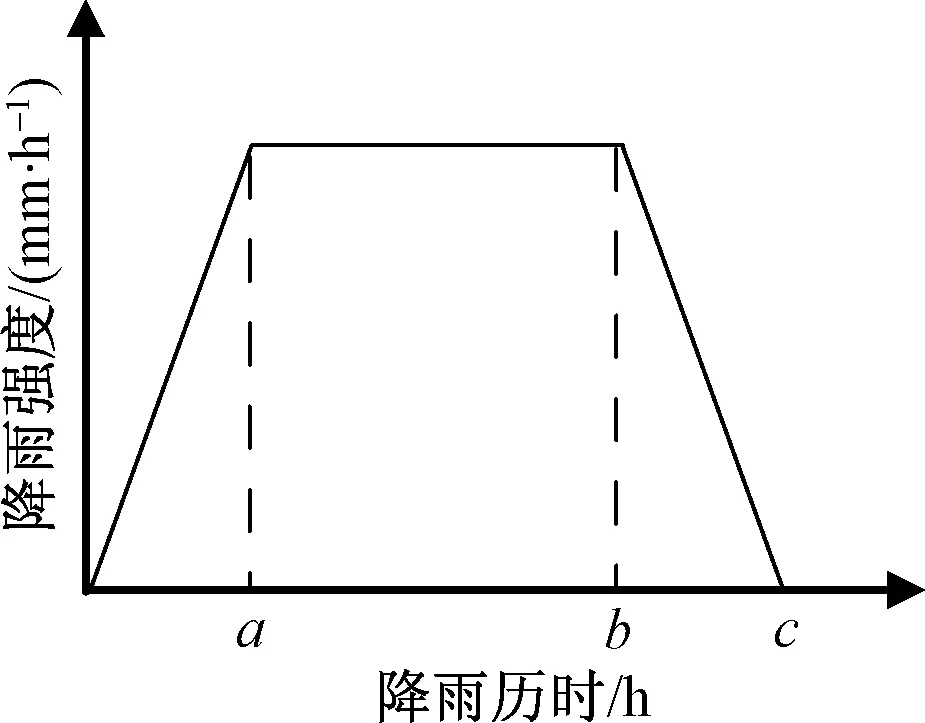
图2 常规型降雨Fig.2 Conventional rainfall type

根据图2，降雨强度q随降雨历时t的变化可表达为：

(1)

式中：qmax——最大降雨量；

a、b、c——表征降雨阶段的参数。

令a=b=0，则退化为递减型降雨；令c=b=a，则退化为递增型降雨；令a=b，则退化为峰值型降雨；令a=0和c=b，则退化为均匀型降雨。事实上，实际情形的降雨多是：雨强先随历时逐渐增大，其后一段时间等雨强，而后雨强逐渐减小，可认为：式(1)归纳的降雨强度历时规律更为合理。本文将式(1)归纳的降雨类型称之为常规型降雨。

2 基岩型浅层边坡稳定性分析方法

2.1 计算不同降雨历时下的湿润锋深度

根据基岩型浅层边坡的地质特征，即不透水基岩层上覆厚度较浅的第四系松散覆盖层，在降雨作用下，随着降雨的不断入渗，表层土体逐渐趋于饱和状态，水劣化作用降低了松散覆盖层土体的抗剪强度，进而影响边坡的整体稳定性。结合非饱和土力学和入渗理论，降雨下基岩型浅层边坡可概化为如图3所示的力学模型[15]。

图3 降雨入渗下的基岩型浅层边坡力学模型[15]Fig.3 Mechanical model of bedrock shallow slopes under rainfall infiltration[15]

通常而言，在降雨初期，雨水的入渗根据雨量决定，即土体处于流量控制边界。此时的入渗率：

i1=qcosα

(2)

式中：α——边坡坡角。

根据雨量平衡假设，有：

zf·Δθ=i1·t

(3)

式中：zf——湿润锋入渗深度；

t——降雨历时；

Δθ——湿润区湿润前后含水量差。

为简化计算，通常将式(2)中的q视为定值，即用等雨强替换变雨强[8～10]。现将q视为变量，其值由式(1)决定。由图1和式(2)，式(3)可表述为：

(4)

对式(3)进行分段积分，有：

(5)

随着雨水的渗入，入渗率由土体的渗透系数决定，即土体由流量控制边界转化为水头控制边界。由此决定的渗透率可根据达西定律按下式得出：

(6)

该阶段的入渗模型为：

(7)

式中：ks——饱和渗透系数；

Sf——湿润锋处基质吸力水头。

湿润锋下行深度变化由流量控制边界转为水头控制边界的条件为i1=i2。联立式(1)～(5)，可以获得两阶段的临界降雨历时和临界湿润锋深度，分别记为tp和zp。另一方面，对于递减型、峰值型和常规型降雨，其降雨量在后期存在一个衰减过程，在此过程中，由雨水控制的流量入渗边界计算得到的入渗率将再次小于水头控制决定的入渗率，当达到临界值后，入渗模式再次由水头入渗转为流量入渗，记此时的临界降雨历时和临界湿润锋深度分别为tp1和zp1。则在整个过程中的湿润锋深度的控制方程可写为：

(8)

2.2 根据无限边坡模型计算稳定性系数

对于基岩型浅层边坡，降雨入渗常常会引起沿平行于坡面的湿润锋或基岩面的顺层滑动破坏。鉴于此，常用无限边坡模型来计算该类边坡的稳定性系数，借助于图3的力学模型，潜在滑动面为湿润锋时的稳定性系数为：

(9)

潜在滑动面为基岩面时的稳定性系数为：

(10)

式中：Δγ——饱和重度γsat和初始重度γ0之差；

c、φ——有效黏聚力和有效内摩擦角；

ψ0——边坡土体的基质吸力；

φb——土体基质吸力内摩擦角；

h——基岩上覆土层厚度。

边坡整体稳定性系数f按最不利情况取值，即：

f=min{Fs,Fr}

(11)

根据已有研究表明[6～7]：通过联解式(9)～(10)，令Fr=Fs，可得到两者相等的临界深度，当湿润锋下行深度小于该临界深度时，基岩面处的稳定性系数较湿润锋处稳定性系数小，即f=Fr；当湿润锋深度较该临界深度大时，基岩面处的稳定性系数较湿润锋处稳定性系数大，即f=Fs。而若通过编制程序计算，则只需直接比较两种潜在滑动面稳定性系数大小即可，而无需进行此繁琐的计算(即判断f=Fs或f=Fr的成立条件)，本文在此直接按该方法计算。

在某些情况下，基岩上可能存在地下水，只需考虑水对土体容重的影响，按照类似的方法求解即可。

3 算例分析

假设某基岩型浅层边坡，不透水基岩层上覆2 m厚土层，基岩上不存在地下水，有关计算参数取值见表1，各参数意义见文中第2节。

表1 计算参数Table 1 Calculation parameters

应用本文所建立的数学模型，开展降雨对基岩型浅层边坡稳定性影响的计算。为体现降雨特性对边坡稳定性的影响，在设定降雨历时和降雨总量相同的情况下，分别设计了五种计算方案：方案一，取a=5 h,b=15 h,c=20 h,qmax=30 mm/h，该计算方案对应图2所示的降雨类型，即常规型降雨；方案二，取a=0 h,b=20 h,c=20 h,qmax=22.5 mm/h，计算方案对应均匀型降雨；方案三，取a=0 h,b=0 h,c=20 h,qmax=45 mm/h，对应递减型降雨；方案四，取a=20 h,b=20 h,c=20 h,qmax=45 mm/h，对应递增型降雨；方案五,取a=10 h,b=10 h,c=20 h, qmax=45 mm/h，对应峰值型降雨。

五种计算方案对应的湿润锋变化情况如图4(a)所示，可见：不同的降雨特性导致湿润锋下降速率不一致，且具有较为明显的时效性。如在降雨初期(<5 h，下同)，递减型降雨导致的湿润锋下降最为迅速，其次是常规型降雨和峰值型降雨，最后是均匀型降雨和递增型降雨，这和五种降雨类型的降雨强度-时间曲线较为一致；在降雨中期(5～15 h，下同)，各种降雨特性对湿润锋下降速率影响的波动较大，总体上递减型导致的湿润锋下降最为迅速；在降雨后期(>15 h，下同)，常规型、峰值型、均匀型和递增型导致的湿润锋下降速率加快，递减型后期的下降速率较中期减缓，这主要是由于降雨强度减小，入渗模式由水头控制变为流量控制所致。

五种计算方案对应的稳定性系数变化情况如图4(b)所示，可见：不同的降雨特性导致边坡稳定性系数下降速率也不一致，同样具有较为明显的时效性。在降雨初期，递减型降雨引起稳定性下降最快，其次是均匀型和常规型降雨，最后是峰值型降雨和递增型降雨。在降雨中后期，稳定性系数的变化和湿润锋变化是一致的，这可以由式(9)～(11)快速得到。对于降雨中期和后期，仍然可以得到与湿润锋变化类似的规律，在此不再累叙。

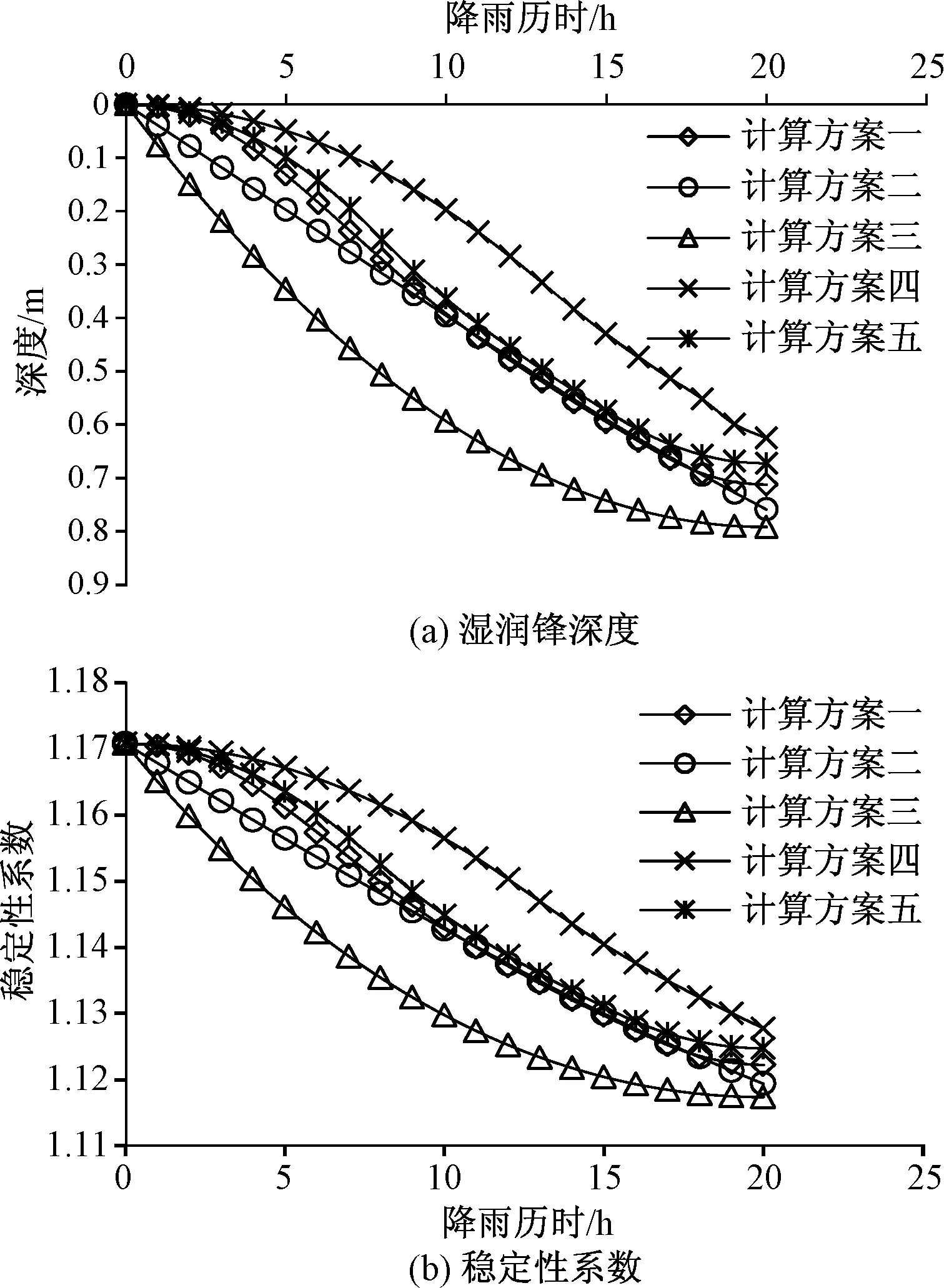
图4 湿润锋深度(a)及稳定性系数(b)计算结果Fig.4 Results of (a) wetting front depth and (b) stability coefficient

从以上的算例可以看出，即使是在相同降雨量和降雨历时下，不同降雨模式对边坡稳定性系数影响差异明显。从整体上看，均匀型降雨虽然和峰值型降雨、常规型降雨对边坡稳定性影响区别不大，但由于时效性的存在，其总会误判边坡失稳风险。故在实际边坡防治工作中，应该尽可能地考虑降雨特性对边坡稳定的影响。另外，大量研究表明，在基岩型浅层滑坡中，饱和渗透系数ks存在较强的变异性[4]，可将本文计算模型结合可靠度分析方法对边坡失效风险进行分析。

4 结论

(1)建立一种普遍型降雨模式，通过控制相关参数，统一了均匀性降雨、递增型降雨、递减型降雨、峰值型降雨等降雨类型。

(2)结合降雨入渗理论和无限边坡模型，建立了考虑降雨类型的基岩型浅层边坡稳定性分析方法。通过编制模块化程序进行计算，为变雨强下基岩型浅层边坡稳定性稳定性分析提供了一种实用而有效的思路。

(3)不同的降雨模式对边坡稳定性系数影响较大，具有明显的时效性。在实际工程中，都将降雨类型简化为均匀性必然将造成较大的误差。因而，考虑不同降雨类型是必要的。

[1] 黄润秋. 20 世纪以来中国的大型滑坡及其发生机制[J]. 岩石力学与工程学报, 2007, 26(3): 433-453. [HUANG R Q. Large-scale landslides and their sliding mechanisms in china since the 20th century[J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(3): 433-453. (in Chinese)]

[2] 石振明，赵思奕，苏越. 降雨作用下堆积层滑坡的模型试验研究[J]. 水文地质工程地质，2016, 43(4): 135-140. [SHI Z M, ZHAO S Y, SU Y. An experimental study of the deposit slope failure caused by rainfall[J]. Hydrogeology & Engineering Geology, 2016, 43(4): 135-140. (in Chinese)]

[3] 张群，许强，甯娜. 降雨条件下低缓浅层土质滑坡稳定性影响因素及耦合研究[J]. 水文地质工程地质，2014，41(5)：90-94.[ZHANG Q, XU Q, NING N. A study of the stability influence factors and coupling for inclined-shallow soil landslides under the condition of rainfall[J]. Hydrogeology & Engineering Geology, 2014, 41(5): 90-94. (in Chinese)]

[4] 陈君，王浩，戴强，等. 湖北恩施市降雨引发滑坡灾害的风险评价[J]. 中国地质灾害与防治学报，2016，27(1)：15-21.[CHEN J, WANG H, DAI Q,etal. Risk assessment of landslide hazard caused by rainfall in Enshi city[J]. The Chinese Journal of Geological Hazard and Control, 2016, 27(1): 15-21. (in Chinese)]

[5] 汤明高，许强，李九乾，等. 降雨诱发震后松散堆积滑坡的启动试验研究[J]. 水文地质工程地质，2016，43(4)：128-134.[TANG M G, XU Q, LI J Q,etal. An experimental study of the failure mechanism of shallow landslides after earthquake triggered by rainfall[J]. Hydrogeology & Engineering Geology, 2016, 43(4): 128-134. (in Chinese)]

[6] 覃小华，刘东升，宋强辉，等. 强降雨条件下考虑饱和渗透系数变异性的基岩型层状边坡可靠度分析[J]. 岩土工程学报，2017，39(6)：1065-1073.[TAN X H, LIU D S, SONG Q H,etal. Reliability analysis of bedrock laminar slope stability considering variability of soil saturated hydraulic conductivity under heavy rainfall[J]. Chinese Journal of Geotechnical Engineering, 2017，39(6)：1065-1073. (in Chinese)]

[7] 马世国，韩同春，徐日庆. 强降雨和初始地下水对浅层边坡稳定的综合影响[J]. 中南大学学报(自然科学版), 2014, 45(3): 803-810. [MA S G, HAN T C, XU R Q. Integrated effect of intense rainfall and initial groundwater on slope stability[J]. Journal of Central South University (Science and Technology), 2014, 45(3): 803-810.(in Chinese)]

[8] 张群，许强，易靖松，等. 南江红层地区缓倾角浅层土质滑坡降雨入渗深度与成因机理研究[J]. 岩土工程学报，2016, 38(8): 1447-1455. [ZHANG Q, XU Q, YI J S,etal. Rainfall infiltration depth and formation mechanism of slow-inclination soil landslides in Nanjiang[J]. Chinese Journal of Geotechnical Engineering, 2016, 38(8): 1447-1455. (in Chinese)]

[9] 汪丁建，唐辉明，李长冬，等. 强降雨作用下堆积层滑坡稳定性分析[J]. 岩土力学, 2016, 37(2): 439-445. [WANG D J, TANG H M, LI C D,etal. Stability analysis of colluvial landslide due to heavy rainfall[J]. Rock and Soil Mechanics, 2016, 37(2): 439-445. (in Chinese)]

[10] 马世国. 强降雨条件下基于Green-Ampt入滲模型的无限边坡稳定性研究[D]. 杭州：浙江大学，2014. [MA S G. Study on the stability of infinite slope based on Green-Ampt infiltration model under intense rainfall[D]. Hangzhou: Zhejiang University, 2014. (in Chinese)]

[11] Chen L, Young M H. Green-Ampt infiltration model for sloping surfaces[J]. Water Resources Research, 2016,42(7): 887-896.

[12] Ng C W W, Wang B,Tung Y K. Three-dimensional numerical investigations of groundwater responses in an unsaturated slope subjected to various rainfall patterns[J]. Can Geotech J, 2011, 38(5): 1049-1062.

[13] 罗渝，何思明，何尽川. 降雨类型对浅层滑坡稳定性的影响[J]. 地球科学(中国地质大学学报), 2014, 34(9): 1357-1363. [LUO Y, HE S M, HE J C. Effect of rainfall patterns on stability of shallow landslide[J]. Earth Science(Journal of China University of Geosciences), 2014, 34(9): 1357-1363. (in Chinese)]

[14] 刘果果. 川东红层地区降雨诱发浅层土质滑坡试验及数值研究[D].成都：成都理工大学，2016. [LIU G G. Rainfall experiments and numerical analysis of the shallow landslide in the red-bed area in East Sichuan[D]Chengdu: Chengdu University of Technology, 2016. (in Chinese)]