基于相位优化的干线双向绿波协调控制方法
2018-03-30李祥尘李进龙何梦辰
李祥尘,李进龙,何梦辰
(西南交通大学,交通运输与物流学院,成都 610031)
0 引 言
干线协调控制是缓解城市交通拥堵和减少交通延误的重要方式,也是减少交通排放的重要措施。干线上交叉口间的间距不均匀等因素,使得传统的绿波协调控制方法难以在干线上设置双向绿波,并且其绿波带的带宽较窄,绿波速度也难以符合干线设计速度的要求。
近年来,很多学者针对干线协调控制的局限提出了不少的优化策略。Xiangjie Kong等提出的双层控制策略能够利用实时的交通数据来调整干线协调控制的参数[1,2];Ma Nan 、Lin Guo和Baolin Ye等提出的左转相位提前关闭和延迟开放等措施能够在一定程度上增加干线双向绿波带的带宽[3-5];Jun Zhou利用图解法来进行实例设置干线双向绿波带也取得较为理想的效果[6];王俊刚等将绿信比协同优化考虑到干线协调控制模型中,通过改变干线上交叉口的绿信比来增加绿波带的带宽[7];Chengkun Liu和Guojiang Shen等将干线分为多段,对每段分别设置双向绿波,能够进一步增加协调控制的效果[8,9];裴玉龙等从干线协调控制系统方面对协调控制模型进行优化,能够提升干线上交叉口通行能力和减少交通延误[10];Pengpeng Jiao利用实时交通信息来预测短时左转流量,从而调整公共周期和绿信比,能够进一步缩短延误[11]。虽然这些方法能够增加干线协调控制的效果,但是其并没有最大限度地提升双向绿波带的带宽,并且绿波速度也难以符合干线的设计速度要求。
城市干线上各相邻交叉口间的间距往往是不均匀的,这使得干线双向车流到达交叉口的时刻和交叉口对应方向的绿灯放行时间难以匹配,从而增加了干线双向绿波设置的难度。针对这一情况,本文提出一种基于交叉口相位优化的干线绿波协调控制方法来增加干线协调控制的性能。该方法通过调整干线上每个交叉口的信号相位组成和信号相位顺序,来增加相邻交叉口沿干线双向相位差的调整区间,从而使得其与干线双向车流到达时刻更好地匹配,进而增加干线双向绿波带的带宽。本文以干线双向绿波带的带宽最大为目标,以每个交叉口的各个方向通行需求得到满足为限制条件,建立干线双向绿波协调控制的优化模型。案例分析指出,相较于传统的图解法,本文提出的方法能够设置更宽的双向绿波,减少车辆的交通延误和停车次数,并且新方法能够严格按照干线的设计速度来设置绿波速度。
1 交叉口信号相位优化分析
传统方法难以设置干线双向绿波的根本原因是交叉口沿干线双向车流的到达时间和对应方向绿灯时间难以匹配。由于干线上交叉口的间距无法调整,干线最优行车速度也比较固定,所以无法调整干线双向车流到达交叉口的时刻。因此,通过调整交叉口沿干线方向直行的绿灯时间来更好地匹配干线双向车流到达时刻是比较可行的。传统干线绿波协调控制方法中,各交叉口沿干线双向的信号配时往往是对称放行(见图1(a)的相位1和2)或是单口放行(见图1(b)的相位1和2),这使得相邻交叉口沿干线双向的相位差调整区间变得很小,几乎无法调整。但是,通过信号相位优化来增加相邻交叉口沿干线双向相位差的调整区间是可行的。
城市干线的交通量往往比较大,因此交叉口沿干线方向的左转车流不能够和对向的直行车流同时通行。这种情况下,交叉口沿干线方向的信号配时除了对称放行和单口放行之外,还有很多其他的信号相位组成形式。图1给出了交叉口主要的几种相位组成形式,横向为协调控制的干线,纵向为相交道路。由于本文重点讨论交叉口沿干线方向车流的信号相位,为了简化问题,相交道路进口道的直行和左转车流的绿灯时间在图1中不区分讨论,统一为相交道路的绿灯相位(图(a)、(b)、(c)中的相位3,子图(d)中的相位2和4)。
在图1中,(a)图为干线方向对称放行,交叉口沿干线双向直行的绿灯时间完全重合;(b)图为干线方向单口放行,交叉口沿干线双向直行的绿灯时间完全错开,但在两个连续的相位中通行;(c)图所示的相位组成形式表示交叉口沿干线双向直行的绿灯时间部分重合,部分错开;(d)图所示的相位组成形式表示交叉口沿干线双向直行的绿灯时间完全错开,并且不在两个连续的相位中通行。图1所示的相位组合形式能增加交叉口信号配时的灵活性,从而增加相邻交叉口沿干线双向相位差的调整区间,有助于干线双向绿波带的设置。

图1 交叉口信号相位优化形式Fig.1 Phase optimization plans
图2给出两个相邻交叉口信号相位优化前后双向绿波带设置示意图。其中图(a)中,两个交叉口沿干线方向都是对称放行;图(b)中,两个交叉口都采用图1(c)所示的相位组合形式。两个子图中的双向绿波速度(斜率)相同,公共周期相同,对应交叉口沿干线双向的绿灯时长相同。很明显,图(b)中的双向绿波带的带宽更宽。

图2 交叉口信号相位优化前后绿波效果Fig.2 Green wave bands before and after signal phase optimization
2 基于相位优化的干线双向绿波协调控制方法
2.1 干线双向绿波协调控制步骤
基于交叉口相位优化的干线绿波协调控制方法的步骤为:
(1)首先,根据交通流量和交叉口车道数量对每个交叉口进行信号配时,选取所有交叉口中周期最大交叉口的周期作为协调控制的公共周期。
(2)其次,在公共周期的前提下,计算干线上每个交叉口各个方向的绿灯时长。
(3)利用2.2节中的模型进行优化求解,得出各个交叉口沿干线上、下行的直行绿灯起始时刻,同时得出干线双向的绿波带带宽。
(4)在上一步骤结果的基础上,结合图1中交叉口相位组合形式,对每个交叉口的信号配时进行完善。
由于第三步中的模型考虑了每个交叉口各个方向车流通行时长,所以在理论上,第四步中得出的各交叉口信号配时能够满足各个方向车流的通行需求。
2.2 干线双向绿波协调控制模型
考虑一条干线上有N个交叉口,如图3所示。横向道路为需要进行协调控制的干线,每个交叉口在干线上的进口道都不允许左转车流和对向直行车流同时通行;纵向道路为相交道路(有N条相交道路)。干线双向绿波协调控制模型要在满足每个交叉口所有方向通行时长的前提下,使得双向绿波带的带宽最大。

图3 拥有N个交叉口的干线Fig.3 An illustrative arterial with N intersections
模型的输入变量为:①交叉口i相交道路车流的通行时长和行人穿过干线的最小绿灯时长由交叉口的信号配时给出;②交叉口i沿干线上行方向直行绿灯时长giu-t,下行方向直行绿灯时长,上行方向左转绿灯时长giu-l,下行方向左转绿灯时长gid-l,同样由交叉口的信号配时给出;③交叉口i和交叉口i+1之间的路段长度li,i+1;④干线设计行车速度v,也是绿波速度。
模型的输出结果为:①交叉口i沿干线上行方向直行绿灯起始时刻下行方向直行绿灯起始时刻tid-t;②干线上行方向绿波带的带宽bu,下行方向绿波带的带宽bd。
模型需要满足的限制条件有:
(1)对于干线上任意一个交叉口,干线的左转车流与对向的直行车流存在冲突;干线直行车流与相交道路车流存在冲突;干线左转车流与相交道路车流存在冲突。这些存在冲突的车流不能同时通行,因此存在实数m、n使得:
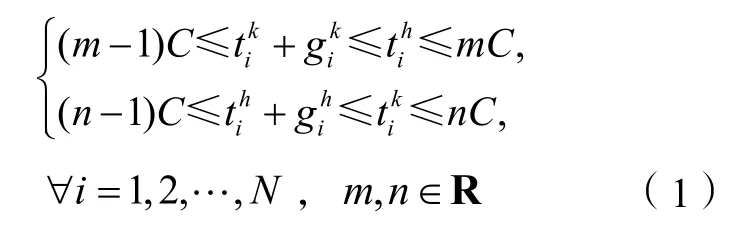
式中,C为公共周期,和tih表示在交叉口i中任意两个存在冲突的车流的绿灯起始时刻;gik和gih分别为对应方向车流的绿灯时长;m,n∈R表示m,n是实数,其作用是将各变量限制在一个周期内。
(2)对于任何一个交叉口i而言,沿干线双向直行车流调整时间不能妨碍相交道路的通行需求:
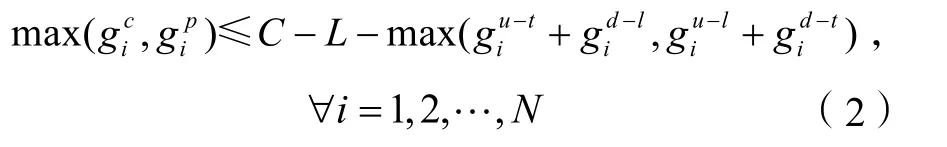
其中,L为周期内损失时间。
(3)为了保证上、下行方向的绿波带存在,相邻交叉口间的上、下行方向的相位差要满足以下限制条件:
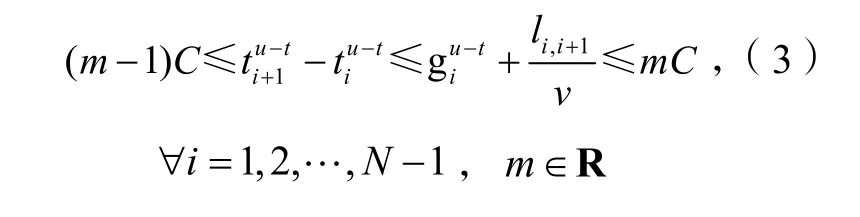



干线绿波带的带宽可以用绿波带的结束边缘和开始边缘之差来表示,上行方向绿波带的开始边缘为Bu,s,上行方向绿波带的结束边缘为Bu,e,下行方向绿波带的开始边缘为Bd,s,下行方向绿波带的结束边缘为Bd,e:


各个边缘的计算公式如下:
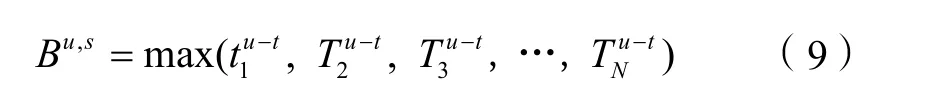

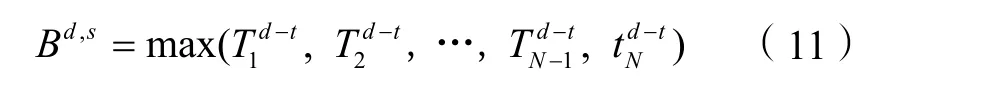


模型的目标是求出最大的双向绿波带宽。但是由于干线双向绿波协调控制有两条绿波带,并且二者之间是此消彼长的关系,若同时以两条绿波带的带宽最大为目标,将会形成双目标函数,模型的求解会比较困难。因此,本模型将干线上、下行方向的绿波带带宽之比固定为干线上、下行方向的各交叉口直行流量和之比,如下式所示:

模型的限制条件为式(1)~(8)、(14)。模型中有较多的变量,可以选择一个交叉口作为基准交叉口,该交叉口沿干线上、下行方向绿波的开始边缘差值定为ts,则其余交叉口沿干线上、下行方向绿波的开始边缘差值可以用ts、li,i+1/v和周期C的整数倍来表示。这样,模型的求解就可以简化为确定最佳的ts使得绿波带的带宽最大。
3 案例分析
3.1 案例设置
案例的协调控制干线共有5个交叉口,每个交叉口依次从左往右编号。协调控制干线为双向8车道,所有与协调控制干线相交的道路均为双向4车道。交叉口间的间距由左往右依次为:525m、375m、675m和425m,协调控制干线设计(绿波)速度为15m/s,每个交叉口沿干线方向的直行流量相同,干线在各个交叉口左转和右转比率为0.3,各相交道路流量输入为干线流量输入的三分之一。
在不同的流量大小输入情况下,分别用传统图解法和本文提出的基于相位优化方法进行干线双向绿波协调控制。按照两种方法的求解结果,利用VISSIM仿真软件进行仿真,并从双向绿波带的带宽、绿波速度、平均延误、平均旅行时间、平均停车次数几个方面来对结果进行分析评价。
3.2 案例结果及分析
图4为传统图解法和基于相位优化方法求解出来的双向绿波,每个子图的左侧为传统图解法求解的绿波,右侧为基于相位优化方法求解的绿波。图(a)表示公共周期长度为60s时,传统图解法得到的双向绿波带的带宽分别为15s和16s,绿波速度略低于15m/s;基于相位优化方法的双向绿波带的带宽为28s,并且绿波速度为15m/s。图(b)表示公共周期为100s时,传统图解法得到的双向绿波带的带宽为30s,绿波速度远高于15m/s;基于相位优化方法的双向绿波带的带宽为46s,并且绿波速度为15m/s。图(c)表示公共周期为150s时,传统图解法得到的双向绿波带的带宽为36s,绿波速度远高于15m/s;基于相位优化方法的双向绿波带的带宽为67s,并且绿波速度为15m/s。在不同的公共周期长度下,基于相位优化方法设置的干线双向绿波带的带宽都要大于传统图解法的绿波带带宽。同时,在不同公共周期长度下,基于相位优化方法得出的绿波速度都是15m/s,而传统图解法得出的绿波速度随周期变化的波动较大,较大地偏离干线设计速度。
在不同流量大小输入情况下,分别用传统图解法和基于相位优化方法对干线双向绿波进行求解,并用VISSIM仿真软件对得出的结果进行仿真和评价。图5给出了两种方法在不同流量大小输入情况下,车辆通过整条干线的平均延误。图6和图7分别为车辆通过干线的平均旅行时间和平均停车次数。两种方法的车辆平均延误、平均旅行时间和平均停车次数都随着流量增加而增加,但是基于相位优化方法的各项指标明显优于传统图解法。
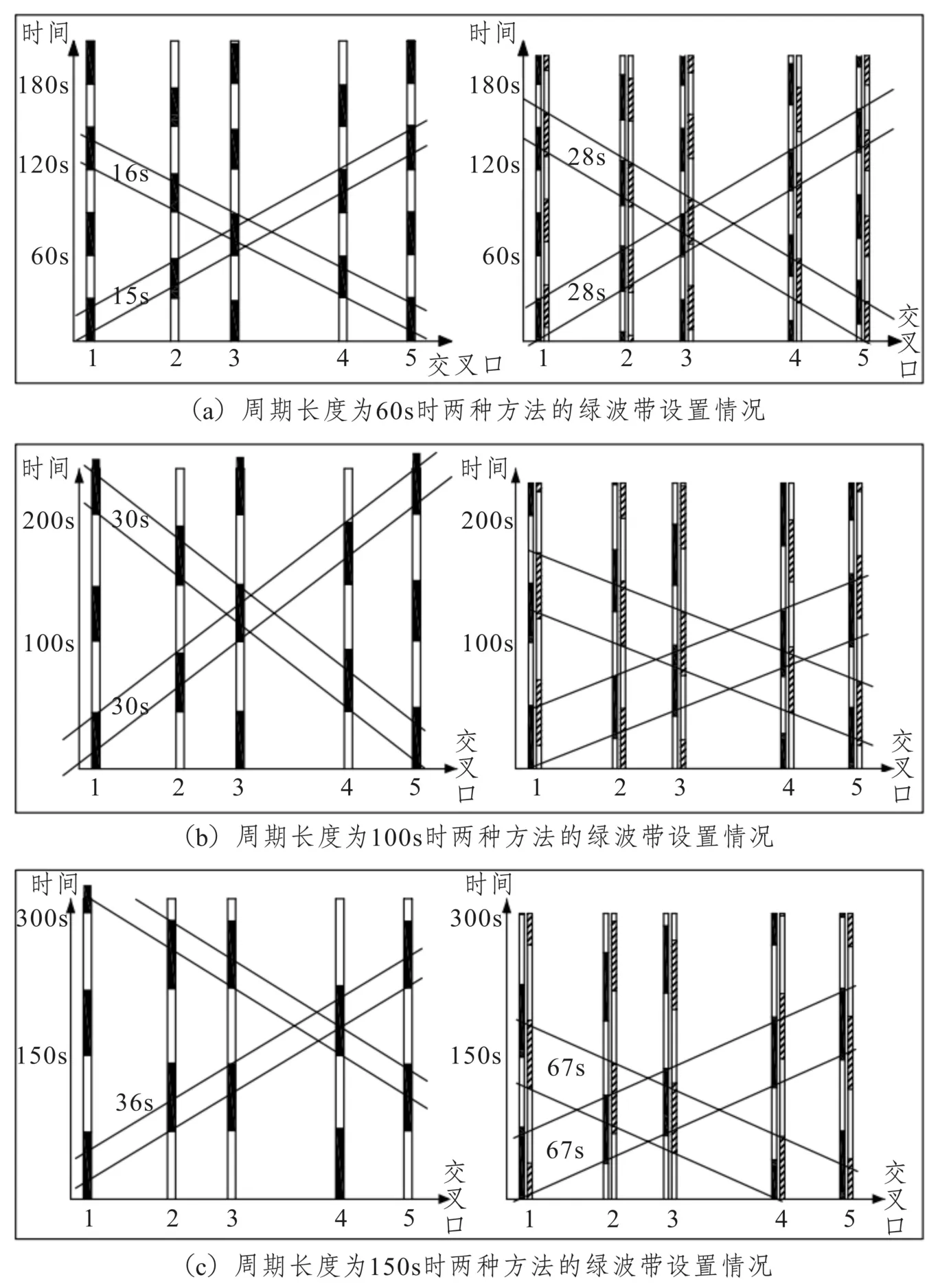
图4 不同周期长度下两种方法的双向绿波带设置情况Fig.4 Comparison of the green wave bands under difference cycle lengths

图5 两方法平均延误Fig.5 Comparison of average delay
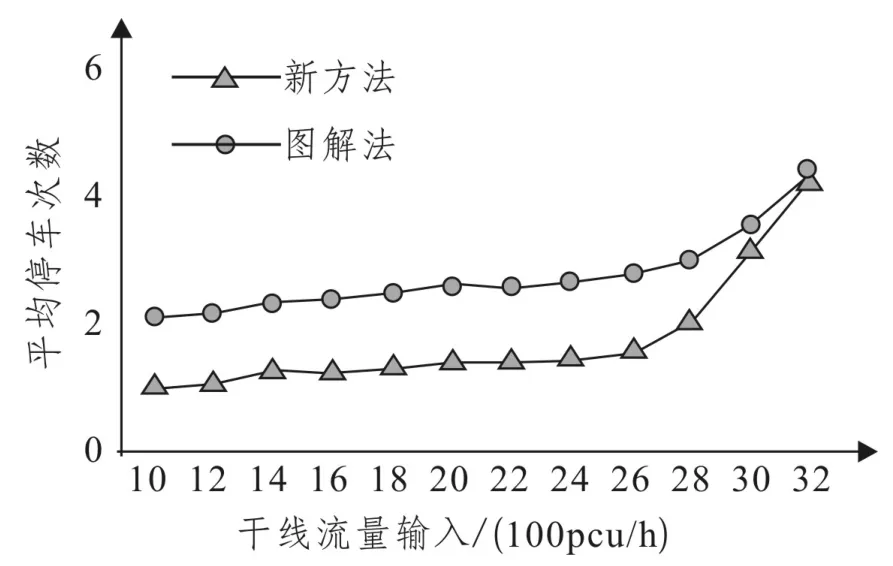
图6 两方法平均旅行时间Fig.6 Comparison of average travel time

图7 两方法平均停车次数Fig.7 Comparison of number stops
流量较小时,两种方法延误和停车次数均较小。随着流量增大,基于相位优化方法的优势明显显现出来。随着流量进一步增大,两种方法延误和停车次数都增大,并且二者之间的差距缩小,其原因是流量超出各交叉口的能力,整个干线都处于拥堵状态,协调控制无法发挥其作用。
4 结论与展望
本文提出的基于交叉口相位优化的干线绿波协调控制方法不仅能够增加干线双向绿波带的带宽,还能提升绿波速度对干线设计速度的适应性。相较于传统的图解法而言,基于相位优化方法能够极大地降低干线车流的交通延误,缩短车辆的旅行时间,减少车辆的停车次数,有助于缓解城市干线的交通拥堵,减少交通出行成本。
本文通过优化交叉口相位的组成和顺序来提升干线的协调控制的效果,该方法的思路在优化路网协调控制方面也存在较大的潜力,其具体效能有待进一步研究。
[1] KONG Xiangjie,XIA Feng,LIN Chuang,et al. Urban arterial traffic intelligent coordination control technique and its application[C]// Proceedings of the 8th World Congress on Intelligent Control and Automation,Jinan,2010:5042-5047.
[2] KONG Xiangjie,SHEN Guojiang,XIA Feng,et al. Urban arterial traffic two-direction green wave intelligent coordination control technique and its application[J].International Journal of Control,Automation,and Systems,2011: 60-68.
[3] MA Nan,SHAO Chun fu,ZHAO Yi. Study on coordination control with bandwidth optimization for signalized intersections in arterial systems[C]// 2010 International Conference on Optoelectronics and Image Processing,2010,425-430.
[4] GUO Lin,YANG Renfa,ZHANG Minjie. Arterial traffic two-direction green wave coordination control based on MATLAB graphical method[C]// 2015 2nd International Conference on Information Science and Control Engineering,2015:632-635.
[5] YE BaoLin,WU Weimin,ZHOU Xuanhao,et al. A green wave band based method for urban arterial signal control[C]// 2014 IEEE 11th International Conference on Networking,Sensing and Control(ICNSC),2014:126-131.
[6] ZHOU Jun. Traffic signal coordination control of city arterial road that based on graphic method[C]// 2011 International Conference on Electronic & Mechanical Engineering and Information Technology,2011: 3562-3566.
[7] 王俊刚,褚世新,余泉,等. 干线协调控制系统的绿信比协同优化模型研究[J]. 交通运输工程与信息学报,2005,3(2):13-18.
[8] LIU Chengkun,YONG Qin,LI Haijian,et al. Design of double green waves scheme for arterial coordination control[J]. Springer-Verlag Berlin Heidelberg,2013,309-315.
[9] SHEN Guo jiang,YANG Yong yao. A dynamic signal coordination control method for urban arterial roads and its application[J]. Frontiers of Information Technology &Electronic Engineering,2016:907-918.
[10] 裴玉龙,孙明哲,董向辉. 城市主干路交叉口信号协调控制系统设计研究[J]. 交通运输工程与信息学报,2004,2(2):41-46.
[11] JIAO Pengpeng,WANG Honglin,SUN Tuo. Real-time arterial coordination control based on dynamic intersection turning fractions estimation using genetic algorithm[J].Mathematical Problems in Engineering,2014, (3):1-10.
