多资源约束下车辆配送路径优化模型

吴正阳，鲁工圆,2，马驷,2

（1. 西南交通大学，交通运输与物流学院，成都610031；2. 综合交通运输智能化国家地方联合工程实验室，成都610031）

0 引 言

资源约束下的配送路线优化问题是在资源量变化的约束条件下对配送路线进行优化的问题。本文多资源指的是影响、限制车辆对配送路线进行规划选择的资源，例如车载能源、车载货物重量（体积）和车辆剩余可装货物重量（体积）等。本文研究在上述资源的消耗约束下寻找最高效的配送路线完成货物配送，属于车辆路径问题范畴。

车辆路径问题可以描述为：对一系列卸货点和（或）装货点规划适当的行车路线，使车辆按照路线有序地通过，并在满足一定的约束条件下达到一定的目标[1]。车辆路径问题最早由Dantzig和Ramser[2]于1959年提出，随后国内外学者对问题与模型进行了完善，提出多种算法对模型进行求解，并不停地对算法进行改进，提高模型解决问题的效率。Toth[3]等对车辆路径相关问题进行了定义，介绍了各种类型的车辆路径问题及其数学模型，包括了以车流为基础的模型、以物流为基础的模型和集覆盖模型等三类模型。

张维泽[4]等建立了带约束条件的物流配送问题的数学模型，运用改进的蚁群算法解决物流配送路径优化问题。刘志硕[5]等在分析VRP与TSP区别的基础上，构造了求解VRP的自适应蚁群算法。郎茂祥[6,7]构造了求解物流配送路径优化问题数学模型的遗传算法和混合遗传算法。符卓[8]对开放式车辆路径问题进行了研究，提出一种用于求解带装载能力约束的开放式车辆路径问题的禁忌搜索算法。周慧等[9]针对物流配送中动态车辆路径优化问题，综合考虑动态需求、路网影响、车辆共享、时间窗以及客户满意度，建立了多目标动态数学规划模型。石锐[10]通过引入时间轴，将时空网络模型应用到震后救援物资配送研究中，系统地解决了地震灾后特定时间段内物资分配最佳方案的求解问题。郭建红[11]建立了带时间窗的动态车辆路径优化模型，提出了采用两阶段法求解策略和改进型遗传算法。Yang[12]等提出在电动汽车电池续航里程限制且能在路网上资源增加点进行电池的充电或者更换的情况下，建立配送路线优化选择问题的混合整数规划模型。李宁[13]、何小锋[14]等分别提出不同的算法对带时间窗车辆路径问题进行了求解。宁涛[15]等针对动态环境下车辆路径问题，以最小化车辆数和配送里程、最大化载货率为目标，建立动态车辆路径问题的数学模型，提出了云自适应遗传算法。

多数已有文献中路网上的节点只包含仓库节点和客户节点，而本文的路网中有三类节点，包括仓库节点、客户节点和资源增加节点，Yang等在文献[12]中引入上述概念。具有这三类节点的路网更加接近实际路网的情况，能准确反映出各资源量在路网中的变化情况，对车辆在路网中所进行动作的描述更加准确。

1 问题描述

本文研究在车辆行驶过程中多种有限资源约束下，从配送中心（物流据点）用多辆汽车向多个需求点（顾客）送货的配送路线优化问题。零售商（客户）为了控制仓储成本，希望上游配货商选用少量多次的配送方式进行货物配送，一辆车通常需要服务多个客户点，车辆完成一次配送任务所需行驶的距离大大增加。为了防止车辆在配送途中因燃油不够而导致行驶距离增加的情况出现，所以在进行配送路径的规划时将加油站点增加到路网中去。

对于该问题建立无向图G=(N,E,W1,W2,W3)，其中G表示道路交通网络，N为路网上的节点集合，i,j,k∈N；E表示网络图上的弧集，e∈E。W1,W2,W3表示网络弧上的三个权值，分别为车辆从i到j所需要花费的时间w1(e)=ctij、行驶的距离w2(e)=dij和消耗的资源w3(e)=crij。在路网中，通过某条配送路径P所花费的时间为其中边e=(i,j)是组成路径P的一段弧，在该问题中需要将仓库点虚拟成起点o和终点d，如图1所示。

图1 网络构造Fig.1 Network topology

本文主要研究多资源约束对路线优化问题的影响。以车载能源量和车辆载重能力为资源约束，在给定每个客户的位置和需求量、车辆载重量、仓库位置情况下，以仓库为起点合理安排车辆路线，使所有车辆在满足运输需求的同时达到总旅行时间最少，并满足以下条件：

（1）满足资源量变化约束，车辆将车载资源消耗完之前必须到达资源增加点，并在资源增加点将车载资源量增加至饱和。

（2）每个客户点的需求必须满足，且只能由一辆车完成送货，车辆访问资源增加点的次数不限。

（3）配送车辆从仓库出发完成配送并回到该仓库。

2 多资源约束下配送路径优化模型

模型的目标函数为所有车辆从仓库出发完成配送任务回到出发仓库所花费的时间总和最少，可以简化为所有车辆完成配送任务所行驶的总时间最小。

2.1 多资源约束下的静态配送路径优化模型

2.1.1 数学模型

静态配送路径优化模型是以车流为基础建立的，并基于物理网络对车辆的状态进行描述，增加资源消耗约束条件。

（1）目标函数为所有车辆完成配送任务所耗的总时间最小：

式中，ctij为车辆经过弧(i,j)所需花费的时间，

ctij=dijs；s为车辆行驶速度；为0-1变量，车辆v经过弧(i,j)时取1，否则取0；N为所有节点的集合，V为车辆集合。

（2）约束条件

模型考虑流平衡约束、服务唯一性约束、资源量变化约束与变量取值约束等，以保证车辆满足配送路径中的限制条件。

① 流平衡约束，保证每辆车从仓库（起点o）出发，对客户进行服务后必须离开，最后返回仓库（终点d）：

② 服务唯一性约束，保证每个需求客户点只能被一辆车服务一次：

③ 弧上资源量变化约束，描述了邻接节点i,j间资源w的数量关系：

④ 点上资源量变化约束，描述了车辆离开节点时的资源量与到达该节点时的数量关系：

⑤ 变量取值约束：

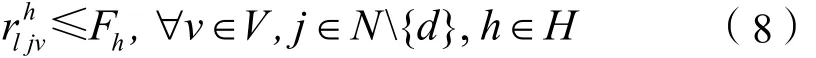
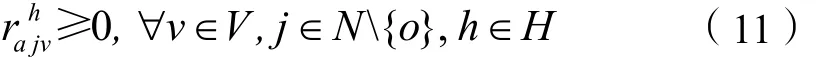
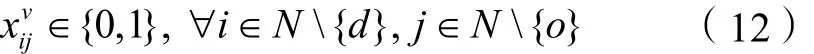
2.1.2 子回路问题的解决方法

由于允许车辆多次访问同一个资源增加点，所以最优配送路线就可能包含子回路。但是对资源量的描述是基于一维物理网络上的节点，无法表示出一个节点上的多个资源量状态，即不能求解具有子回路的配送问题。

配送路线中产生子回路的直接原因是车辆多次访问了资源增加点，所以将车辆多次访问一个资源增加点转化为车辆访问多个资源增加点，且每个资源增加点最多只能访问一次。对每个资源增加点增加与其相对应的虚拟资源增加点，且对应的个数应不小于在转化前车辆需要访问一个资源增加点的次数a，a通常为2。实际点与其相对应的虚拟点之间两两互不相通，如图2所示。

图2 物理网络改造Fig.2 Transformation of the physical network

通过以上处理，就可以用静态模型求解一般的配送路径优化问题。相关方面的专家学者还提出了其他解决子回路的办法，文献[12]通过改进载重约束条件，允许车辆对资源点进行多次访问。

2.2 多资源约束下的动态配送路径优化模型

动态配送路径优化模型基于时空网络建立，不存在静态配送路径优化模型中的子回路问题。时空网络模型首先由Hane[16]等人提出，用以解决航空调度的路径问题。基于时空网络的动态配送路径优化模型可以清楚地描述车辆在路网上的状态变化过程，图3展示了在单资源约束下，车辆在时空网络上的状态变化过程。

图3 时空网络的构建Fig.3 Construction of the space-time network

图3对一个包含4个节点3条弧的物理网络进行了时空网络的构建，车辆的最大资源储存量为4个单位。图（a）、（b）分别展示了车辆在物理网络和时空网络上的资源变化过程。[ct,cr] 中的ct、cr分别表示车辆在弧上的行驶时间和资源消耗，（ra,rl）中的ra、rl分别表示车辆到达、离开节点时的资源量。以时空网络路径③为例，车辆从（A，3）出发，出发时资源量为4个单位，经过2个单位的行驶时间，消耗掉2个单位资源量，到达点（B，5），到达点（C，6）时的资源量为1个单位，加满油后，车辆离开时的资源量为4个单位。

动态配送路径优化模型如下：

（1）目标函数：

（2）约束条件：

① 流平衡约束：

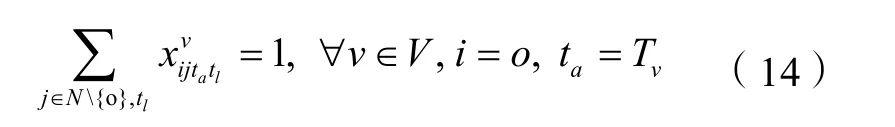
② 服务唯一性约束：

③ 弧上资源量变化约束：

④ 点上资源量变化约束：

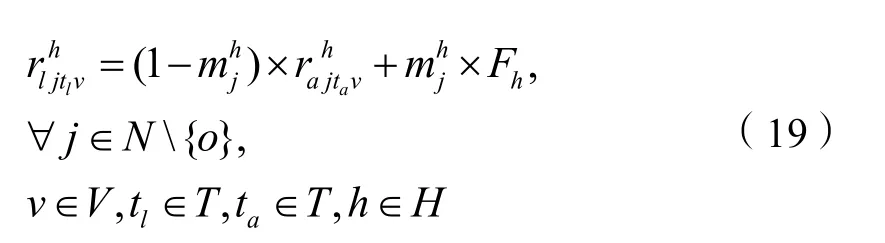
⑤ 变量取值约束：

式中，ctijtlta为通过时空网络弧(i,j,tl,ta)所需花费的时间；为0-1变量，车辆v通过时空网络弧(i,j,tl,ta)时取1，否则取0。为车辆v在时刻ta（tl）到达（离开）点j时的资源h的数量；T为时间集合。在时空网络模型中，Tv、T'分别为研究时间域的起点与终点。v

3 算例实验

本文两个算例都是在CPU为Intel（R）Core（TM）i7-4710HQCPU@2.5GHZ、内存为16GB的计算机上，采用商业优化软件IBM ILOG CPLEX 12.6.2的OPL（Optimization Programming Language）编程语言编程求解。

3.1 算例1

物理网络结构如图4所示，相邻点间的距离dij（单位为km）如表1所示。

图4 物理网络结构图Fig.4 Network structure

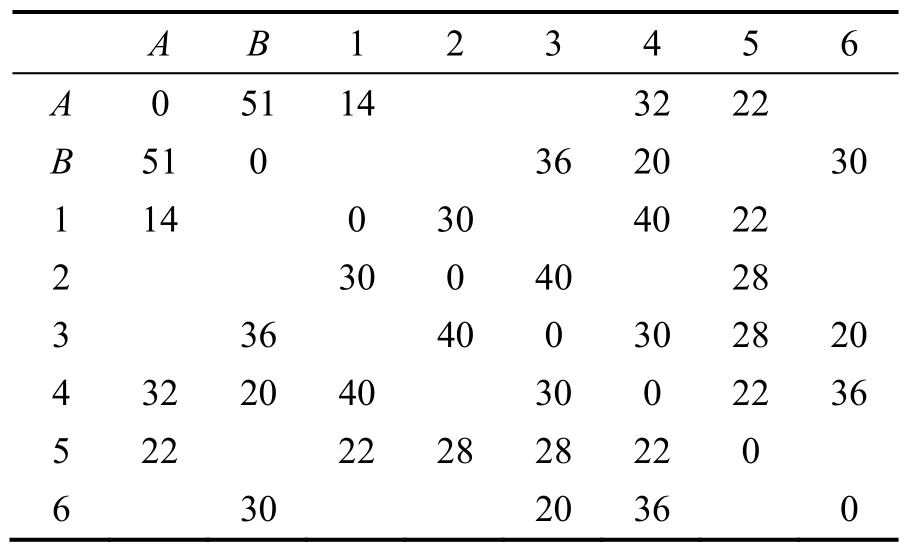
表1 各节点间的距离Tab.1 Distance information

车辆的额定载重量U=4t，每个客户点的需求量qi如表2所示。。车辆从仓库出发时的初始能源量与车辆的最大能源装载量相同，可供车辆行驶距离为90km。车辆可以从仓库A（B）出发，最后回到仓库A（B）。

表2 客户点的需求量Tab.2 Demand at each customer points

3.1.1 算例1基于静态配送优化模型的求解

车辆经过弧(i,j)的时间消耗ctij=dij/s，能源消耗量与车辆行驶距离成正相关，所以取这里取s=1km/min，通过软件CPLEX12.6.2，用静态模型求解配送最优路径。

当车辆从仓库A出发时，求得最优路径P=（A,1,2,5,3,4,A），如图5所示，目标函数z=162min。图中括号内数值依次表示到达时油量、出发时油量与出发时剩余载重量。

图5 从仓库A出发的最优配送路径Fig.5 Optimal delivery path from depot A

当车辆从仓库B出发时，不增设虚拟资源点，静态模型无法求解出最优配送路线，所以需要对配送网络进行改进。参照上述改进的方法，取车辆访问资源点的次数为a=2，即增设一个虚拟资源增加点，如图6（a）所示。

用静态模型对改进后的配送网络进行求解，得出最优配送路径P=（B,3,5',2,1,5,4,B），目标函数为186 min，如图6（b）所示。图中括号内数值意义与图5中相同。

图6 从仓库B出发的最优配送路线Fig.6 Optimal delivery path from depot B

3.1.2 算例1基于动态配送优化模型的求解

出发时刻Tv和到达终点时刻Tv'分别设为第1min末与第190min末。通过软件CPLEX12.6.2，用动态模型求解配送最优路径，如图7所示。图中括号内数值依次表示到达时间、出发时间、到达时油量、出发时油量与出发时剩余载重量。

当车辆从仓库A出发时，求得最优路径P=（A,4,3,5,2,1,A），目标函数z=162min，配送路径如图7（a）所示。

当车辆从仓库B出发时，求得最优路径P=（B,4,5,1,2,5,3,B），目标函数z=186min，配送路径如图7（b）所示。

图7 从仓库A、B出发的最优配送路线Fig.7 Optimal delivery path from depot A and B

3.2 算例2

车辆的最大能源装载量与车辆从仓库出发时的初始能源量相同，可供车辆行驶距离为30 km。最少需要3辆车进行货物配送。取s=1km/min，能源消耗量取值为。通过软件CPLEX12.6.2，用静态模型求解配送最优路径，详细情况如表4所示。

将上述三个方案进行比较，配送方案为4辆车的行驶时间最短，所以最优方案为4辆车的配送方案，最优配送路径如图8所示，图中括号内的数值依次表示车辆编号、到达时油量、出发时油量与出发时剩余载重量。

表3 各节点的位置坐标与货物需求量Tab.3 Position and demand of each node

表4 各使用车数下所对应的目标函数和车辆路径Tab.4 The objective function and path corresponding to the number of vehicles used

图8 最优配送路径Fig.8 Optimal delivery path

用动态配送路径优化模型在求解算例2时，以GAP=10%为求解器计算终止条件，输出求解结果。在该算例中CPLEX耗时31min达到GAP8.35%，目标函数值121min。

4 结 论

（1）本文所建立的资源约束下配送路径优化静、动态模型，能够描述与解决在车载能源量、车辆载货能力等多资源约束下的车辆配送路线优化问题，可统一描述资源量增加和减少两种情况。

（2）多资源约束下的静态配送路径优化模型中针对车辆各种资源状态参数在物理网络中进行标记，通过增加虚拟资源点，解决了该类模型中存在的子回路问题。

（3）多资源约束下的动态配送路径优化模型基于时空网络建立，能够有效避免子回路问题，对问题的描述及求解结果更加直观准确。动态模型以扩大模型规模为代价丰富了车辆配送路径选择方案，同时能准确得到车辆到达、离开客户点的时间。

对于具有NP-Hard特征的VRP问题，尤其是考虑多种资源约束情况下，求解器在网络规模扩大导致问题规模变大时存在效率问题，进一步研究工作重点在于针对该模型寻找高效的求解算法。

[1] 赵燕伟，张景玲，王万良. 物流配送的车辆路径优化方法[M]. 北京：科学出版社，2014.

[2] DANTZIG G B，RAMSER J H. The truck dispatching problem [J]. Management Science，1959，6（1）：80-91.

[3] TOTH P，VIGO D. The vehicle routing problem [M].Society for Industrial and Applied Mathematics，2002.

[4] 张维泽，林剑波，吴洪森，等. 基于改进蚁群算法的物流配送路径优化[J]. 浙江大学学报：工学版，2008，42（4）：574-578.

[5] 刘志硕，申金升，柴跃廷. 基于自适应蚁群算法的车辆路径问题研究[J]. 控制与决策，2005，20（5）：562-566.

[6] 郎茂祥. 基于遗传算法的物流配送路径优化问题研究[J]. 中国公路学报，2002，15（3）：76-79.

[7] 郎茂祥，胡思继. 用混合遗传算法求解物流配送路径优化问题的研究[J]. 中国管理科学，2002，10（5）：51-56.

[8] 符卓. 带装载能力约束的开放式车辆路径问题及其禁忌搜索算法研究[J]. 系统工程理论与实践，2004，24（3）：123-128.

[9] 周慧，周良，丁秋林. 多目标动态车辆路径问题建模及优化[J]. 计算机科学，2015，42（6）：204-209

[10] 石锐. 基于时空网络的震后救援物资配送模型研究[D].上海：华中科技大学，2011.

[11] 郭建红. 带时间窗的卷烟物流配送动态车辆路径优化方法研究[D]. 北京：北京交通大学，2013.

[12] YANG J，SUN H. Battery swap station location-routing problem with capacitated electric vehicles [J]. Computers& Operations Research，2015，55：217-232.

[13] 李宁，邹彤，孙德宝. 带时间窗车辆路径问题的粒子群算法[J]. 系统工程理论与实践，2004，24（4）：130-135.

[14] 何小锋，马良. 带时间窗车辆路径问题的量子蚁群算法[J]. 系统工程理论与实践，2013，33（5）：1255-1261.

[15] 宁涛，陈荣，郭晨，等. 一种基于云计算环境的动态车辆路径问题解决策略[J]. 交通运输工程与信息学报，2015，13（3）：1-6.

[16] HANE C A，BARNHART C，JOHNSON E L，et al. The fleet assignment problem：solving a large-scale integer program [J]. Mathematical Programming，1995，70（1-3）：211-232.