铁路客运网络结构评价研究

朱倩，倪少权

（1. 西南交通大学，交通运输与物流学院，成都 610031；2. 西南交通大学，全国铁路列车运行图编制研发培训中心 成都 610031；3. 综合交通运输智能化国家地方联合工程实验室，成都 610031）

0 引 言

2016年，国务院常务会议审议并通过了《中长期铁路网规划》，其发展目标为至2020年，铁路网规模达到15万km，覆盖80%以上的大城市，至2025年，铁路网规模达到17.5万km。随着路网规模的扩大及自动化水平的提高，有必要对区域客运网络结构进行科学合理的评价，针对评价结果对其进行相应地改善，进而使客运网络的建设与地区社会经济发展及旅客交通需求相适应，对于提高社会资源利用率、推进国民经济的发展具有举足轻重的意义。

目前针对路网结构的评价方法主要有两类：一类是数据包络分析法[1,2]，一类是综合评价法[3,4]。数据包络分析法（DEA）要求决策单元的“市场环境”相同，输入和输出也相同，当投入产出数据无法定量计量时，该方法无法对其进行优劣性评价，超效率数据包络分析（SE-DEA）[2]仅仅能够解决传统DEA法当决策单元多个有效或全部有效时无法进一步区分其优劣性的问题，不能避免DEA法固有的缺陷。目前用于评判路网结构的综合评价方法仅有AHP-Fuzzy模糊评判模型，该方法利用层次分析法确定评价体系中各评价指标的权重，用模糊学理论对评价结果进行定量计算，但是层次分析法确定权重的缺点是过于偏重决策专家的主观判断，获得的评价指标的权重具有较强的偏好性，说服力不强。

国内外关于路网结构评价的研究多集中在城市道路网及轨道交通网络规划的问题上，在铁路客运网络结构评价方面鲜有涉及。本文针对铁路客运网络结构的特点，从路网规模、运营效果及与区域的协调程度这三个方面系统地建立了铁路客运网络结构评价指标体系，提出了基于粗糙集、层次分析法（AHP）及模糊学理论（Fuzzy）的综合评判模型。采用层次分析法确定客运网络结构评价指标体系的主观权重，粗糙集方法确定客观权重，运用优化模型求解综合权重，最后建立模糊评判关系矩阵对客运网络结构进行综合评价。

1 铁路客运网络结构评价指标体系构建

我国铁路客运网络具有较强的复杂性，其目标是缩短时空距离、提高区域内出行可达性、适应和引导区域发展、促进区域经济一体化并提高区域的整体竞争力。铁路客运网络结构评价指标体系的建立是结合路网内各评价指标的实际意义以及相互间的作用关系，按照完备性、独立性、简洁性、可比性和可操作性的原则，建立能够全面、客观评价铁路客运网络结构及功能的指标体系并构成递阶层次体系。所建立的铁路客运网络结构评价指标体系包括路网规模、运营效果及与区域的协调程度三个层面，如图1所示。

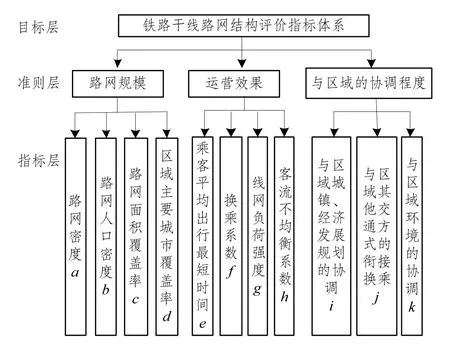
图1 铁路客运网络结构评价指标体系Fig.1 Evaluation index system of railway passenger transport network

各评价指标的含义及计算方法如下所示：

（1）路网密度a

路网密度是指区域内铁路干线总长与区域面积之比。对区域而言，区域内部对外部交通联系的便捷程度与路网密度成正比，但路网密度过大，会增加工程投资，使行车组织复杂化，并造成线路通行能力以及能源资源的浪费。因此，合理均衡的铁路路网密度能够体现一个区域内铁路建设的质量和水平，是评价铁路路网结构的理想指标：

式中，L为区域内所有铁路线的总长度，km；F为区域面积，km2。

（2）路网人口密度b（km/万人）

路网人口密度是指区域内铁路干线总长与总人口的比值，表示每万人占有的铁路干线长度。在对不同区域的铁路路网结构进行评价时，由于区域总人口数不同，因此出行需求量也不同，进而对于线路长度的要求也存在差异。因此，合理的人均线路里程能够满足区域内人口的交通需求又不会造成铁路运能的浪费，能够对路网结构进行科学的评判：

式中，N为区域内总人口数，万人。

（3）路网面积覆盖率c

路网面积覆盖率表示路网在规划区域内吸引客流的能力，也在一定程度上反映客运网络的可达性。该指标为定量指标，可以表示为：

式中，Q为客流吸引区域面积，km2。

（4）区域主要城市覆盖率d

区域主要城市覆盖率是指在线网连通区域内，主要城市的换算个数与规划区内主要城市换算个数的比值。可按照重要程度对区域网络内的城市进行分类，计算城市个数并通过加权折算为当量值。作为定量的效益型指标，其值越大越好，可以表示为：

式中，H为连通主要城市换算个数；S为规划区主要城市换算个数。

（5）乘客平均出行最短时间e

乘客平均出行最短时间是指乘客以铁路方式出行的平均最短时间，用以评价铁路线网的修建对居民出行花费时间的改善程度，同时也反映了整个区域铁路客运网络的运行效率。该指标为定量指标，可以表示为：

式中，tij为第i区域到第j区域的干线铁路最小出行时间；Qij为第i区到第j区的铁路出行分布量。

（6）换乘系数f

换乘系数是指干线铁路线网出行人次与换乘人次之和除以线网总出行人次。该指标用来衡量乘客出行便捷程度及铁路客运网络布线布站的合理性。换乘系数越小，表明直达程度越好。该指标为定量指标，可以表示为：

式中，C为出行人数；B为换乘人数；D为出行人次。

（7）线网负荷强度g（万人次/日km）

线网负荷强度用来衡量运量与运能是否相适应，它反映了铁路线网单位长度承担的客流量，用以评价铁路客运网络的运营和经济效益。该指标为定量指标，用铁路线网日均客流量R（万人次/日）与客运线网总长度L（km）的比值来计算，表达式为：

（8）客流不均衡系数h

客流不均衡系数指铁路客运网络各区间各线全日客流断面的最大值与平均值之比。反映干线铁路路网承担客流的均衡程度，用以评价客运网络的运营效率。作为定量指标，在客流预测结果的基础上，利用下列公式计算：

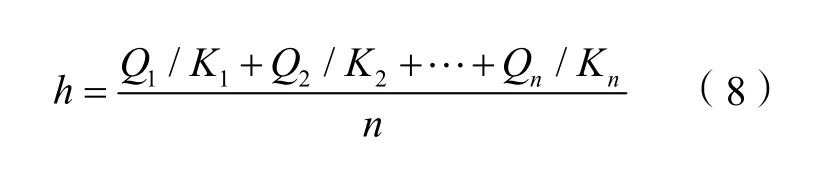
式中，Q1～Qn为各线全日双向最大断面流量之和；K1～Kn为各线客流量的平均值，为各全日断面客流量之和除以断面数量。

（9）与区域城镇、经济发展规划的协调i

区域内铁路客运网络的建设应该与城镇布局、经济发展相适应，同时进一步推动区域经济合作，促进经济联合发展，提高区域内的综合竞争力。该指标为定性指标。

（10）与区域内其他交通方式的协调j

铁路客运线路应注重与其他交通方式的换乘衔接，与区域内城市轨道交通及空中交通网、道路交通网、水运交通网等交通方式之间能够有良好的协调。该指标为定性指标。

（11）与区域环境的协调k

我国人均资源占有量少，生态环境比较脆弱，区域内的铁路客运网络应该注意资源节约、环境保护，体现科学发展观，“两型社会”的建设要求。该指标为定性指标。

2 粗糙集-AHP-FUZZY综合评判模型

评价指标体系中的每一种指标只能从反映铁路客运网络在某一方面的优劣，各网络中不同指标的优劣排序也不同，因此需要对客运网络进行综合评价，将评价指标及评价结果用同一个标准尺度来衡量。铁路客运网络的综合评价包括权重的确定及指标的综合评价两部分。

2.1 评价指标综合权重

（1）AHP确定主观偏好权重

①构造判断矩阵A

采用1～9比率标度法，对不同指标进行两两比较构造判断矩阵，能够将主观判断数量化，如表1所示。

表1 要素比较标度法Tab.1 Scales of element comparion

判断矩阵表达式为：

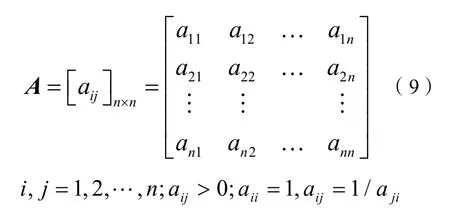
②采用“方根法”来求解判断矩阵A的特征向量及其对应的特征值。先计算每一行元素的乘积Mi，即

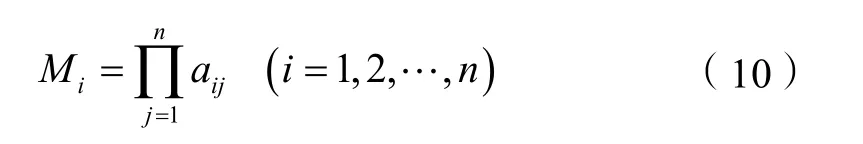
再计算Mi的n次方根Wi*将Wi*归一化，可得权值向量ωsi及最大特征向量λmax，即：

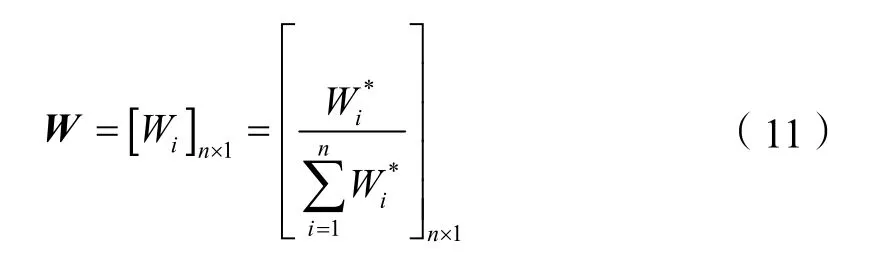
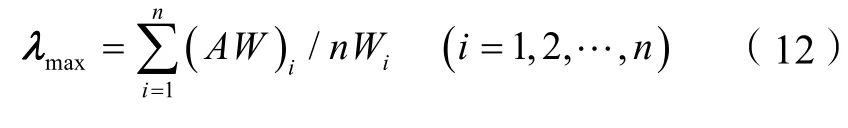
③对A进行一致性检验

确认A是否为最终权值向量。CI=（λmax-n） /（n-1）,CR=（CI）/（RI），RI为平均随机一致性指标如表2所示，当CR＜0.1时，认为矩阵具有满意的一致性。

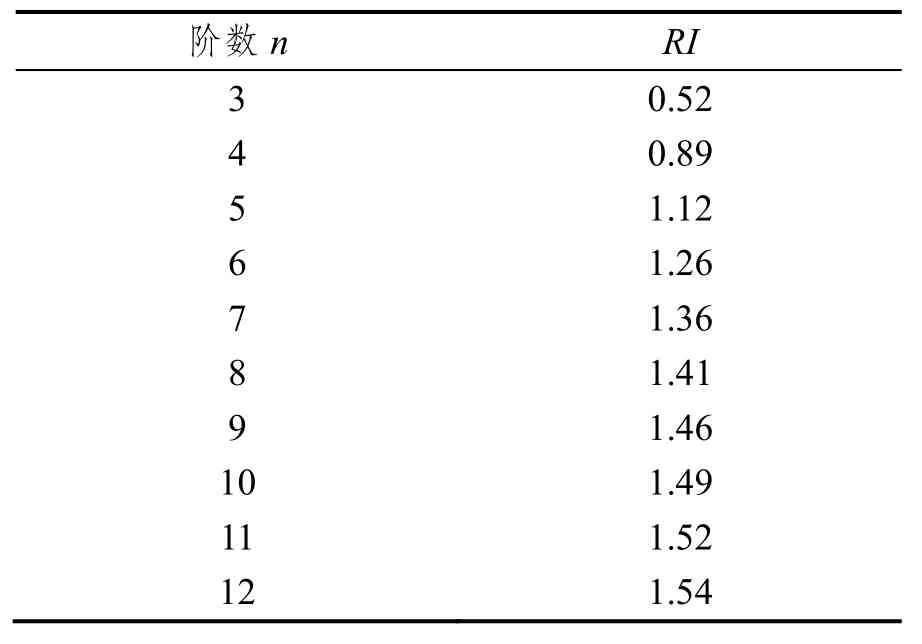
表2 平均随机一致性指标Tab.2 Average random consistency index

（2）粗糙集确定客观权重

应用粗糙集理论确定铁路客运网络评价指标客观权重的过程如下：

①信息系统

信息系统S是一个系统（U,A），其中是有限非空集，称为论域或对象空间，U中的元素称为对象；也是一个非空有限集，A中的元素称为属性，对于每个a∈A，有一个映射a:U→a（U），且称为属性a的值域[5]。

知识库中知识（属性）并不是同等重要的，甚至其中某些知识是冗余的，知识约简就是在保持知识库分类能力不变的条件下删除其中不相关或不重要的知识[6]。

定义1 令R为一族等价关系，r∈R，若则称r为R中不必要的；否则称r为R中必要的。如果每一个r∈R都是R中必要的，则称R为独立的；否则称R为依赖的[7]。

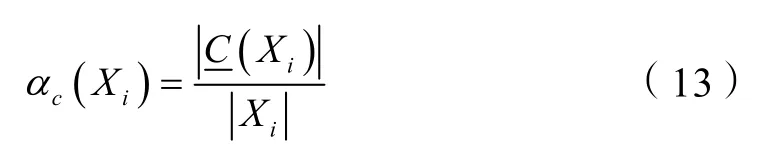
则全部决策类的近似质量为：

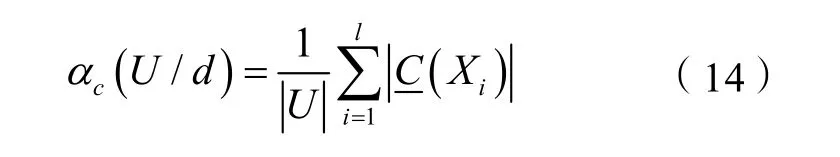
式中，αc（U/d）表示用条件属性集合C中的信息来近似U/d的近似质量。如果属性子集P⊆C是C的约简，则用属性集合P的信息来近似U/d的近似质量与用属性集合C中的信息来近似U/d的近似质量应该是相同的[7]。

②确定评价指标重要性

首先建立关系数据模型，然后利用粗糙集理论确定每个评价指标的权值。

从最低一层指标开始，建立其对父指标的制式表达系统（KRS），各子指标即构成条件属性集合C，设C=｛C1,C2,…,Cn｝，父指标即为决策属性D，设D=｛y｝。对知识表达系统进行量化处理，删除重复行。计算知识RD对知识RC的依赖程度，即评价指标集合C对决策属性指标y的依赖性：

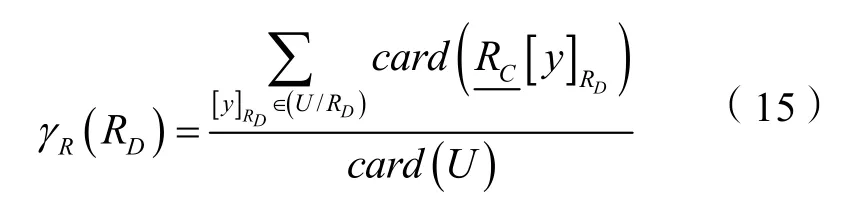
对每个评价指标ct，计算知识RD对知识RC-（Ct）的依赖性：

计算第i种评价指标的重要程度：

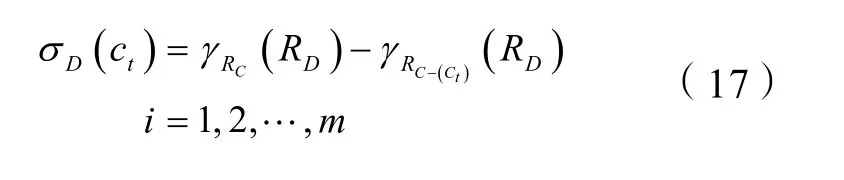
计算第i种指标的权系数为：

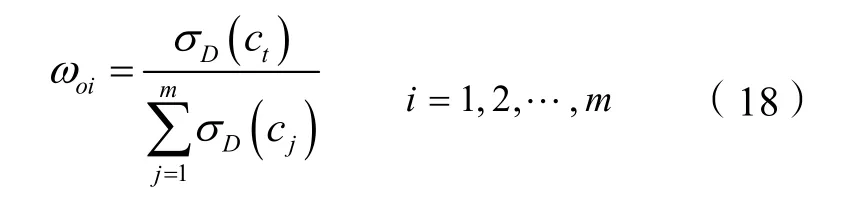
③指标客观权重计算

利用上述方法分别求出各指标对上一级指标的权重后，然后从上一级开始，自上而下的求出各级指标关于评价目标的客观权重，计算公式为：

式中，aj是一级指标相对于评价目标的权重，bij是二级指标相对于一级指标的权重。

（3）综合权重求解

① 建立最优化模型

设S=（U,A,V,f）是一个信息系统，ωsi、ωoi分别为属性ai的主观权重和客观权重，ωi为两者的综合权重，0≤ωoi≤1，0≤ωi≤1，i=（1,2,…,m），建立最优化模型：

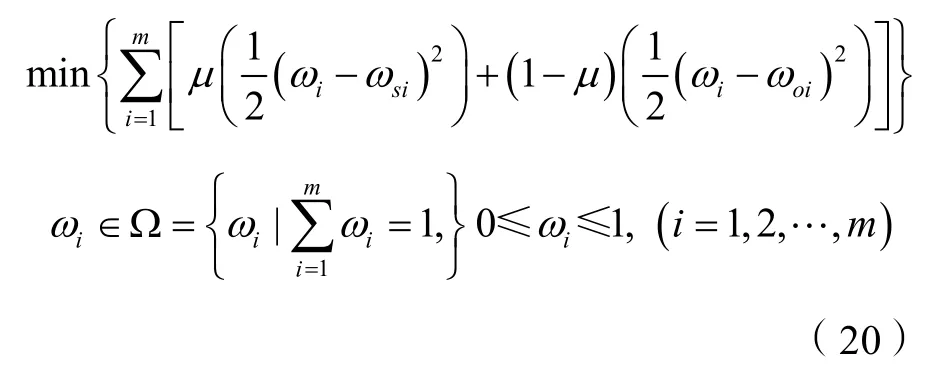
其中，0≤μ≤1。

② 最优化模型求解

作Lagrange函数：

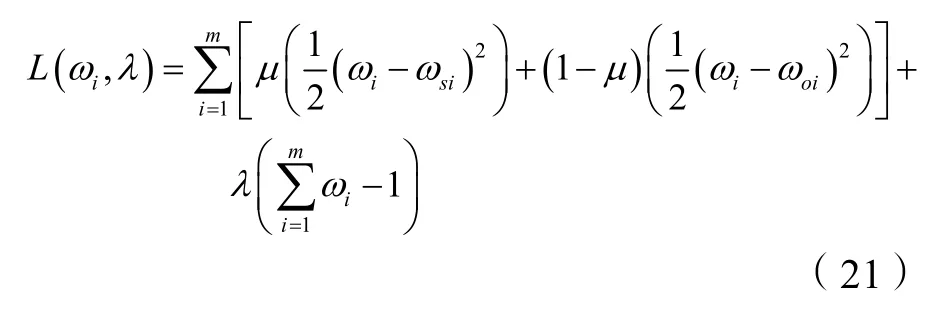
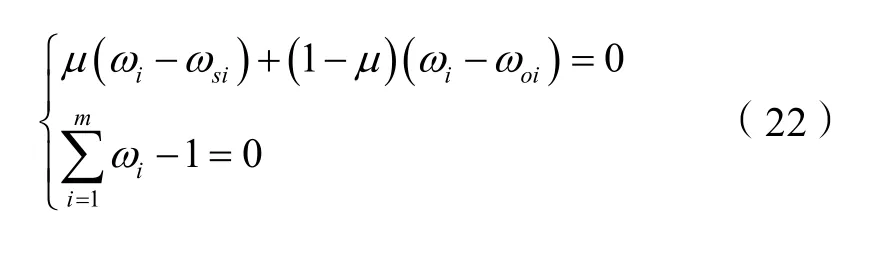
解此方程组得：

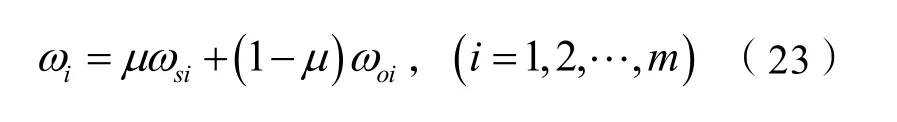
2.2 隶属函数构建

建立铁路客运网络评价的因素集和评语集，令因素集和为U=｛U1,U2,…,Um｝，其中Um表示第m个评价指标的取值。令评语集V=｛v1,v2,…,vm｝，其评价等级={较好，好，一般，较差，差}，并对其赋值为V=｛0.1,0.3,0.5,0.7,0.9｝。确定因素论域U和评语论域V之间的模糊关系，用模糊矩阵R表示。模糊关系矩阵R表示每一个评价指标对铁路客运网络不同评价等级的隶属程度，本研究采用线性隶属函数：

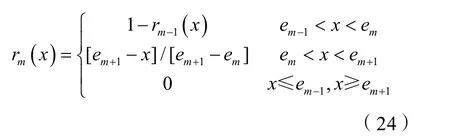
式中：x为评价因子的实际值；e为分级评级值；r为评价因子的隶属度。

2.3 模糊综合评判

将模糊向量ω和模糊关系矩阵R进行复合运算，得到综合评价模糊子集B，最终确定铁路客运网络综合评价结果：

式中，运算符号“◦”为合成算子，通常采用普通矩阵的算法或模糊矩阵合成算法，模糊矩阵合成算法按照最大最小运算法则进行，能够突出隶属度的很大或者很小。

3 实例分析

对10个区域的铁路客运网络结构进行评价，前文已经建立了铁路客运网络结构评价体系如图1所示。令条件属性集合A=｛a,b,…,k｝表示图1中所有的评价指标，令对象集合U=｛u1,u2,…,u10｝表示待评价的10个区域的铁路客运网络，令F表示决策属性对每个评价指标的属性值用“差”、“一般”、“良”和“优”四个等级衡量，分别用数值1、2、3、4来表示，构建如表3所示的初始信息系统S。

表3 知识表达系统STab.3 Knowledge expression systemS

对知识表达系统进行计算得到各评价指标的重要性σD（ci），并对其进行归一化处理，计算第i种评价指标的权系数λi如表4所示：

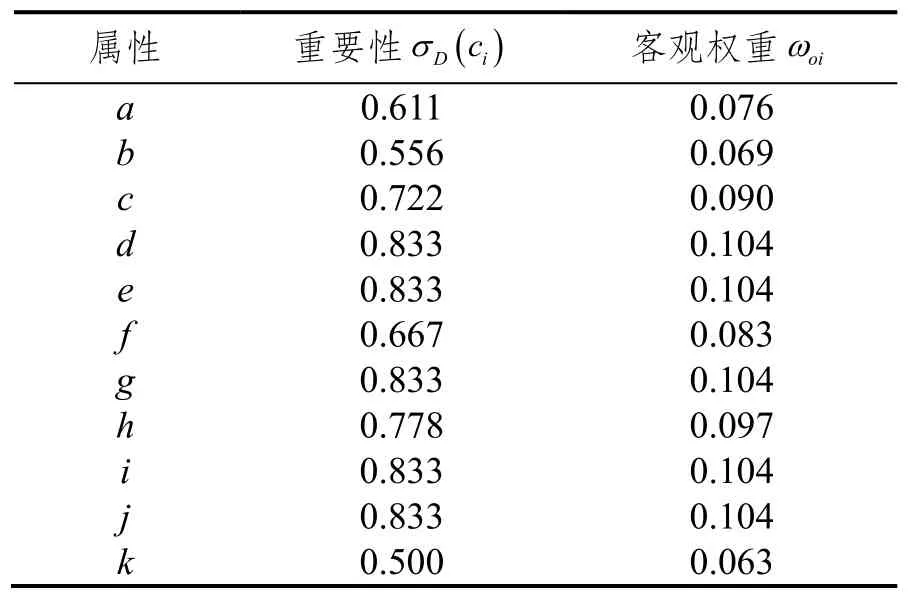
表4 评价指标重要性及权系数Tab.4 Importance and weight of each evaluation index

以上海铁路局管辖的铁路客运网络结构为例，根据评价指标确定综合权重的计算方法，利用层次分析法计算得到的主观权重ωsi、利用粗糙集方法计算得到的客观权重ωoi及利用最优化模型得到的综合权重ωi（取主、客观权重系数之比为黄金分割数，即μ=0.382）如表5所示：

表5 评价指标主、客观权重及综合权重列表Tab.5 The weights of subjective, objective and comprehensive evaluation indexes

计算得到各评价因子对评价标准的隶属度为：

得到评价结果：

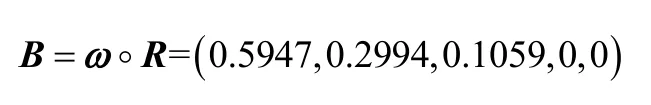
该铁路客运网络结构以59.47%的可信度隶属于“很好”，以29.94%的可信度隶属于“好”。因此上海铁路局的铁路客运网络结构处于较好的水平，尤其在各路网人口密度、路网面积覆盖率、乘车系数及城镇发展规划协调这四个指标上表现优异。铁路局的客运网络结构评价结果如表6所示：

表6 各铁路局管辖范围内的客运网络结构评价结果Tab. 6 Evaluation results of passenger network structure of each railway bureau

由此可以看出，位于华东、华中、华北地区的铁路局管辖的铁路客运网络结构均处于一般及以上水平，位于华南、西南、西北及东北地区的铁路局（除广铁公司外）管辖的客运网络结构均处于一般及以下水平。

4 结 论

本文基于铁路客运网络结构的特点及运营目标，建立了系统全面的评价指标体系，结合层次分析法、粗糙集理论与模糊学原理构造基于粗糙集-AHP-Fuzzy的铁路客运网络结构综合评判模型。该方法在确定权重时将主、客观权重相结合，具有较强的说服力，利用模糊学方法能够通过精确的数字对具有模糊信息的评价对象进行科学、合理的量化评价。铁路网络的系统性比较强，对客运网络结构的评价能够对既有网络的运行质量进行客观合理的判断，针对相关问题采取有效的措施提高路网结构的运输能力和运行效率，并对未来客运网络进行合理地规划，从而充分利用现有交通资源，切实提高整个路网承载能力，优化完善服务方式与运营水平。

[1] 张玉召，严余松，江南，等. 基于DEA的城市轨道交通规划线网综合评价研究[J]. 铁道工程学报，2010，08：96-99.

[2] 张桐，金键，沈犁，等. 基于SE-DEA的城市轨道交通线网规划方案优选[J]. 铁道标准设计，2015，59（09）：33-36.

[3] 胡程，邹志云，梅亚南，等. 城市道路网规划评价指标体系研究[J]. 土木工程与管理学报，2006（S2）：98-101.

[4] 李俊芳，吴小萍. 基于AHP-FUZZY多层次评判的城市轨道交通线网规划方案综合评价[J]. 武汉理工大学学报：交通科学与工程版，2007（02）：205-208.

[5] 胡寿松，何亚群. 粗糙决策理论与应用[M]. 北京：北京航空航天大学出版社，2006.

[6] 张明. 粗糙集理论中的知识获取与约简方法的研究[D].南京：南京理工大学，2012.

[7] 张文修，吴伟志，梁吉业，等. 粗糙集理论与方法[M].北京：科学出版社，2001.