基于SolidWorks API的异向双螺杆的参数化设计

陈 龙，董力群，张亚军，范一强

(北京化工大学机电工程学院，北京 100029)

0 前言

双螺杆挤出机是聚合物加工的主要设备之一，按照2根螺杆的旋转方向分类，可分为同向旋转双螺杆挤出机和异向旋转双螺杆挤出机。按照一根螺杆相对于另一根螺杆的位置，可分为啮合型双螺杆挤出机和非啮合型双螺杆挤出机。啮合异向双螺杆挤出机广泛用于塑料的挤出成型和造粒。啮合异向双螺杆一根螺杆的螺棱插入另一根螺杆的螺槽中，使连续的螺槽被分为相互隔离的C形小室，纵横向封闭性好，正位移输送能力强，物料无法滞留在螺杆表面，因而具有优异的自洁性能。学者对啮合异向双螺杆的设计和研究都需要进行三维实体造型，完成这一过程需要对异向双螺杆几何学具有比较深入的了解，并且三维实体造型需要花费很多时间成本，尤其是对异向双螺杆进行有限元模拟来确定合理的螺杆参数时，需要进行大量的三维实体造型，工作繁琐，效率低下。从国内的现阶段的情况看，对异向双螺杆的参数化设计鲜有研究。

SolidWorks提供了应用程序编程接口API(Application Programming Interface)，允许用户使用支持OLE或COM的编程语言(C++、Visual Basic、Delphi 等)，通过API调用SolidWorks界面中所有操作等效于使用用户接口进行的操作，来实现自动化设计工作，创建运行在SolidWorks程序进程内或进程外的工程应用程序，实现二次开发，使重复性工作简单化自动化，极大地提高了效率[1]。

Visual Basic(VB)是运行在Windows环境下的一种可视化编程语言，使用面向对象的编程方法(OOP)，它所具有的图形设计工具、结构化的事件驱动编程模式和开放的环境，可以使用户即快又方便地编写出Windows下的应用程序。在SolidWorks中通过宏录制可以记录SolidWorks用户的整个产品设计过程，把用户的界面菜单操作所用到的SolidWorks对象、方法都一一记录下来，其语法完全符合Visual Basic[2-3]。

1 异向双螺杆端面曲线形成及修正

1.1 全啮合异向双螺杆运动原理及端面曲线

异向双螺杆和同向双螺杆的运动原理是不同的，同向双螺杆假设一根螺杆固定不动，另一根螺杆绕不动螺杆作圆平动，而异向双螺杆假设一根螺杆固定不动，另一根螺杆绕不动螺杆的圆作相对纯滚动，螺杆B绕螺杆A顺时针旋转的同时，也绕着自己的中心顺时针旋转[4-5]。图1(a)所示为同向双螺杆相对运动原理，图1(b)所示为异向双螺杆相对运动原理。

根据相对运动原理可以推导出全啮合双头异向双螺杆的理论端面曲线，得到的理论端面曲线如图2所示。

推导出的全啮合双头异向双螺杆的理论端面曲线的8段圆弧方程[6]，分别是：

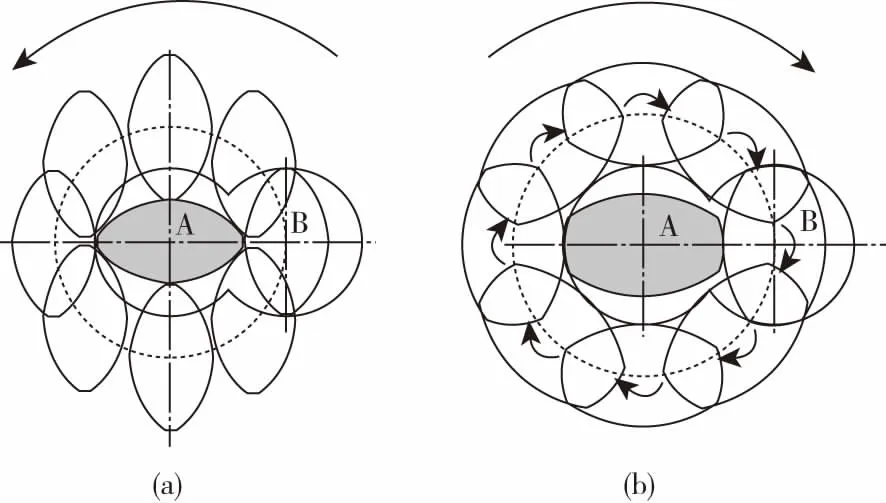
(a)同向双螺杆 (b)异向双螺杆图1 同向和异向双螺杆运动原理图Fig.1 Relative motion of co-rotating twin-screws and counter-rotating twin-screws

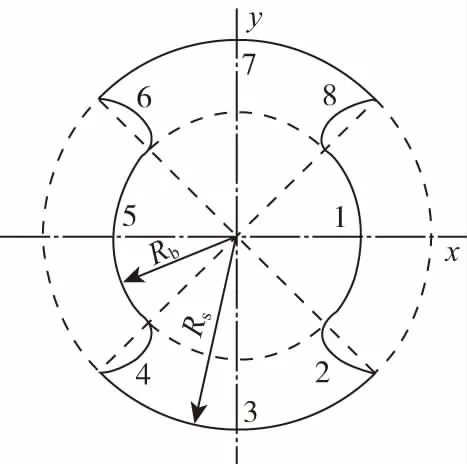
图2 全啮合异向旋转双头双螺杆理论端面曲线Fig.2 Theoretical end curve of intermeshing counter-rotating twin-screws

1、5段：

(1)

3、7段：

(2)

2段：

(3)

4段：

(4)

6段：

(5)

8段：

(6)

式中Rb——螺杆根圆半径,mm

Rs——螺杆顶圆半径,mm

CL——全啮合时两螺杆的中心距, mm,CL=Rb+Rs

ω——螺杆旋转的角速度，rad/s

t——螺杆旋转的时间,s

1.2 端面曲线的修正

通过三维软件螺旋扫描端面曲线即可得到全啮合异向双螺杆三维实体。在实际应用中，如果依照理论曲线加工，螺杆之间完全没有间隙，但是在实际螺杆加工实现无间隙不仅对于加工刀具和工艺要求非常高，而且由于热胀冷缩两螺杆很容易干涉，存在很大的安全隐患，同时在螺杆的根部很容易形成积料和死角。因此实际应用中通常对理论曲线进行修正，使两螺杆螺棱侧面之间有一定侧间隙。

实际异向双螺杆通常把理论端面曲线第2、4、6、8段改用直线，最简单的方法是直接相连，如图3(b)所示。这样螺杆之间依旧没有间隙且会发生干涉[7]。为了使两啮合螺杆间存在侧间隙，将直线向内偏移一个β角，如图3(c)所示，使螺棱宽度小于螺槽宽度，从而得到既有侧间隙又不会干涉的异向双螺杆端面曲线。如图4所示为修正后的异向双螺杆端面曲线。图中Rb为螺杆根圆半径；Rs为螺杆顶圆半径，槽深H等于顶圆半径减去根圆半径；α为螺槽角，其和导程T决定螺槽的宽度w；θ为螺棱角，其和导程T决定螺棱的宽度e，e应小于w，所以θ应小于α；β为摆动角，决定螺棱螺槽的断面形状和螺杆螺棱侧面之间的侧间隙δs。当β1=β2=0时，断面形状为矩形，如图5(a)所示；当β1≠0β2≠0时，断面形状为梯形，如图5(b)所示；当β1=0β2≠0或β1≠0β2=0时，断面形状为锯齿形，如图5(c)所示。各参数之间具体关系如式(7)～(8)所示。

(7)

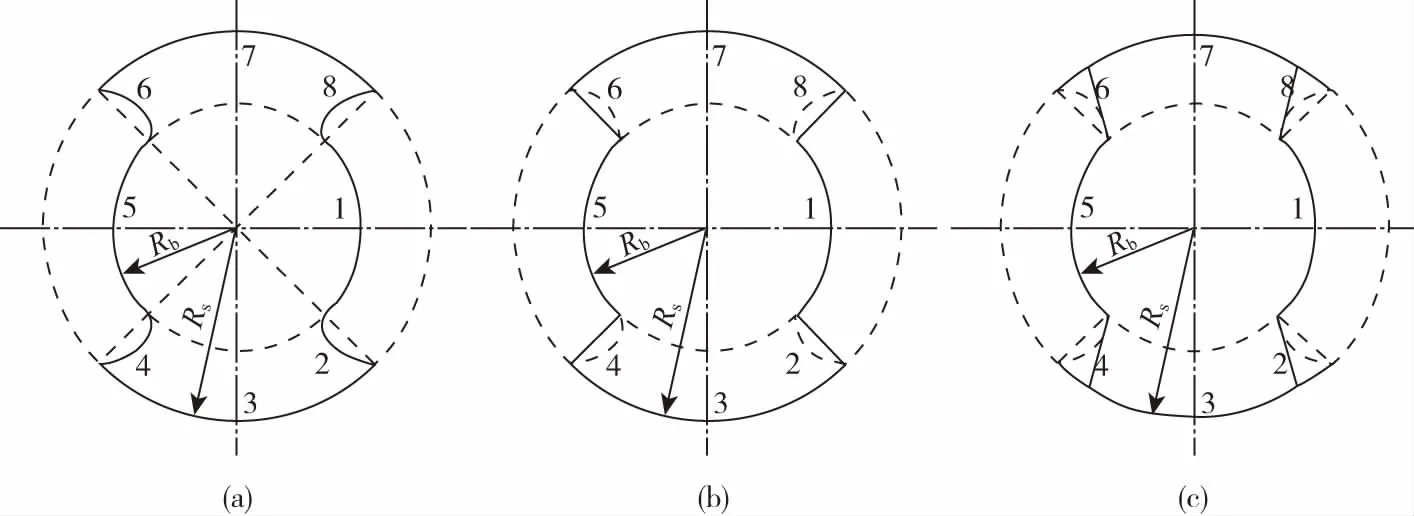
(a)理论端面曲线 (b)初步修正端面曲线 (c)最终修正端面曲线图3 异向双螺杆端面曲线的修正Fig.3 Correction of the end curve of counter-rotating twin-screws

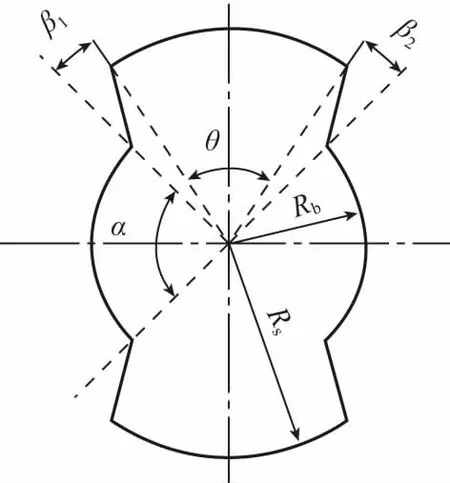
图4 修正后的异向双螺杆端面曲线Fig.4 The end curve of counter-rotating twin-screws after correction

(a)矩形 (b)梯形 (c)锯齿形图5 螺棱、螺槽断面形状Fig.5 The section shape of screw flight and groove

(8)

2 异向双螺杆的参数化设计

2.1 参数化设计流程

(1)录制宏，通过用户接口手动建立异向双头螺杆的三维模型。SolidWorks宏可以记录SolidWorks用户接口执行的各种操作，并且可以重放这一过程。宏录制前需要规划好异向双螺杆三维实体造型的步骤，录制时尽量减少视图变换次数和其他不必要的操作，录制后需要对其进行测试，看是否可以重放三维实体造型这一过程。

(2)录制完宏后，需要编辑宏代码，这个过程主要是理解和整理代码。找出宏代码中与异向双螺杆三维模型生成的关键函数，理解函数中各参数的意义。同时需要对宏代码进行整理，删除不需要的调用和代码，对代码进行注释来说明各参数的实际意义和各代码的功能。

(3)编辑完宏代码后，需要向宏中添加用户窗体。向窗体中添加标签、文字框、命令按钮等控件，并合理设计布置其位置。模块中只需要添加显示用户窗体的代码。将代码从模块转移到按钮事件，并根据不同功能的按钮修改代码，定义变量来替换代码函数中需要自定义的参数，这样就完成了螺杆的参数化设计。

(4)最后调试程序代码。一步步运行代码，检查程序是否正确运行，使用各种实例来验证程序。

2.2 程序操作流程和实例

基于Visual Basic 的可视化编程创建了异向双螺杆三维造型的程序界面，如图6所示。在操作界面中展示了带参数化尺寸的异向双螺杆端面曲线，方便用户快速理解和准确输入各个尺寸。程序具体的操作流程为：

(1)在程序对应的参数栏中输入需要的尺寸；

(2)分别点击左旋和右旋按钮，激活SolidWorks自动建立用户自定义尺寸的三维异向双螺杆左旋和右旋模型；

(3)点击退出按钮，退出程序，完成模型的建立和保存。

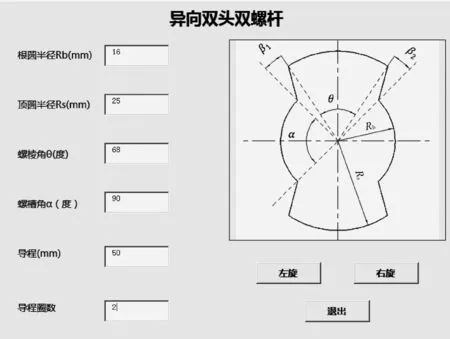
图6 程序界面Fig.6 Program interface

利用该程序可以建立不同直径、导程、长度和螺棱、螺槽断面形状的异向双头双螺杆的三维模型。如图7所示，是利用该程序建立的不同螺棱、螺槽断面形状的螺杆三维模型。图7(a)断面形状为梯形，所用参数：根圆半径16 mm，顶圆半径25 mm，螺棱角68 °，螺槽角90 °，导程50 mm，圈数2。图7(b)断面形状为矩形，所用参数：根圆半径16 mm，顶圆半径25 mm，螺棱角80 °，螺槽角100 °，导程50 mm，圈数2。如图8所示，是生产实践中常用的异向螺杆构型。利用该程序建立的五段螺杆组合而成的整段螺杆构型，从右到左分别为加料段、压缩段、密封段、排气段和计量段，这5段双螺杆因功能的不同而具有不同导程和长度，但是都可以很方便地用程序建立出来。

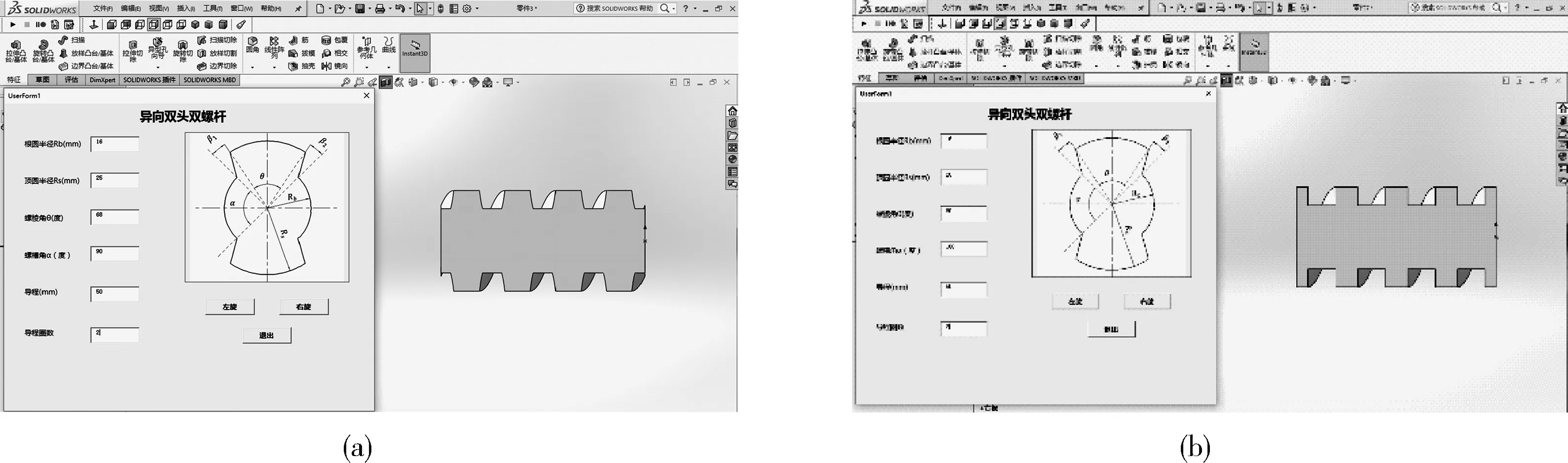
(a)梯形 (b)矩形图7 梯形和矩形断面形状螺杆三维模型Fig.7 3D model of trapezoidal and rectangular cross-section shape screws

图8 异向双螺杆三维模型Fig.8 3D model of counter-rotating twin-screws

3 结论

(1)研究了异向双头双螺杆端面曲线的形成原理及其修正方法，阐明了端面曲线螺棱螺槽角和三维模型螺棱螺槽宽度以及侧间隙之间的关系;

(2)以三维建模软件SolidWorks为软件平台，以SolidWorks API函数接口为基础，编写了异向双头双螺杆三维参数化程序算法，设计了异向双头双螺杆参数化程序界面,能满足不同直径、导程、长度和螺棱、螺槽断面形状的异向双头双螺杆三维模型自动生成,极大提高了异向双头双螺杆的设计效率和设计精度，为进一步的有限元分析和计算机模拟奠定了基础。

[1] 彭 鹏，邓 梅，陆 慧. 基于SolidWorks 的钣金参数化设计制图二次开发[J]. 现代机械, 2017, 44(2): 70-74.

PENG P，DENG M，LU H. Secondary Development of Parametric Design and Drawing of Sheet Metal Based on SolidWorks[J]. Modern Machinery, 2017,44(2): 70-74.

[2] 马咏梅，丁行武，李 鑫. SolidWorks二次开发在机械零件设计中的应用与研究[J]. 机械传动, 2010, 34(1): 72-74.

MA Y M，DING X W，LI X. The Research and Application of Further Development of SolidWorks in Design of Machine Parts[J]. Journal of Mechanical Transmission, 2010, 34(1): 72-74.

[3] 谢征恒，王生泽. 基于SolidWorks API的椭圆齿轮参数化设计及加工仿真[J]. 东华大学学报(自然科学版), 2009, 35(4): 467-471.

XIE Z H，WANG S Z. Parametrical Design and Machining Simulation of Elliptical Gear Based on SolidWorks API[J]. Journal of Donghua University(Natural Science), 2009, 35(4): 467-471.

[4] BOOY M L. Geometry of Fully Wiped Twin-screw Equipment[J]. Polymer Engineering & Science, 1978, 18(12): 973-984.

[5] RAUWENDAAL C. The Geometry of Self-cleaning Twin-screw Extruders[J]. Advances in Polymer Technology, 1996, 15(2): 127-133.

[6] 耿孝正. 双螺杆挤出机及其应用[M].北京：中国轻工业出版社, 2003:58.

[7] 宋俊全，冯连勋. 啮合导向旋转双螺杆三维实体造型研究[J]. 中国塑料, 2003, 17(3): 92-96.

SONG J Q，FENG L X. Research on 3D Solid Modeling for the Intermeshing Counter-rotating Twin-screw[J]. China Plastics, 2003, 17(3): 92-96.