管内封堵器胶筒硬度对其自密封特性影响研究

，仕民，

( 中国石油大学(北京) 机械与储运工程学院，北京 102249)①

管道是输送原油及天然气的主要方式，由于其复杂的运行环境，经过长时间运行之后难避出现如裂纹、腐蚀、凹陷等事故。为了避免或减少由此造成的经济损失，管道维抢修技术近年来得到了越来越广泛的应用。管内智能封堵技术[1-3]作为一种新型的管内封堵技术，是管道，特别是海洋管道的维抢修的先进技术。

管内智能封堵技术的核心装备是管内智能封堵器，其可以实现在管内指定位置的锚定与封堵[4-5]，如图1所示。管内封堵主要是靠挤压胶筒使其与管壁形成接触密封力，所以胶筒的密封性能将直接影响管内智能封堵器的性能。

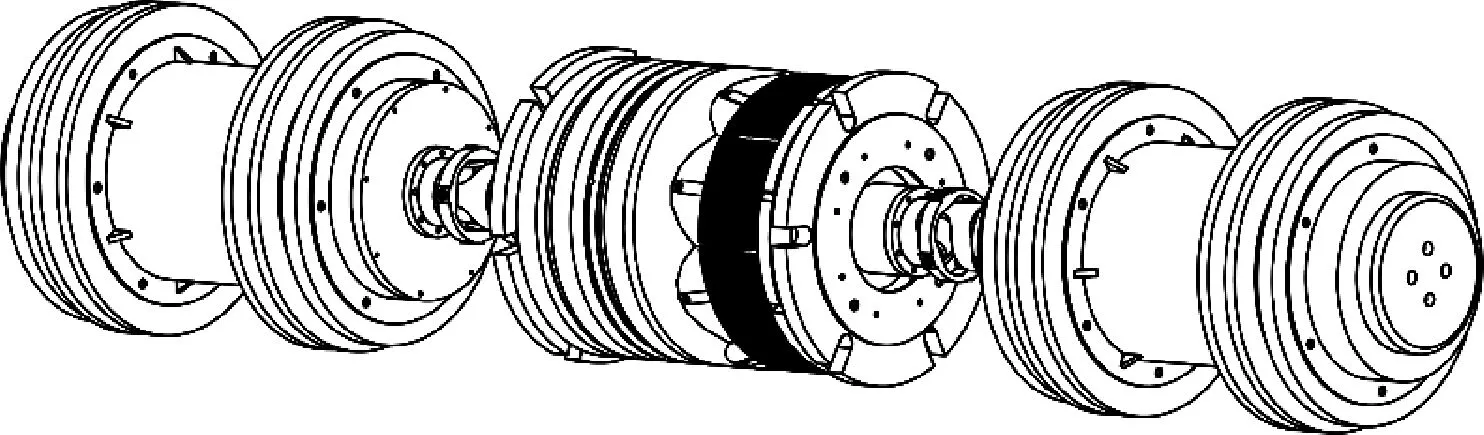
图1 管内智能封堵器示意

对于胶筒的密封研究已经比较广泛，胶筒结构及形状的优化研究已有很多[6-9]。胶筒的另外一个非常关键的参数是自密封，胶筒的自密封在整个密封过程中起到非常重要的作用。本文通过模拟的方法，对胶筒的密封性能以及胶筒硬度对自密封性能的影响进行研究。

1 胶筒自密封特性

管内智能封堵器胶筒的工作过程类似于封隔器的胶筒，密封过程如图2所示。封堵过程主要通过液压缸带动挤压环移动，逐渐挤压胶筒，使其轴向受挤压，产生径向膨胀，并与管壁形成接触应力，进而形成管内密封。

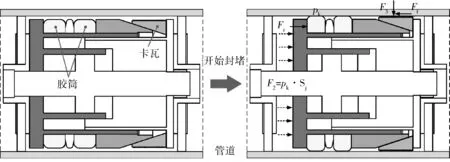
图2 封堵器封堵过程示意

假设胶筒与管壁之间形成的接触压力等于胶筒在管内可以封堵的管内压差。在胶筒密封过程中，首先液压缸挤压胶筒，使之膨胀与管壁形成初始密封，产生初始接触压力，这一过程挤压胶筒所需的推力为FZ；形成接触压力后，由前后压差pk在封堵器端面产生的轴向力为F2。在初始阶段，由于接触压力较小，FZ>F2；随着接触压力逐渐增大，当达到某一时刻后，FZ≤F2，这时胶筒继续挤压所需的推力由管内压差产生的轴向力提供，此时胶筒可以实现越压越紧，即实现自密封。实现自密封的条件为

(1)

2 胶筒密封性能模拟分析

2.1 模型选择

在保证计算准确性的前提下，为使计算更加快速，对模型进行了适当简化，简化后的模型如图3所示。主要由胶筒、底座、推环以及管道组成。胶筒模拟模型采用轴对称模型，胶筒的特性选用Mooney-Rivlin本构模型。

图3 模拟模型

模型所选的参数与工程中实际参数相同，如表1所示。

表1 模型选取参数 mm

对于Mooney-Rivlin本构模型，其应变能密度函数的表达式为

(2)

式中：W为应变势能；I1、I2为变形张量；C10、C01为Mooney-Rivlin常数。

工程应用中拉压变形不超过25%、剪切变形不超过75%的变形称为橡胶小变形，其泊松比μ、弹性模量E、剪切模量G和材料系数的关系为

(3)

由于橡胶材料形状的可变性，泊松比μ=0.5时，G和E与C10和C01的关系为[10]

(4)

根据式(4)可以求出胶筒弹性模量(硬度)与模型常数之间的关系，进而对不同硬度的胶筒进行模拟分析。

2.2 网格划分及边界条件

在进行网格划分时，胶筒由于会发生非线性的大变形，所以其网格类型设置为CAX4RH，其余零件的设置无需更改。模型网格设置如图4所示。

图4 模型网格划分

模型的边界条件的设置由实际工作状态的边界条件来设置，如图5所示。底座的边界设置为完全固定；管道的外径边界设置为完全固定；推环的上边界设置为只沿y轴平动；其余均设置为自由边界条件。

图5 模型边界条件设置

2.3 自密封性能分析

为了验证自密封性能，选取如表1的模型参数进行分析，胶筒的硬度选取70 HS。在600 kN轴向挤压力作用下胶筒变形如图6所示。

图6 挤压力为600 kN时的模拟结果

在不同轴向挤压力作用下的胶筒变形及与管壁形成的接触应力，对其进行了自密封分析，如图7所示。

从图7可以看出，当胶筒与管壁的接触压力处于交点M点以下时，由管内压差所提供的轴向力始终小于挤压胶筒所需的轴向力，在此阶段胶筒不能形成自密封；随着挤压轴向力逐渐增大，胶筒与管壁之间的接触压力也逐渐增大，当接触压力增大到交点M点以上后，由管内压差所提供的轴向力将始终大于挤压胶筒所需的轴向力，换言之，此时由管内压差所提供的轴向力完全可以使胶筒形成可靠密封而不产生泄露，即胶筒可以形成自密封。

图7 管内压差提供的轴向力与挤压胶筒所需轴向力的对比曲线

M点处，胶筒与管壁之间的接触压力为pk=2.02 MPa，所需的轴向挤压力为FZ=340 kN。即液压缸只需提供340 kN的轴向力挤压胶筒，使之膨胀与管壁形成2.02 MPa的接触压力后，胶筒就可以形成自密封。

3 胶筒硬度对自密封性能的影响

在实际工程应用中，对于胶筒的选择要考虑很多因素，例如最大密封压力、所需轴向挤压力、抗剪切强度等；胶筒的自密封性能也是胶筒设计中的关键性能参数。胶筒的硬度会对胶筒的自密封性能产生影响，硬度不同自密封能力也不同，因此需要研究胶筒的硬度对其自密封性能的影响，探究胶筒的硬度最优值，为胶筒的设计及工程应用提供指导。

胶筒硬度选择50～80 HS，分别计算不同硬度下胶筒与管壁之间的接触应力与所受轴向挤压力之间的关系，进而分析胶筒硬度对其自密封性能的影响。不同硬度下胶筒的自密封性能的影响曲线如图8所示。

由图8可以看出，随着胶筒硬度不断增大，各条曲线的斜率几乎相等，而曲线的截距不同。胶筒的硬度越大，截距越大；各条曲线与压差提供的轴向力曲线的交点的值也就越大。说明随着胶筒硬度的增加，需要提供更大的轴向压缩力使胶筒形成自密封。这一特性也可以通过胶筒密封的理论力学分析来解释。

图8 不同胶筒硬度对自密封性能的影响曲线

由理论推导的压缩式密封胶筒的力学性能分析式为[11]

由式(5)可以得出，曲线的截距与胶筒的弹性模量成正比，即应该与胶筒的硬度成正比。图9为产生2 MPa接触应力时不同硬度胶筒所需的轴向压缩力。

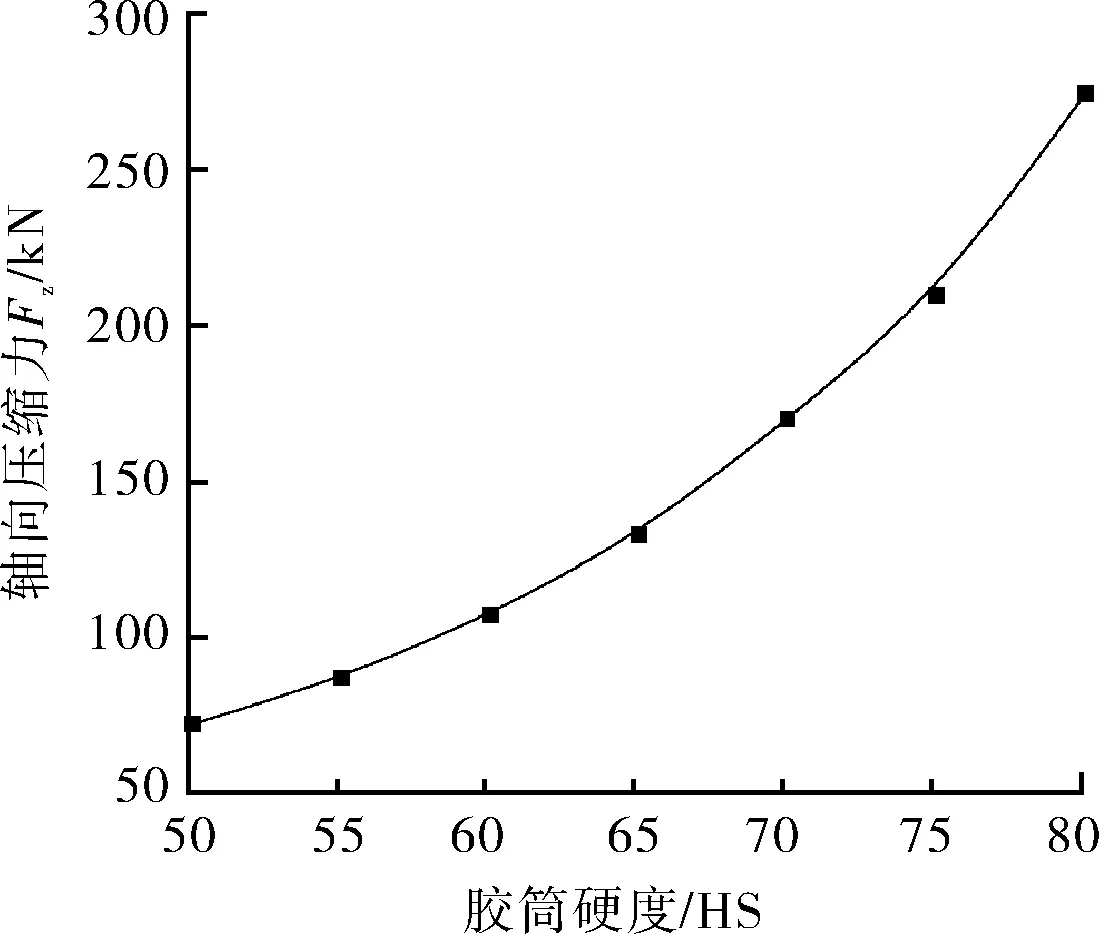
图9 产生2 MPa接触应力时不同硬度胶筒所需的轴向压缩力

从图9中可以看出，当胶筒与管壁形成2 MPa的接触应力时，所需轴向压缩力的变化与胶筒的硬度不是正比关系，而是近似二次曲线关系。产生这种现象的原因是由于在胶筒的压缩变形过程中会与底座及管壁产生摩擦力，此摩擦力很难精准预测及计算，而且随着胶筒硬度的增大，产生的摩擦力也越大；在形成相同的接触应力的情况下，所需要的轴向压缩力也就越大。

4 结论

1) 胶筒的自密封特性是胶筒研究的关键问题之一。管内封堵器的胶筒在密封过程中可利用其自密封特性，只需提供一定的轴向挤压力，使胶筒与管壁形成足够的接触应力，在密封压差的作用下胶筒可以完成封堵而无需再继续施加轴向力。

2) 胶筒的硬度对胶筒的自密封特性存在一定的影响，无论从理论分析还是从模拟分析中都可以得出，随着胶筒硬度的增加，完成一定密封时所需的轴向压缩力也越大，而且胶筒越硬，其形成自密封所需要达到的初始接触应力越大。从这一角度来看，选择的胶筒硬度越软越好，但在实际工程应用中对于胶筒的选择还需要结合其他参数指标来综合评定。

3) 本文的研究结果不但对管内封堵器胶筒的参数设计提供了理论基础，而且对该技术的应用具有一定的指导作用。

[1] Aleksandersen J， Tveit E. The smart plug：A remotely controlled pipeline isolation system [C]// The Eleventh International Offshore and Polar Engineering Conference， 2001.

[2] 张康，张仕民，朱霄霄，等. 基于管内智能封堵技术的新型管道维修技术[J]. 石油机械， 2017， 45 (1)：114-119.

[3] 张仕民，梅旭涛，王国超，等. 油气管道维抢修方法及技术进展[J]. 油气储运， 2014， 33 (11)：1180-1186.

[4] 王焱，张仕民，张行，等.φ1 016 mm油气管道管内智能封堵器的设计[J]. 管道技术与设备， 2015 (1)：27-29.

[5] 耿岱，张仕民，王德国，等. 管道智能封堵器锚爪结构的优化[J]. 油气储运， 2011， 30 (4)：279-282.

[6] 王晓，孔学云，王俊姬，等. 压裂封隔器胶筒研制及密封性能模拟试验分析[J]. 石油矿场机械， 2015， 44 (4)：74-80.

[7] 张辛，徐兴平，王雷. 封隔器胶筒结构改进及优势分析[J]. 石油矿场机械， 2013， 42 (1)：62-66.

[8] 马卫国，张亚昌，张德彪，等. 双胶筒封隔器胶筒密封性能分析[J]. 石油机械， 2010， 38 (11)：51-53.

[9] 张宝岭，王西录，徐兴平. 高压封隔器密封胶筒的改进[J]. 石油矿场机械， 2009， 38 (1)：85-87.

[10] 郑明军，王文静，陈政南，等. 橡胶Mooney-Rivlin模型力学性能常数的确定[J]. 橡胶工业， 2003 (8)：462-465.

[11] 仝少凯. 压缩式封隔器胶筒力学性能分析[J]. 石油矿场机械， 2012， 41 (12)：1-7.