基于Hadoop的Lorenz超混沌加密算法设计
2018-03-29温贺平鲍晶晶柯居鑫刘树威
温贺平,鲍晶晶,柯居鑫,刘树威
(1.东莞职业技术学院信息与教育技术中心,广东 东莞 523808; 2.东莞职业技术学院电子工程系,广东 东莞 523808)
0 引 言
随着移动互联网、云计算等新兴信息技术的飞速发展,人类已经进入了大数据时代。当前,用户数据的安全与隐私保护无疑成为大数据环境中最为重要的问题之一[1-2]。Hadoop作为当今大数据处理平台的主流架构之一,其数据安全问题引起了广泛的关注[3-4]。
针对云计算和大数据环境中的数据安全问题,基于Hadoop的数据加密保护成为当今研究的一个热点课题[5-7]。文献[5]提出了一种适合云存储的线性AES-ECC混合加密算法,算法综合了AES适应于大块数据加密且加解密速度快和ECC加密强度高的特点,使用交叉加密的方式,极大地提高了云存储的安全性。文献[6]结合Hadoop分布式计算框架提出了一种DES和AES混合的加密改进算法,该算法通过对明文划分进行混合加密,并且加入随机扰动信息,有效地提高了安全性。文献[7]结合云环境的并行计算特点和AES加密算法,设计了一种并行AES加密方案,利用MapReduce并行编程架构,加密方案具有更高的加密效率。然而,目前这方面的研究工作主要是基于传统加密算法进行的,随着量子计算机技术的发展,传统加密算法如DES和AES等将面临巨大挑战[8]。混沌是确定性系统中的内秉随机运动,具有对初始状态及控制参数的高度敏感性、良好的伪随机性、遍历性、不可预测性等特征,与密码学中的混淆、扩散、密钥等存在许多相似之处[9]。近些年来,混沌密码学引起了各个领域研究者的密切关注[10-12]。
因此,在大数据环境中研究和设计高效、安全的混沌密码算法具有重要的理论意义和应用价值。本文提出一种基于Hadoop的超混沌加密算法。1)利用Lorenz超混沌系统更加复杂的动力学行为特点,产生4个状态变量的混沌序列。2)对各变量的混沌序列采用混合异或的方法产生具有更好密码特性的混沌序列。3)结合Hadoop平台的MapReduce并行编程模型,设计兼具较高执行效率和安全性的密码算法。
1 Hadoop大数据处理平台
Hadoop是Apache基金会的一个开源分布式框架。Hadoop具有容错性高、扩展性强等特点,适合海量数据离线批处理的场合。Hadoop包括HDFS和MapReduce这2个核心组件[13-15],其中HDFS实现分布式存储,MapReduce实现分布式计算。
1.1 HDFS
HDFS分布式文件系统,即Hadoop Distributed File System。HDFS采用了主从(Master/Slave)结构模型,一个HDFS集群是由一个NameNode和若干个DataNode组成的。其中NameNode作为主服务器,管理文件系统的命名空间和客户端对文件的访问操作,而集群中的DataNode管理存储数据。
1.2 MapReduce
MapReduce是一种编程模型,用于大规模数据集的并行运算。一个MapReduce作业(job)通常会把输入的数据集切分为若干个独立的数据块,由map任务(task)以完全并行的方式处理它们。框架会对map的输出先进行排序,然后把结果输入给reduce任务。通常中间处理的结果会存储在本地磁盘,而作业的输入和输出都会被存储在HDFS中。
2 Chen超混沌系统
超混沌系统是指具有2个或2个以上正Lyapunov指数的混沌系统,超混沌系统的相轨迹可以在更多方向上进行拉伸和折叠运动,其动力学行为比一般的混沌系统更为复杂[16]。Lorenz混沌系统方程组为:
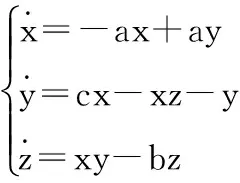
(1)
其中,x,y,z是状态变量,当系统参数取值为a=10,b=8/3,c=28时,系统处于混沌态,混沌吸引子相如图1(a)所示。
Lorenz超混沌系统[17]方程组为:
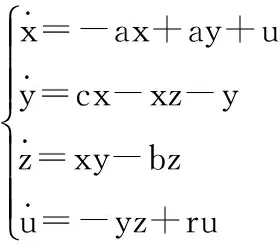
(2)
其中,x,y,z,u是状态变量,当系统参数取值为a=10,b=8/3,c=28,d∈(-1.52,-0.06]时,系统处于超混沌态,d=-1超混沌吸引子相如图1(b)所示。
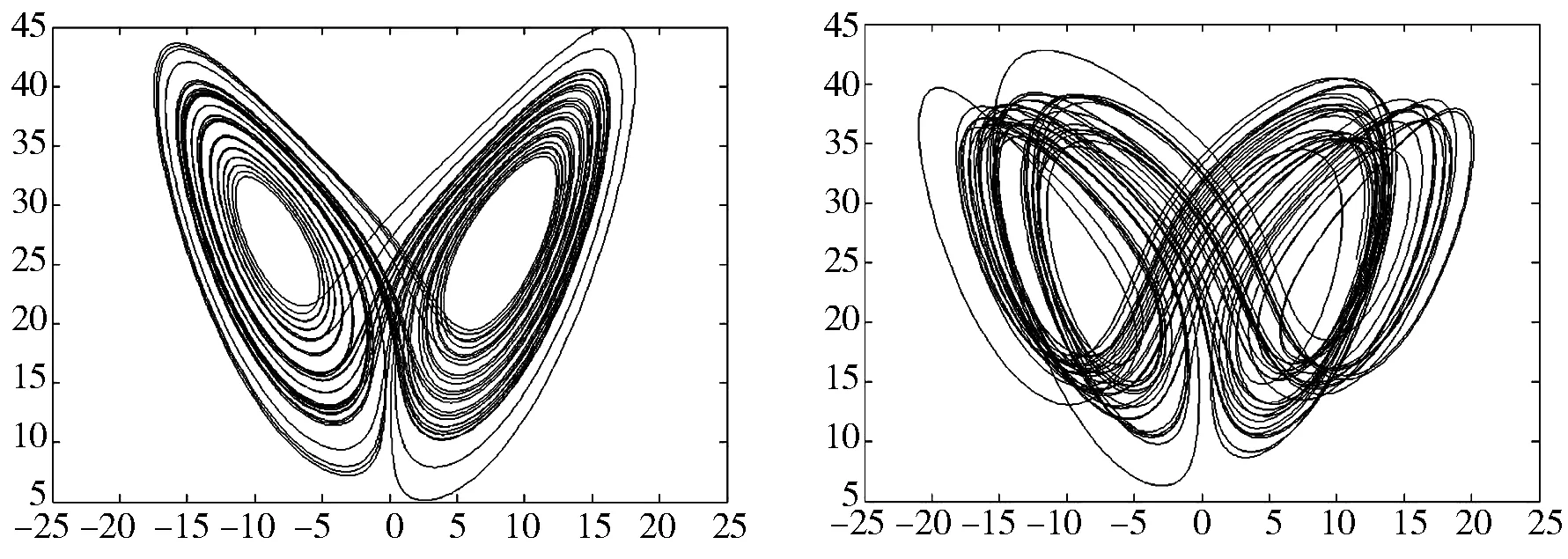
(a) Lorenz混沌 (b) Lorenz超混沌图1 混沌吸引子相图
3 Hadoop下的超混沌密码算法
3.1 超混沌系统密码序列处理
混沌系统所产生的状态变量值不能直接应用于数据加密,为此需要将超混沌系统进行处理,以满足数据加密算法的需要。根据式(2),Lorenz超混沌系统可以同时产生4个混沌序列,超混沌系统处理步骤如下:
步骤1选取Lorenz超混沌的初值和系统参数作为加密密钥K(e)或解密密钥K(d),让系统开始迭代运行。为确保超混沌Lorenz系统完全进入混沌状态,预先让系统迭代l>50次,并丢弃前面l个迭代序列。
步骤2对Lorenz超混沌的无量纲状态方程通过四阶龙格库塔法作离散化处理,将连续的混沌系统状态变量转换为适合于数据加密的离散混沌序列。得到4个混沌序列分别表示为:x(k+l),y(k+l),z(k+l),u(k+l), k=1,2,…,n。
步骤3算法采用的加密方式为按照字节为单位按位异或流密码方式进行加密,因此将混沌序列处理为8位长度,取值为[0,255]的序列值。具体处理方法如下:
(3)
其中,mod为模取余数运算,⎣」为向下取整运算,px(k),py(k),pz(k),pu(k)为经过预处理后的4个离散混沌序列。
步骤4为进一步增强混沌序列的随机特性,将式(3)产生的混沌序列进行混合异或运算操作,得到用于数据加密和解密算法的混沌序列。
(4)
其中,⊕表示按位异或运算,p(e)(k)为Lorenz超混沌系统采用加密密钥K(e)所产生的用于数据加密的混沌序列,p(d)(k)为采用解密密钥K(d)所产生的用于数据解密的混沌序列。
3.2 基于Hadoop的密码算法设计
在Hadoop平台上,首先将存储在HDFS上的大数据文件或大数据集进行分片处理,接着通过MapReduce并行编程模型的Map函数实现并行加密和解密操作,最后利用Reduce函数完成数据或数据集的归并,最终存储在HDFS上。基于Hadoop的超混沌加密算法总体框架如图2所示。数据加密算法设计具体步骤如下:

图2 基于Hadoop的超混沌加密算法总体框图
步骤1读取存储在HDFS上数据,并进行分片处理,为MapReduce并行处理做准备。
步骤2Map函数以键值对形式读取经过分片处理的数据块进行并行加密。Map函数的输入键值对以

(5)
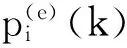
步骤3Reduce函数对加密后的数据块或数据集进行归并。Reduce函数的输入键值对以
步骤4将经过Reduce函数归并后的结果存储在HDFS上,完成数据加密的过程。
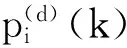

(6)
4 实验结果分析
4.1 Hadoop实验环境
Hadoop实验环境的硬件采用一台高性能物理服务器上搭建若干个虚拟机进行实现。硬件服务器配置:CPU Intel(R) Xeon E3-1225 v3, 3.2 GHz/8 MB Cache,内存16 GB,磁盘1 TB,千兆以太网卡。软件配置:虚拟机软件VMware Workstation 12,单个虚拟机的配置为单核CPU和1 GB内存,Linux系统是CentOS-7.16,Hadoop版本为Hadoop 2.7.3,Java版本为Jdk8,IDE开发环境为Eclipse3.8。
为了对比分析分布式并行加密的执行效率,实验利用虚拟机软件部署1~8个集群Slave节点数。根据图2所设计的算法,实验数据集选取2个大小分别为1 GB和2 GB的大数据文本文件,分别采用AES加密算法和本文所提的超混沌加密算法对大数据文本文件进行加密,进而对实验结果进行比较和分析。其中,Map分块数大小按照默认设置为dfs.block.size=128 MB。
4.2 数据加密效率分析
以1 GB的文本文件为例,当集群Slave个数为1时,被切分的8个Map数据块加密操作均在一台虚拟机上运行,属于单机运行模式。随着Slave节点数的增加,Map数据块加密的并行度增大。当Slave节点数为8时,Map数据块分别在8台虚拟机上并行地执行加密操作。在同等实验条件下,采用本文算法与AES算法执行效率比较情况如图3所示。实验结果表明,本文算法具有比AES算法更高的执行效率,根据统计结果可知,本文算法的执行效率提高了将近40%。
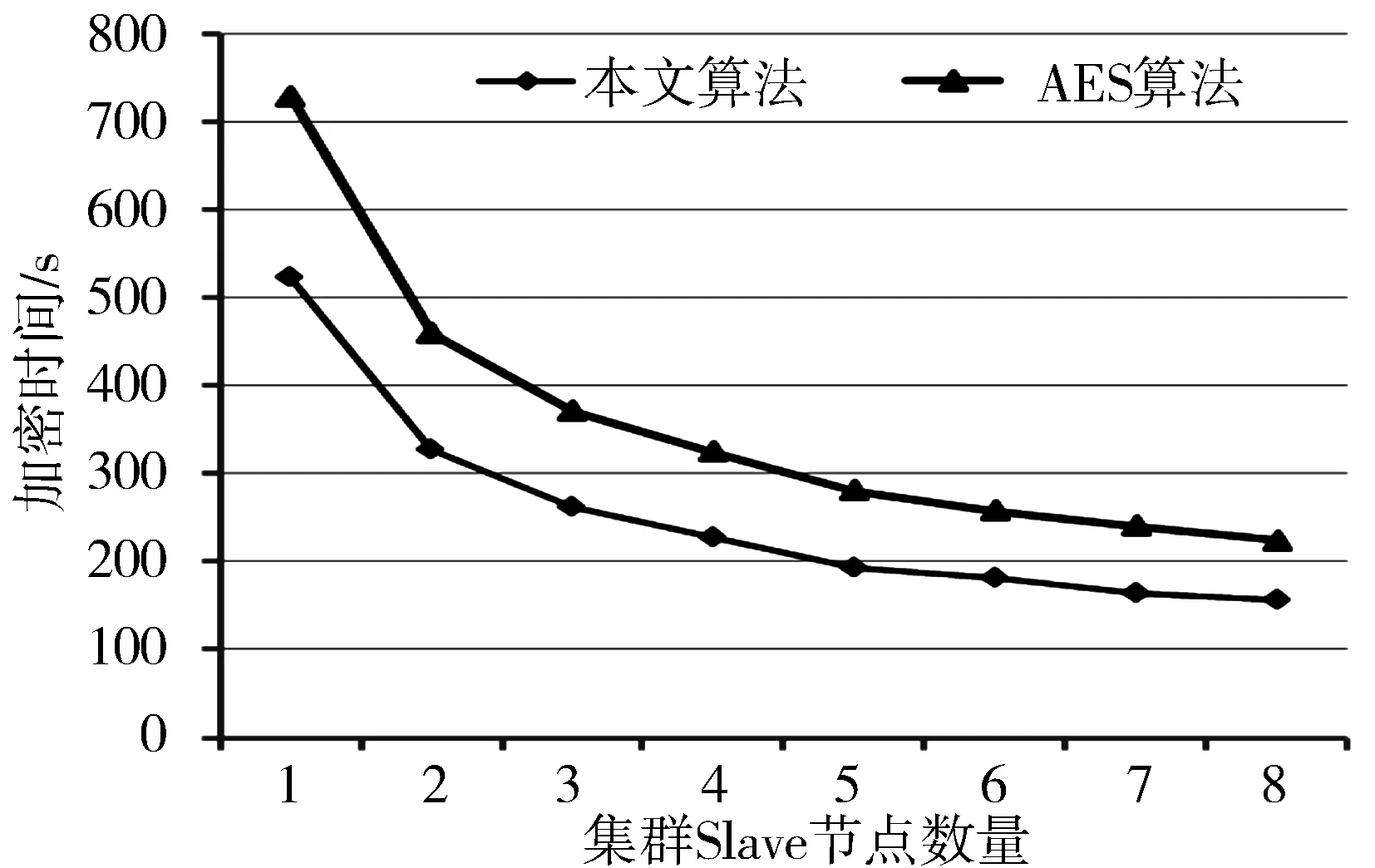
图3 本文算法与AES算法效率比较图
4.3 算法安全性分析
4.3.1 密钥空间
Lorenz超混沌系统具有对初始条件和参数的高度敏感性,算法选取系统的初始条件和超混沌控制参数作为加密和解密的密钥。密钥空间S∈{x0,y0,z0,u0,d},其中,x0,y0,z0,u0为系统初始条件,d为确保Lorenz混沌系统处于超混沌态的控制参数。选取初值和控制参数2类不同性质的密钥,在保证系统超混沌特性的同时,也在一定程度上提高了系统的安全性。密钥参数均选取双精度数据类型,精度为10-16,密钥空间大小为1016×5=80≈2265。AES的密钥长度可以为16,24或32 Byte(即128,192或256 bit)。因此,本文算法的265 bit密钥长度,大于AES算法最大的256 bit密钥长度,足以抵御暴力攻击。
4.3.2 密钥敏感性分析
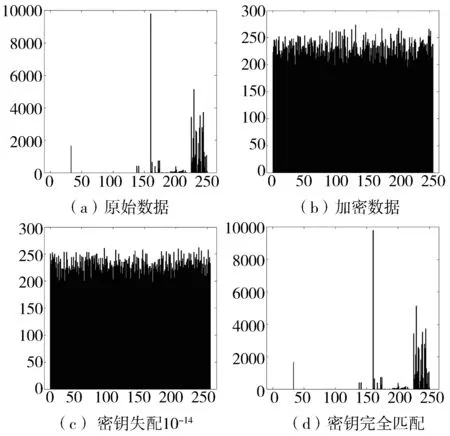
图4 数据加密和解密统计直方图
经过超混沌加密后的数据直方图呈现类噪声的随机分布状态,如图4(a)和图4(b)所示。算法对密钥参数具有高度敏感性,当密钥失配10-14时,文本直方图如图4(c)所示,当密钥完全匹配时,文本直方图如图4(d)所示。实验验证了算法具有良好的密文统计特性及密钥敏感性。
5 结束语
针对大数据数据安全问题,利用Lorenz超混沌系统更加复杂的动力学行为以及所产生的序列具有更好的随机性等特点,结合Hadoop平台的MapReduce分布式并行编程模型,设计了一种基于超混沌系统的并行加密算法。实验结果表明,相比于AES算法,本文设计的算法执行效率提高了将近40%。在安全性方面,算法具有密钥空间大、密文统计特性及密钥敏感性良好的特性。算法具有安全、高效的特点,在网络大数据中的数据安全及隐私保护方面具有广阔的应用前景。
[1] 曹珍富,董晓蕾,周俊,等. 大数据安全与隐私保护研究进展[J]. 计算机研究与发展, 2016,53(10):2137-2151.
[2] 冯登国,张敏,李昊. 大数据安全与隐私保护[J]. 计算机学报, 2014,37(1):246-258.
[3] 李颖超. 基于Hadoop的云存储系统文件处理与安全研究[J]. 现代电子技术, 2016,39(21):112-115.
[4] 凃云杰,白杨. 基于Hadoop和双密钥的云计算数据安全存储策略设计[J]. 计算机测量与控制, 2014,22(8):2629-2631.
[5] 卢昱,王双,陈立云. 基于云存储的混合加密算法研究[J]. 计算机测量与控制, 2016,24(3):129-132.
[6] 战非,张少茹. 基于云计算的混合加密DAES算法研究[J]. 电子设计工程, 2017,25(3):185-189.
[7] 付雅丹,杨庚,胡持,等. 基于MapReduce的并行AES加密算法[J]. 计算机应用, 2015,35(11):3079-3082.
[8] 刘红军. 混沌理论在一次一密图像加密及保密通信系统中的应用研究[D]. 大连:大连理工大学, 2014.
[9] 廖晓峰. 混沌密码学原理及其应用[M]. 北京:科学出版社, 2009.
[10] 武相军,王春淋,阚海斌. 基于多分数阶混沌系统的彩色图像加密算法[J]. 计算机与现代化, 2013(11):1-7.
[11] 张帆. 基于Lorenz-Duffing复合混沌系统的彩色图像加密[J]. 微电子学与计算机, 2013,30(10):62-65.
[12] 官国荣,吴成茂,贾倩. 一种改进Lorenz混沌系统构造及其加密应用[J]. 小型微型计算机系统, 2015,36(4):830-835.
[13] 陆嘉恒. Hadoop实战[M]. 北京:机械工业出版社, 2012.
[14] 董西成. Hadoop技术内幕:深入解析MapReduce机构设计与实现原理[M]. 北京:机械工业出版社, 2013.
[15] 宋杰,孙宗哲,毛克明,等. MapReduce大数据处理平台与算法研究进展[J]. 软件学报, 2017,28(3):514-543.
[16] 李伊林. 基于超混沌系统的自适应图像加密算法[J]. 计算机与现代化, 2014(7):137-141.
[17] Wang Xingyuan, Wang Mingjun. A hyperchaos generated from Lorenz system[J]. Physica A Statistical Mechanics & Its Applications, 2008,387(14):3751-3758.
