零一膨胀二项混合回归模型的改进EM算法

吕敏红,闫奕荣,吴成晶

(1.西安航空学院理学院,陕西 西安 710077; 2.西安交通大学经济与金融学院,陕西 西安 710049)

0 引 言

在现实生活中，数据来源于单一总体的假设往往是不成立的，如果仍然用同一个模型对这些“非同质”的数据进行处理，就会造成数据的散度偏大。混合回归模型是指多个混合成分按照一定的比例进行混合而成的回归模型，这样就可以将具有混合分布的数据有效地模型化。近年来，各类混合模型在基因研究、金融和贸易等众多研究领域迅猛发展，对混合模型的研究受到了越来越多统计学者的重视。Tchetgen等人[1]对广义线性混合效应模型的诊断检验问题做了研究，Li等人[2]基于EM算法考虑了正态混合模型的假设检验问题，Zhu等人[3]基于似然估计的方法研究了混合模型的渐进理论，Lin等人[4]研究了偏斜正态分布下有限混合模型的参数估计问题，Xiang等人[5]研究了两成分泊松混合回归模型的影响诊断问题，陈家骅等人[6]研究了有限混合Von Mises模型的极大似然估计。

计数数据广泛存在于医疗、保险和金融等多个研究领域，最早这类数据通常会用泊松分布或二项分布等经典的分布进行模拟，但是在实际问题中，观测数据可能存在过多的0或1，这时如果还用经典分布就会造成数据散度偏大。例如在车险理赔问题中，由于本年度理赔的次数会影响到下年度的保险费用，所以一般在较小的事故发生时，车主都会自掏腰包进行维修，所以从保险公司获得的车辆发生交通事故次数的数据就会出现零观测值过多的情况，这时就需要考虑零膨胀回归模型。自从Cohen[7]第一次考虑了零膨胀数据，提出调整的泊松回归模型后，对具有零膨胀的计数数据已经有了很多研究，Lambert[8]正式提出了零膨胀泊松回归模型，Fahrmeir等人[9]对零膨胀的可加模型进行了研究，Ridout等人[10]对零膨胀回归的贝叶斯方法进行了深入的研究，Jansakul等人[11]研究了零膨胀模型的score检验问题，Melkersson等人[12]在对看牙医次数的数据进行研究时，提出了零一膨胀泊松分布，Wang等人[13]对零一膨胀分布的性质进行了研究。尽管目前对于混合回归模型和零一膨胀模型已经有了很多方面的研究，但仍有较大的探索空间，特别是零一膨胀的混合模型还未涉及。

本文首先对零一膨胀二项混合回归模型的参数建立了极大似然估计，然后由于传统的EM算法只能使得估计收敛到局部极值，所以本文提出了MCEM算法对EM算法进行改进，使得零一膨胀二项混合回归模型能够找到全局最优解。最后再通过一个模拟研究验证该算法的有效性。

1 混合回归模型

混合回归模型[4]是指一个回归模型是由几个混合成分按照一定比例混合而组成的。也就是说，混合回归模型是将因变量服从混合分布的情形进行模型化，从而对总体的“非同质性”进行描述。在实际中，混合成分的个数大多是有限的，把这类模型称之为有限混合回归模型，具体形式如下：

(1)

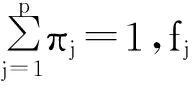
于是相应的对数似然函数为：

(2)

传统的极大似然估计是关于θ对式(2)求极大值，但是由于其结构比较复杂，直接求解是相当困难的。受数据添加思想的启示[13]，首先引入指示向量Wi=(wi1,wi2,…,wip)T，若yi来自第j个混合成分，记wij=1，否则wij=0。这样就有：

p(Wi=wi)=π1wi1π2wi2…πpwip

进一步可得：

这样基于完全数据的对数似然函数为：

(3)

2 零一膨胀二项混合回归模型

零一膨胀回归模型是计数数据中0和1都过多的计数模型，假设φ0表示数据中过多的0所占数据的比例，φ1表示过多的1所占的比例，而其他数据的取值服从某种离散分布，它们是按照一定的比例进行混合：

(4)

其中，f(y)表示来自某种离散分布，如二项分布、泊松分布等,φ2=1-φ0-φ1。

从式(4)可以看出数据集中的0来自2个部分，即第一部分的0和第三部分的0，1也是同样的道理来自2个部分。当φ1=0,φ2=0时，数据完全来自某种离散分布；当φ1=0,φ2≠0时，数据只在0处发生了膨胀，式(4)就简化为零膨胀模型。

如果式(4)中的某种离散分布为二项分布时，即f(y)～B(m,y)，模型便为零一膨胀二项分布(ZOIB),具体形式为：

(5)

其中，φ2=1-φ0-φ1，0来自非泊松分布中的0和二项分布中的0，1也是同样的道理。下面对模型(5)的参数部分引入协变量X和Z，这样便得到了ZOIB的具体形式：

(6)

其中，β和γ0,γ1是回归系数向量。

若式(1)中的每个混合成分都是ZOIB，则得到零一膨胀二项有限混合回归模型。特别地，当p=2时，则说明模型具有2个混合成分。本文重点研究具有2个混合成分的ZOIB混合回归模型，具体形式如下：

(7)

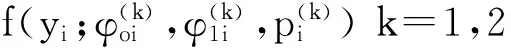
3 ZOIB有限混合回归模型的极大似然估计

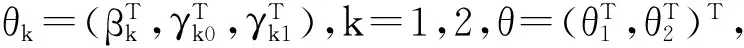
(8)

其中，f(yi|θk)由公式(5)和公式(6)给出。通过式(8)对混合系数π求偏导，得到相应的估计方程为：

但是在实际计算中上式是很难求解的，即使得到混合系数π的相应估值，也可能超出π要求的范围0<π<1。并且传统的极大似然估计是关于式(8)求极大值，但是由于其结构比较复杂，直接求解是相当困难的。所以首先引入指示变量wi，若yi来自第一个混合成分，记wi=1，否则wi=0。这样就可以给出完全数据集Ycom=(Y0,wi)，其中Y0=(yi,Xi,Zi)为观测数据。

基于完全数据的对数似然函数为：

(1-wi)log f(yi|θ2)]}

(9)

可以看出式(9)中的项数比式(8)中的项数有所增加，但是添加的潜在变量是线性的，计算时相对容易。本文将基于公式(9)建立参数极大似然估计的算法。

4 加速MCEM算法

EM算法最初由Dempster等人于1977年首次提出，它是当数据存在缺失时常用的一种迭代算法，由于操作方便且稳定，所以实用性很强。但是传统的EM算法[14-15]只能使得估计收敛到局部极大值，而MCEM算法会大大降低收敛速度。下面提出加速MCEM算法对传统的EM算法和MCEM进行修正[16]。具体就是将MCEM算法与Newton-Raphson算法结合，利用蒙特卡罗法解决高维空间的积分和优化问题，通过某种实验的方法来估算随机变量的期望。该算法具有二次收敛速度，从而使其保留MCEM算法的优点，却改进了MCEM算法的收敛速度。具体算法包括如下3个步骤：

1)E1步。

从条件分布f(wi|θ(t),Y0)中随机地抽取ki个样本。其中θ(t)表示第t次迭代后θ估计的当前值，f(wi|θ(t),Y0)表示在给定当前θ的估计值和观测值Y0下，潜在数据wi的条件预测分布。

2)E2步。

运用步骤1中抽取的ki个样本，令:

(10)

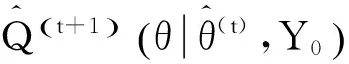
3)M步。

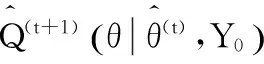
(11)

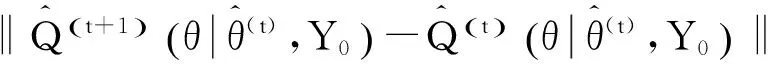
5 模拟研究

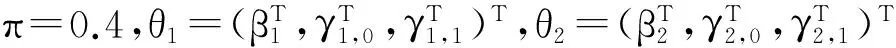
表1 2种算法下的参数估计

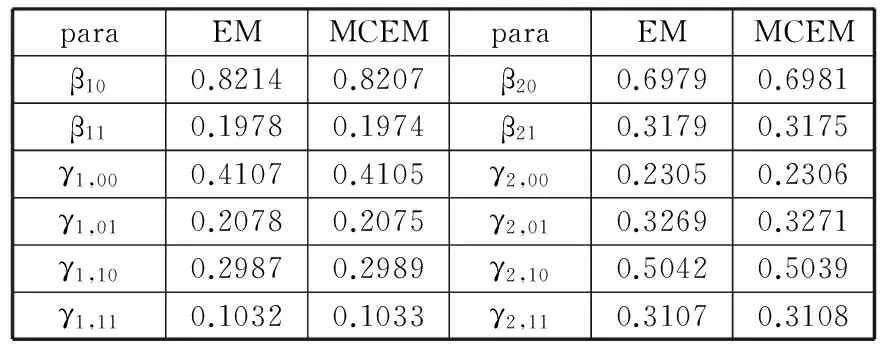
paraEMMCEMparaEMMCEMβ100.82140.8207β200.69790.6981β110.19780.1974β210.31790.3175γ1,000.41070.4105γ2,000.23050.2306γ1,010.20780.2075γ2,010.32690.3271γ1,100.29870.2989γ2,100.50420.5039γ1,110.10320.1033γ2,110.31070.3108

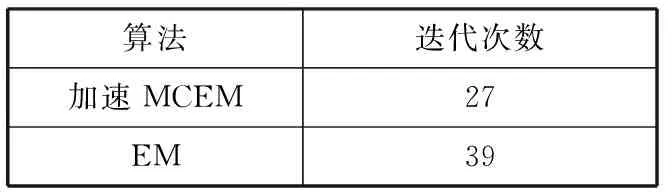
表2 2种算法下的迭代速度

算法迭代次数加速MCEM27EM39

从表1计算结果中容易看出加速MCEM算法在计算的可行性方面表现良好，说明其在E步中使用Monte Carlo模拟所牺牲的精度，在M步中又被补偿了回来。从表2可以看出，在收敛速度方面，加速MCEM算法的收敛速度也优于EM算法。这表明在零一膨胀二项混合回归模型的参数估计问题上，加速MCEM算法无论在计算的可行性方面，还是在收敛速度方面，都有着优于EM算法的表现。

6 结束语

本文首先对存在过多0和1的观测数据提出了零一膨胀回归模型，由于在现实生活中，数据来源于单一总体的假设往往是不成立的，所以进一步引入了零一膨胀二项混合回归模型。针对EM算法通常会使得估计收敛到局部最优解上的缺陷，提出了加速MCEM算法,对具有有限混合成分的ZOIB的参数进行估计。最后通过模拟研究说明该方法的有效性。但是本文并未对混合比例考虑回归，这将是今后的研究重点。

[1] Tchetgen E J, Coull B A. A diagnostic test for the mixing distribution in a generalised linear mixed model[J]. Biometrika, 2006,93(4):1003-1010.

[2] Li Pengfei, Chen Jiahua. Testing the oder of a finite mixture[J]. Journal of American Statistical Association, 2010,105(491):1084-1092.

[3] Zhu Hongtu, Zhang Heping. Hypothesis testing in mixture regression models[J]. Journal of Royal Statistical Society Series B, 2004,66(1):3-16.

[4] Lin T I, Lee J C, Yen S Y. Finite mixture modeling using the skew normal distribution[J]. Statistica Sinica, 2007,17(3):909-927.

[5] Xiang Liming, Yau K K W, Lee A H, et al. Influence diagnostics for two-component Poisson mixture regression models: Applications in public health[J]. Statistics in Medicine, 2005(19):3053-3071.

[6] 陈家骅,李鹏飞,谭鲜明. 混合Von Mises模型的参数估计[J]. 系统科学与数学, 2007,27(1):59-67.

[7] Cohen A. Estimation of the Poisson parameter from truncated samples and from censored samples[J]. Journal of American Statistical Association, 1954,49(265):158-168.

[8] Lambert D. Zero-inflated Poisson regression with an application to defects in manufacturing[J]. Technometrics, 1992,34(1):1-14.

[9] Fahrmeir L, Echavarria L O. Structured additive regression for overdispersed and zero-inflated count data[J]. Applied Stochastic Models in Business and Industry, 2006,22(4):351-369.

[10] Ridout M, Hinde J, Demetrio C G B. A score test for testing zero-inflated Poisson regression model against zero-inflated negative binomial alternatives[J]. Biometrics, 2001,57(1):219-223.

[11] Jansakul N, Hinde J P. Score tests for zero-inflated Poission models[J]. Computational Statistics and Data Analysis， 2002,40(1):75-96．

[12] Melkersson M, Olsson C. Is Visiting the Dentist A Good Habit? Analyzing Count Data with Excess Zeros and Excess Ones[D]. Sweden: Umer University, 1999.

[13] Zhang Chi, Tian Guoliang, Wang Kai. Properties of the zero-and-one inflated Poisson distribution and statistical inference methods[J]. Statistics and Its Interface, 2016,9(1):11-32.

[14] Biernacki C. Initializing EM using the properties of its trajectories in Gaussian mixtures[J]. Statistics and Computing, 2004,14(3):267-279.

[15] 吕敏红,闫奕荣,杨青. 零一膨胀泊松回归模型的EM算法改进[J]. 河南科学, 2017，35(7):1037-1041.

[16] 罗季. Monte Carlo EM加速算法[J]. 应用概率统, 2008,24(3):312-318.

[17] 卢玉桂，韦新星，赵丽棉. 多层线性模参数估计的MCEM算法[J]. 数学的实践与认识, 2016,46(11):225-230.