基于劳伦茨信息值的水下大坝裂缝提取算法

范新南,吴晶晶,史朋飞,张学武

(河海大学物联网工程学院,江苏 常州 213022)

0 引 言

大坝在我国国民经济中发挥着巨大的作用[1]。然而，大坝混凝土面板水位以下部分，由于长期承受很大的水压，经受水的冲刷、渗透和侵蚀，不可避免地会产生裂缝[2]。定时对大坝表面状况进行评估，及时并准确地检测水下大坝表面的裂缝，对保持大坝混凝土的结构健康和延长其使用寿命至关重要。通过光学相机在水下摄取到大坝表面图像，然后对图像进行处理，检测图像中是否存在裂缝，这是目前比较流行的大坝表面缺陷分析方法。相比于传统的视觉检测方法，自动裂缝检测算法过程更加安全、结果更加客观[3-5]。

随着数字图像处理技术的发展，裂缝检测算法在过去的一些年已经得到了巨大的发展[6-8]，并且大多应用于道路裂缝检测、桥体混凝土裂缝检测。但是应用到水下图像的目标检测时，结果却不尽人意。这是由于与自然光照条件下获取的普通图像不同，光在水中传输时，会产生衰减和散射效应，而且水中的悬浮物和水游动植物也会对成像系统造成干扰，这就使得水下图像普遍具有低对比度、模糊不清、光照不均匀、大量随机噪声干扰等特点，大大增加了准确识别裂缝的困难程度。

近年来，业界也有少部分科研人员开始投入到水下大坝裂缝检测，提出了多种算法来提高水下大坝表面裂缝检测的准确性。付军等人[2]提出了基于BP神经网络的大坝裂缝检测算法，该算法通过分析二维图像的亮度值，映射到三维立体表面图像。Cheng等人[9]提出了基于多结构和多规模元素的自适应水下大坝图像裂缝检测算法。马金祥等人[10]则针对水下大坝图像所具有的复杂特征，提出了一种基于暗通道先验的自适应图像增强算法，能有效均衡图像中的光照，并增强裂缝目标区域。张大伟等人[11]则提出了一种基于最大熵原理的改进的Canny算法，使得Canny算子具有自适应性，提高了边缘检测的准确性。但是，当图像背景变化或者是图像中裂缝特征细小、多样化时，大部分的检测算法便不能有效而准确地提取出图像中的裂缝。

针对水下图像的复杂性以及水下大坝裂缝检测所面临的难题，本文提出一种新的基于劳伦茨信息值[12]的水下大坝裂缝提取算法。算法只需要一个先验条件，裂缝是细长形状的。首先从局部出发，采取基于劳伦茨信息值的图像分块裂缝提取方法，将图像分割成大小相等图像块，然后根据每个图像块的劳伦茨信息值，去除确定不含有裂缝信息的图像块，获得可能含有裂缝的图像块。接着，从全局出发，采取基于k均值聚类[13]的裂缝连通域提取方法，根据二值图像中连通域的特征值：圆形度和面积，使用k均值聚类算法得到最终的裂缝区域。

1 劳伦茨信息值

图像f(x,y)的灰度级是m，定义该图像的信息值为PIM，如公式(1)所示。

(1)

其中，h(i)指的是f(x,y)中灰度值为i的像素个数，也就是灰度直方图，其中i∈[0,m-1]。显然，根据公式(1)可知，只有当图像f(x,y)是一个常量级灰度图像时，也就是所有的像素都取同一个灰度值，有PIM(f)=0，此时图像中包含有最小的信息量；只有当h(i)是一个常量时，也就是f(x,y)中的灰度级直方图是均匀分布时，PIM(f)=max ，此时图像包含最大的信息量。因此总结可得，当图像f(x,y)信息量最小时，PIM(f)取得最小值，当f(x,y)信息量最大时，PIM(f)取得最大值[12]。

令图像f(x,y)的像素个数为N(f)，那么定义归一化图像信息值NPIM(f)，如公式(2)所示。

(2)

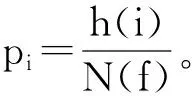
广义的图像信息值PIMk定义为：

(3)

(4)

令Sk=NPIMm-k(f)， 0km，那么有：

(5)

其中，S0S1…Sk…

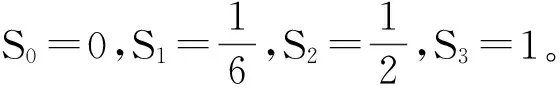
图1 劳伦茨信息曲线

定义劳伦茨信息曲线下的面积为劳伦茨信息值LIM，如图1所示。如果图像的灰度直方图均匀分布，也就是PIM(f)=max ，对应的劳伦茨信息曲线是从(0,0)到(1,1)的直线，也就是图1中的虚线，否则，图像的劳伦茨曲线则会是直线下方的折线。因此，劳伦茨信息曲线可由图像的灰度直方图唯一确定，并且LIM的值越大，代表图像包含更多的信息，LIM的值越小，代表图像包含更少的信息。反之也成立。

本文之所以选择采用LIM，是因为相对于PIM(f)或NPIM(f)来说，LIM是广义的NPIM(f)的定义表现形式，使用更加广泛，并且，LIM可以通过更加直观的劳伦茨曲线图绘制出来，横坐标的取值范围是[0,1]，纵坐标的取值范围也是[0,1]，曲线的性质直接反映出图像信息含量的多少。

2 基于劳伦茨信息值的裂缝提取

图像f(x,y)是已经获取的水下大坝表面的一张比较经典的图像，由于图像是在辅助光的作用下摄取的，背景尤其复杂，具有光照不均匀、对比度低、目标不明显以及大量随机噪声的特点。图像尺寸是629×516，如图2(a)所示。复杂的背景，使得背景和前景的特征差异尤其不明显，大量的干扰，使得准确提取到裂缝更加困难。因此，本文首先采用汪耕任等人[14]的基于粗糙集理论的水下大坝裂缝自适应增强算法对图像作预处理，提高图像的信噪比，均匀背景的光照，降低复杂的背景对裂缝检测造成的负面影响，图像增强效果如图2(b)所示。

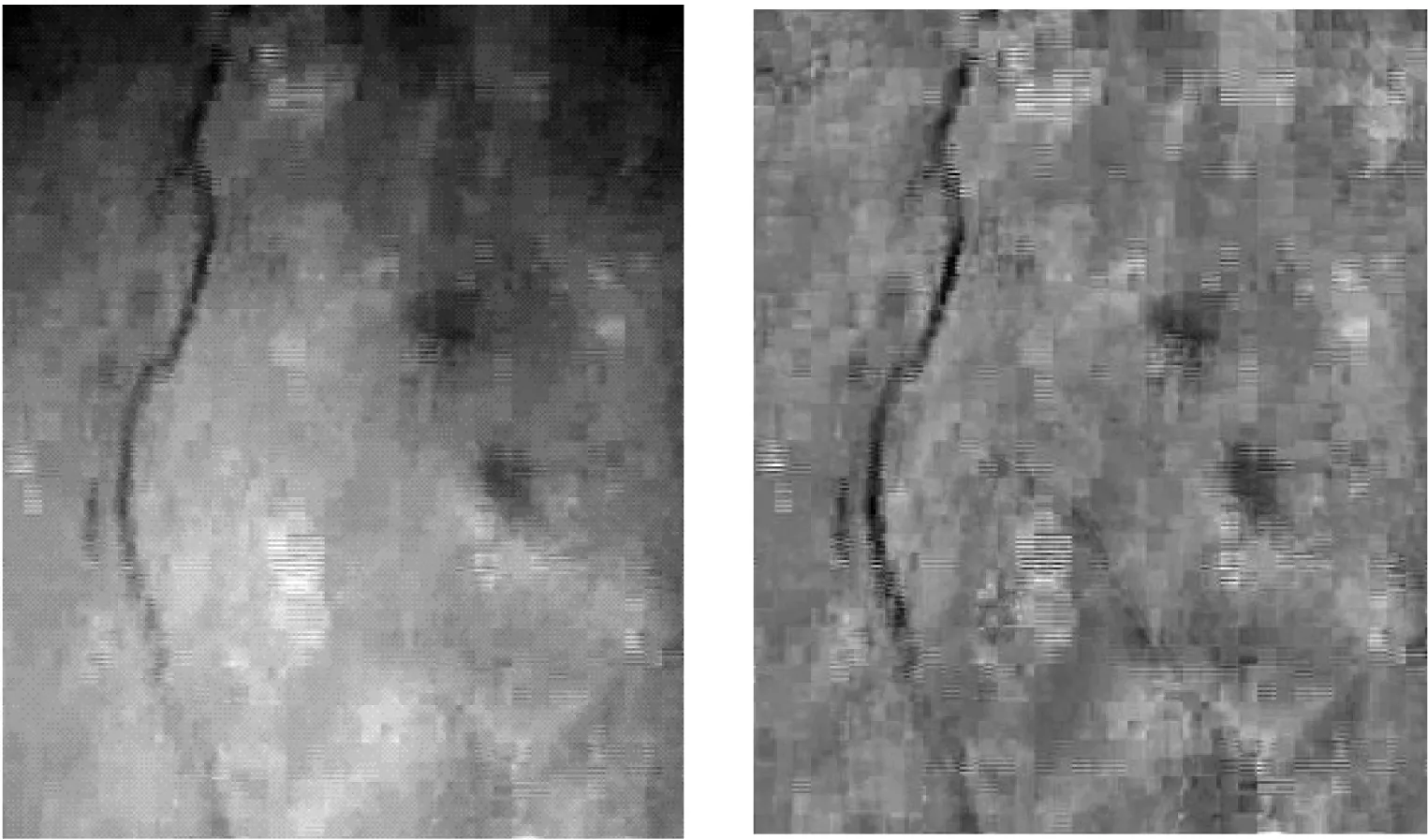
(a) 水下大坝裂缝图像 (b) 预处理后的灰度图像图2 图像预处理

虽然图像经过预处理之后，背景初步得到均衡化，但图像中的目标依然不明显，不同区域内的灰度级相差很大。为了充分利用灰度局部波动信息，将图像分成大小相同的图像块，将每个图像块作为单元分析，可以有效提取出图像块中的目标。由于图像在辅助光的作用下，灰度分布极其不平衡，所以要将图像块的尺寸定义成足够小，才能够充分提取目标信息。这样，便可以大大减小灰度不均衡对目标提取造成的负面影响。但是如果图像尺寸过小，使得图像块中可能只含有裂缝，那么这个图像块的LIM值反而会是最小值，因而会被误判为该图像块中的部分属于纯背景。综合考虑电脑负荷影响裂缝检测的效率以及裂缝的细长特征，本文算法选择15×15的图像块尺寸，若图像尺寸不是15的整数倍，那么图像的最右部分以及最底部分不组成完整的图像块的部分，便剪裁掉，忽略不计。

针对预处理后的图像f(x,y)，图像分块裁剪后，用矩形方框标出所有的15×15图像块，效果如图3(a)所示。

由于图像块的尺寸足够小，所以可以通过LIM值判定对应的图像块中是否含有丰富的图像信息，也就是，该图像块中是否可能存在裂缝。将图像f(x,y)中的每一个图像块看作一个像素，该图像块对应的LIM值看作该像素的灰度值，可以得到一个新的图像f′(x,y)。采用OTSU算法[15]，OTSU算法也称最大类间差法，它按照图像的灰度特性，按值T将图像分为背景和前景2部分，不断遍历使得背景和前景之间的类间方差[15]取得最大值，此时，构成图像的2部分差异最大，相应的T值也就是要求的最佳阈值，根据OTSU算法可以算出f′(x,y)的阈值T。

(a) 图像分块 (b) 分块提取裂缝图3 基于劳伦茨信息值的图像块提取

那么根据劳伦茨信息值的定义，可以得到，LIM>T的图像块含有丰富的图像信息，也就是说可能含有裂缝；LIMT的图像块用矩形方框表示出来，如图3(b)所示。

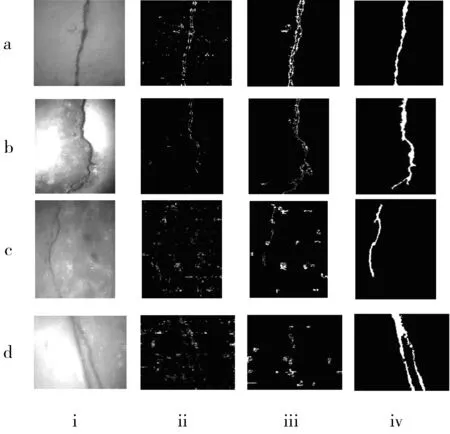
用矩形方框表示出来的图像块是根据图像的LIM值判定可能含有裂缝的图像块，但是由于图像背景复杂，许多含有噪声信息的图像块也被误认为裂缝被提取出来。将f(x,y)中对应的LIM

(a) 二值化图像 (b) 裂缝连通域图4 基于k均值聚类的连通域提取

从局部出发，根据劳伦茨信息值消除一些确认为背景的图像块之后，得到了如图4(a)的可能为裂缝的连通域。但是，这些连通域中有大部分是原图像中的随机噪声以及摄像时的动植物在图像中投下的阴影。为了提高裂缝提取的准确性，算法从全局出发，对连通域的特征作整体的分析。选取面积作第一特征，用A表示；选取圆形度作第二特征，用Round表示，定义如公式(6)所示。

(6)

其中，A指的是连通域的面积，也就是组成该连通域的所有像素的个数；P指的是连通域的周长，也就是连通域边缘所有像素的个数。圆形的值，可以充分体现该连通域与圆形的接近程度。当且仅当Round=1时，该连通域是圆形；Round的值越小，连通域与圆形的差距越大，也就是说是裂缝的可能性越大。

二值图像中连通域的面积和圆形度特征组成二维特征空间，使用k均值聚类算法[13]按二维特征空间将连通域分为2类，一类是裂缝连通域，另一类是干扰连通域。删除被分类为干扰的连通域，得到最终的裂缝区域如图4(b)所示。

3 实验结果与分析

本文的实验图像来源于公伯峡水电站[16]水下缺陷检查项目。该项目的图像是由工作人员用CCD光学相机在水下拍摄获取的。算法的仿真环境是Dell PC：具有2.4 GHz CPU和6 GB RAM的Dell PC，Matlab2013。

为了验证本文提出的算法对于水下大坝图像裂缝检测的有效性和优越性，本文采取与现在流行的算法对比具体图像的提取结果的方法。首先选取4幅具有代表性的裂缝图像。第一幅图像，尺寸是498×529，如图5(ai)所示，背景光照均匀，含有一条普通的裂缝；第二幅图像，尺寸是609×517，如图5(bi)所示，由于辅助光的影响，背景光照非常不均衡，中间部分的亮度要明显暗于两侧边缘部分，图中包含的是剥落型裂缝；第三幅图像，尺寸是629×516，背景呈现绿色色调，图像看似被蒙上一层雾，如图5(ci)所示，图像的对比度非常低，而且图中的裂缝具有细长的特点，使得背景和目标更加难以分离；第四幅图像，尺寸是494×628，图中包含2个裂缝，如图5(di)所示，图中背景光照十分不均匀，而且由于光的散射，图像被雾化，对比度尤其低。这4幅图涵盖了背景各种情况，也具有种类不同、形状不同的各式裂缝，并且图像的尺寸大小不同。

图5 实验结果

对比算法选择目前业内比较流行的2种裂缝检测方式，分别是基于蚁群算法的裂缝检测—ACO[17]和基于边缘检测方法的裂缝检测—WCD[18]。ACO算法是一种以模仿蚂蚁觅食行为手段的优化算法，它对于选取的4幅图像的检测结果如图5(ⅱ)所示；WCD则是通过边缘检测和简单的拟合参数实现了从数字图像中有效地提取目标信息，它对于选取的4幅图像的检测结果如图5(ⅲ)所示；可以看出，这2种算法对于自然光照条件下获取的裂缝图像能取得较满意的效果，但一旦运用到水下获取的大坝表面图像，便会将大量的噪声误检测成裂缝并丢失一部分裂缝信息。本文算法针对水下图像背景复杂、光照不均衡、对比度低等特点，结合预处理、局部和全局检测，得到的最终裂缝区域如图5(ⅳ)所示。

(a) 水下大 坝图像 (b) ACO (c) WCD (d) 本文算法图6 不含有裂缝的大坝表面实验结果图

另外，为了验证算法在图像中不存在裂缝时的表现，本文采用了8幅不含有裂缝的水下坝体图像进行测试，在上述图像上，本文算法均未误检出裂缝。图6显示了在其中一幅图像上的实验结果，图6(a)是原图，图6(b)和图6(c)分别是对比算法ACO[17]和WCD[18]的实验结果，可以发现这2个算法都把噪声误检为裂缝，ACO的虚警率尤其高，图6(d)则是本文算法的实验结果，并未出现误检情况。

实验结果表明，在背景复杂的水下大坝图像中，本文算法能够准确地提取图像中的裂缝并且虚警率低。

4 结束语

本文提出了一种新的基于劳伦茨信息值的水下大坝裂缝提取算法。该算法首先从局部出发，将图像分块，计算图像块的劳伦茨信息值，去除不含有裂缝信息的图像块；接着从全局出发，提取连通域的圆形度、面积组成二维特征空间，采用k均值聚类算法，得到最终的裂缝区域。算法结合了局部分析与全局分析，能够克服水下图像中目标不明显、光照不均衡、噪声严重等问题。实验证明，本文算法能够有效地提取水下大坝图像中的裂缝区域，满足裂缝检测的要求。

[1] 马从计. 水下机器人在大坝水下表面裂缝检测中的应用[J]. 技术与市场, 2012(9):59.

[2] 付军,马从计. 一种新的基于图像处理的水下大坝裂缝检测算法[C]// 中国大坝协会学术年会. 2012.

[3] Cheng H D, Chen J R, Glazier C, et al. Novel approach to pavement cracking detection based on fuzzy set theory[J]. Journal of Computing in Civil Engineering, 1999,13(4):270-280.

[4] Prasanna P, Dana K J, Gucunski N, et al. Automated crack detection on concrete bridges[J]. IEEE Transactions on Automation Science & Engineering, 2016,13(2):591-599.

[5] Fujita Y, Mitani Y, Hamamoto Y. A method for crack detection on a concrete structure[C]// Proceedings of the 18th International Conference on Pattern Recognition. 2006:901-904.

[6] Subirats P, Dumoulin J, Legeay V, et al. Automation of pavement surface crack detection using the continuous wavelet transform[C]// 2006 IEEE International Conference on Image Processing. 2007:3037-3040.

[7] Miguel G, David B, Oscar M, et al. Adaptive road crack detection system by pavement classification[J]. Sensors, 2011,11(10):9628-9657.

[8] Shi Yong, Cui Limeng, Qi Zhiquan, et al. Automatic road crack detection using random structured forests[J]. IEEE Transactions on Intelligent Transportation Systems, 2016,17(12):3434-3445.

[9] Chen Congping, Wang Jian, Zou Lei, et al. Underwater dam image crack segmentation based on mathematical morpholog[J]. Applied Mechanics & Materials, 2012,220-223:1315-1319.

[10] 马金祥,范新南,吴志祥,等. 暗通道先验的大坝水下裂缝图像增强算法[J]. 中国图象图形学报, 2016,21(12):1574-1584.

[11] 张大伟,许梦钊,马莉,等. 水下大坝裂缝图像分割方法研究[J]. 软件导刊, 2016,15(9):170-172.

[12] Abutableb A S. Automatic thresholding of gray-level pictures using two-dimensional entropy[J]. Computer Vision Graphics & Image Processing, 1989,47(1):22-32.

[13] Boutsidis C, Magdon-Ismail M. Deterministic feature selection for K-means clustering[J]. IEEE Transactions on Information Theory, 2013,59(9):6099-6110.

[14] 汪耕任,范新南,史朋飞,等. 基于粗糙集理论的水下大坝裂缝图像增强算法[J]. 计算机与现代化, 2015(9):35-41.

[15] Otsu N. A thresholding selection method from gray-level histogram[J]. IEEE Transactions on Systems Man & Cybernetics， 1979,9(1):62-66.

[16] 何建辉,王龙. 公伯峡水电站计算机监控系统[J]. 西北水电, 2005(1):70-72.

[17] Dewan S, Bajaj S, Prakash S. Using ant’s colony algorithm for improved segmentation for number plate recognition[C]// 2015 IEEE/ACIS 14th International Conference on Computer and Information Science (ICIS). 2015:313-318.

[18] Hu Dongna, Tian Tian, Yang Hengxiang, et al. Wall crack detection based on image processing[C]// 2012 3th International Conference on Intelligent Control and Information Processing(ICICIP). 2012:597-600.