基于动作的动态空间推理
2018-03-29谢玉枚高海燕
谢玉枚,高海燕
(1.福建江夏学院电子信息科学学院,福建 福州350108; 2.厦门学院电气与自动化学院,福建 厦门 361024)
0 引 言
虽然现阶段在定性空间推理中有一套相对成熟的表示模型和推理方法,但是空间信息的表达和推理强调的往往是静态空间的配置。在实际应用中,多数智能系统处理的定性空间信息都是动态变化的,动态空间信息的表达和推理尤为重要。特别是近年来,动态定性空间推理的研究在定性空间领域得到越来越多的关注,已经成为定性空间推理中的研究热点[1]。
大多数应用领域涉及空间、动作和空间变化的交互[2],例如机器人导航、协同自治Agent和自动规划等领域,它们需要处理的动态变化空间信息通常是由动作造成的。时间信息隐藏在动态变化的状态中,并非单独出现。而动态关系变化的研究主要侧重于动作产生的空间关系的改变,因此不需要在已经很复杂的空间表示中再加入时间维度,时空信息的表示推理变得简单很多。
Freksa[3]所提出的概念邻域图在研究动态空间关系变化的方法中得到广泛应用,几乎所有的定性空间推理模型中有概念邻域图的表示。一系列处理变化的动态空间关系的方法在此基础上提出[4-6]。2006年,Bhatt等人[7]用场景演算对空间拓扑关系的变化进行形式化描述,同时表示了空间推理中的基本概念空间关系约束、复合表和概念邻域图,但是没有对引起空间拓扑关系变化的动作和事件具体表示和分析。2007年,Delafontaine等人[8]提出了在动态变化的拓扑关系网络中移动实体的定性关系变化的研究方法,用定性轨道关系表示在网络中移动点之间的关系。他定义了网络中发生动态变化时2个移动点之间的关系变化,这种变化必须是连续的。2008年,Bhatt等人[1]用场景演算对动态空间系统进行建模,提出动态空间系统建模的通用框架,定义多类逻辑语言对动作和事件进行形式化表示,它能表示空间的各个方面,如空间关系的不同方面、物理属性、空间属性等,但他同样没有对动作、事件、空间关系和应用场景具体化。2010年,Bhatt[9-10]提出一种集成推理方法可作为一个有用范例使得定性空间表达和推理技术可广泛用于动态GIS智能环境、认知机器人和空间设计的应用,并且这种范例支持解决动态空间系统建模的形式化并保证了空间推理领域、动作和变化推理领域和常识性推理之间的交互。在应用方面,Suhan等人[11]在动态空间系统的基础上提出了一种基于归纳逻辑规划的归纳时空学习框架。Waga等人[12]在动态空间系统的系统建模的需求上,提出非单调空间推理原型。
国内定性空间推理的研究方向集中于多方面空间关系结合的表示和推理、方向关系建模和异构定性空间推理等领域。目前研究动态空间推理的人比较少,梁晶晶[13]用区间概念邻域图表示空间变化过程,用空间关系在概念邻域的变化次数表示时间,求若干时间后空间关系的变化,因为时间是用简单定量表示,这种动态推理简单。Song等人[14]用概念邻域划分表来刻画空间关系与动作之间的转换关系,给出了状态动作表,用完备互斥的空间关系集合以及其领域划分图来描述定性空间关系的规划问题,提出了规划求解方法,但是其针对的是单个空间关系,相对简单。杨帅[15]通过对动态空间中区间的空间结构进行划分,提出了基于交集矩阵的运动区间与静止区间统一表达模型UMMS,成功区分和识别出共计49种基本区间关系。为了进一步研究区间关系的动态变化,分析了这些关系的概念邻域关系并给出有向概念邻域图。在应用方面Zhou等人[16]基于地理视频本体论的基础上,利用时空推理模型实现视频数据的聚集。
综上所述,动态空间推理是定性空间推理的研究热点,目前还处于起步研究阶段,大多数研究仅限于提出动态空间推理的框架和相关可能的应用场景,没有对其中的动作、事件、空间关系具体化和动作作用下多个空间实体间空间关系改变情况[17]。
本文以动态空间信息的表示和推理为研究背景,研究在二维平面中拥有多个区域实体的空间场景下基于动作的动态空间推理问题。本文具体的安排如下:1)介绍动态空间推理的研究现状;2)定义空间场景中的动作和给出区间关系的状态转移图;3)对Bhatt定义的动态空间系统进行细化和扩展,用一个元组对动态空间系统中的空间场景进行形式化表示;4)介绍实体在历史场景中发生移动动作推出新空间场景的方法,同时给出一个应用场景;5)对本文的主要内容进行总结,并对下一步的工作进行展望。
1 动作及区间关系的状态转移图
空间实体在现实生活的移动极为常见,比如从图书馆到宿舍、天空中的云朵在不停地漂移和机器人导航中机器人的移动都是移动动作。移动的结果就是空间实体自身位置的改变,从而与空间场景中其他实体的空间关系也发生了变化,进入新的空间场景。
假设空间实体在移动地过程中大小不发生变化,在二维平面中,对移动动作进行分析和总结,可以得到8个移动动作如定义1~定义8所示。空间实体在二维平面中发生移动,其空间位置发生变化,所以以下8个移动动作表现为空间实体在X轴和Y轴上发生位置改变。
定义1动作谓词MW,MW(A)表示实体A大小不变,A在Y轴上的坐标不变,X轴上的坐标向西移动。
定义2动作谓词MN,MN(A)表示实体A大小不变,A在X轴上的坐标不变,Y轴上的坐标向北移动。
定义3动作谓词ME,ME(A)表示实体A大小不变,A在Y轴上的坐标不变,X轴上的坐标向东移动。
定义4动作谓词MS,MS(A)表示实体A大小不变,A在X轴上的坐标不变,Y轴上的坐标向南移动。
定义5动作谓词MNW,MNW(A)表示实体A大小不变,A在X轴上的坐标向西移动,Y轴上的坐标向北移动。
定义6动作谓词MNE,MNE(A)表示实体A大小不变,A在X轴上的坐标向东移动,Y轴上的坐标向北移动。
定义7动作谓词MSE,MSE(A)表示实体A大小不变,A在X轴上的坐标向东移动,Y轴上的坐标向南移动。
定义8动作谓词MSW,MSW(A)表示实体A大小不变,A在X轴上的坐标向西移动,Y轴上的坐标向南移动。
从上述定义可以看出对于MNW,MNE,MSE和MSW可认为在实体A上同时发生了2个移动动作。例如MNW(A)可以看成是实体A上发生了移动动作MN和MW,因此在下面分析空间实体在移动动作作用下的状态转移图也只考虑MN,ME,MS和MW动作谓词;MNW,MNE,MSE和MSW看成是MN,ME,MS和MW之间两两相互组合。
本文研究动态空间系统中基于动作的动态空间推理问题,即在一个空间场景中有多个实体,空间场景发生变化的原因是由于空间实体发生了动作,在上面的论述中把广度意义上的动作抽象为8个移动动作,空间实体发生动作后,空间实体间的空间关系会发生怎样的改变呢?
在以区域为空间原语中,某一个空间实体发生移动动作,这个实体与空间场景中其他实体的空间关系可能发生改变,从而得到新的空间场景。在这里没有对实体发生动作的时间进行量化,而是对其进行定性化处理,认为发生动作的实体与空间场景中剩余实体的空间关系只要一个或多个发生变化,就认为是进入下一时刻,得到新的空间场景。
对于空间原语实体为区域的空间实体,用MBR近似空间区域,用矩形关系表示空间实体空间关系,在表达上简单明了,易于理解。因为在二维空间的每个坐标轴上使用区间代数的理论,从而形成矩形代数理论,其中的关系就是矩形关系,空间实体在动作作用下的矩形关系变化表现为X轴和Y轴方向上区间关系的变化,所以本文只研究区间关系在动作作用下的变化的情况。
区间代数因有13个区间关系,在区间代数中m,mi,s,si,f,fi,eq是不稳定关系,所谓不稳定关系就是一旦相关的空间实体发生了移动动作,下一时刻空间关系肯定改变;而p,pi,d,di,o,oi是稳定关系,当相关空间实体发生移动动作,下一时刻空间关系有可能还是原来的空间关系。如图1~图2所示为区间关系在动作作用下的状态转移图,其中ME和MN动作的状态转移图相同,MW和MS动作的状态转移图相同。它由节点和有向边组成,节点表示空间关系,节点之间有有向边相连表示在动作作用下下一时刻的空间关系,而如果节点之间要经过多条有向边才能到达,则表示实体间的空间关系需要经过多次的动作才可以到达。
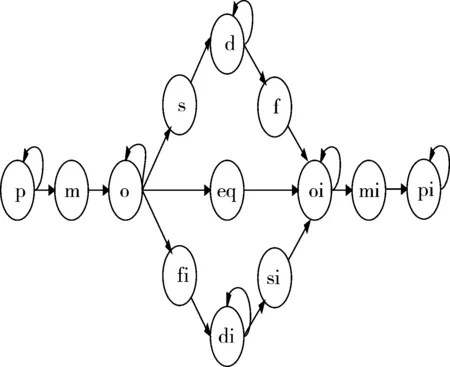
图1 ME/MN区间关系状态转移图
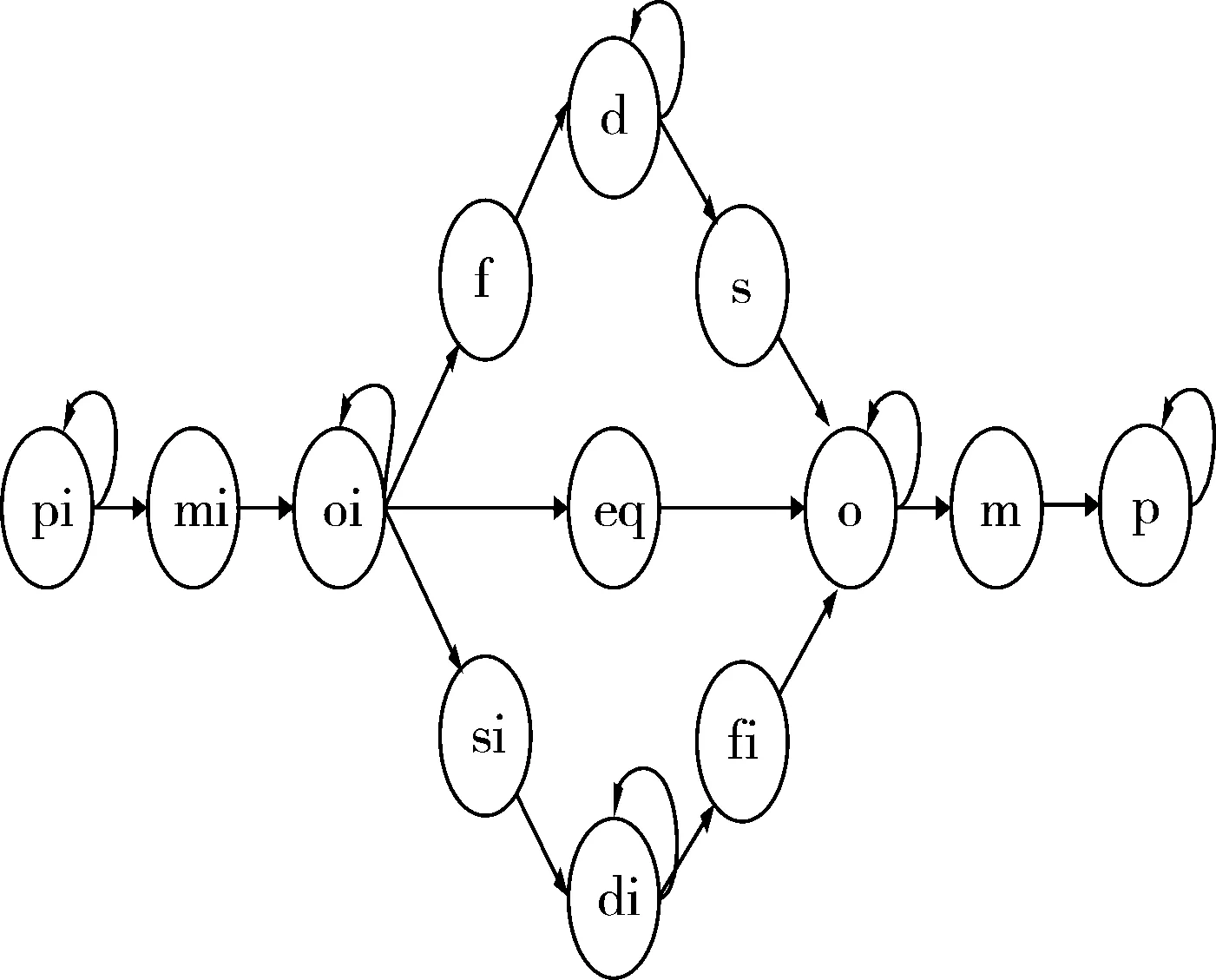
图2 MW/MS区间关系状态转移图
区间关系的状态转移图和区间关系概念邻域如图3所示,看上去很类似,除去有些区间关系自身到自身,把图1和图2合并起来就是区间关系概念邻域图。区间关系概念邻域图也没有对时间定量化,研究2个空间实体间空间关系的连续变化。同时也是由边和节点组成,不同的是区间关系状态转移图是有向边,因为本文研究空间关系在动作作用下的迁移,而区间关系概念邻域图没有涉及动作,只是基于空间关系的连续变化。区间关系的状态转移图和区间关系概念邻域图还有一个重要的不同是:区间关系的状态转移图对应的是拥有多个空间实体的空间场景下一个空间实体动作后,下一个时刻空间场景中空间关系的变化;而区间关系概念邻域图只研究2个空间实体的空间关系变化,不涉及其他空间实体。

图3 区间关系的概念邻域图
定义9动作作用下状态转移函数。Nbr(R,M)={在M动作下的状态转移图上的空间关系r指向的所有基本关系|r∈R}。
给定M动作下的状态转移图和指定要求解的空间关系集合R,通过对R中每个原子关系调用状态转移函数,所得的每个结果之间进行析取即为整个集合的动作M作用后的状态转移关系,如表1所示为区间关系每个原子关系的状态转移关系。例如求R={p,eq},M=ME时其状态转移关系,通过查表1可得其状态转移关系是:{p,m}∪{oi}。“动作作用下状态转移函数”在空间实体发生动作后新的空间场景的求解中经常用到。
表1 区间关系状态转移表

区间关系动作ME/MNMW/MSp{p,m}{p}pi{pi}{pi,mi}m{o}{p}mi{pi}{oi}o{o,s,eq,fi}{o,m}oi{oi,mi}{oi,si,eq,f}s{d}{o}si{oi}{di}d{d,f}{d,s}di{di,si}{di,fi}f{oi}{d}fi{di}{o}eq{oi}{o}
举例说明其在动态空间推理中的应用。例如实体A和B的矩形关系为(o,m),实体A向东移动后,求下一时刻的A和B的空间关系。因为是向东移动,所以Y轴空间关系不变,对于X轴点区间关系如表1所示,区间关系o在ME作用下有4种情况分别是:{o,s,eq,fi},所以实体A向东移动后的空间关系是:(o,m)∪(s,m)∪(eq,m)∪(fi,m)。
例如实体A和B的矩形关系为(o,m),实体A向西南移动后,求下一时刻的A和B的空间关系。因为是向西南移动,可以分解成MW和MS这2个动作组合,所以对于X轴点区间关系如表1所示,区间关系o在MW作用下有2种情况为:{o,m};对于Y轴点区间关系如表1所示,区间关系m在MS作用下只有一种情况为:{p},所以实体A向西南移动后的空间关系是:(o,p)∪(m,p)。
2 空间场景进行形式化表示
客观世界是不断变化的,空间场景也同样不断地发生着各种各样的变化。在定性空间推理中,大多数研究的焦点是静态空间推理问题,即用定性空间关系表示空间实体间的关系,并在此基础上研究复合运算、复合表和一致性判断等问题。然而,当前面临的问题是在一个动态变化的空间环境中,人们应该如何对动态变化的空间环境进行定义?如何对引起空间关系变化的原因进行表示?
Bhatt等人[1]定义的动态空间系统为在事物的内部作用和外部作用下空间配置发生变化和迁移的空间系统,其中空间配置由空间关系集合表示。该定义中空间关系集合是动态空间的基础,用空间关系描述动态空间系统的属性,并确定空间关系的改变是由于自身或外力的作用。
一般意义上的空间在事物活动中处于基本地位,物体在空间位置上发生各种动作。动态空间系统中所说的空间不仅仅是一般意义上的空间,空间实体还可以是具有行为和感知能力的实体,例如空间实体可以是人、移动的车辆和机器人等。
在一个动态空间系统中,各种空间关系随时间发生变化,其中有的是自然界中无序的自发的,但更多的是有序的,带有目的性的,例如大楼中人群的疏散和在空间环境中机器人地图的学习。空间关系发生的改变必然是与动作或者事件相联系的,可以是空间实体自身发生动作,也可以是空间实体在外力作用下发生动作。总之最后的结果是发生动作的空间实体与空间场景剩余空间实体的空间关系发生了改变。
空间关系是动态空间系统的基础,空间有不同方面包括拓扑和方向等,用哪种空间关系更符合人们常识,同时易于计算和空间各方面转换呢?这与特定动态空间系统完成的功能相关。
通过以上对动态空间系统的论述,对Bhatt定义的动态空间系统进行细化和扩展。动态空间系统是由空间场景构成,动作可以引起空间场景的改变。空间场景包含空间实体、空间关系和空间实体上所允许的动作。空间实体在动作作用下使空间场景发生改变,从而达到一定目标。其中空间实体是包含带有行为和感知能力的空间实体以及一般的空间实体。这里论述的动态空间系统是个不针对特定领域、完成特定任务的空间系统,它是一个通用的空间系统。
在动态空间系统中,空间场景表示其基本属性,空间场景包括了空间实体、实体间定性空间关系和空间实体所允许的动作,用一个元组表示空间场景。定义如下:
定义10空间场景用一个元组S表示,S=
在基于动作的动态定性空间推理中,B是由所选择的空间模型给出的,本文用矩形关系表示实体的空间关系,所以B为矩形关系。A是第1章所定义的8个动作。T是B对应的状态转移表。
在动态空间系统中,空间场景描述了空间实体的空间关系及实体可允许的动作,它有一个基本问题需要解决:实体在历史场景中发生移动动作推出新空间场景。倘若允许多个空间实体同时发生动作,同时发生动作的实体需要研究它们相对动作下的空间关系变化,若没有特定领域约束,问题变得特别复杂,所以这里假定只有一个实体发生动作。
定义11Do(S,m,M)是在空间场景S中,空间实体m发生动作M,下一个时刻新的空间场景。
例如如图4所示的空间实体分布,实体o1发生向东南方向移动动作后得到新的空间场景可表示为Do(S,o1,MSE)。若空间实体连续发生动作,则可以得到动态空间系统中的空间场景序列{S1,S2,S3,…,Sn}。

图4 区域空间实体分布图
3 动作推出新空间场景
由定义11可知Do(S,m,M)是空间场景S在空间实体m发生动作M后下一个时刻的空间场景,空间场景S到新空间场景空间变化的改变只能是与实体m相关空间关系的改变。若已知空间场景中有n个空间实体,因为空间场景给定的是完全约束集,与实体m相关的n-1个空间关系可能发生变化(当然它自身与自身的关系在动作下不发生改变),所以只研究这n-1个空间关系在动作作用下的情况就可以得到新空间场景。
用矩形关系表示空间场景中实体的空间关系,因此可以把动作划分为X轴方向动作Mx和Y轴方向动作My,研究实体m与场景中实体的X轴定性关系Rmx[ ]和Y轴定性关系Rmy[ ]在Mx和My作用下的NX[ ]和NY[ ]。若给定n个空间实体,则Rmx[ ]和Rmy[ ]的个数都为n,所求的NX[ ]和NY[ ]的个数也为n。根据给定S,m,M有以下步骤:
1)提取Mx,My,Rmx[ ]和Rmy[ ];
2)若Mx!=null,根据Mx下的状态转移表得到满足路径一致性要求的、实体m与空间场景中剩余实体的X轴定性关系NX[ ];
3)若My!=null,根据My下的状态转移表得到满足路径一致性要求的、实体m与空间场景中剩余实体的Y轴定性关系NY[ ];
4)若Mx!=null && My!=null,则NX[ ]与NY[ ]组合,更新空间场景;
5)若Mx!=null && My==null,则NX[ ]与Rmy[ ]组合,更新空间场景;
6)若Mx==null && My!=null,则Rmx[ ]与NY[ ]组合,更新空间场景。
需要注意的是,因为Do(S,m,M)是求下一时刻的新空间场景,根据下一个时刻的概念,当场景中有一个空间关系发生改变时,就认为是进入新空间场景。若Mx不等于null时Rmx[ ]有一个或多个不稳定关系,此空间关系根据在Mx下的状态转移表得到定性关系,剩余不稳定关系保持不变,因为不稳定关系在动作作用下只有一个定性关系,所以可得到唯一的NX[ ];若Rmx[ ]所有关系都是稳定关系,那么每一个稳定关系通过在Mx下的状态转移表得到一个空间关系集,从每一个空间关系集中选择一个定性关系使得满足路径一致的要求可到NX[ ],符合要求的关系序列NX[ ]可能不止一个。
方法1动作推理方法ActionReason(S,m,M)
输入:空间场景S,发生动作实体m和发生的动作M。
输出:实体m发生动作M后新的空间场景。
说明:valid(N[ ][ ])是判断所选择关系是否对空间场景是路径一致的。
Nbr(r,M)是关系r在动作M后空间关系集合,由表1状态转移表获得:
1)对输入动作M进行X轴和Y轴划分得到Mx和My;
2)根据场景S和动作实体m得到Rmx[ ]和Rmy[ ];
3)若Mx!=null,判断Rmx[ ]中是否有不稳定关系;
①若有,当Rmx[i]为不稳定关系,则NX[i]= Nbr(Rmx[i],Mx);当Rmx[j]为稳定关系,令NX[j]=Rmx[j]。得到唯一NX[ ],转到步骤5;
②否则转到步骤4;
4)对于每一个Rmx[i],可以得到空间关系集合Nx[i][ ]=Nbr(Rmx[i],Mx),从而可得到NX[ ]=valid(Nx[ ][ ]);
5)若My!=null,判断Rmy[ ]中是否有不稳定关系;
①若有,当Rmy[i]为不稳定关系,则NY[i]= Nbr(Rmy[i],My);当Rmy[j]为稳定关系,令NY[j]=Rmy[j];得到唯一NY[ ],转到步骤7;
②否则转到步骤6;
6)对于每一个Rmy[i],可得到空间关系集合Ny[i][ ]= Nbr(Rmy[i],My),从而可得到NY[ ]=valid(Ny[ ][ ]);
7)若Mx!=null && My!=null,则NX[ ]与NY[ ]组合,更新空间场景;
8)若Mx!=null && My==null,则NX[ ]与Rmy[ ]组合,更新空间场景;
9)若Mx==null && My!=null,则Rmx[ ]与NY[ ]组合,更新空间场景;
10)返回。
对于valid (N[ ][ ])有:
输入:Rmx[ ](Rmy[ ])的空间关系集。
输出:满足路径一致性要求的关系集。
1)对于每一个定性关系集合N[0][ ],…,N[n-1][ ]选择一个区间关系,得到n个定性系列M[ ];
2)对于一个M[i], 0≤i ①对于一个M[j], i a 判断M[i]-1。M[j]∧Rx[i,j]==1是否为真; b 若为真,j++; c 若为假,退出循环转到步骤1,重新选择一组M[ ]。 ②i++; 3)得到满足一致性要求的M[ ]。 对于输入空间原语为区域的空间实体,若有如图4所示的空间实体分布,图4中空间实体的完全约束关系集如表2所示。 表2 空间关系完全约束集 o1o2o3o4o1(eq,eq)(fi,fi)(di,si)(di,di)o2(f,f)(eq,eq)(pi,pi)(pi,pi)o3(d,s)(p,p)(eq,eq)(p,p)o4(d,d)(p,p)(pi,pi)(eq,eq) 在图4所示实体分布下求Do(S,o4,MNE)可知m=o4,M=MNE,得到R4x[0]=d,R4x[1]=p,R4x[2]=pi,R4x[3]=eq,都是稳定关系;R4y[0]=d,R4y[1]=p,R4y[2]=pi,R4y[3]=eq,都是稳定关系。 因为M=MNE,可以看成是ME和MN共同作用,所以R4x[ ]在ME作用下Nx[0][ ]={d,f},Nx[1][ ]={p,m},Nx[2][ ]={pi},Nx[3][ ]={eq};R4y[ ]在MN作用下Ny[0][ ]={d,f},Ny[1][ ]={p,m},Ny[2][ ]={pi},Ny[3][ ]={eq}。 通过一致性检测满足要求的有:NX[ ]={d,p,pi,eq}∨{d,m,pi,eq};NY[ ]={d,m,pi,eq}∨{d,p,pi,eq}。NX[ ]和NY[ ]通过组合可以得到4种空间场景,其中一种与原来空间场景一样,所以新的空间场景S1有3个,如表3~表5所示,其动作后实体分布如图5所示,符合实体o4发生动作MNE后的实体分布。 方法1 ActionReason(S,m,M)用于求空间场景S中一个空间实体m发生动作M后的新空间场景,若有多个空间实体同时发生动作,要考虑同时动作实体在相对动作作用下的空间关系变化,若没有给定领域约束条件将很难求解。本文的研究不是针对特定的应用场景,没有领域约束,所以方法1只能适用于一个实体发生动作。 表3 o4发生动作MNE后S1完全空间关系约束集(1) o1o2o3o4o1(eq,eq)(fi,fi)(di,si)(di,di)o2(f,f)(eq,eq)(pi,pi)(pi,mi)o3(d,s)(p,p)(eq,eq)(p,p)o4(d,d)(p,m)(pi,pi)(eq,eq) 表4 o4发生动作MNE后S1完全空间关系约束集(2) o1o2o3o4o1(eq,eq)(fi,fi)(di,si)(di,di)o2(f,f)(eq,eq)(pi,pi)(mi,pi)o3(d,s)(p,p)(eq,eq)(p,p)o4(d,d)(m,p)(pi,pi)(eq,eq) 表5 o4发生动作MNE后S1完全空间关系约束集(3) o1o2o3o4o1(eq,eq)(fi,fi)(di,si)(di,di)o2(f,f)(eq,eq)(pi,pi)(mi,mi)o3(d,s)(p,p)(eq,eq)(p,p)o4(d,d)(m,m)(pi,pi)(eq,eq) 图5 实体o4发生动作MNE后新空间场景 在一个动态空间环境中,有n个空间实体,初始空间场景中a和b空间关系为R(a,b)=R1。当a发生移动动作序列,求从R(a,b)=R1到R(a,b)=R2的过程中的一个空间场景序列。这在机器人导航中有重要的应用,这个问题可以转化为Agent从位置L1到位置L2移动过程中的空间关系变化过程。 例如,如图4所示空间实体分布,若o2要到达o3的西南方,求o2移动过程中空间场景序列。图4中R1=(pi,pi),因为o2要到达o3的西南方,通过查矩形关系与方向关系对应表可得到R2=(p,p)。从R1到R2变化过程中,X轴方向上是pi到p,由区间关系的状态转移图可知o2在X轴方向发生的动作是Mx=MW;Y轴方向上是pi到p,由区间关系的状态转移图可知o2在Y轴方向发生的动作是My=MS。o2要到达o3的西南方,o2可选择多种动作序列例如{MSW,MSW,…},{MW,MW,…,MS,MS,…},{MS,MS,…,MW,MW,…}等。由o2选择的移动动作序列,可以得到一序列空间场景序列,这些空间场景序列描述着o2从一个位置L1到位置L2空间场景的改变过程。 本文在定性空间推理基础上,研究拥有多个空间实体的空间场景下基于动作的动态空间推理问题。定义了空间实体的8个移动动作,给出了空间实体在动作作用下的状态转态图和状态转移表,并对概念邻域图和状态转移图进行对比,指出其相同点和不同点。用一个元组对动态空间系统中的空间场景进行形式化表示,提出了由实体移动动作推出新空间场景方法,并指出方法的局限和不足,同时给出一个应用场景。以概念邻域图为基础研究单个空间关系变化问题相比复杂度有所提高,对动态空间推理和表示有一定的理论和实际应用价值。 动态定性空间推理已经成为定性空间推理中的研究热点,且其关乎到实际应用。本文对动态空间系统的论述不太全面,随着动态空间推理技术的发展,对动态空间系统应该有更深的认识和研究。在实际应用中存在多个实体同时发生动作,且其作用在实体的时间都不一样,所以情况就非常复杂,对所提方法缺乏数学的证明,这些都是下一步要做的工作。 [1] Bhatt M, Loke S. Modelling dynamaic spatial systems in the situation calculus[J]. Spatial Cognition and Computation, 2008,8(1-2):86-130. [2] Bhatt M, Guesgen H, Wolfl S, et al. Qualitative spatial and temporal reasoning: Emerging applications,trends,and directions[J]. Spatial Cognition & Computation, 2011,11(1):1-14. [3] Freksa C. Conceptual neighborhood and its role in temporal and spatial reasoning[M]// Decision Support Systems and Qualitative Reasoning. 1991:181-187. [4] Egenhofer M J, Al-Taha K K. Reasoning about gradual changes of topological relationships[M]// Theories and Methods of Spatio-temporal Reasoning in Geographic Space. 1992:196-219. [5] Rajagoplan R. A model for integrated qualitative spatial and dynamic reasoning about physical systems[C]// Proceedings of the 12th National Conference on Artificial Intelligence(AAAI-94). 1994:1411-1417. [6] Dylla F, Moratz R. Exploiting qualitative spatial neighborhoods in the situation calculus[C]// Proceedings of the 4th International Conference on Spatial Cognition IV Reasoning, Action, Interaction. 2004:304-332. [7] Bhatt M, Rahayu W, Sterling G. Qualitative spatial reasoning with topological relations in the situation calculus[C]// Proceedings of the 19th International Florida Artificial Intelligence Research Society Conference. 2006:713-718. [8] Delafontaine M, Weghe N V D, Bogaert P, et al. Qualitative relations between moving objects in a network changing its topological relations[J]. Information Sciences, 2008,178(8):1997-2006. [9] Bhatt M. Reasoning about Space, actions, and change: A paradigm for applications of spatial reasoning[M]// Qualitative Spatio-temporal Representation and Reasoning: Trends and Future Directions. 2012:284-320. [10] Bhatt M. Commonsense inference in dynamic spatial systems: Epistemological requirements[C]// The 23rd International Florida Artificial Intelligence Research Society Conference (FLAIRS 2010). 2010:3-20. [11] Suchan J, Bhatt M, Schultz C. Deeply semantic inductive spatio-temporal learning[C]// The 26th International Conference on Inductive Logic Programming. 2016:73-80. [13] 梁晶晶. 空间推理中多种空间关系结合和时空变化的研究[D]. 西安:西安交通大学, 2011. [14] Song Xiaohua, Quyang Dantong. Automated planning method for dealing with dynamic spatial relations[J]. Journal of Software, 2012,23(10):2564-2571. [15] 杨帅. 动态空间中运动区间与静止区间统一表达模型的研究[D]. 长春:吉林大学, 2014. [16] Zhou Yan, Wang Zhe, He Di. Spatial-temporal reasoning of Geovideo data based on ontology[C]// 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). 2016:4470-4473. [17] Bhatt M, Guesgen H, Hazarika S. Proceedings of the workshop on Spatio-Temporal dynamics(STeDy)[C]// IJCAI 2015: International Joint Conference on Artificial Intelligence(Buenos Aires, Argentina). 2015.




4 结束语
