基于模糊神经网络PID的舵机控制系统
2018-03-29卜庆伟柴金宝崔二伟
卜庆伟,陈 雄,柴金宝,崔二伟
(南京理工大学航空宇航系,江苏 南京 210094)
0 引 言
近年来,随着现代战争对武器科技水平的要求越来越高,高精度制导技术已经成为国家制导导弹研究的重要方向。舵机是导弹制导系统的执行部件,舵机系统控制技术的水平不仅影响导弹的空中飞行姿态,而且在极大程度上决定了导弹的制导精度,因此,提高舵机系统的整体性能具有非常重要的意义。
直流无刷伺服舵机作为当前应用最广泛的制导导弹控制元件,具有低质量、体积小、高转速和能实现较大的转矩输出等特点[1]。传统的直流无刷舵机一般采用PID控制方式,该控制算法具有结构简单、参数调整方便、易于实现等优点,但其本质是一种线性控制,而直流无刷舵机是一个多变量、非线性、时变的复杂系统,传统PID控制算法对该复杂系统的特性变化不敏感,在实际中,往往达不到预期的控制效果[2-3]。模糊PID控制器可以改善传统PID控制效果,但其获取知识比较繁琐,模糊规则和模糊隶属度函数的调节主要依靠相关操作人员的经验[4],具有较大的主观性,自学习能力较差。神经网络具有很高的自适应学习能力和非线性映射能力,然而其不适于表达基于规则的知识,系统行为不可理解,难以充分检验。
鉴于上述神经网络控制和模糊PID控制方式的优缺点,本文设计一种改进的模糊神经网络PID控制器,将模糊PID控制和神经网络控制适当地结合起来,吸取两者的长处,使其同时具备模糊系统的逻辑推理能力,能够有效地利用已有知识经验,又具备神经网络的自适应学习能力[5],能够及时调整自身的控制规则和参数,最终满足控制系统对快速性和准确性的要求。
1 舵机控制系统设计
舵机控制系统主要由算法控制器、PWM驱动器、直流无刷伺服舵机、减速传动机构和反馈电位器组成[6],搭建位置闭环控制,如图1所示。

图1 舵机系统闭环控制结构
电动舵机的作用是将电能转化为机械能,其数学模型可以描述其动态特性[7]。对直流无刷舵机进行数学建模,得到其系统动态模型结构如图2所示。

图2 直流无刷舵机动态模型结构
图2中,Ua为理想位置指令信号;r1为电枢电阻;L为电枢电感;KT为电机转矩系数;JM为电机转子、舵片以及减速传动机构折算到电机转轴上的转动惯量;KE为反电动势系数;TL为负载和外部扰动折算到电机转轴上的力矩[8]。
可以得到伺服舵机的传递函数为:

(1)
在空载条件下(TL=0),伺服电机的传递函数表达式为:
(2)
由于无刷电机转速较高,但输出力矩较小,需要通过减速传动机构配合使用,其传递函数为常数,如式(3)所示:
(3)
其中,θm为舵机轴旋转度数,单位是弧度,由于常用角度δ表示,则有:
(4)
2 改进模糊神经网络PID控制器设计
2.1 模糊控制原理及过程
模糊控制是以模糊集合论、模糊语言及模糊推理为理论基础,并基于实际操作经验,采用自然语言描述控制策略,或通过大量的实验总结出控制规则,用计算机予以实现的智能控制算法。在模糊控制中,不必精确知道被控对象的数学模型,只需在建立好的知识库中搜索所需的状态量满足的模糊规则,即可得到满足条件的输出量。

图3 模糊控制结构框图
模糊控制基本结构框架如图3所示,具体过程主要包括以下4部分:
1)模糊化。将输入的精确量变换到论域的输入量进行模糊处理,转化成相应模糊量并用模糊集合来表示。
2)知识库。由数据库和模糊规则库组成。其中数据库主要包括各个模糊变量的隶属函数、量化因子以及模糊分割数等;规则库包括用模糊语言变量表示的一系列模糊控制规则。
3)模糊推理。该部分是模糊控制的核心,模拟人类的推理能力,基于模糊规则推理得到输出量的模糊变量。
4)清晰化。该部分作用是将模糊推理得到的控制量变换成实际的清晰量,作用于被控对象。
由此可见模糊控制具有较强的推理能力,但缺乏自学习能力,将神经网络的自学习能力赋予模糊控制器,即可使控制器兼具2种控制器的优点,达到更好的控制效果。
2.2 模糊神经网络PID控制器结构
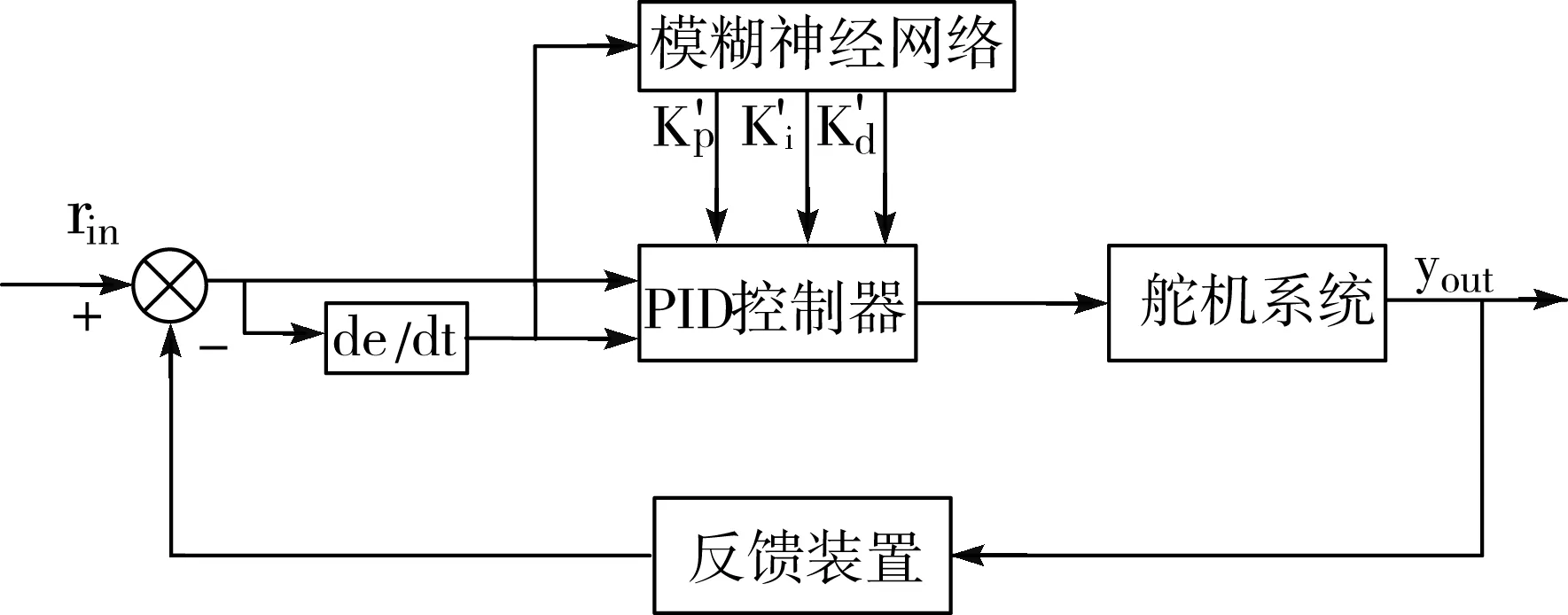
图4 模糊神经网络PID控制器结构
将PID控制器与模糊RBF神经网络相结合,利用PID控制器进行参数Kp,Ki和Kd的预整定,再通过模糊RBF神经网络按照Delta监督学习规则,自学习修正PID控制器中的参数[9],最终使系统达到最优控制。本文所设计的模糊神经网络PID控制器结构如图4所示。
模糊神经网络PID控制器的输入量为位置误差e和误差的变化率ec,输出量为PID控制器的修正参数[10],其中ec(k)=e(k)-e(k-1),该模糊神经网络将神经网络的自学习能力应用于模糊控制中,通过学习机制对网络的权值、中心矢量和基宽参数进行修正操作,获得最适合系统的参数调整值,记录得到的输出控制量[11]。
2.3 控制器的工作原理
本文设计的是基于RBF网络的模糊神经网络PID控制器,网络结构与多层前向网络类似,具有输入层、隐含层和输出层,层与层的节点之间通过权值连接。通过神经网络结构来表示模糊逻辑系统,每一层神经网络分别对应着模糊逻辑系统的隶属度函数或推理规则,传统的模糊神经网络一般为5层结构,如果分析系统较为复杂,则导致网络结构非常庞大,过于复杂的运算会使得控制效果降低。针对上述原理和现象,本文设计的模糊RBF神经网络结构分为4层,即输入层、模糊化层、模糊规则层和清晰化层[12],该设计使模糊神经网络结构更为简单,运算量大大减少,网络结构如图5所示。

图5 模糊神经网络结构
模糊神经网络各层介绍如下:

(5)
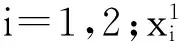
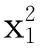
(6)
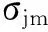
3)模糊规则层。该层的每个神经元节点代表一条模糊控制规则,通过与模糊化层节点的连接来完成模糊控制规则的匹配,此处采用“乘”算子来实现模糊“与”运算,从而得到每条控制规则的适应度,并将输出值进行归一化处理,此层共有49个模糊规则,通过式(7)和式(8)完成模糊规则的推理[14]。
(7)
(8)

4)清晰化层。该层的作用是实现反模糊化计算,将模糊量转变为应用于实际控制系统中的清晰量。
(9)
(10)
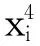
本设计采用增量式PID控制算法,其控制规律为:
u(k)=u(k-1)+Δu(k)
(11)
Δu(k)=kpxc(1)+kixc(2)+kdxc(3)
(12)
其中,
xc(1)=e(k)-e(k-1)
(13)
xc(2)=e(k)
(14)
xc(3)=e(k)-2e(k-1)+e(k-2)
(15)
2.4 改进模糊神经网络学习算法
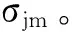
2.4.1 自组织学习阶段
自组织学习过程是对所有样本的输入进行聚类,求得各隐含层节点的模糊神经网络的均值和标准差[15]。这里采用K均值聚类算法调整中心向量,此算法将训练样本集中的输入向量分为若干族,在每个数据族内找出一个径向基函数中心向量,使得该族内各样本向量距该族中心的距离最小[16]。算法步骤如下:
1)计算距离(欧氏距离)并求出最小距离的节点。
dmin(k)=dr(k)=min {‖x(k)-cjm(k-1)‖}
(16)
其中,k为样本序号;r为中心向量与输入样本距离最近的隐节点序号;d为欧式距离。初始cjm(0)是一个比较小的随机数。
2)调整中心向量。
(17)
其中,β(k)是一个逐次递减的标量学习速率,cr(k)是距离输入样本最近的隐节点中心向量。
3)判定聚类质量。对于全部样本反复进行上述步骤,直至满足以下条件,则聚类结束。
∑‖x(k)-cjm(k)‖2ε
(18)
其中,ε为判定停止计算的阈值。
(19)
其中,m为重叠系数。
2.4.2 有教师学习阶段
当均值和标准差确定以后,训练模糊规则层与清晰化层之间的权系数,由上可知,它是一个线性方程组,则求权值就成为线性优化问题。因此,不存在局部极小值问题,有唯一确定的解,即全局最小点。连接权值wij的学习算法为:
wij(k+1)=wij(k)+η[rin(k)-yout(k)]F(x)/uTu
(20)
其中,η为学习速率;rin(k)和yout(k)分别表示第k个输出向量的期望值和实际值;F(x)为高斯函数;u为输入向量。由于输入向量u中只有少量几个元素为1,其余均为0,因此需要调整的连接权系数大大减少,这一特点加快了RBF神经网络的学习速率。
3 系统仿真实验
根据无刷直流舵机的数学模型,利用MATLAB软件中的Simulink仿真模块对该舵机控制系统进行仿真分析,验证模糊神经网络PID控制算法的控制效果。所构建的舵机控制系统仿真模型是三闭环控制结构,由内到外分别是电流环、速度环和位置环。电流环采用带有输出限幅的PI调节器,对舵机驱动器进行过流保护[17];速度环采用带有饱和特性的PID调节器;而位置环则采用本文所提出的模糊神经网络PID控制器[18],直流无刷舵机控制系统仿真模型如图6所示。

图6 舵机控制系统仿真模型
本次实验中,直流无刷舵机选用瑞士MAXON公司的某型号直流无刷电机,该电机参数如表1所示。
表1 直流无刷舵机参数表

额定电压/V24转动惯量/g·cm262.3相间电阻/Ω0.436额定转速/r·min-18050反电动势系数/Vs·rad-10.036减速机构传动比225额定功率/W90转矩系数/mN·m·A-117.6相间电感/mH0.064
分别将阶跃信号和正弦跟踪信号输入到上述仿真模型中,采用改进算法对其进行仿真分析,对比PID控制器,模糊PID控制器和模糊神经网络PID控制器的控制效果,如图7~图8所示。
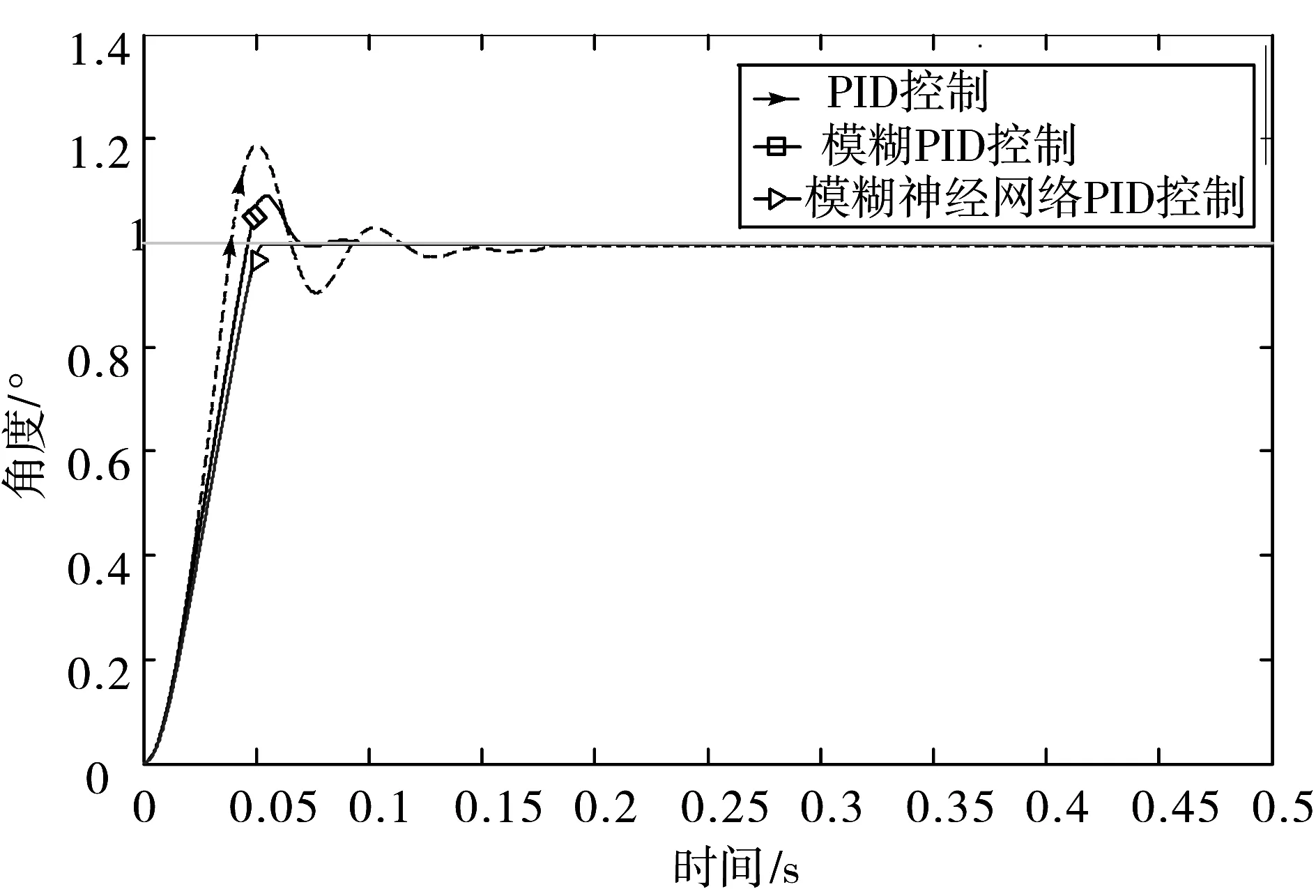
图7 单位阶跃响应仿真对比曲线
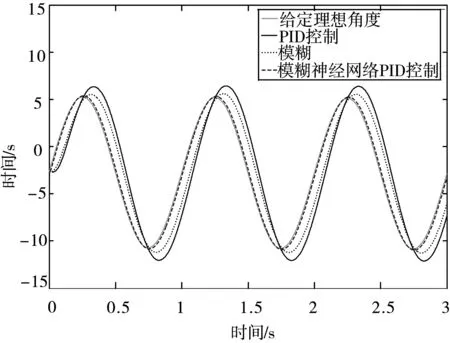
图8 正弦跟踪响应仿真对比曲线
4 结果与分析
分析仿真得到的结果与各个控制器的性能指标,整理得到表2。
表2 各控制器的性能指标
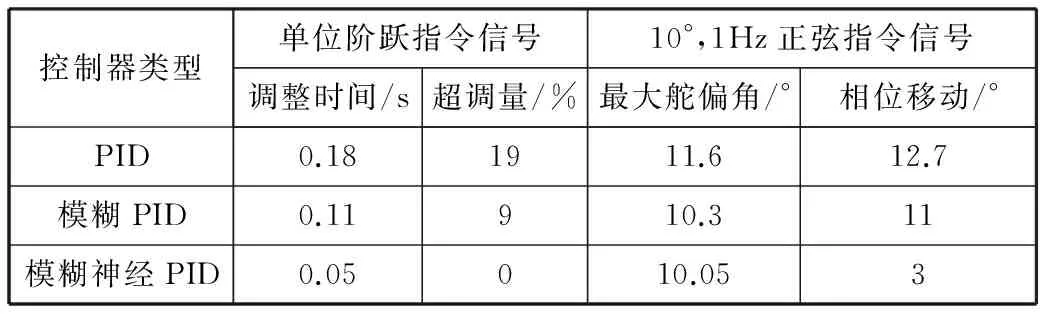
控制器类型单位阶跃指令信号10°,1Hz正弦指令信号调整时间/s超调量/%最大舵偏角/°相位移动/°PID0.181911.612.7模糊PID0.11910.311模糊神经PID0.05010.053
综合仿真结果图与性能指标表分析,在输入1°的阶跃信号时,传统的PID控制器因不具有自整定能力,超调量高达19%,到达稳态的调整时间是0.18 s;模糊PID控制器的控制效果有所提高,超调量是9%,到达稳态的调整时间是0.11 s,但是在实际操作过程中需要调整的参数较多,工作量较大。本文所设计的模糊神经网络PID控制器具有在线学习的能力,基本无超调,到达稳态的调整时间为0.05 s,可以证明,该模糊神经网络PID控制器在应用于无刷直流舵机位置环控制时,响应速度较另外2种控制器有明显的优势,表明本文提出的分阶段学习算法令该模糊神经网络的学习效率有所提升。
在输入指令为10°且1Hz的正弦信号时,PID控制器下的无刷直流舵机系统实际最大舵偏角为11.6°,相位移动约为12.7°;模糊PID控制器下实际最大舵偏角为10.3°,相位移动约为11°;而在模糊神经网络PID位置环控制器下,舵机系统实际最大舵偏角为10.05°,相位移动约为3°,由此可知,该控制算法稳态精度较高,在跟踪系统性能方面有显著性提升。
5 结束语
本文提出了一种改进的模糊神经网络PID控制算法,该算法采用自组织学习阶段和有教师学习阶段的分阶段学习方式。设计直流无刷电动舵机控制系统,并将该控制器应用于舵机系统位置环控制过程。通过在MATLAB中建立仿真模型进行实验,可发现该控制器对阶跃响应更加迅速,到达稳态的调整时间短,基本无超调;对最大舵偏角指令能更准确地执行,相位移动小。可以说明本文所设计的模糊神经网络PID控制器,在非线性及时变的复杂系统中具有更为优良的控制效果。
将该模糊神经网络PID控制算法应用到可编程逻辑控制器中,搭建舵机控制系统,可以进一步改进舵机控制系统的动态性能,同时也体现了该控制器的工程应用价值。
[1] 崔业兵,陈雄,蒋魏,等. 自适应模糊神经控制器的电动舵机控制[J]. 微特电机, 2013,41(12):57-60.
[2] 和江,彭舒钰,侯文. 模糊神经网络PID在数字舵机控制中的应用[J]. 计算机测量与控制, 2016,24(10):79-81.
[3] 吴娟,张家盛,康光会. 舵机系统动刚度的分析研究[J]. 科学技术与工程, 2008,8(4):1124-1128.
[4] 武彬,沈幼庭. 一种模糊神经网络的改进学习算法[J]. 清华大学学报(自然科学版), 1999,39(10):31-34.
[5] 廉美琳,陈泽宇,顾志华,等. 基于模糊神经网络整定的汽油机怠速PID控制[J]. 南京师范大学学报(工程技术版), 2012,12(4):6-10.
[6] 王晓洲. 基于永磁直流无刷电机的电动飞行器舵系统的设计[D]. 哈尔滨:哈尔滨工业大学, 2009.
[7] 崔业兵. 制导火箭弹固定鸭式舵机滚转控制技术研究[D]. 南京:南京理工大学, 2014.
[8] 李柱勇. 双余度电动舵机系统的研究与设计[D]. 南京:南京航空航天大学, 2010.
[9] 胥良,郭林,梁亚,等. 基于模糊RBF神经网络的智能PID控制[J]. 工业仪表与自动化装置, 2015(6):67-69.
[10] 张桂兰. 模糊神经网络在船舶动力定位系统中的应用[D]. 镇江:江苏科技大学, 2005.
[11] 和江,文建刚,侯文. 基于模糊神经网络PID算法的舵机控制与仿真[J]. 中北大学学报(自然科学版), 2016,37(2):150-156.
[12] 吴新生. 纸浆浓度的模糊神经网络自适应PID控制[J]. 计算机测量与控制, 2013,21(11):2969-2971.
[13] 王印松,刘武林. 一种PID型模糊神经网络控制器[J]. 系统仿真学报, 2003,15(3):389-392.
[14] 苏永利. 基于加权模糊规则的自适应神经—模糊推理[D]. 保定:河北大学, 2005.
[15] 张元,周长省. 模糊神经网络PID在电动舵机控制中的应用[J]. 计算机仿真, 2012,29(5):77-80.
[16] 孟莎莎,孙宝华,杨辉,等. 径向基神经网络辨识非线性系统的改进算法[J]. 华东交通大学学报, 2009,26(3):37-41.
[17] 张梦,乔晓君,冯殿震. 基于LuGre摩擦模型的鱼雷舵机伺服控制系统自适应反演滑模控制[J]. 舰船电子工程, 2016,36(4):54-57.
[18] 王宏. 无刷直流电动机控制系统的研究与设计[D]. 南京:南京理工大学, 2003.
