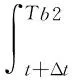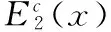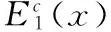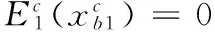运营滞后与信用担保互换下的项目投资决策模型
2018-03-29罗鹏飞杨招军
甘 柳,罗鹏飞,杨招军
(1.湖南大学金融与统计学院,湖南 长沙 410079;2.湖南商学院财政金融学院,湖南 长沙 410205;3.南方科技大学金融系, 广东 深圳 518055)
1 引言
实物期权的研究始于McDonald和Siegel[1],而Dixit和Pindyck[2]对实物期权的全面研究形成了探究不可逆投资的标准方法。随后广大学者从资本市场摩擦、债务融资、外部融资成本以及管理者决策等角度来逐步改变或放松标准实物期权模型的假设条件,以更真实刻画不确定市场环境中的项目投资决策。例如Childs等[3]和Mauer等[4]在实物期权框架下引入债务融资,基于股东与债权人代理冲突,研究企业投资和融资的相互影响;Shibata和Nishihara[5-7]进一步引入外部债务融资约束,分析债务融资约束对企业投资与融资行为的影响;Andrikopoulos[8]和Hori等[9]在实物期权框架下引入管理者,研究当管理者与股东决策不一致时,企业投资与融资的相互影响;另外,国内学者也对实物期权理论进行了多方位的拓展[10-14]。然而,以上文献都没有考虑项目面临运营滞后的现实问题,即项目投资完成与正式运营之间存在时滞。例如土地建设项目可能因为审批而延迟,根据相关数据,发电厂项目或机场建设项目从进入投资到运营可能会花费6到10年时间,煤矿项目从投资到运营也需要5到6年时间来完成,等等。因此,作为一般理论扩展,探讨运营滞后下的项目投资问题具有实际价值。
基于此,Alvarez和Keppo[15]构建实物期权框架下交付滞后的投资模型,研究企业纯股权融资情形的不确定性投资问题,发现投资的不确定性会导致延迟投资,Sarkar和Zhang Chuanqian[16]以及Agliardi和Koussis[17]进一步扩展这一模型,发现投资不确定性和滞后时间都会导致延迟投资。Sarkar和Zhang Chuanqian[18]首次在项目可以债务融资的假定下,研究运营滞后对企业投资和融资决策的影响,发现滞后时间对投资决策的影响取决于企业的杠杆率。这些理论文献从不同角度探讨了运营滞后对企业投资决策的影响,然而,这些模型或者没有考虑债务融资,或者假设无摩擦的信用市场。事实上,由于宏观政策与市场环境、金融服务结构与企业信用质量等因素的影响,企业家外部融资会面临一定债务融资约束[19-20],显然债务融资约束会对企业投资决策会产生重大影响。
从债务融资约束的角度,杨兆廷和李吉栋[19]介绍了“担保换期权”,并认为这一信用工具缓解了中小企业融资约束。盛世杰等[20]认为引入政策性担保机构是解决中小企业融资难问题的有效方法,并从情景分析和盈亏平衡点测算等方面对政策性担保机构为中小企业贷款提供担保进行了可行性分析。另一方面,Yang Zhaojun和Zhang Hai[21]给出信用担保互换的定量分析,论证信用担保互换的使用不仅可以降低企业的破产边界而且提高了企业的总价值。Zhang Chunhong和Yang Zhaojun[22]计算了动态模型下信用担保互换的公平价格,分析不同风险厌恶程度下企业家会选择何种担保方式进行债务融资。Wang Huamao等[23]基于非完备市场模型分析了信用担保互换。Xiang Hua和Yang Zhaojun[24]分析信用担保互换对企业投资的影响。Gan Liu等[25]构建基于协商的博弈模型,分析企业家议价能力对信用担保互换的影响。
与以上文献相区别,本文的贡献体现在如下三个方面:第一,构建基于运营滞后和信用担保互换的实物期权模型,采用两阶段投资方式来刻画运营滞后,并考虑企业家在担保公司介入下的投资决策行为,拓展了实物期权的研究;第二,探索企业家与担保公司签订信用担保互换协议对企业家投资决策影响的内在机制,进而从缓减债务融资约束的视角为使用信用担保互换提供新的理论解释;第三,给出了企业家两阶段融资的股权转让数量的计算公式,得到了信用担保互换模式下的企业家最优投资决策,为缓解中小企业融资约束提供理论指导。
2 模型框架与假设
2.1 项目收益流
参考经典实物期权模型[2],假定企业家拥有一个不可逆的项目投资机会,投资时需要支付总成本I。由于面临运营滞后,投资成本的支付方式与传统一次性支付不同,需分成两个阶段,每个阶段支付一定比例的投资成本(具体见2.2节)。
项目的税前收益流{xt,t≥0}服从如下几何布朗运动:
dxt=μxtdt+σxtdWt,x0给定
(1)
其中μ与σ为常数,分别表示项目现金流的期望增长率和波动率,且μ 根据Goldstein等[26]税收结构:设个人所得税率为τi,有效分红税率为τd,企业所得税为τc,于是有效税率τf=1-(1-τc)(1-τd)。 参考Sarkar和Zhang Chuanqian[18]及Margsiri等[27],利用外生参数来刻画运营滞后的期望时间,采用两阶段投资方式来刻画运营滞后。第一阶段企业家会通过实物期权方法确定一个最优投资时机,在这个时间点上企业家进入项目并支付投资成本θI(0≤θ≤1),由于运营滞后效应,企业家在第一阶段投入之后并不产生营业收入,经过一段时间后企业家进入第二阶段的投资,第二个阶段企业家支付投资成本为(1-θ)I,第二次投资之后项目进入正常经营阶段并产生营业收入。 为了刻画运营的滞后时间,需要明确项目的投资时机,第一阶段投资时机(停时)记为T1,第二阶段投资时机记为T2,由模型的Markov性质可知,存在投资触发水平xi,使得T1=inf{t|xt≥xi},并且进一步利用参数β来刻画T2,将第二阶段投资触发水平记为βxi,β>1以保证第二阶段投资时机在第一段之后,于是T2=inf{t|xt≥βxi}。第一阶段投资时刻与第二阶段投资时刻的差就是运营时滞,将这个时间差记为L,显然L是一个随机变量。利用Margsiri等[27]的方法,容易计算出L的期望值如下: (2) 下文称E(L)为运营时滞,β越大则L的期望值越大。另外假定L与投资时机独立。 进行项目投资时,假定企业家可以通过担保公司的信用担保来实现债务融资,而担保公司为了获取回报,需要与企业家签订信用担保换互换契约。在该协议中,贷方把钱借给企业家后,得到固定券息c(表示投资的两个阶段的券息,下文会分开表述),而一旦企业家违约,担保公司家为企业家代偿全部剩余本金和利息,将这个代偿价值记为Dguar(x),支付代偿部分的税率与利息税率一致,均为τi。假定贷方利益可以得到充分保护,于是Dguar(x)满足以下等式: (1-τi)Dguar(x)=(1-τi)c/r-D(x) (3) 其中D(x)为风险债务价值,(1-τi)c/r为无风险债务税后价值。式(3)的含义:在担保公司承担风险后,对于贷方而言,债务是无风险的,于是担保公司承代偿的价值是无风险债务价值和风险债务价值的差。 据互换协议,担保公司代偿值Dguar(x)需要通过企业家股权份额来弥补(企业家获得担保需要付出的成本),即担保公司收入与承担的风险需相等,将股权份额比重记为φ(下文称之为担保成本),担保公司实际代偿价值为(1-τf)Dguar(x),于是: φE(x)=(1-τf)Dguar(x) (4) 其中,E(x)为项目总股权价值。 式(3)和式(4)刻画了在债务融资约束下,企业家为获取信用担保所付出的成本。 由于项目两阶段投资的特点,需利用倒向递推的方法来计算各未定权益价值。首先计算项目第二阶段投资后的股权价值与债务价值,然后计算第二阶段投资前第一阶段投资后的股权价值与债务价值,最后计算第一阶段投资前的期权价值。为叙述方便,本文将第二阶段投资后的证券价值用下标2标示,第二阶段投资前第一阶段投资后用下标1标示,第一阶段投资前用下标0标示。 在第二阶段投资后且企业家没有签订信用担保协议,项目的税后收益流为(1-τf)(xt-c1-c2),其中c1为支付给第一阶段债权人的券息,c2为支付给第二阶段债权人的券息。根据资产定价理论,第二阶段投资后企业家股权价值E2(x)为: (5) 其中,Tb2为企业家决定的最优破产时机,定义为Tb2=inf{t|xb2≥xt},xb2为对应的最优破产触发水平,即企业家通过决定最优的破产时机来最大化其股权价值。 同理,无信用担保协议下,第二阶段融资的债务价值D2(x)为: (6) 对式(5)和式(6)利用动态规划方法,可求得股权和债务价值,并总结为如下引理。 引理1 企业家没有签订信用担保协议,在项目第二阶段投资后,企业家的股权价值为: (7) 第二阶段融资的债务价值为: (8) 第一阶段融资的债务的价值为: (9) 证明:见附录A。 引理1的结果类似于Leland[28]的相关结论,债务融资会带来税收上获利同时也会带来破产风险。股权价值E2(x)的含义:第一项为不考虑破产的税后股权净价值,其中(1-τf)x/(r-μ)为税后纯股权价值(见附录(A9)),(1-τf)(c1+c2)/r为支付债务价值,第二项为破产的时刻股权值折算到当前的价值,(1-τf)[xb2/(r-μ)-(c1+c2)/r]为破产时刻的股权价值,而(x/xb2)γ2为折现因子。于是企业家当前的股权价值为项目总价值减去债务价值,再减去项目破产损失价值。D2(x)与D12(x)的解释与之类似,但需要注意,债权人是两部分,故破产时刻的项目价值(1-α)(1-τf)xb2/(r-μ)需根据债权人所占比例来分,c2/(c1+c2)为第二阶段债权人所占比重。 接下来考虑项目第一阶段投资后第二阶段投资前的情形,在这个阶段,企业家没有营业收入,但是要支付券息,于是其收益流为-(1-τf)c1。担保公司会考虑到第二阶段信用担保协议的签订,股权价值为: (10) 其中Tb1为最优破产时机,根据前文分析便有Tb1=inf{t|xb1≥xt},xb1为对应的最优破产触发水平,1T2 同理,无信用担保协议下,第一阶段投资后第二阶段投资前的债券价值D1(x)为: e-r(Tb1∧T2-t)[1T2 (1-α)V1(xb1)]} (11) 其中,D12(x)为第一阶段发行的债务在第二阶 段的价值(式(9)给出),V1(xb1)为第一阶段投资后第二阶段投资前,破产时的项目价值(附录(B6)给出)。式(11)的含义:在第一阶段投资后,债权人得到券息支付,直到项目破产或进入第二阶段,若破产则债权人接管项目得到价值为(1-α)V1(xb1),若进入第二阶段投资,则债务价值为D12(βxi)。 引理2 第一阶段融资无信用担保,但第二阶段融资采用信用担保。则在第一阶段投资后第二阶段投资前企业家的股权价值为: E1(x)=Axγ1-Bxγ2-(1-τf)c1/r (12) 债务价值D1(x)为: D1(x)=Cxγ1-Dxγ2+(1-τi)c1/r (13) 最优破产触发水平xb1满足代数方程: (14) 证明:见附录B。 为解释引理2,先给出如下折现因子: (15) (16) 显然,当前时刻为破产时刻x=xb1时,有Δd(xb1;xb1,βxi)=1及Δi(xb1;xb1,βxi)=0,当前时刻为第二阶段投资时刻x=βxi时,有Δd(βxi;xb1,βxi)=0及Δi(βxi;xb1,βxi)=1。于是,式(12)可以重新写为, (17) 式(17)的第一项-(1-τf)c1/r为不考虑破产及第二次投资,企业家支付券息在当前时刻的价值,第二项为破产时刻企业家的净价值-(1-τf)c1/r乘以折现因子Δd(x;xb1,βxi),第三项为进行第二次投资时企业家的净价值(1-φ2)E2(βxi)-(1-θ)I+(1-τi)c2/r乘以折现因子Δi(x;xb1,βxi)。于是,E1(x)为在这个阶段支付出去的债务价值,减去破产时刻支付的价值,再加上在第二次投资时刻得到的总价值。同理可以解释式(13)。 最后,考虑企业家的担保成本。担保成本的计算方式在2.3节已经给出,其联立方程总结为如下定理。 定理1 第一阶段融资的担保成本φ1与第二阶段融资的担保成本φ2满足如下联立方程: (18) 其中,E1(x)、E2(x)、D1(x)以及D2(x)分别由式(7)、式(8)、式(12)和式(13)给出。 证明:由公平担保原则式(3)和式(4)可得。 至此,给出了两个阶段签订信用担保互换协议下的担保成本满足的代数方程。 信用担保协议的签订会影响到企业家决策行为,故需要重新评估证券价值。签订担保协议的情形下,项目第二阶段投资后,由于两次分出去了股权,企业家得到税后收益流(1-τf)(1-φ1)(1-φ2)(xt-c1-c2),其中φ1与φ2由定理1给出。为与上节相区别,本节采用上标c表示签订信用担保协议的情形,于是有如下引理: (19) 其中,此阶段的最优破产触发水平为 (20) 第一阶段投资后,且第二阶段投资前企业家的股权价值为: (21) (22) 证明:见附录C。 引理3的经济含义类似于引理2。 最后计算第一阶段投资前企业家的期权价值F0(x),在第一段投资前企业家也没有收益流,于是有如下定理: 定理2第一阶段投资前企业家期权价值为: (23) 其中M和N由引理3给出。 证明:见附录D。 有了定理2做准备,企业家投资决策的优化问题可以写成如下形式: (24) 式(24)的经济含义:首先,企业家通过最大化0时刻期权价值做出最佳投资决策,由此目标函数。其次,约束条件的第一个等式表示企业家在第一阶段面临债务融资约束,签订信用担保互换支付成本所满足的代数方程。第二阶段签订担保协议时会考虑到第一阶段企业家所支付的担保成本,而运营时滞通过参数β对企业家的投资决策形成约束。约束条件的第二个等式表示企业家在第二阶段面临债务融资约束,签订信用担保互换支付成本所满足的代数方程。约束条件的第三个等式表示企业家在第一阶段和第二阶段支付的信用担保成本通过破产触发水平联系起来。于是式(24)的约束条件一方面刻画了企业家在面临融资时所需要付出的成本,另一面刻画了企业家项目投资过程中的运营滞后现象。 优化问题式(24)需要借助数值方法来求解。参考文献[18]和[25]在数值计算部分选取的参数,本节的基本模型参数设定为:无风险利率r=0.06,收益流的期望增长率μ=0.04,收益流波动率σ=0.2,第一阶段的投资比重θ=0.3,破产损失率α=0.35,有效税率τf=0.35,所得税为τi=0.05,初始现金流x0=1,总投资成本I=20,运营时滞为E(L)=5(β=1.1052)。另外,对于项目融资,融资缺口多大就融资多少,故债务券息外生给定c1=c2=1。 本小节考虑运营时滞对企业家的投资决策、杠杆率以及担保成本的影响。图1a显示,最优投资触发水平随着运营时滞的增加而递减,即运营滞后的期望时间越长,企业家越会提前投资。由于处于第一阶段投资后及第二阶段投资之间时,企业家没有营业收入,却需要支付第一阶段融资的券息,于是当其它条件不变,随着运营时滞增加,企业家股权价值是降低的。此时由于项目的无风险债务价值不变,于是项目融资的杠杆率会升高,从图1b所示杠杆率的变化可以证实这一点。实物期权的一般结论表明,随杠杆率增加,企业家投资会提前。因此,从图1看出,运营时滞通过提高项目融资的杠杆率,而使得企业家决定的投资时机提前。另一方面,随着项目风险(波动率)的增加,项目的融资杠杆率降低,而投资时机是延后,这与已有结论一致。 图2给出两个投资阶段融资的担保成本随运营时滞的变化。从图2a可以看出,随运营时滞增加,第一阶段担保成本φ1单调递增,但注意到图2a中的两条线出现了交叉,即运营时滞为在E(L)=8.1之前,φ1随项目风险的增加而增加,但在8.1之后,随项目风险的增加而减少。这由两个因素引起的,首先,运营时滞增大会降低第一阶段的股权价值,其次,项目波动率增加会增加项目的股权价值,在运营时滞较低时,第一因素占主导地位,而运营时滞较高时,第二个因素占主导地位。图2b显示,第二阶段的担保成本φ2的随着运营时滞的增加而递减,且波动率提高会增加第二阶段的担保成本,因为运营时滞会使得第二阶段的股权和风险债务价值增加,而波动率使得股权价值增加但导致风险债务价值降低。 图1a 投资触发点随运营时滞变化关系 图1b 杠杆率随运营时滞变化关系 图2a 担保成本φ1随运营时滞变化关系 图2b 担保成本φ2随运营时滞变化关系 本小节考虑投资比重对投资决策、杠杆率以及担保成本的影响。图3a表明最优投资触发水平随着第一阶段投资比重θ的增加呈U型。一方面,随着θ增加,企业家股权价值会增加,从图3b可以看出,杆杆率会随着θ增加而递减,于是这一因素会导致企业家提前投资,另一方面,在同等滞后水平下(E(L)=5),随着第一阶段投资成本数量的增加,企业家的投资时机会延迟。在θ较小时,第一个方面的因素占主导地位,在θ较大时,第二个方面的因素占主导地位,于是最优投资触发水平随着第一阶段投资比重θ的增加呈U型关系。 从图4a可以看出,随θ的增加,第一阶段担保成本φ1单调递减,且波动率对其的影响,在不同阶段也不一样。虽然θ增加以及波动率增加都会导致股权价值增加,但是θ增加以及波动率对风险债务价值影响是不同的,θ增加会导致风险债务价值增加,而波动率增加会导致风险债务价值减少,这两方面的影响导致了图4a所示结论。图4b显示,第二阶段的担保成本φ2随着θ增加而先增后减,且波动率提高会增加担保成本,这是由于θ的增加导致第二阶段投资后的股权价值和风险债务价值呈U型变化。 图3a 投资触发点运投资比重变化关系 图3b 杠杆率随运投资比重变化关系 图4a 担保成本φ1随投资比重变化关系 图4b 担保成本φ2随投资比重化关系 本小节考虑两个阶段的券息对投资决策、破产水平以及担保成本的影响。图5a表明券息的增加都会导致企业家提前投资,其原因是明显的,券息增加提高了杠杆率,高杠杆会导致企业家提前投资。另一方面,图5b可以看出,更多的债务水平会导致企业家提高第一阶段的破产水平。 图5a 投资触发点随券息变化关系 图5b 破产触发点随券息变化关系 图6表明券息增加导致债务价值增加,此时担保公司面临的风险也增加,因此两个阶段的担保成本都随券息增加而增加,由于两个阶段担保协议的相互影响,两个阶段的券息会对担保成本造成相互影响。 图6a 担保成本φ1随券息变化关系 图6b 担保成本φ2随券息化关系 很多学者认为解决中小企业融资难的问题,关键在于解决担保问题,但占企业总数99%以上的中小企业难以通过通常的方式获得债务融资。在现实中有许多创业企业家尤其是高新科技类企业家拥有不错的项目投资机会,但由于信息不对称,在筹集启动资金时往往面临融资约束。而担保公司凭其雄厚的经济实力提供担保,可以实现创业企业、担保公司和银行的多赢局面。本文基于经典的实物期权模型框架,结合运营滞后理论和信用担保,构建了企业家项目投资决策模型,考虑企业家的最优投资水平、项目杠杆率、破产选择以及担保成本问题。通过数值计算和比较静态分析,揭示外部环境和企业自身因素的变化所带来的投资决策和担保成本的变化。外部运营时滞导致企业家提前投资,同时通过影响股权价值和风险债务价值使第一阶段的担保成本升高而第二阶段的担保成本降低。而且,投资比重以及企业家的融资缺口会对投资水平、破产水平以及担保成本会产生显著影响。 最后指出,本文进一步研究包括两个方面:首先,企业发展需要不断地扩展投资规模,因此,建立动态投资模型来研究企业的成长规律是有意义的;其次,企业家同时还面临不可分散的非系统性风险,结合这一因素的研究也是重要的拓展。 附录A 引理1的证明。 值函数式(5)与变量x有关,而x的微分方程由式(1)给出。根据贝尔曼原理有 (A1) (A2) 令Δt→0,并将(A2)带入(A1)则有 (A3) 将(A3)整理化简得E2(x)满足: (1-τf)(x-c1-c2)=0 (A4) 并满足如下边界条件 (A5) 其中,(A5)第一个式子表明收益流很大,股权价值为无违约风险下相应价值,第二个式子是价值匹配,在企业破产时股权无价值。于是(A4)解为 E2(x)=A1xγ1+A2xγ2+ (A6) 其中A1和A2为常数,对(A6)利用边界条件(A5)可以得到式(7)。破产水平由光滑粘贴条件∂E2(x)/∂x|x=xb2=0给出: xb2=γ2(r-μ)(c1+c2)/[(γ2-1)r] (A7) (A8) 其中,(A8)中第一个式子表明收益流很大,债券价值为无违约风险下相应的价值,第二个式子是价值匹配,破产时债权人接手项目获得剩余价值c2(1-α)V2(xb2)/(c1+c2),V2(x)为第二阶段投资后的纯股权价值: (A9) 最后,不难得到D2(x)的通解为 D2(x)=C1xγ1+C2xγ2+(1-τ)c2/r (A10) 其中C1和C2为常数,(A10)用边界条件(A8)可得式(8),同理可得式(9)。证毕 附录B 引理2的证明。 利用引理1的证明方法,式(10)满足: (1-τf)c1=0 (B1) 及边界条件: E1(βxi)=(1-φ2)E2(βxi)-(1-θ)I+(1- τi)c2/r,E1(xb1)=0,和∂E1(x)/∂x|x=xb1=0 (B2) 其中,(B2)中第一个式子为股权价值在第二阶段投资时的价值匹配条件,E2(x)由式(7)给出,第二个式子表明,当企业家宣布破产时,股权价值为0。于是(B2)的通解为: E1(x)=Axγ1-Bxγ2-(1-τf)c1/r (B3) 其中A和B为常数,通过边界条件(B2)可以得到A和B。对式(12)运用(B2)的第三个边界条件可以计算得到式(14)。 (B4) 及边界条件: D1(βxi)=D12(βxi),D1(xb1)=(1-α)V1(xb1) (B5) (B6) 最后,(B4)的解为: D1(x)=Cxγ1-Dxγ2+(1-τi)c1/r (B7) 其中C和D为常数,对(B7)利用边界条件(B5)可以得到式(13)。证毕 附录C 引理3的证明。 (1-τf)(1-φ1)(1-φ2)(x-c1-c2)=0 (C1) 及边界条件 (C2) 根据(C1)的通解和边界条件(C2),可以得到式(19)和式(20)。 (1-τf)(1-φ1)c1=0 (C3) 及边界条件: (C4) 根据(C3)的通解和边界条件(C4),可以得到式(21),对式(21)运用(C4)的第三个边界条件可以计算得到式(22)。证毕 附录D 定理2的证明。 在第一阶段投资前企业家没收益流,于是期权价值F0(x)满足如下微分方程: (D1) 及边界条件 F0(0)=0 (D2) 其中,(D2)中第一个式子为期权价值在第一阶段投资时的价值匹配条件,第二个式子表明,当收益流为0时,期权没有价值。于是,利用(D1)的通解以及边界条件(D2)可以得到式(23)。证毕 [1] Mcdonald R, Siegel D. The value of waiting to invest[J]. Quarterly Journal of Economics, 1986, 101(4): 707-727. [2] DixitA K, Pindyck R. Investment under uncertainty[M]. Princeton, NY: Princeton University Press, 1994. [3] Childs P D, Mauer D C, Ott S H. Interactions ofcorporate financing and investment decisions: the effects of agency conflicts[J]. Journal of Financial Economics, 2005, 76(3): 667-690. [4] Mauer D C, Sarkar S. Real options, agency conflicts, and optimal capital structure[J]. Journal of Banking and Finance, 2005, 29(6): 1405-1428. [5] Shibata T, Nishihara M. Investmenttiming under debt issuance constraint[J]. Journal of Banking and Finance, 2012, 36(4): 981-991. [6] Shibata T, Nishihara M. Investmenttiming, debt structure, and financing constraints[J]. European Journal of Operational Research, 2015, 241(2): 513-526. [7] Shibata T, Nishihara M. Investment-based financing constraints and debt renegotiation[J]. Journal of Banking and Finance, 2015, 51(2): 79-92. [8] Andrikopoulos A. Irreversible investment, managerial discretion and optimal capital structure [J]. Journal of Banking and Finance,2009, 33(4): 709-718. [9] Hori K, Osano H. Investment timing decisions of managers under endogenous contracts[J]. Journal of Corporate Finance, 2014, 29: 607-627. [10] 杨金强, 杨招军. 部分信息下实物期权的定价和风险对冲[J].中国管理科学, 2011, 19(4): 9-16. [11] 谷晓燕. 基于实物期权的研发项目动态投资决策模型[J].中国管理科学, 2015, 23(7): 94-102. [12] 周艳丽, 吴洋, 葛翔宇. 一类高新技术企业专利权价值的实物期权评估方法--基于跳扩散过程和随机波动率的美式期权的建模与模拟[J].中国管理科学, 2016, 24(6): 19-28. [13] 甘柳, 杨招军.最优长期合同下的企业投融资决策[J]. 控制理论与应用, 2016, 33(11): 1483-1491. [14] 甘柳, 罗鹏飞, 杨招军.特质管理者决策下的企业投融资研究[J].系统科学与数学, 2016, 36(11): 1995-2006. [15] Alvarez L H R, Keppo J. The impact of delivery lags on irreversible investment under uncertainty[J]. European Journal of Operational Reasearch, 2002, 136(1): 173-180. [16] Sarkar S, Zhang Chuanqian. Implementation lag and the investment decision[J]. Economics Letters, 2013, 119(2):136-140. [17] Agliardi E, Koussis N. Optimal capital structure and the impact of time-to-build[J]. Finance Research Letters, 2013, 10:124-130. [18] Sarkar S, Zhang Chuanqian. Investment policy with time-to-build[J]. Journal of Banking and Finance, 2015, 55: 142-156. [19] 杨兆廷, 李吉栋. “担保换期权”与高新技术中小企业融资[J]. 管理世界, 2008, 10: 167-179. [20] 盛世杰, 周远游, 刘莉亚. 引入担保机构破解中小企业融资难:基于期权策略的机制设计[J]. 财经研究, 2016, (06): 63-73. [21] Yang Zhaojun, Zhang Hai. Optimal capital structure with an equity-for-guarantee swap[J]. Economics Letters, 2013, 118(2): 355-359. [22] Zhang Chunhong, Yang Zhaojun. Two new equity default swaps with idiosyncratic risk[J]. International Review of Economics and Finance, 2015,37: 254-273. [23] Wang Huamao, Yang Zhaojun, Zhang Hai. Entrepreneurial finance with equity-for-guarantee swap and idiosyncratic [J]. European Journal of Operational Research, 2015, 241(3): 863-871. [24] Xiang Hua, Yang Zhaojun. Investment timing and capital structure with loan guarantees[J]. Finance Research Letters, 2015, 13: 179-187. [25] Gan Liu, Luo Pengfei, Yang Zhaojun. Real option, debt maturity and equity default swaps under negotiation[J]. Finance Research Letters, 2016, 18: 278-284. [26] Goldstein R, Ju Nengjiu, Leland H. An EBIT-based model of dynamic capital structure[J]. Journal of Business, 2001, 74(4): 483-511. [27] Margsiri W, Mello A S, Ruckes M E. A dynamic analysis of growth via acquisition[J]. Review of Finance, 2008, 12(4): 635-671. [28] Leland H. Agency costs, risk management, and capital structure[J]. Journal of Finance. 1998, 53(4): 1213-1243.2.2 运营滞后
2.3 信用担保互换
3 模型构建与分析
3.1 担保成本的计算
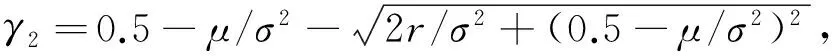
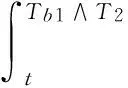
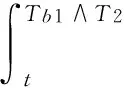

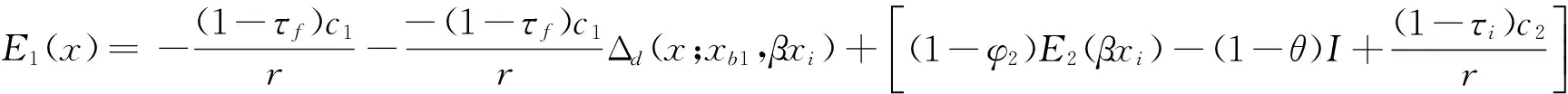
3.2 信用担保下的投资决策模型
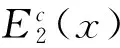

4 数值分析
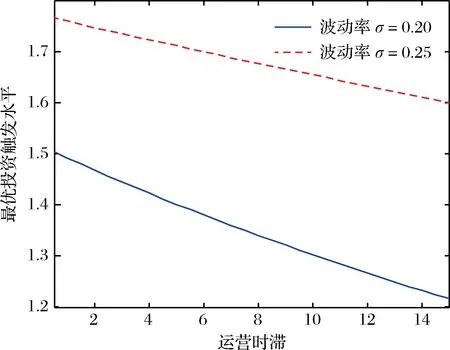
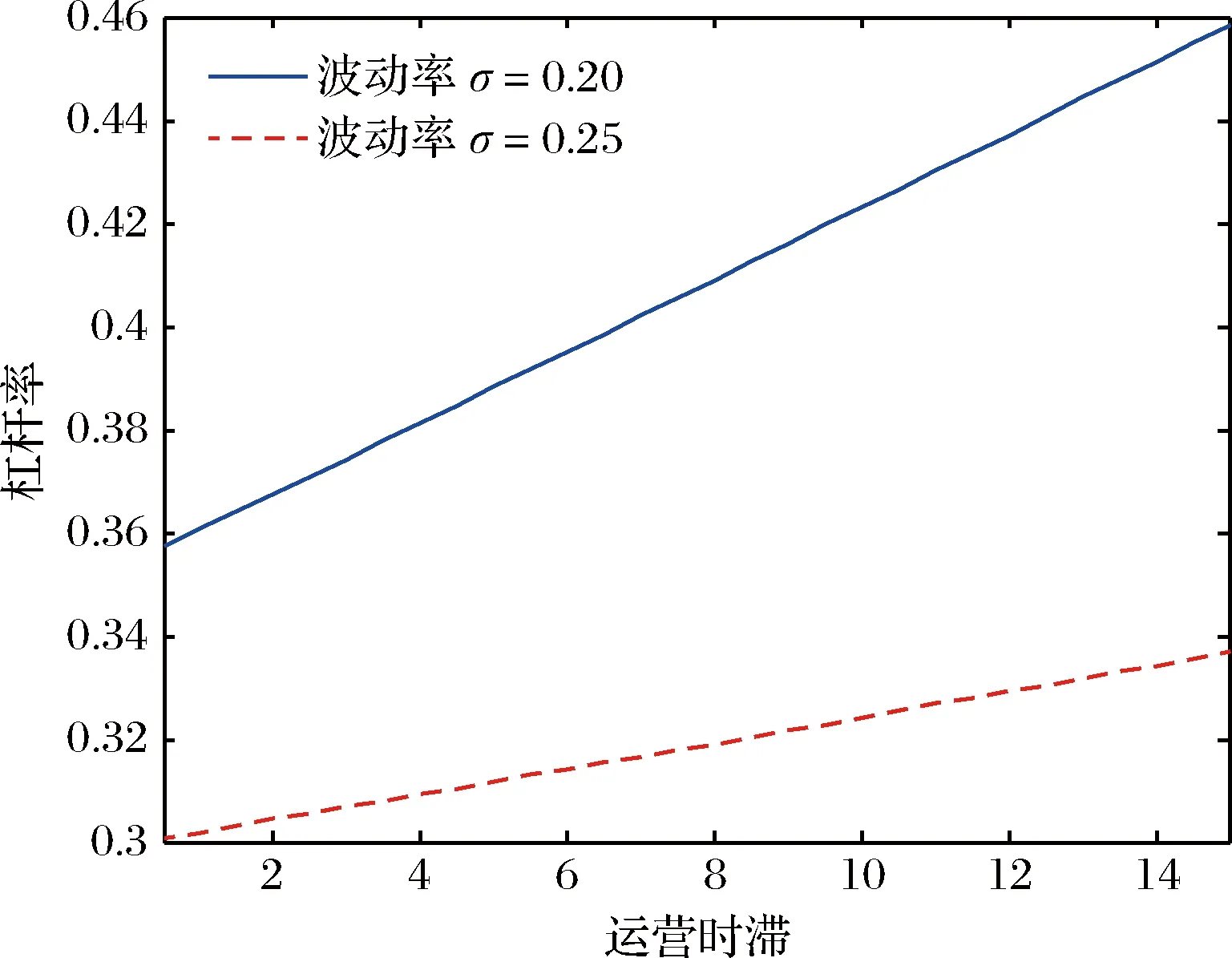
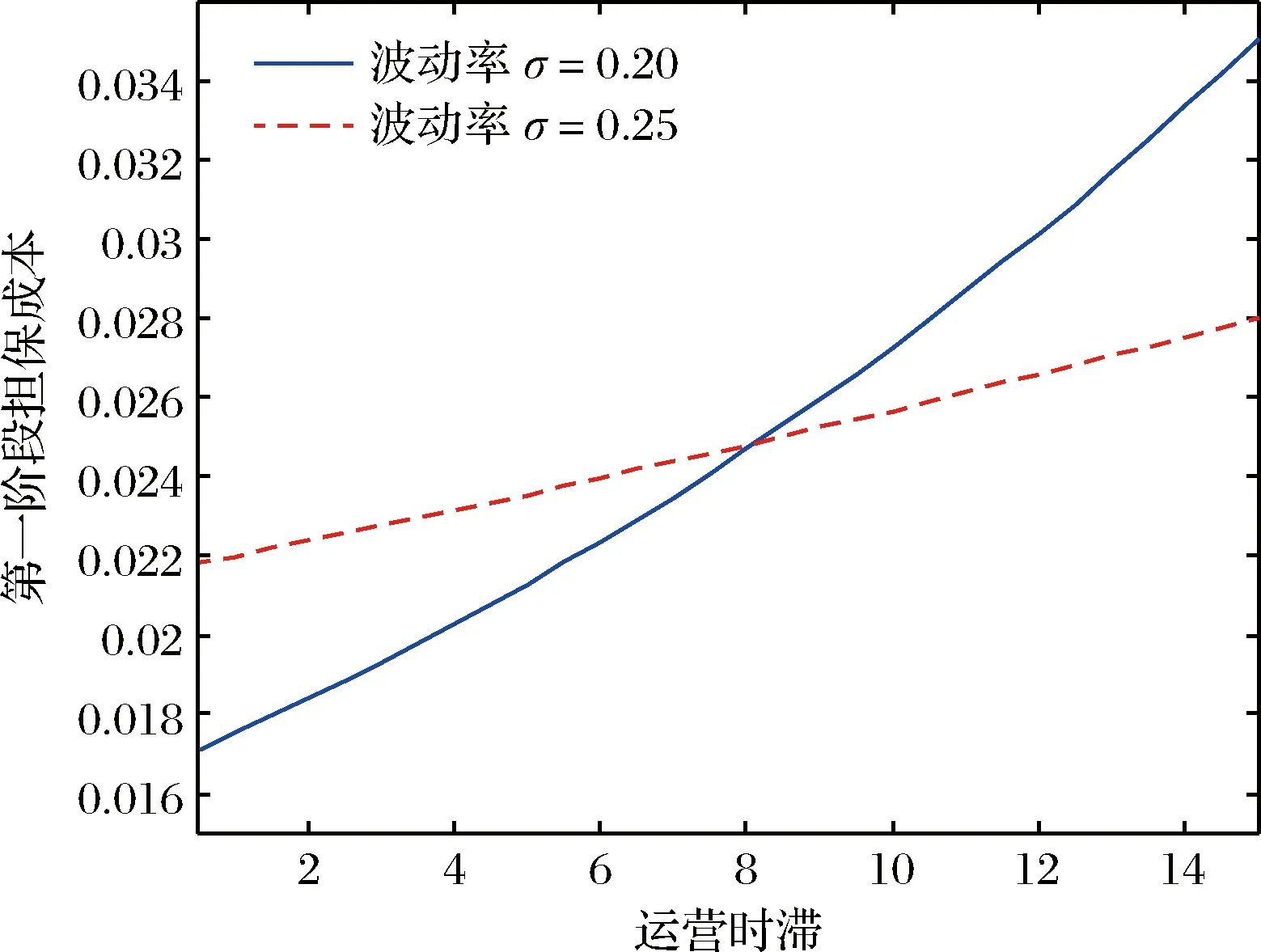
4.1 运营时滞的影响
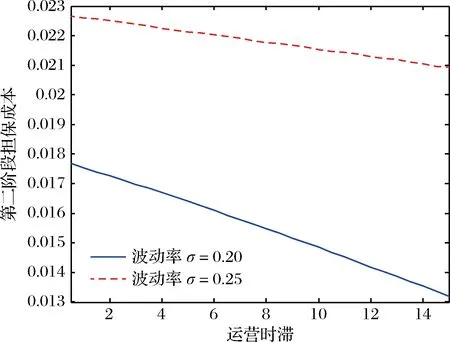
4.2 投资比重的影响
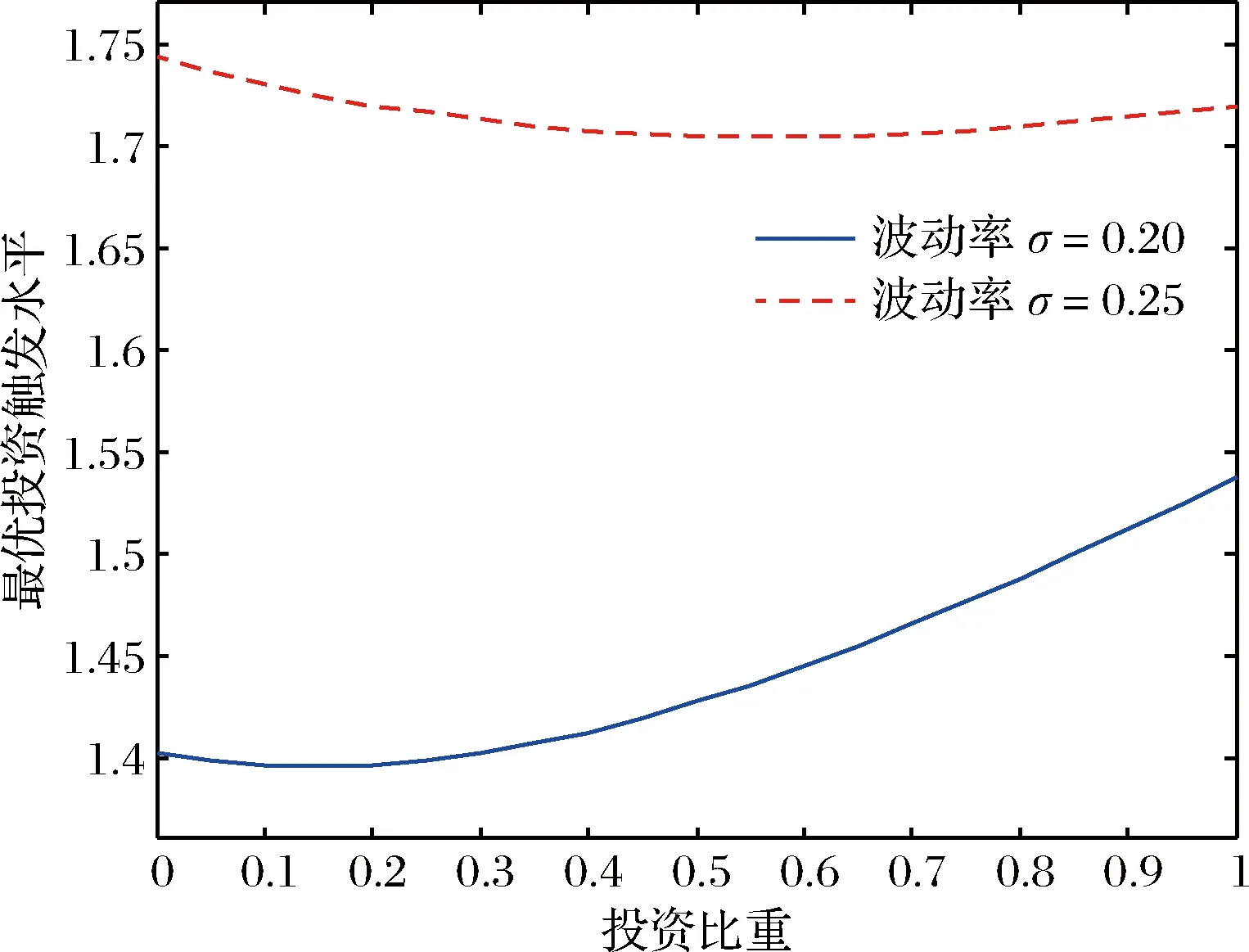
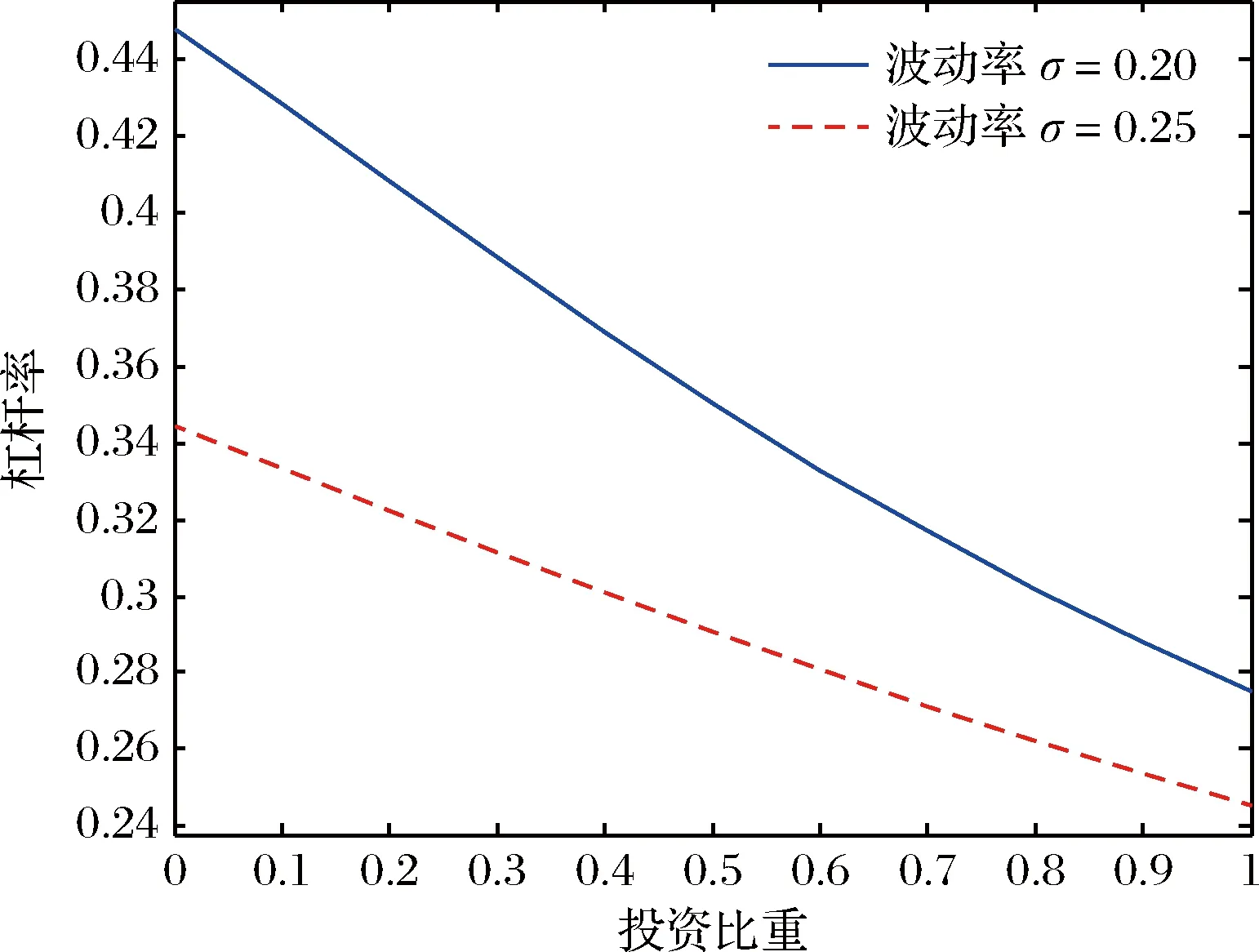
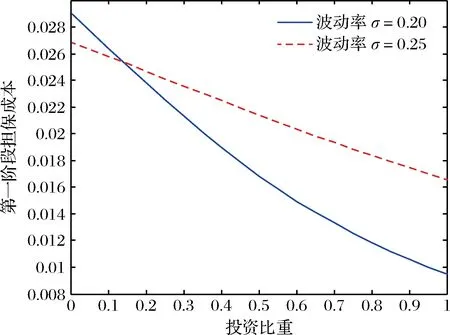
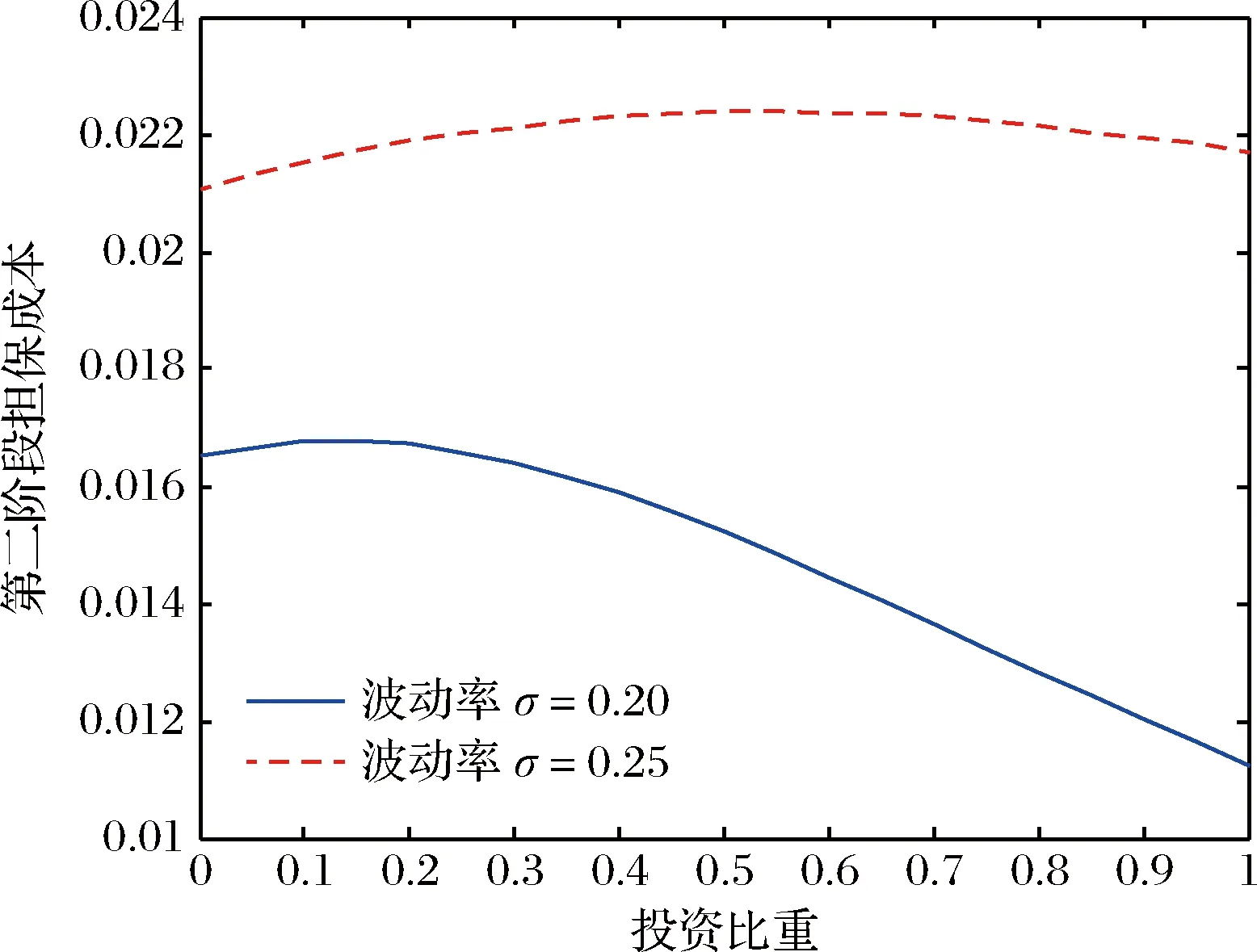
4.3 券息的影响
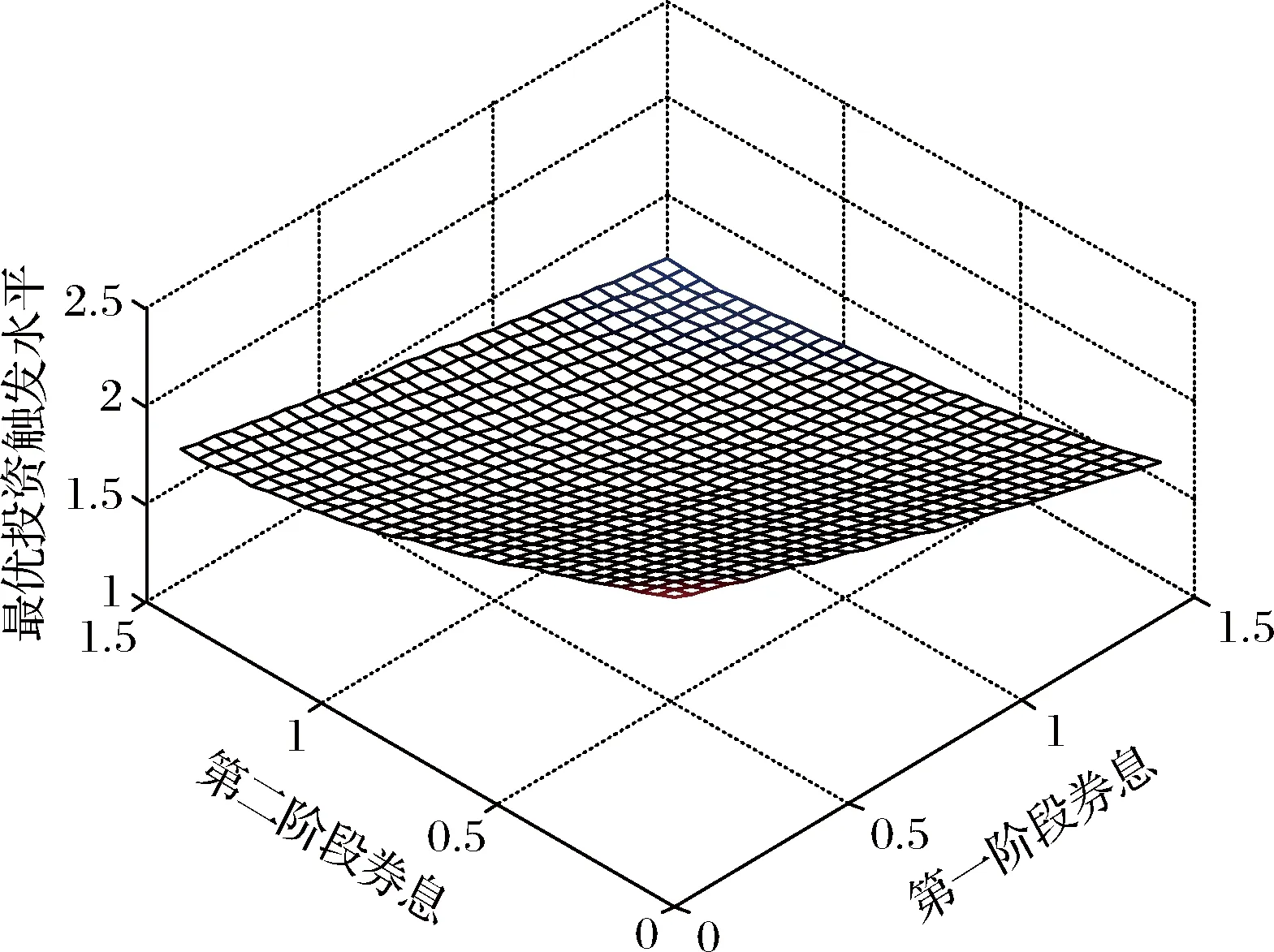



5 结语