求函数值域的方法探讨

云南省曲靖工商职业技术学校 陈 继

高中数学中，函数值域问题属于函数的综合性问题。虽然高中学生具备一定的逻辑思维能力，但是由于函数值域的题型和求法很多，如果学生没有掌握有效的求值域的解题方法，解题中就难以获得准确的答案。高中数学中，求函数值域是高考数学的重点和难点。本论文针对最值问题的解题方法展开研究。

一、高中函数题的解题中采用配方法求函数值域

在数学解题中采用配方法，就是把一个解析式利用恒等变形的方法，把其中的某些项配成一个或几个多项式正整数次幂的和的形式。通过配方解决数学问题的方法叫配方法。其中，用得最多的是配成完全平方式。配方法是数学中一种重要的恒等变形方法。配方法最主要的目的就是将一个一元二次方程或二次多项式化为一个完全平方式，以便简化计算，使变量减少，使问题简化。

比如，求函数值域的数学题：y=7- 4sinxcosx十4cos2x-4cos4x，求函数的最大值和最小值？

对于这道函数式的解题方法有两种：

第一种解题方法：

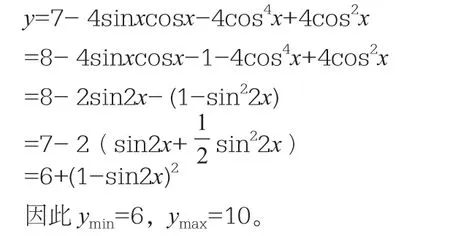
第二种解题方法：

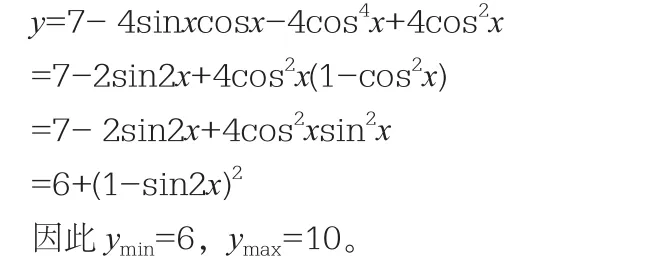
这道函数题的主要考查点是三角恒等变换，同时还对二次函数的相关知识和三角函数的相关知识进行考查。在高考数学题中会经常出现这种类型的数学题，属于常规的知识点。

二、采用换元法求函数值域

换元法就是以新变量代替函数式中的某些量，使函数转化为以新变量为自变量的函数形式，采用换元法求函数值域的方法，就是使抽象复杂的函数变得更为直观、简单、形象，变为普通常见的函数，从而简单快速地求出函数的值域，但是换元时一定要注意所换“元”的取值范围，它会影响函数的值域。比如，求函数的值域，采用换元法对原函数进行转化，转变为某个变量的二次函数，之后就可以将二次函数的值充分利用起来，对原函数的值域加以确定。

对于这道数学题，如果采用换元法，具体解题如下：

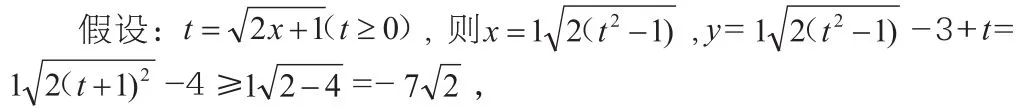
利用换元法求函数值域，一定要注意函数的结构形式，要明白哪种结构类型的函数可以用换元法，教师要引导学生仔细观察，认真审题。高中学生虽然具备一定的逻辑推理能力，但是习惯于解题中运用形象思维思考，用换元的方式解决数学问题，可以使得在数学解题中转换为学生已经掌握的数学知识。复杂的函数题通过换元后可以替换常见熟悉的函数，从而使学生的丰富想象力被激发起来，从已经掌握的知识出发理解数学题中所提出的问题，使学生在解答数学问题的时候，让复杂抽象而难以理解的数学题变得简单直观，容易理解，使复杂问题简单化，从而提高学生的解题能力。

三、采用判别式法求函数值域

在利用判别式法求函数值域时，也要弄清函数的结构，y是关于x的分式型二次函数，就是把函数y=f (x) 看作一个关于x二次方程，“x的二次方程 y=f (x)有实数解，判别式必须大于等于0，解一个关于y的一元二次不等式，从而求出y的取值范围。”判别式法是求函数值域的一个非常重要的方法，用于分式型二次函数的函数值域求解。

解：x2+x+1=(x+12)2+34＞0，所以函数的定义域是R。

去分母：y(x2+x+1)=x2-2x+1，得：(y-1)x2+(y+2)x+(y-1)=0。

当y≠1时，由Δ≥0得0≤y≤4；

当y=1时，将其代入方程中得x=0。

得出原函数的值域为[0，4]。

总之，函数值域的求法多种多样，根据函数结构类型掌握一定的函数求值域方法，有助于提高学生解题准确率，有助于培养学生的解题速度，有利于学生对函数知识的理解。