PXW型摆辗机摆头运动学分析及摆头运动轨迹研究

2018-03-28杨建东龚小涛

锻压装备与制造技术 2018年1期

耿佩，党杰，杨建东，龚小涛

（西安航空职业技术学院，陕西西安 710089）

摆动辗压简称摆辗，最早出现在20世纪30年代。它是一种局部加压的连续成形技术，具有省力、零件尺寸精度高、振动小、噪声低等诸多优点，正在逐步取代传统锻压加工中工具与坯料间断续（冲击式）、整体式接触施压方式[1]，因此可以用较小吨位的设备来成形较大的锻件，且可使成形件精度及对复杂形状零件的实用性、劳动条件等得到较大改善。

摆碾成形基本原理如图1所示。摆头中心线OZ与机器主轴中心线OM相交成角，此角称为摆角。当主轴旋转时，OZ绕OM旋转，于是上模便产生了摆动。与此同时，下模在油缸作用下上升，并对毛坯施压，这样上模母线就在毛坯上连续不断地滚动，最后达到整体成形地目的。相当于锥体沿母线在工件上滚动+滑动，接触面偏向一旁，即机床承受周期变形偏心载荷。摆头与坯料之间的接触面积是整体投影面积的1/n（n=5～10）倍，变形力仅为原来的1/n[2]。

图1 摆辗原理示意图

由波兰人设计制造的PXW型摆辗机是摆辗原理机型，也是最早投入生产的机型，并一直沿用至今。该机型主要特点是摆辗机摆头具有4种运动轨迹，可适应不同的加工场合[3]。后来研发出的摆辗机设备及其研究内容也主要是围绕PXW摆辗机来展开的。

1 摆头运动学分析

PXW型摆辗机摆头运动轨迹即为摆杆的运动轨迹，它是由两个独立的分支传动链来驱动两个偏心套（内、外偏心套）转动来实现的。由此可将摆头运动特征用内、外偏心套模型来表达，如图2所示。其中内偏心套圆心为 O1，外偏心套圆心为O，摆杆端面中心为O2。外偏心套绕其几何中心O旋转，内偏心套绕其几何中心O1旋转。外偏心套旋转时带豆内偏心套旋转（公转），而内偏心套旋转（自转）时，不影响外偏心套旋转。改变内外偏心套旋转速度和方向，可实现其同速同向、同速异向、异速同向和异速异向4种组合运动[4，5]。

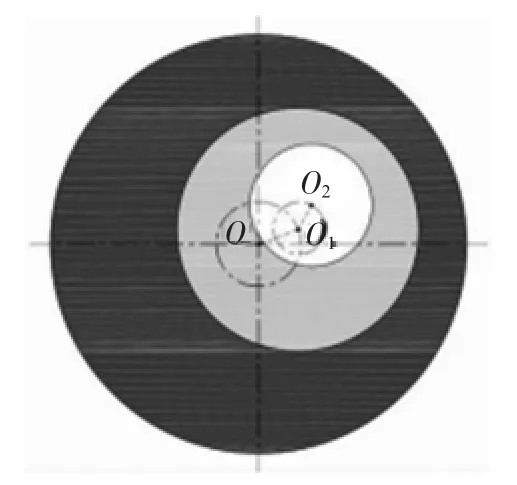
图2 内外偏心套模型

为进一步研究PXW型机内、外偏心套摆头的运动轨迹，简化图2所示双偏心套模型，换用矢量方法来表示，摆头运动轨迹的水平投影可用图3中矢量的终点位置来表示，它是由内、外偏心套两个旋转运动而合成的，其中内、外偏心套的偏心距为r，矢量的矢径与极坐标的角度分别为：

图3 内外偏心套矢量模型

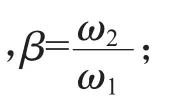
φ——摆头瞬时转角；

t——时间（min）。

2 摆头运动轨迹分析

基于上述摆头内、外偏心套运动模型，利用MATLAB软件对内、外偏心套不同运动方向和速度的组合情况进行模拟分析，发现：当内、外偏心套同向同速运动时，摆头的运动轨迹是以外偏心套几何中心O为中心，半径为2r的圆形轨迹，如图4a所示；当内、外偏心套同速反向旋转时，摆头轴端中心点运动轨迹是以外偏心套几何中心O为中心，长度为4r的一条直线，如图4b所示；当内、外偏心套异速同向旋转时，摆头轴端中心点运动轨迹是螺旋线，且螺旋线运动范围在半径2r的圆内，如图4c所示；当内、外偏心套异速异向旋转时，摆头轴端中心点运动轨迹是多叶玫瑰线，且多叶玫瑰线运动范围在半径为2r的圆内，如图4d所示。

图4 PXW型摆辗机摆头运动轨迹

3 摆头螺旋线运动轨迹形成过程

4 结论

基于PXW摆辗机内、外偏心套运动模型，通过运动学分析，建立摆头矢量坐标方程；运用MATLAB软件对内外偏心套不同运动组合进行数值模拟，验证了当内、外偏心套同向同速、同速反向、异速同向及异速异向旋转时，摆头运动轨迹分别为圆形、直线、螺旋线和多叶玫瑰线；模拟分析得出螺旋线运动轨迹的形成规律：在0-π时刻，摆头轴端中心点逐渐靠近轴心并同时做螺旋式上升；在π-2π时刻，摆头轴端中心点逐渐远离轴心并做螺旋式上升。