数控转塔冲床进给系统动力吸振器设计
2018-03-28王万杰涂芬芬王金荣
王万杰,周 祥,刘 冲,涂芬芬,王金荣
(江苏省金属板材智能装备重点实验室,江苏 扬州 225200)
数控转塔冲床进给系统在负载较大和X轴溜板位置工况较差的情况下,由于高加加速度导致振动偏大,振动的衰减时间也较长。为了优化进给系统的动态特性,一般可以从控制系统和传动结构优化的角度进行研究[1]。但这些优化手段设计周期较长,在短时间内难以实现,而且对当前已有的样机无法应用。因此在不修改原有进给系统结构的基础上,本文通过引入动力吸振器,尝试一种更加实用的进给系统优化方案。
动力吸振器(Dynamic Vibration Absorber,DVA)[2]作为一种简单易行的减振手段,在工程实践中得到广泛应用。其基本原理是:通过在主振系统上附加一个辅助结构,一般可以简化为由弹簧、阻尼、振子组成的一个单自由度系统。适当地选择动力吸振器的结构形式、优化匹配其参数,进而改善主振系统的振动传递特性,在振幅较大的频率范围内减小主振系统的受迫振动响应。
动力吸振器按是否有源,可以分为被动式和主动式两类[3]。传统的动力吸振器属于被动式,一经设定,各项参数就固定不变了,仅能够在固有频率附近的频段内有效。其优点是成本低、结构简单、易于安装。主动式吸振器可以根据主振系的振动状态,自动调节吸振器的结构参数或振动状态,实现宽频带吸振,从而拓宽吸振器的使用范围,提高减振效果[4]。
1 横梁频率响应分析
根据对数控转塔冲床横梁负载工况的分析,X轴溜板夹持的板材质量变大时,进给所需的总时间变长,也即等待衰减的时间变长,这是因为横梁在启停时受到的惯性力也随之增加。为了更加准确地了解横梁受到激励时Y方向的响应,还需要对其进行频率响应分析[5],找出影响数控转塔冲床横梁动态性能较大的模态振型和固有频率,并对横梁Y方向动刚度做定量分析。综合动静态分析和动力学分析结果可知当X轴溜板位于远离电机端时,横梁的动态特性最差,故选定该位置进行分析。
本节采用HyperWorks RADIOSS模块[6],基于模态叠加法对数控转塔冲床横梁进行频率响应分析。由于板材质量最大为100kg,加速度最大为1g,产生的最大惯性力为1000N。故而在夹持板材的中间夹头位置处Y方向加载1000N的激励力,如图1所示。我们主要关心横梁低阶模态,频率范围设置为5Hz~85Hz,间隔为 0.5Hz。
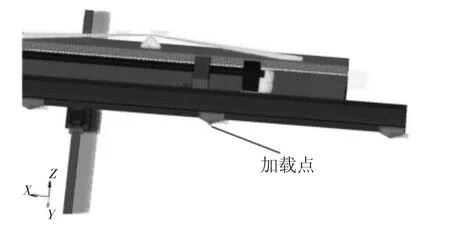
图1 频率响应分析激励点示意图
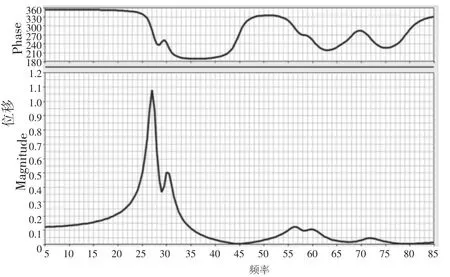
图2 中间夹头位置Y方向频率响应结果
如图2所示,中间夹头位置Y方向的响应在激励频率为27Hz处出现一个较大的峰值,振幅为1.08mm,对应该位置工况下横梁在水平面内转动的振型频率。在30.5Hz处出现的较小峰值是横梁端部振动模态的体现。
针对横梁在水平面内转动的振型,本文设计一款动力吸振器,以抑制频率响应幅值较大处的振动。
2 动力吸振器设计
2.1 动力吸振器设计思路
动力吸振器设计的基础是定点理论[7]。定点指的是频率响应函数上与阻尼无关的特定的点,对于含有阻尼α的振动系统,α=0和α=∞的传递函数的交点不依赖α。通常定点有两个,不同α的传递函数均经过这两个交点。把这两个定点的高度调整为等高称为最优同调,而使定点处于曲线最大值位置的α称为最优阻尼。
主振动系统一般为具有许多模态的多自由度系统。其中,我们把对主振动系统,即冲床横梁性能影响最大,也是我们最关心的一个模态提取出来,将主振动系统等效简化为一个没有阻尼的、质量为M、刚性为K的单自由度振动系统,作为我们的研究对象。在这个单自由度系统之上,附加上质量为m、刚度为k、阻尼系数为c的动力吸振器,构成如图3所示的力学模型。主振动系统一般存在阻尼,但正是因为阻尼较小才产生振动问题[8],且冲床横梁主要由两根空心方管焊接而成,因此这里忽略主振动系统的阻尼来进行动力吸振器的设计。
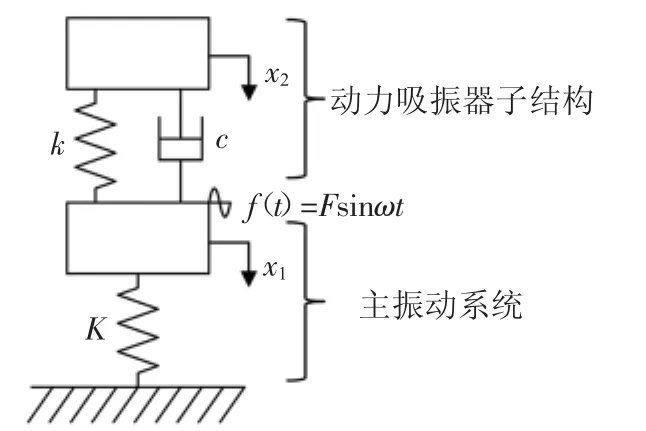
图3 主振动系统上附加了动力吸振器的力学模型
横梁上的激励主要为直接作用在结构上的激振力,在此,假定这些激励具有正弦波的特征,在图3中表示为f(t)=Fsinωt。主振动系统与动力吸振器的位移分别用x1和x2表示,则系统的运动方程式为
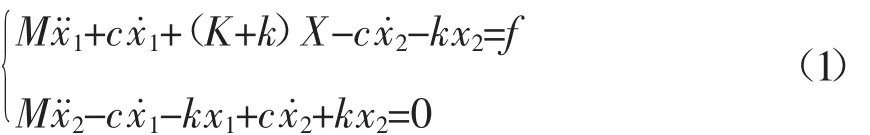
把激励力写成f=Fejwt,主振动系统与动力吸振器的位移可以表示为为x1和 x2的复数振幅。求解这个方程组并用的形式来表示:
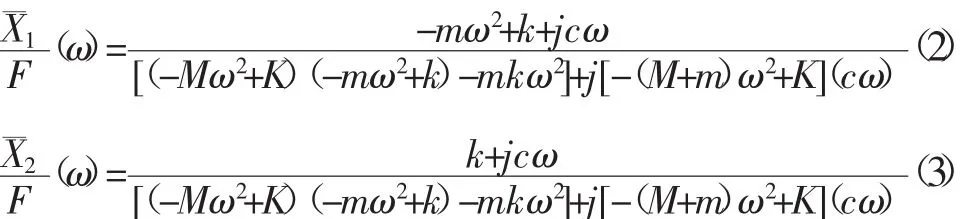
分子分母同除以(Mm)2,并引入以下各项:
Ωn=:主振动系统的固有角频率,rad/s;
ωn=动力吸振器的固有角频率,rad/s;
Xxt=F/K:主振动系统的静变形,m;
μ=m/M:质量比;
ξ=c(/2mΩn):阻尼比;
λ=ω/Ωn:强迫振动频率比;
γ=ωn/Ωn:固有角频率比;
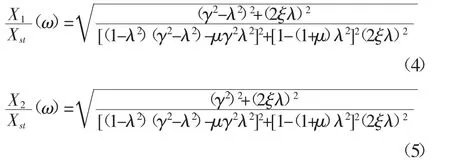
其中X1/Xst为主振动系统位移的振幅比,使这个值最小就是动力吸振器的设计目标。为达到这个设计目标,需要满足最优同调条件和最优阻尼条件。这两个条件为:
则可以推导出质量比μ为参数的动力吸振器3个元素的设计公式为:
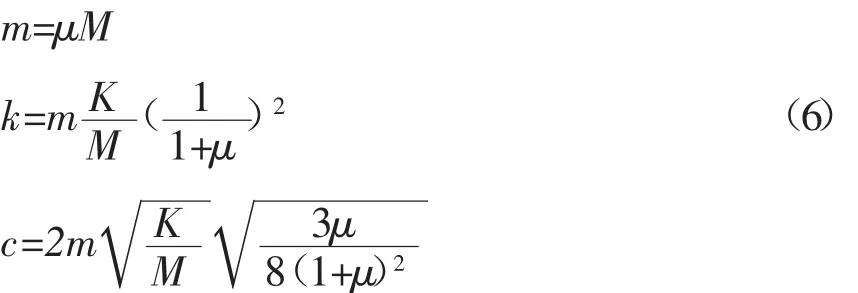
在满足最优设计条件时的最大振幅比为:

其中Xst为主振系统在与简谐力相等的静力作用下的变形。
2.2 模态等价质量计算
上一节中的主振动系统质量M和刚度K为需要控制的模态对应的等价质量和刚度,接下来计算这两个参数。等价质量识别有固有模态法和质量感应法。
固有模态法又称特征向量法,是利用总能量相等的原则,把离散化之后的主系统所有位置的振动总能量等价到动力吸振器的安装点上。这种方法的识别精度与离散的点数有关,需要先做模态分析,离散系统以及计算振型向量。
而质量感应法的原理是在主系统上附加一个质量,改变其固有频率,通过附加质量前后的固有频率关系来推算出主系统的等效质量。该方法把对象结构的某一阶模态的振动,当作一个单自由度系统的振动来看待。第i阶模态在j点的等价质量可由以下公式求得:

该方法直观易懂、原理简单,操作与固有模态法相比更方便[9]。但是对于冲床横梁来说,本身结构较为复杂,而且考虑了结合面等因素,振型比较复杂。故该方法的使用很大程度上依赖经验,因为附加质量太小的话,固有频率的变化不明显;反过来附加质量太大,模态间的耦合效应会引起误差,甚至会使该阶振型发生变化,以致不能正确地识别模态质量。故本文使用固有模态法来计算。
对于n自由度系统,第i阶模态的固有向量

与这个固有向量对应的振动模态(ω=ωi),上的各点速度可以写成

则,系统全体的动能Ttotal由下式给出
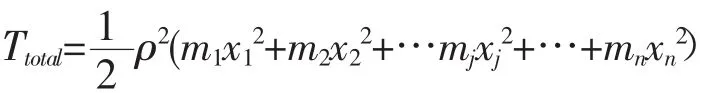
j点的动能
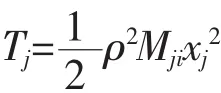
Mij定义为第i阶模态在j点的等价质量,Kij为其等效刚度。
令 Tj=Ttotal,可得
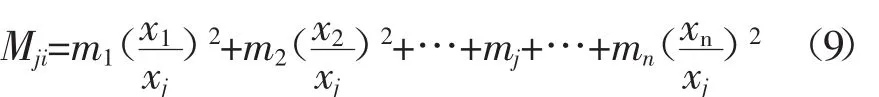
从式(9)可以看出:①若点j处于模态的最大变形位置,得到的等价质量为最小。②若点j处于模态的节点(变形为0的节点),等价质量为无限大。
本文动力吸振器针对横梁溜板在远离电机端位置工况下的约束模态第三阶,即i=3,根据第二章中的计算结果固有频率fi=27.14Hz,那么角频率Ωi=2πfi=170.53rad/s。因为模态变形的比值是一定的,因此可以按照模态变形的比值确定其模态固有向量大小的比值,针对横梁在水平面内转动的振型,横梁上任意点的固有向量大小与其到约束位置的距离成正比。
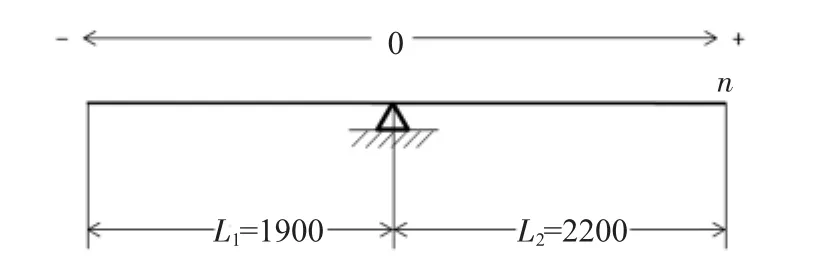
图4 横梁质量分布示意图
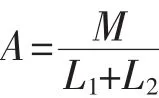
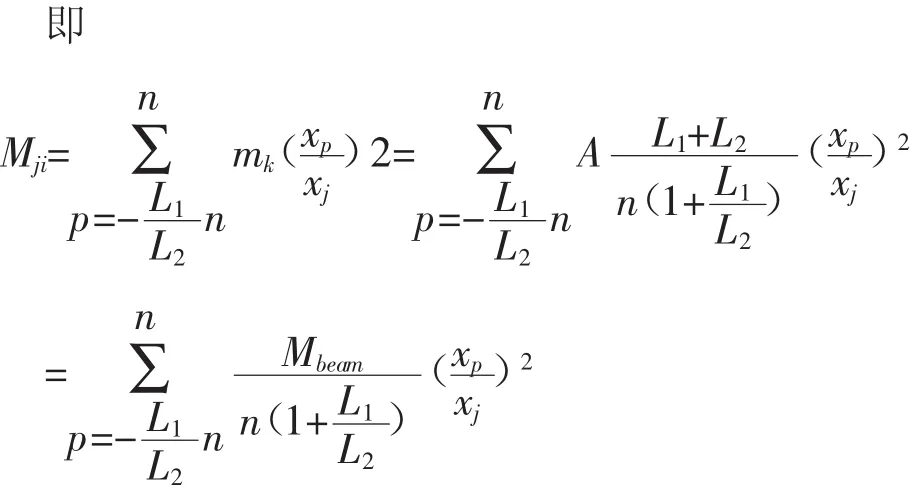
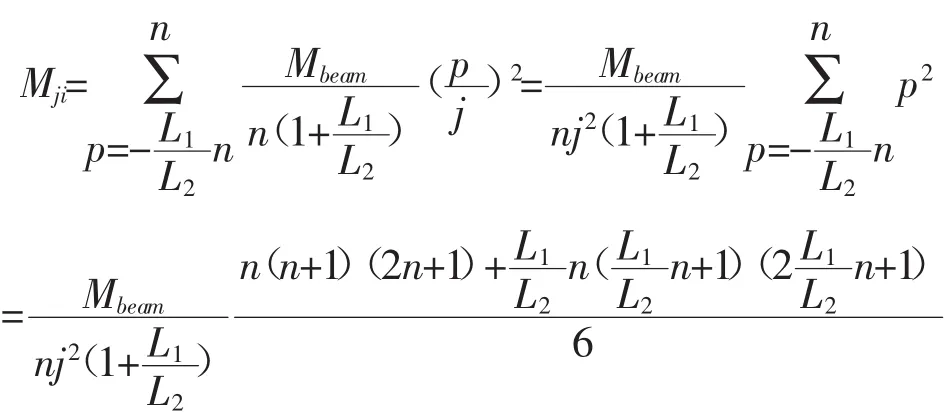
整理得
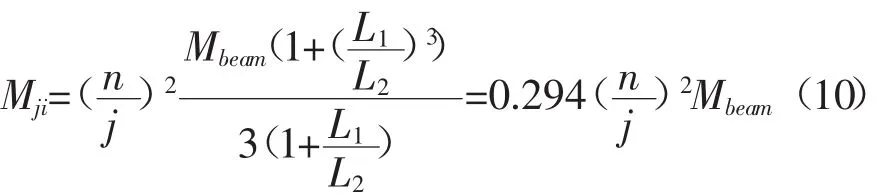
2.3 动力吸振器参数计算
根据以下几个准则来确定动力吸振器的安装位置:①针对该阶模态制振效果最好。②与其他模态不干涉。③从实用的角度易于安装和拆卸。
根据在满足最优设计条件时的最大振幅比公式(7)可知,动力吸振器的制振效果取决于质量比,质量比越大制振效果越好。在动力吸振器质量不变的情况下,等价质量最小的位置,质量比为最大。由(10)式可见,模态质量与该点到约束位置距离的平方成反比,则越接近横梁端部等价质量越小,故应将动力吸振器安装在尽量靠近横梁端部的地方。由于横梁两侧端部都有护罩阻挡,而远离电机端部距离中间约束位置更大,所以本文将动力吸振器设计在横梁远离电机端与中间位置相距J=2000mm处。
本文中取 μ=0.1,则

此时主振系统的最大振幅比为
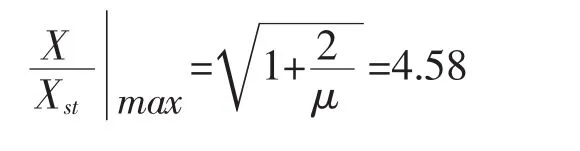
3 动力吸振器频率响应分析
如图5所示,为有限元建模示意图:其中CONM2为质点单元,模拟动力吸振器质量,而CELAS1为弹簧阻尼单元,模拟动力吸振器的刚度和阻尼,将质点与横梁方管相连。位置为横梁远电机端横置方管上方,距中间位置2000mm处。各参数按照上一节的计算结果设置。

图5 动力吸振器有限元建模示意图
安装有动力吸振器模型的横梁频率响应曲线如图6所示。在该位置安装动力吸振器后,27Hz处的峰值消失,24Hz处出现一个较为平缓幅值较小的峰。原先30.5Hz处的峰值变为最大振幅,大小为0.49mm。即X轴溜板中间夹钳位置在各频率激励下最大振幅为原来的45.4%,减振效果明显。
4 总结
本文通过对数控转塔冲床进给系统进行频率响应分析,找出受不同频率激励下振幅最大的频率点。基于动力吸振器原理,针对该频率点处的振型计算出动力吸振器的各项参数,建立了带有动力吸振器的进给系统模型。通过对改进的进给系统模型的频率响应分析,证明该动力吸振器对设计频率附近良好的减振效果。
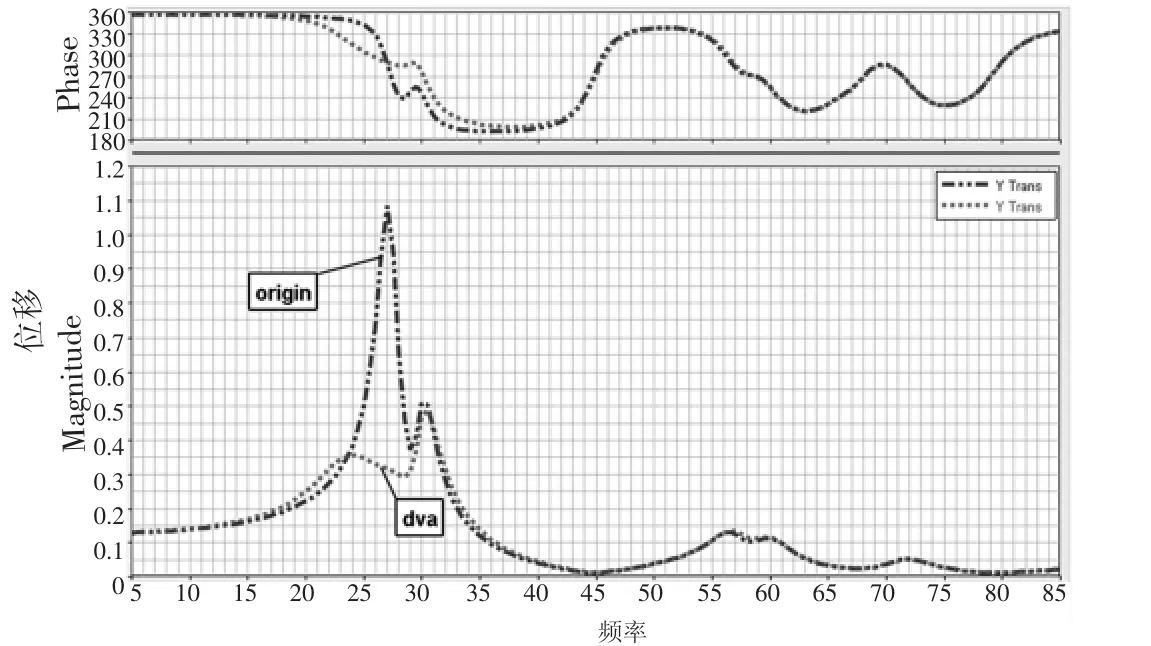
图6 动力吸振器频率响应
[1] 于卫红.数控转塔冲床横梁结构的分析与优化设计[J].南京师范大学学报,2010,10(2):21-26.
[2] 孙庆鸿.振动与噪声的阻尼控制[M].北京:机械工业出版社,1993.
[3] 张 鲲.带有动力吸振器浮筏隔振系统的减振特性研究[D].合肥:中国科学技术大学,2008.
[4] 盛美萍,王敏庆,孙进才.噪声与振动控制技术基础[M].北京:科学出版社,2007.
[5 渠鸿飞,褚夫强,尹绪超,等.动力吸振器在电动机振动控制中的应用[J].噪声与振动控制,2014,34(5):223-227.
[6] 梅 宇.基于RADIOSS模态分析的电路板抗振设计的研究[J].机械与电子,2015,(1):18-21.
[7] 背户一登,任明章.动力吸振器及其应用[M].北京:机械工业出版社,2013.
[8] 郝帅瀛.轿车悬架动力吸振器设计与匹配[D].长春:吉林大学,2011.
[9]何 山.动力吸振器的设计方法研究及其在汽车减振降噪中的应用[D].广州:华南理工大学,2014.
