连续射击过程中加速运动弹丸激励下身管横向振动特性研究

周奇郑， 赵 洋， 王德石

(海军工程大学 兵器工程系，武汉 430033)

火炮振动对射击精度有重要影响，炮口振动一直是研究者关心的主要问题。炮口运动状态影响了弹丸出口的初始状态，决定了弹丸的外弹道特性。连续射击过程中，弹丸激励身管振动的累积导致了炮口振动幅度的增加，使弹着点的散布增大，致使火炮射击精度降低。因此，研究连续射击过程中，弹丸加速运动对身管振动特性的影响规律，对确定火炮的射速、提高射击精度具有重要的理论与实际意义。

火炮的振动在实际射击过程中是不可避免的，其对射击精度的影响最终是由炮口振动反映出来的。发射过程中身管的受力情况十分复杂，通常仅考虑膛内压力、身管和弹丸的重力，但实际上还应包含身管及弹丸的各类惯性力、布尔登载荷、膛内旋转摩擦力矩、身管配套装置的作用力等[1]。由于身管尺寸大，刚度小，加之承受高膛压及高速运动弹丸的冲击作用，其振动有其特殊性，故许多学者把火炮振动研究的重点集中在身管的振动上。理论上，身管的振动可归结为悬臂梁的振动，弹丸可简化为移动质量，即身管振动可转化为移动质量作用下悬臂梁的振动。张永昌等[2]在等截面Bernoulli-Euler梁理论的基础上，考虑射击过程中身管的剪切变形、弹丸惯性力矩等作用，建立了火炮身管横向振动的二阶偏微分方程。利用此方程可确定内膛弯曲度、身管热变形、弹丸偏心率、内弹道诸元和身管结构等对射弹散布的影响。叶开沅等[3]针对列车过桥的整个过程，采用小参数法给出了任意单个移动激励作用下铁路桥梁动力学方程的一般解。文献[4]将叶开沅等的分析方法应用于火炮振动领域，研究了弹丸膛内运动引起的火炮身管横向振动问题，给出了单发及连发射击时炮管横向振动的一般解，进行了定性分析，未给出定量计算结果。姜沐等[5]将弹丸膛内运动近似处理为匀加速运动，建立了加速弹丸作用下火炮身管振动方程，并给出了级数形式的解析解和定量计算结果。史跃东等[6]在考虑弹丸匀速运动惯性效应的基础上，研究了身管振动特性，给出了解析解，分析了不同运动参数对炮口振动的影响规律，给出了定量比较结果。朱文芳等[7]利用一维两相流内弹道模型及一维圆管热传导模型，描述了某榴弹炮多发连续射击过程中身管的传热过程。目前，国外关于火炮身管振动方面的研究鲜见报道，Michaltaos等[8]研究了移动质量对简支梁的影响，对研究的背景未作深入的阐述。

由于在弹丸加速运动激励的振动系统中，弹丸的瞬时冲击作用将使得身管的固有特性随运动位移或运动时间变化，使得求解弹丸连续冲击作用下身管的振动更为复杂。因此，到目前为止，在火炮振动研究领域内，关于这方面的研究工作还较少，理论分析与定量计算也不多。在以往研究的基础上，本文将建立弹丸膛内加速运动下火炮身管横向振动方程，研究火炮连续射击过程中身管振动特性，为确定火炮的射速、提高射击精度提供技术基础。

1 加速弹丸作用下身管横向振动方程

将身管简化为Bernoulli-Euler均匀等截面悬臂梁，假定弹丸在膛内加速运动，考虑图1所示的身管横向振动模型。图1中：mp为弹丸质量；θ为射角；l为身管长度；v、a为弹丸膛内运动速度和加速度；y(x,t)为身管在坐标(x,0)处的挠度；F(t)为不计惯性效应时弹丸膛内运动作用于身管上的等效合外力。

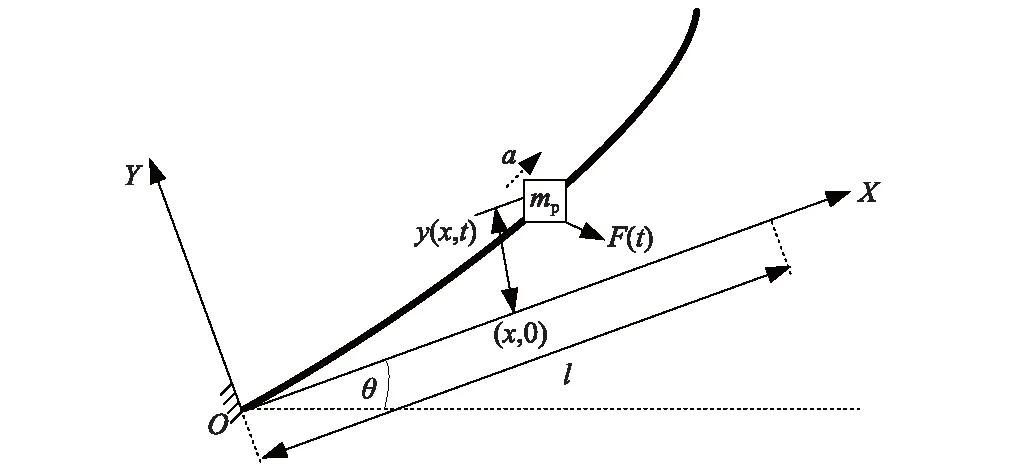
图1 弹丸加速运动作用下身管横向振动模型Fig.1 Transverse vibration model of barrel subjected to accelerating projectile

设身管的抗弯刚度为EI， 密度为ρ， 横截面积为A。 取纵坐标为OY，横坐标为OX。在计及阻尼和弹丸惯性效应时，加速弹丸作用下身管的横向振动方程为(OY方向为正向)

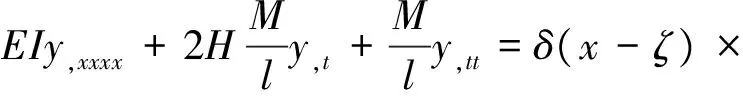
(1)

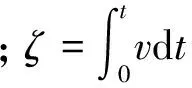
y,x|x=0=0,y|x=0=0
y,xx|x=l=0,y,xxx|x=l=0

(2)

y,t|t=0=v0,y|t=0=y0

(3)

由于弹丸与身管的质量比ε=mp/M≪1，取其为小参数，式(1)可写为

y,tt+2Hy,t+Gy,xxxx=lδ(x-ζ)(-f(t)-
ε(y,tt+ay,xt+2vy,xt+v2y,xx))

(4)

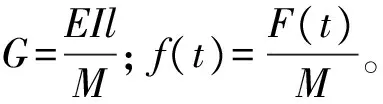
2 第一发弹丸作用下身管横向振动方程的解

对于式(4)，在边界条件式(2)和初始条件式(3)下，可采用小参数法进行求解。将式(4)的解y展开为小参数ε的幂级数形式，即

y(x,t)=y0(x,t)+εy1(x,t)+
ε2y2(x,t)+…

(5)

将式(5)代入式(2)～式(4)中，同时将ε因次相同的项合并在一起，可得一系列关于y0，y1，y2，…及相应边界条件、初始条件的微分方程。

对于y0，有如下方程、边界条件和初始条件

y0,tt+2Hy0,t+Gy0,xxxx=-f(t)lδ(x-ζ)

(6)

y0,x|x=0=0,y0|x=0=0
y0,xx|x=l=0,y0,xxx|x=l=0

(7)

y0,t|t=0=0,y0|t=0=0

(8)

令y0的解为

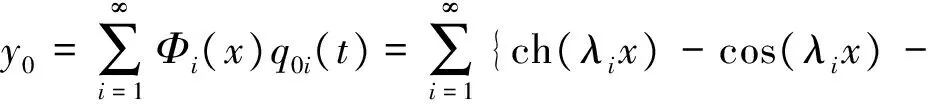
(9)

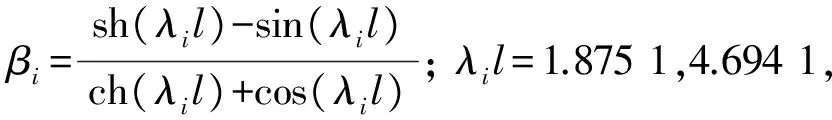
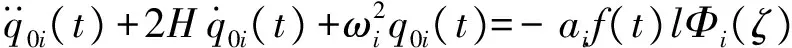
(10)

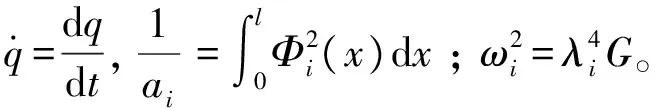
(11)

采用Duhamel积分求解式(10)，可得

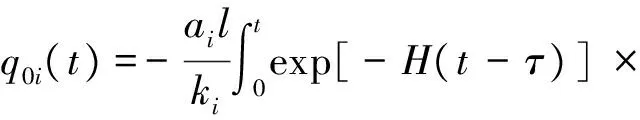
(12)

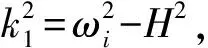
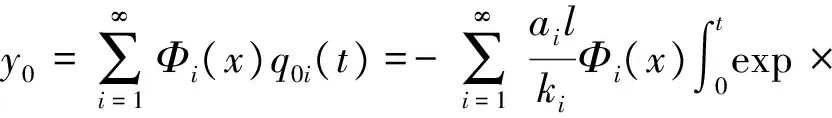
(13)

对于y1，有如下方程，边界条件和初始条件

y1,tt+2Hy1,t+Gy1,xxxx=-lδ(x-ζ)(y0,tt+
ay0,xt+2vy0,xt+v2y0,xx)

(14)

y1,x|x=0=0,y1|x=0=0
y1,xx|x=1=0,y1,xxx|x=1=0

(15)

y1,t|t=0=0,y1|t=0=0

(16)

令y1的解为

(17)

将式(13)、式(17)代入式(14)和式(16)中，可得如下方程及初始条件

(18)

(19)

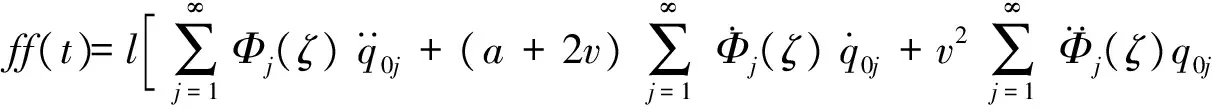
对于y2，y3，…，可按同样思路求解，将其全部代入式(5)，即可得身管横向振动位移y级数形式的解析表达式。

3 连续射击过程中身管横向振动方程的解

由于火炮机械条件的限制，只有前一发弹丸射出身管之后才能装填下一发弹丸，因此，连续射击过程中，对于第j发弹丸激励下身管的振动，其方程同式(1)，只是方程的初始条件发生了变化，即

yj,t|t=0=yj-1,t(jtg),yj|t=0=yj-1(jtg)

(20)

式中：tg为射击间隔。同样可以采用小参数法进行求解，对于第j发弹丸激励的振动yj,0有

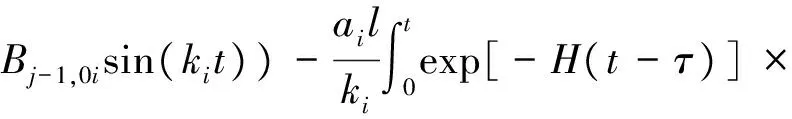
(21)

采用类似方式，可以得到对应于第j发弹丸的其余方程，从而可以得到连续射击过程中，身管的振动响应。

4 振动算例

考虑弹丸膛内的变加速运动，将弹丸对身管的作用力分两种情形讨论，一种为弹丸无质偏的情形，一种为弹丸有质偏的情形。

4.1 弹丸无质偏

当不考虑弹丸质偏时，式(1)中等效合外力F(t)即为弹丸质量对身管的作用力，有

(22)

由于f(t)为ε的一次式，易知采用小参数法求解振动方程时，y中的y0分量恒为0，即只须计算ε的非0次项，设

y(x,t)=εy1(x,t)+ε2y2(x,t)+…

(23)

将式(22)、式(23)代入式(4)中，整理可得对应于yq和uq(q=1,2,…)的振动方程，以y1和u1为例有

y1,tt+2Hy1,t+Gy1,xxxx= -lgcosθδ(x-ξ)

(24)

式(24)边界条件、初始条件和求解方法与前面介绍的完全一致，在此不再赘述。求得y1，采用类似方法可迭代求出y中其余各项，叠加得到第一发弹丸激励下身管的振动响应，然后按第2部分内容求解第j发弹丸的冲击振动响应。

研究弹丸无质偏情形下，身管阻尼系数、射击间隔对身管振动特性的影响。参数选取：弹丸质量mp=13.5 kg，身管长度l=5.5 m，射角θ=45°，弹性模量E=210 GPa，重力加速度g=9.8 m/s2。对于该口径弹丸，由试验测得了膛内运动过程中的加速度，经样条插值得到如图2所示弹丸加速度随无量纲时间的变化曲线[9]，该曲线与膛内火药气体压力具有相同的变化规律。由于获得了弹丸加速度的数值解，因此，在采用Duhamel积分求解qi(t)时需采用卷积定理进行求解。

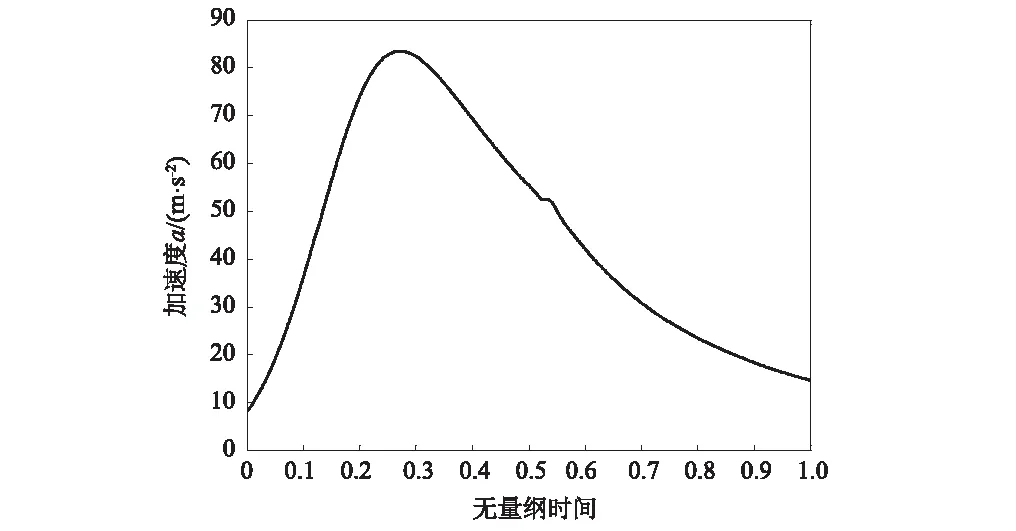
图2 弹丸加速度随无量纲时间的变化曲线Fig.2 The projectile acceleration versus dimensionless time

图3为弹丸无质偏时炮口振动位移随时间的变化曲线，由于仅考虑了弹丸重力的影响，弹丸膛内运动时，炮口振动位移为负值，最大位移为-5.86×10-6m；弹丸飞离炮口后，炮口做衰减振动，其衰减速度随系统阻尼系数H的增大而加快。图4为发射间隔对炮口振动位移的影响，由图4知，发射间隔为16 ms时，第二发弹丸激起的炮口振动的最大振动幅值为5.60×10-5m，第三发弹丸激起的炮口振动的最大振动幅值为2.35×10-4m，炮口振动幅值随连续射击的弹丸数急剧增大；发射间隔为25 ms时，第二发弹丸激起的炮口振动的最大振动幅值为2.88×10-5m，第三发弹丸激起的炮口振动的最大振动幅值为4.78×10-5m，炮口振动幅值随连续射击的弹丸数增大缓慢；发射间隔为50 ms时，弹丸激起的炮口振动的最大振动幅值为-5.86×10-6m，即与单发弹丸激励的幅值相同，但弹丸在膛内运动时，身管衰减振动明显；发射间隔为80 ms时，弹丸激起的炮口振动的最大振动幅值为-5.86×10-6m，此时前一发弹丸对后一发弹丸的影响可以忽略。即弹丸无质偏情形下，火炮的发射间隔最小应为80 ms。

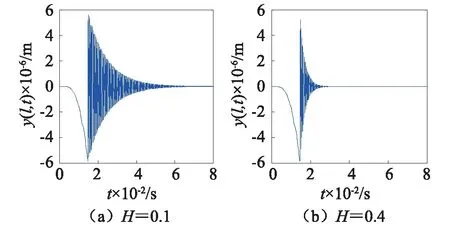
图3 弹丸无质偏时炮口振动位移Fig.3 Vibration displacement of muzzle without mass-unbalance projectile

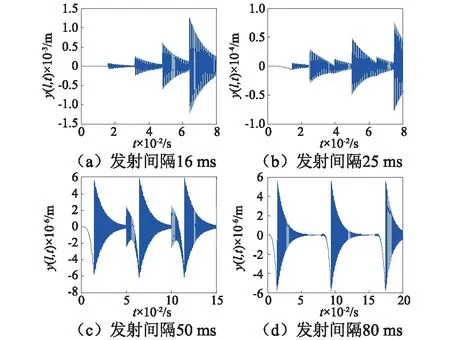
图4 弹丸无质偏时发射间隔对炮口振动的影响Fig.4 Influence of launching intervals to muzzle vibration without mass-unbalance projectile

4.2 弹丸有质偏

膛内运动时，由于受到膛线的作用，弹丸沿身管轴线方向除作高速平移运动处，还将沿膛线作高速旋转运动。如果弹丸存在质偏，膛内的高速旋转运动将导致极大的离心力，从而影响弹丸与身管之间的作用力。即F(t)中应含有弹丸自重和离心力对身管的作用：

F(t)=mpgcosθ+mpRsϖ2sin (ϖt)

(25)

式中：Rs为弹丸质量偏心距； ϖ为弹丸膛内运动转速。对于等齐膛线的身管，由弹道学相关理论可知

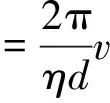
(26)

式中：η为缠度；d为身管内径。将式(25)、式(26)代入F(t)的表达式，有

(27)

求得f(t)后，与弹丸无质偏时采用相同的处理方法，即可完成问题的求解。

参数选取：η=27，Rs=10-4d，其余参数同上。图5为弹丸有质偏时炮口振动位移随时间的变化曲线，由于考虑了弹丸重力和质偏的影响，弹丸膛内运动时，炮口振动位移的最大幅值为7.15×10-6m；由于弹丸旋转产生的离心力的作用，单次射击周期内炮口的振荡次数增多了；弹丸飞离炮口后，炮口做衰减振动，与弹丸无质偏时的情形一致。图6为发射间隔对炮口振动响应的影响，由图知，发射间隔为16 ms时，第二发弹丸激起的炮口振动的最大振动幅值为6.95×10-5m，第三发弹丸激起的炮口振动的最大振动幅值为2.63×10-4m，炮口振动幅值增加较快，将使弹着点的散布增大，射击精度降低；发射间隔为25 ms时，第二发弹丸激起的炮口振动的最大振动幅值为2.81×10-5m，第三发弹丸激起的炮口振动的最大振动幅值为3.23×10-5m，炮口振动幅值增加较慢；发射间隔为50 ms时，弹丸激起的炮口振动的最大振动幅值为7.15×10-6m，即，炮口振动幅值保持不变，但弹丸在膛内运动时，身管衰减振动明显；发射间隔为100 ms时，弹丸激起的炮口振动的最大振动幅值为7.15×10-6m，此时前一发弹丸对后一发弹丸的影响可以忽略，即弹丸有质偏情形下，火炮的发射间隔最小应为100 ms。

上述分析表明，身管的阻尼系数H主要影响弹丸出口后身管的衰减振动，阻尼系数越大，身管振动衰减越快，前一发弹丸对后一发弹丸的影响越小；弹丸发射间隔的主要影响体现在后一发弹丸引起的振动上，发射间隔越短，炮口处振动的增幅增加越快；当发射间隔达到一定值后，前后两次射击将不会相互影响。因此，对于中大口径火炮，适当增大发射间隔可提高其射击精度。

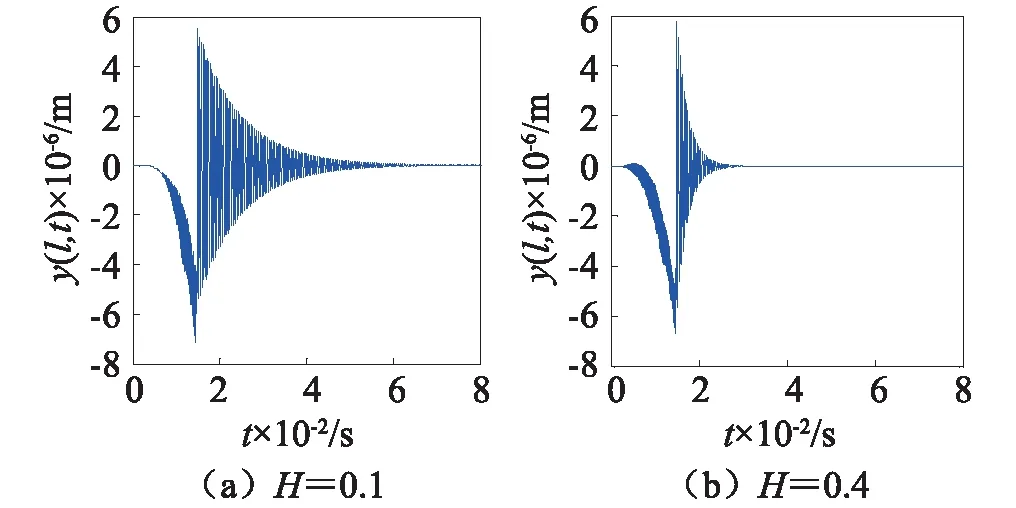
图5 弹丸有质偏时炮口振动位移Fig.5 Vibration displacement of muzzle with mass-unbalance projectile

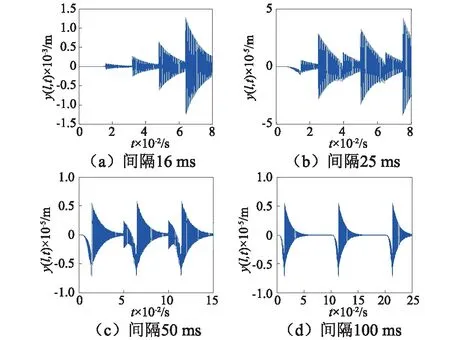
图6 弹丸有质偏时发射间隔对炮口振动的影响Fig.6 Influence of launching intervals to muzzle vibration with mass-unbalance projectile

5 结 论

针对连续射击过程中炮口的振动问题，建立了弹丸膛内加速运动作用下身管的横向振动方程；采用小参数法和迭代法，导出了弹丸连续冲击作用下身管振动方程的近似解析解。针对弹丸有、无质偏两种情形，结合试验测得的弹丸加速度，对不同身管阻尼系数、发射间隔下炮口的振动特性进行了计算，研究表明：身管阻尼系数影响炮口弹丸冲击响应的衰减速度；考虑弹丸质偏时，炮口振动幅度增大，振荡次数增多。无间隔连续射击作用下的炮口振动远大于单发射击情形，射击精度呈下降趋势；针对特定口径身管，当发射间隔大于一定值后，连续射击下炮口振动与单发射击相同。建立的连续射击过程弹丸膛内加速运动作用下身管振

动的动力学模型以及求解方法，适用于大、中、小口径舰炮连续射击时炮口的振动分析，对于确定火炮射击速度与提高火炮射击精度有重要意义。

[ 1 ] 王德石. 火炮振动理论[M]. 北京: 兵器工业出版社, 2015.

[ 2 ] 张永昌, 张相麟. 火炮身管的横向振动[J]. 兵工学报坦克装甲车及发动机分册, 1982(1): 17-23.

ZHANG Yongchang, ZHANG Xianglin. Transverse vibration of gun Barrel[J]. Acta Armamentarii, 1982(1): 17-23.

[ 3 ] 叶开沅, 马国琳. 计及行动载荷质量及惯性力影响的列车过桥动力理论[J]. 兰州大学学报(自然 科学版), 1979, 27(3): 338-352.

YE Kaiyuan, MA Guolin. Dynamical theory for vehicle-bridge considering moving loads and inertia forces[J]. Journal of Lanzhou University (Natural Science), 1979, 27(3): 338-352.

[ 4 ] 周叮, 谢玉树. 弹丸膛内运动引起炮管振动的小参数法[J]. 振动与冲击, 1999, 18(1): 76-81.

ZHOU Ding, XIE Yushu. The small parameter method for barrel vibration subjected to moving projectile[J]. Journal of Vibration and Shock，1999, 18(1): 76-81.

[ 5 ] 姜沐, 郭锡福. 弹丸加速运动在身管中激发的振动[J]. 弹道学报, 2002, 14(3): 57-62.

JIANG Mu, GUO Xifu. On the vibration of tube due to accelerately moving projectile[J]. Journal of Ballistics, 2002, 14(3): 57-68.

[ 6 ] 史跃东, 王德石. 考虑惯性效应的移动弹丸作用下身管振动特性[J]. 兵工学报, 2011, 32(4): 414-420.

SHI Yuedong, WANG Deshi. Study on vibration characteristics of barrel subjected to moving projectile considering inertia effect[J]. Acta Armamentarii, 2011, 32(4): 414-420.

[ 7 ] 朱文芳, 王育维, 魏建国, 等. 某火炮多发连续射击身管传热计算分析[J]. 火炮发射与控制学报, 2010, 31(2): 74-78.

ZHU Wenfang, WANG Yuwei, WEI Jianguo,et al. Calculation and analysis on heat transfer for a gun barrel during multiround continuous firing[J]. Journal of Gun Launch and Control, 2010, 31(2): 74-78.

[ 8 ] MICHALTAOS G, SOPHIANOPOULOS D, KOUNADIS A N. The effect of a moving mass and other parameters on the dynamic response of a simply supported beam[J]. Journal of Sound and Vibration, 1996, 191(3): 357-362.

[ 9 ] 王德石，王学军，王树宗，等.火炮振动与吸振技术研究[D].武汉：海军工程大学，2000.