基于深度学习的军用飞机部件状态参数预测

李军亮, 滕克难, 夏 菲

(1. 海军航空大学 科研部, 山东 烟台 264001；2. 92635部队， 山东 青岛 266041；3. 国网辽阳供电公司信息通信分公司，辽宁 辽阳 111000)

军用飞机是一种复杂可修系统，其状态监测数据包含了飞机、发动机和机载设备的运行信息、操纵控制变量信息、姿态信息等等。由于采集信号的传感器种类较多，采集的数据具有种类多、数据结构各异、非线性等特点，如何有效利用飞参数据对飞机关键部件的状态进行准确预测，提高飞机的使用可靠性、飞行安全性和任务成功率，是目前急需解决的难点问题。

目前状态预测的主流算法有基于可靠性理论的预测方法、基于数据驱动的预测方法和基于时效物理模型的预测方法[1-3]。基于可靠性理论的预测方法又分为寿命分布模型的预测[4]和基于故障树预测[5]的方法等；基于数据驱动的预测又分为时间序列预测[6-9]、神经网络预测[10-13]和基于滤波的预测方法[14]等；失效物理模型主要根据产品的全生命周期和失效机理知识进行产品可靠性评估[15]。现有的预测技术在理论研究和实际应用方面已经取得了较大的进步，但是，已有的预测方法也存在诸多局限，预测过程对数学模型的依赖程度大，不能满足复杂系统的实际要求，在系统的数学模型不精确时无法获得满意的结果。并且多数预测模型属于静态模型，缺乏自学习能力，预测模型通过一次建模获得，模型参数保持固定不变，没有考虑到新增样本对模型参数的影响，对于复杂装备的预测通常出现单步预测不精确、多步预测无效的问题。

2006年Hinton等[16]探讨了一种处理大数据的工具，即深度学习理论。深度学习旨在通过模拟大脑的学习过程，构建深层次的模型，结合海量的训练数据，来学习数据中隐含的特征，即利用大数据来学习特征，从而刻画数据丰富的内在信息，最终提升分类或预测的精度。目前，深度学习在语音识别、图像识别等领域的大数据分析上取得了突破性进展[17-18]。

在健康管理、故障诊断和预测方面，文献[19]采用多层RBN(Restricted Boltzmann Machine, RBM)构建一种故障诊断模型；文献[20]基于深度学习理论，设计了DAE(去噪自动编码机)为核心的针对机械设备的健康状态监测方法；文献[21]采用多层RBN来设计一种航空飞行器故障信息检测方法。论文基于军用飞机的状态信息，基于多层RBN和模拟退火算法设计了一种DBN(Deep Belief Net)方法对飞机的关键部件的监测参数的短期趋势进行预测，从而为军用飞机的健康状态评估提供依据。

1 基于深度信念网络的状态预测模型

1.1 深度信念网络模型

深度信念网络是多层网络结构，主要包括一个可见层和多层隐藏层如图1所示。可见层输入数据并且向隐含层传递数据信息完成过程学习。

深度信念网络的结构类似于多层受限制伯尔曼兹机网络(Restricted Boltzmann Machine, RBM)[22]，每一个RBM单元由两层组成，分别为隐藏层和可见层。两层之间的信息传递是受限制的，可见层到隐含层之间的数据转换由S激活函数按照RBM学习规则进行。DBN结构如图1所示，图1包括3层RBM，第一层RBM包括可见层1和隐藏层1(为第2个RBM的可见层)，第2层RBM包括可见层2(隐藏层1)和隐藏层2(为第3个RBM的可见层)，第3层RBM包括可见层3(隐藏层2)和隐藏层3(为输出层的输入数据)。

DBN中的每一个中继层都按照上述的规则进行训练数据，整个网络学习过程如图2所示。图2中，整个网络的输入数据包括：预处理的状态监测参数、网络层数、隐藏层数量、每层的神经元数量以及每层RBM单元的迭代次数。所有输入数据在网络训练之前进行初始化。

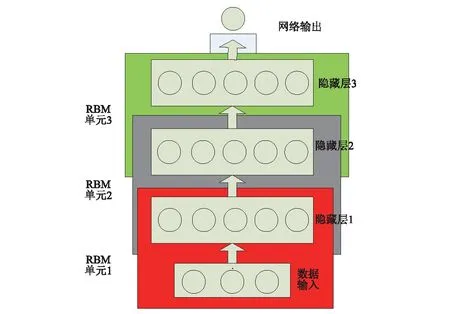
图1 深度信念网络的结构Fig.1 Deep belief network structure

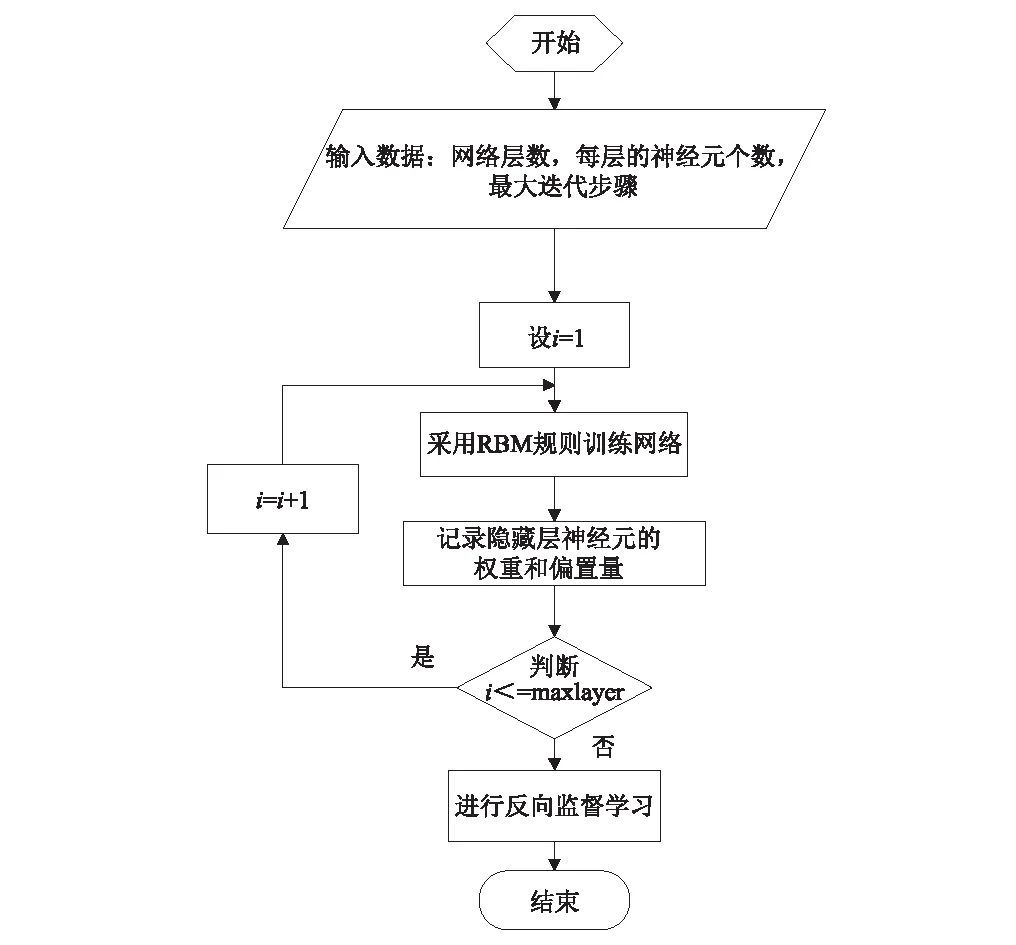
图2 深度学习网络的训练过程Fig.2 Flowchart of the DBN training process

每层RBM单元的训练过程分为两个阶段，分别为主动学习过程(Positive Learning Phase, PLD)和被动学习过程(Negative Learning Phase, NLD)，主动学习过程从最早的可见层将数据转送到隐藏层并且确定隐藏层神经元产生的概率p(h|v,W)，相反被动学习过程是上层可见单元的数据重组过程以及产生对应的概率p(v|h,W)。观测的样本数据作为向量输入到可见层，在RBM单元的训练过程中不断进行主动学习和被动学习直至满足最大迭代次数，由此确定神经元之间的权重。整个RBM的学习函数可用可见层变量v产生的概率p(v)来表示，其中v是权重和隐含层变量的函数，如式(1)所示

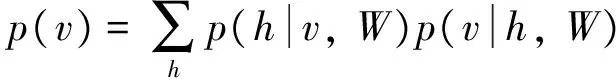
(1)

整个网络的学习过程从低层到高层逐步学习，在DBN各层学习的过程中间，各层RBN学习过程中内部独立训练权值和偏置量并存储，可以进一步分析。在训练结束之后，样本数据从第一个可见层直到通过DBN结构传递到最高阶的隐含层。

可见层和隐层之间的权重和神经元之间的偏置量通过不断迭代而进行优化，直至满足最大迭代次数。DBN各层之间的按照无监督方式学习，预测的目标模型和数据并将会在后续的监督学习过程中使用，称之为反向学习。

1.2 基于SA的DBN网络状态预测模型

本节主要讨论基于SA的DBN状态预测网络模型的实现。该模型可分为三个步骤实现，一是基于模拟退火的多层受限制的伯尔曼兹机无监督训练，二是有监督的反向传播(BP)过程，三是基于任务要求和状态信息预测算法。

(1)多层无监督学习

正如1.1节所述，DBN由多层受限制伯尔曼兹机组成，通过每个RBM单元有序的按照带有T算子的RBM规则训练完成。每个RBM由两层组成，每层由一定数量的神经元，而且同层各神经元之间无连接[23]。因此，主要的训练参数在RBM只考虑各层神经元之间权值。激活函数采用sigmiod函数，如式(2)所示

(2)

式中：si和bi分别为隐层第i个神经元的状态量和偏置量；sj为可见层第j个神经元状态量；wij为神经元i和j之间的权重；T为网络温度。

图3表示了RBM单元的迭代学习过程。在开始阶段，对各个权重和偏置量进行初始化。初始化之后，输入采集的样本对RBM单元训练。RBM隐层的神经元由可见层的神经元状态以及它们之间的权值、偏置量和激活函数确定。每次迭代过程包含两方面，主动学习和被动学习。主动学习过程将可见层输入数据转化到隐含层，被动学习是对前可见层的重新构造。这两种学习方式可用式(3)和式(4)表示

(3)

(4)

式中：hj和vk分别为隐层单元的第j个神经元和可见层的第k个神经元。式(3)为主动学习过程中的隐层神经元状态，由激活函数确定，式(4)为被动学习过程可见层神经元的状态。可见层和隐层的神经元按概率随机取值0或者1，代表链接或者断开状态。

(5)

式中：δ在0～1取值，代表学习速率；〈vkhj〉data为主动学习之后的隐层第j个神经元和可见层的第k个神经元之间的状态变量；〈vkhj〉recon为被动学习之后可见层的重组神经元的状态向量。偏置量也按照相同规则迭代。为了使学习过程更加稳定，变量m被用来更新权重和偏置量。权重的变化量Δwjk，当前迭代过程和先前跌过步骤可用式(6)表示

(6)

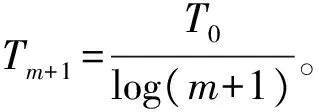
在DBN学习过程权值和偏置量中不断迭代优化，通过各个RBM单元的迭代实现DBN网络的训练。

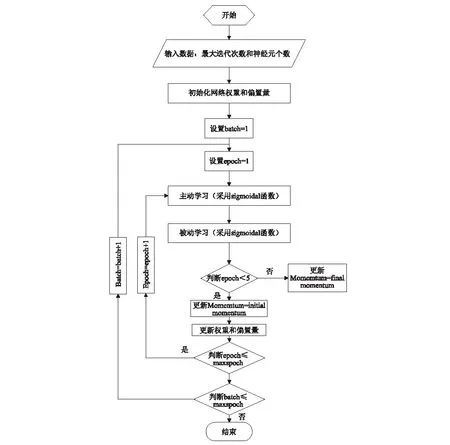
图3 RBM单元的迭代学习过程Fig.3 Iterative learning of RBM unit

(2) 反向有监督学习

在进行完各个RBM单元的学习之后，要进行有监督的学习，通过反向神经网络训练算法来完成。监督学习算法可以进一步减少训练误差提高网络的预测精度。有监督的学习通过使用分类数据进行DBN模型训练。和无监督学习的不同只考虑一个RBM单元，反向DBN同时考虑所有的RBM单元。训练误差由训练模型输出数据和分类目标数据计算得出。DBN模型的各项参数不断更新以使得误差最小，直至达到最大迭代次数。在进行DBN的反向训练之后再通过微调算法对整个网络参数进行为微调。文中采用共轭梯度算法进行微调。

(3)军用飞机部件状态参数预测

军用飞机执行不同任务包含不同的任务剖面，不同任务剖面对应不同的放飞标准，不同放飞标准对应不同最小设备清单，不同设备清单对应不同的技术状态。因此针对不同任务应当有针对性的提高对应部件的可靠性，从而遂行作战任务。某型飞机作战任务的任务剖面和装备状态的对应关系如表1所示[24]。

表1 飞机任务剖面与飞机各系统设备状态关系

表1中，s-1代表动力系统，s-2代表燃油系统，s-3代表液压系统，s-4代表冷气系统，s-5代表操纵系统，s-6代表飞控系统，s-7代表起落装置，s-8代表生命保障系统，s-9代表电源电气系统，s-10电子对抗系统，s-11代表武器系统,s-12代表发控系统。

根据以上分析，设计基于任务要求和状态信息的部件参数信息预测方法，具体步骤如下：

步骤1 对作战任务进行分析，根据作战任务包含的任务剖面确对应的关键部件可用集合S表示，S=(S1, …Si, …,Sn)，其中Si为第i个系统，Si=(s1, …sj, …,sn)，sj为i个系统里的第j个部件；

步骤2 分析关键部件的主要特征参数，进一步确定需要采集的相关状态信息Xi=(x1, …xj, …,xn)，Xi为第i个部件的状态信息集；

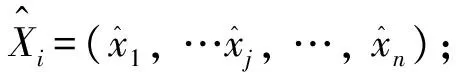
步骤4 按照1.2节的(1)和(2)部分对DBN网络训练；

步骤5 用已知数据对DBN网络进行验证；

步骤6 用已监测到的飞参数据作为输入向量，对未来状态信息进行预测；

步骤7 通过预测出的状态信息，判断关键部件的健康状态。

根据以上分析可知，基于SA和DBN的军用飞机状态参数预测流程可如图4所示。

图4中，基于SA和DBN的网络结构和运算过程由图2和图3所示的流程实现。

2 案例分析

假定某次执行任务包含剖面p-4，各系统的完好情况如表1第5行所示，在此以动力系统为例对其健康状态进行分析。

首先通过1.2节(3)部分设计的方法选定发动机状态检测参数，进而设计网络输入样本。

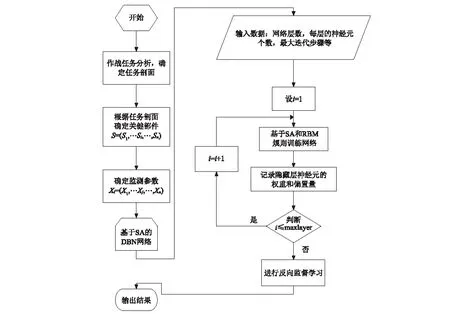
图4 基于SA和DBN的军用飞机状态参数预测流程Fig.4 Military aircraft components state parameterprediction Process based on SA and DBN

航空发动机的状态监测参数主要包括[25-26]：气路监测、滑油监测和振动监测三部分，具体参数有涡轮后燃气温度、燃油流量、滑油的压力、滑油温度、滑油消耗率、低压转子振动值偏差和高压转子振动值偏差等。

论文以某型发动机为例进行状态预测，该发动机主要监测数据有发动机扭矩、发动机转速、排气温度发动机滑油压力、滑油温度和燃油瞬时流量等参数。

其数据来源为该型机的飞参数据系统，飞行参数系统是对飞机在飞行过程中，对飞行操纵量、姿态量、飞行环境参数、部(附)件监测信息等状态信息的综合信息系统[27]，可以为论文的数据采集工作提供有力支撑(见图5)。

图5 飞参信息系统Fig.5 Aircraft flying parameter information system

按照1.2节(3)设计的方法，将飞参系统采集监测数据信息记为X=(x1,x2, …,x6)，分别代表发动机扭矩、发动机转速、燃气温度发动机滑油压力、滑油温度和燃油瞬时流量。

人工神经网络具有并行处理、联想记忆、分布式知识存贮、强鲁棒性等特点，在非线性系统的辨识和控制中得到了广泛应用，其中ELMAN神经网络在系统预测方面有较多的工程应用，分别实现了空调负荷、地震等级预测、交通运输能力预测和电力系统负荷预测等问题[28-29]；支持向量机是基于统计学习理论构建的典型神经网络，在故障诊断和预测方面也有较好的应用[30-32]。

为了验证文中设计方法的精确性和快速收敛性，分别采用SVM、ELMAN和深度网络对表2中的样本训练网络。将表2中每70组数据作为一组输入，对第71的数据进行预测，即第1～70组为输入数据，第71～100组为训练目标，表中共有1 000组数据，其中第1～900组数据作为训练样本，第900～1 000组作为测试数据。

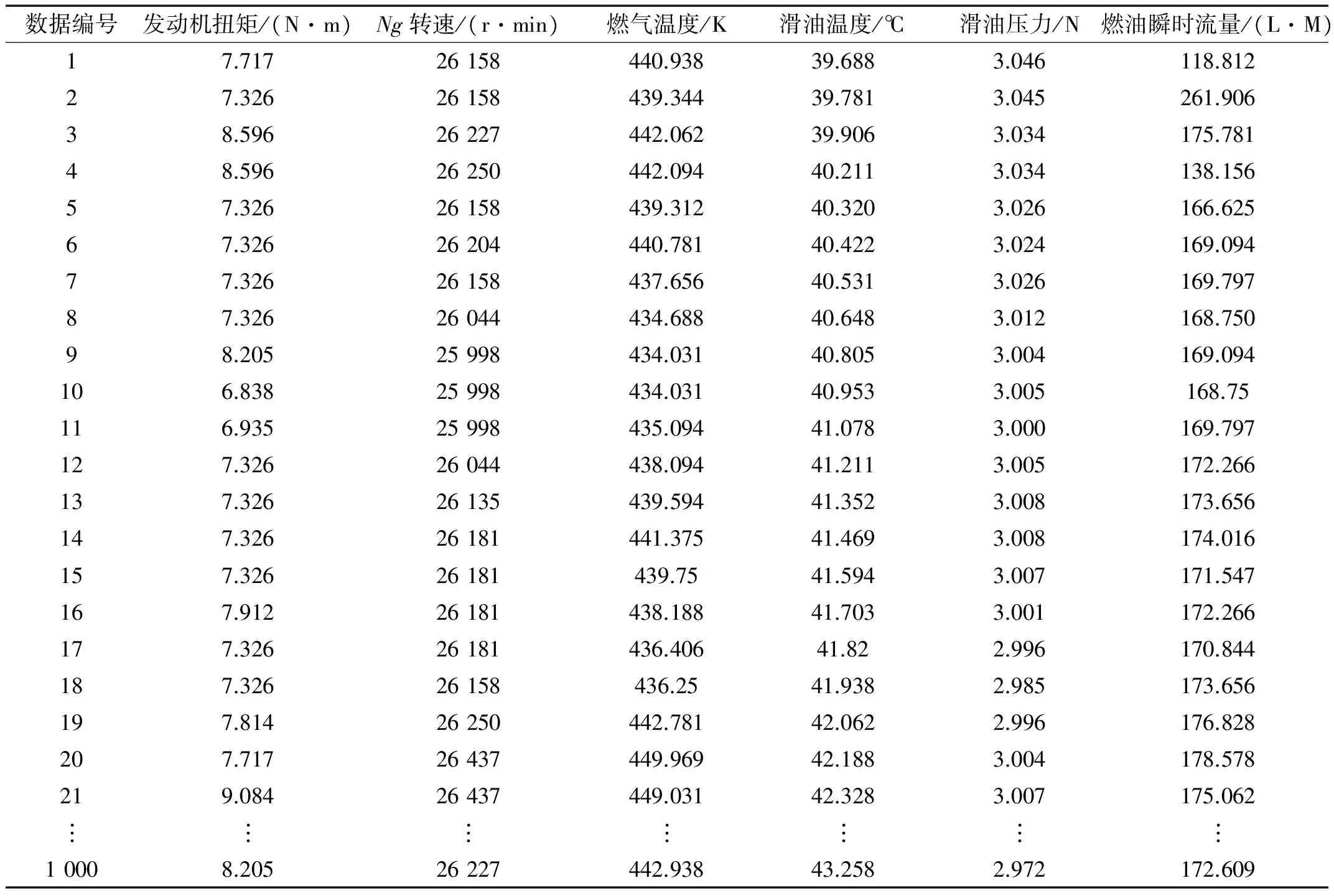
表2 样本数据

DBN算法中的参数由第1节设计方法确定，RBN选择4层，输入层和输出层神经元为6个，隐藏层每个神经元数量为100，在每个RBM和反向学习过程中的最大迭代步骤设为50；ELMAN网络的输入和输出层激活函数“tansig”和“purelin”，根据kolmogorov定理确定Elman网络隐藏层神经元数量；SVM采用高斯核函数。

采用matlabR2010编程实现，在配置为Windows-7旗舰版windows-32系统，inter(R) core i3-200CPU，3.10 Hz, RAM4.0 GB的计算机上运行程序，当参数预测结果和实测结果之差小于0.04时，认为预测结果正确，计算测试数据的预测值和实测值的正确率如表3所示。

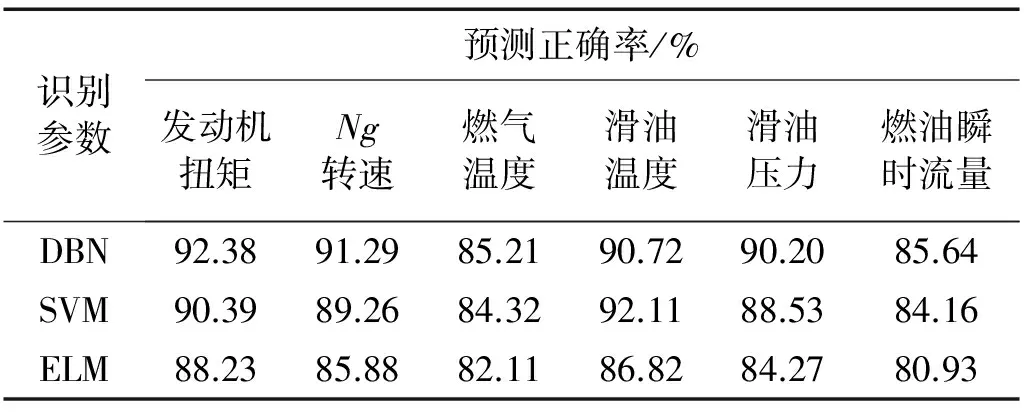
表3 不同算法的预测结果对比

由表3可知，DBN算法的预测精度最高，SVM次之，ELM预测精度最低。在DBN网络中，RBN单元是一种随机概率网络，在网络训练过程中模拟了样本数据的概率分布特性，另外通过模拟算法通过T的控制作用，使得网络权值梯度(各层之间能量差)有规律的降低，不容易使网络陷入局部最优，提高训练精度。

在此采取DBN算法对发动监测参数进行预测，来对发动的状态信息分析，以表2中的第900～970组数据为样本数据，输入数据维数为70×6，输出维数为6，通过第901～970组数据预测第971组，并且将预测结果作为新的971组，用第902～971组预测第972组，以此类推，预测步长设定为30，对未来各项状态信息进行预测，其结果如图6～图11所示。

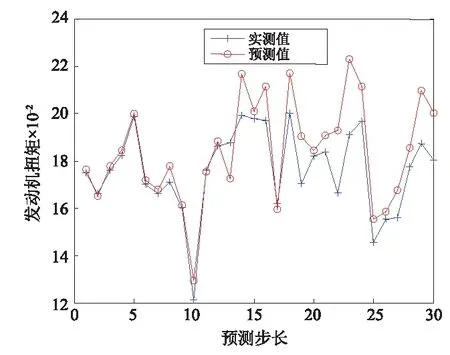
图6 发动机扭矩预测Fig.6 The prediction value of engine torque

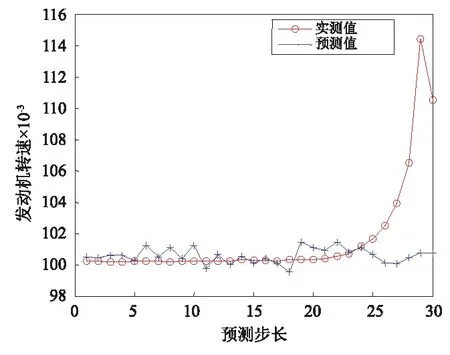
图7 发动机转速预测值Fig.7 The prediction value of engine rotate speed

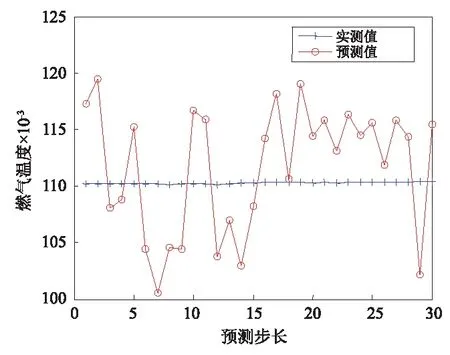
图8 发动机燃气温度Fig.8 The prediction value of engine jet temperature

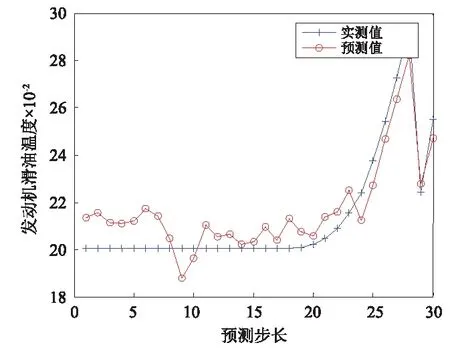
图9 发动机滑油温度Fig.9 The prediction value of engine lubricating oil temperature

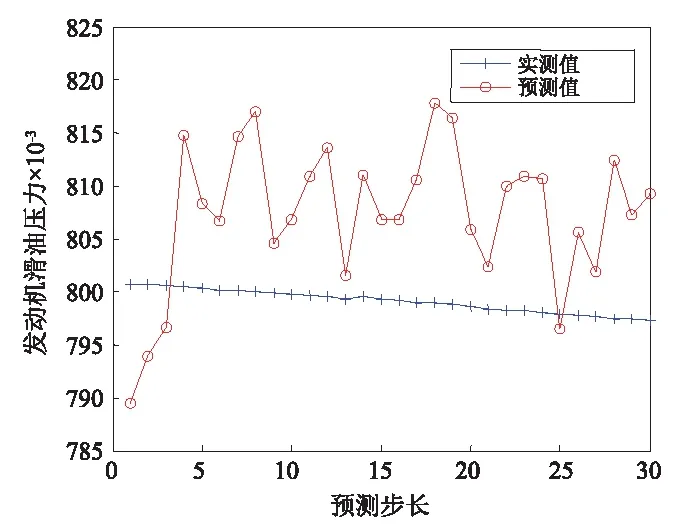
图10 发动机滑油压力Fig.10 The prediction value of engine lubricating oil pressure

图11 发动机燃油瞬时流量Fig.11 The prediction value of engine fuel instantaneous flow

图6、图7、图9和图11中预测数值与实测值走势一致，且误差小于0.02，图8和图10中，发动机燃气温度和滑油压力的预测数值的趋势与实测值不太一致，波动较大，有出现故障的征兆，应当重点监控，在维修过程中对相应的部件系统加强检查。

3 结 论

文章设计方法可以有效预测军用飞机关键部件的状态参数信息，状态参数预测的正确率高于SVM和ELMAN网络，预测误差小于0.04。证明深度网络可以实现对复杂系统状态信息的多步预测，且预测精度较高。该方法在工程上有较强的应用性，预测结果可以作为军用飞机部件可靠性分析和制定预防性维修计划的参考依据。同时，也是深度学习理论在健康管理研究领域的进一步探索。

[ 1 ] 彭宇, 刘大同. 数据驱动故障预测和健康管理综述[J].仪器仪表学报, 2014, 35(3)： 481-495.

PENG Yu, LIU Datong. Data-driven prognostics and health management: a review of recent advances[J]. Chinese Journal Scientific Instrument, 2014, 35(3)： 481-495.

[ 2 ] 李向前. 复杂装备故障预测与健康管理关键技术研究[D]. 北京: 北京理工大学, 2014: 6-12.

[ 3 ] 王少萍. 大型飞机机载系统预测与健康管理技术[J]. 航空学报, 2015, 35(6): 1459-1472.

WANG Shaoping. Prognostics and health management key technology of aircraft airborne system[J]. Acta Aeronautica et Astronautica Sinica, 2015, 35(6): 1459-1472.

[ 4 ] 赵宇.可靠性数据分析[M]. 北京: 国防工业出版社, 2011: 33-55.

[ 5 ] 周忠宝, 马超群, 周经伦. 基于动态贝叶斯的动态故障树分析[J]. 系统工程理论与实践， 2008, 32(2): 36-42.

ZHOU Zhongbao, MA Chaoqun. Dynamic fault tree analysis based on dynamic Bayesian networks[J]. Systems Engineering Theory &Practice, 2008, 32(2): 36-42.

[ 6 ] MIRIKITANI D T，NIKOLAEV N. Recursive bayesian recurrent neural networks for time-series modeling[J]. IEEE Transactions on Neural Networks, 2010， 21(2): 262-274.

[ 7 ] ZHAO W G，WANG J Z, LU H Y. Combining forecasts of electricity consumption in China with time-varying weights updated by a high-order Markov chain model[J]. Journal of Management Science, 2014, 45: 80-91.

[ 8 ] SAPANKEVYCH N，SANKAR R. Time series prediction using support vector machines: a survey[J]. Computational Intelligence Magazine, 2009, 4(2): 24-38.

[ 9 ] 徐圆，刘莹，朱群雄. 基于多元时滞序列驱动的复杂过程故障预测方法应用研究[J]. 化工学报, 2013，64(12): 4290-4295．

XU Yuan, LIU Ying, ZHU Qunxiong. A complex process fault prognosis approach based on multivariate delayed sequences[J]. CIESC Journal, 2013, 64 (12): 4290-4295.

[10] MIRIKITANI D T，NIKOLAEV N. Recursive bayesian recurrent neural networks for time-series modeling[J]. IEEE Transactions on Neural Networks，2010，21(2): 262-274.

[11] GONCALVES L F，BOSA J L，BALEN T R，et al. Fault detection, siagnosis and prediction in electrical valves using self-organizing maps[J]. Journal of Electronic Testing, 2011, 27(4): 551-564.

[12] 张琪, 吴亚锋, 李锋. 基于遗传神经网络的旋转机械故障预测方法研究[J]. 计算机测量与控制, 2016, 24(2): 11-13.

ZHANG Qi, WU Yafeng, LI Feng. Research on mechanical fault prediction based on improved neural network[J]. Computer Measurement & Control, 2016, 24(2): 11-13.

[13] 李瑞莹, 康锐. 基于神经网络的故障率预测方法[J]. 航空学报, 2008, 29(2): 357-362.

LI Ruiying, KANG Rui. Failure rate forecasting method based on neural networks[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(2): 357-362.

[14] 张磊，李行善，于劲松. 一种基于二元估计与粒子滤波的故障预测算法[J]. 北京航空航天大学学报, 2008, 34(7): 798-802.

ZHANG Lei, LI Xingshan, YU Jinsong. Fault prognostic algorithm based on dual estimation and particle filter[J]. Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(7): 798-802.

[15] 蔡志强, 孙树栋, 司书宾, 等. 基于FMECA的复杂装备故障预测贝叶斯网络建模[J]. 系统工程理论与实践, 2013, 33(1): 187-192.

CAI Zhiqiang, SUN Shudong, SI Shubin, et al. Modeling of failure prediction bayesian network based on FMECA[J]. Systems Engineering Theory &Practice, 2013, 33(1): 187-192.

[16] HINTON G E，SALAKHUTDINOV R R. Reducing the dimensionality of data with neural networks[J]. Science， 2006， 313 ：504-507.

[17] AREL L, ROSE D C, KARNOWSKI T P. Deep machine learning a new frontier in artificial intelligence research[J]. Computational Intelligence Magazine, 2010, 5(4): 8-13.

[18] 郭丽丽, 丁世飞. 深度学习研究进展[J]. 计算机科学, 2015, 42(5): 28-33.

GUO Lili, DING Shifei. Research progress on deep learning[J]. Computerscience, 2015, 42(5): 28-33.

[19] PRASANNA T, PINGFENG W. Failure diagnosis using deep belief learning based health state classification[J]. Reliability Engineering and System Safety, 2013, 115(7): 124-135.

[20] 雷亚国, 贾峰, 周昕, 等. 基于深度学习理论的机械装备大数据健康检测方法[J]. 机械工程学报， 2016, 51(21): 49-56.

LEI Yaguo, JIA Feng, ZHOU Xin, et al. A deep learning-based method for machinery health monitoring with big data[J]. Journal of Mechanical Engineering, 2016, 51(21): 49-56.

[21] 冯通. 基于深度学习的航空飞行器故障自助检测研究[J]. 计算机仿真, 2015, 32(11): 119-122.

FENG Tong. A fault detection algorithm of aviation aircraft based on deep learning[J]. Computer Simulation, 2015,32(11): 119-122.

[22] HINTON G E. A practical guide to training restricted Boltzmann machines[J] . Momentum, 2012, 9(1): 599-

619.

[23] LEE H, GROSSE R, NG A Y. Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations[C] ∥International Conference on Machine Learning. Montreal: ICML, 2009: 609-616.

[24] 王利民，马乃仓. 军用飞机最低技术放飞条件逻辑决断分析方法研究[J]. 计算机与现代化, 2012 (10): 200-206.

WANG Limin, MA Naicang. Study on logic decision method of making military aircraft minimum technique flight condition[J]. Computer and Modern, 2012 (10): 200-206.

[25] 孙闯，何正嘉，张周锁，等. 基于状态信息的航空发动机运行可靠性评估[J]. 机械工程学报, 2013, 49(6): 30-37.

SUN Chuang, HE Zhengjia, ZHANG Zhousuo， et al. Operating reliability assessment for aero-engine based on condition monitoring information[J]. Journal of Mechanical Engineering, 2013, 49(6): 30-37.

[26] 王华伟，高军，吴海桥. 基于竞争失效的航空发动机剩余寿命预测[J]. 机械工程学报, 2014, 50(6): 197-205.

WANG Huawei, GAO Jun, WU Haiqiao. Residual remaining life prediction based on competing failures for aircraft engines[J]. Journal of Mechanical Engineering, 2014, 50(6): 197-205.

[27] 唐崇凯, 曲建岭，高峰. 飞参判据及应用[J]. 计算机工程, 2011, 37(10): 280-283.

TANG Chongkai, QU Jianling, GAO Feng. Flight data criterion and its application[J]. Computer Engineering, 2011, 37(10): 280-283.

[28] 李军亮, 胡国才. 基于ELMAN网络的某型直升机飞行状态识别[J]. 火力与指挥控制，2015, 40(12): 57-60.

LI Junliang, HU Guocai. Helicopter flight condition recognition based on elman neural network[J]. Fire Control & Command Control, 2015, 40(12): 57-60.

[29] 李国勇，杨丽娟. 神经, 模糊, 预测控制及其MATLAB 实现[M]. 北京：电子工业出版社， 2013: 85-127.

[30] 徐玉秀, 杨文平, 吕轩, 等. 基于支持向量机的汽车发动机故障诊断研究[J]. 振动与冲击, 2013, 32(8): 143-146.

XU Yuxiu, YANG Wenping, LÜ Xuan, et al. Fault diagnosis for a car engine based on support vector machine[J]. Journal of Vibration and Shock, 2013, 32(8): 143-146.

[31] 袁胜发, 储福磊. 支持向量机及其在故障诊断中的应用[J]. 振动与冲击, 2007, 26(11): 29-35.

YUAN Shengfa, CHU Fulei. Support vector machine and its application in machine fault diagnosis[J]. Journal of Vibration and Shock, 2007, 26(11): 29-35.

[32] 陈昌，汤宝平，吕中亮. 基于威布尔分布极最小向量机的滚动轴承退化趋势预测[J]. 振动与冲击, 2014, 33(2): 52-56.

CHEN Chang, TANG Baoping, LÜ Zhongliang. Degradation trend prediction of rolling bearings based on weibull distribution and least squares support vector machine[J]. Journal of Vibration and Shock, 2014, 33(2): 52-56.