考虑弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励动力学建模

剡昌锋, 康建雄, 苑 浩, 吴黎晓, 韦尧兵(兰州理工大学 机电工程学院，兰州 730050)

滚动轴承是旋转机械重要的部件之一，它广泛应用于化工、冶金、航天等重要部门。滚动轴承在长期的运转过程中，其内、外圈表面会产生裂纹、点蚀或剥落等局部缺陷，这是滚动轴承产生振动、噪音和疲劳破坏的主要因素之一。弹流润滑油膜可以承受较高的油膜压力，因此润滑会使接触刚度发生变化，对轴承的载荷—变形曲线关系产生影响。滚动轴承运转时要使滚动体在滚道上纯滚动，滚动体必须与滚道之间有足够大的摩擦力；否则滚动体就会在滚道上滑动。当润滑存在时，较小的摩擦力会使滚子发生滑动加速了滚动轴承的磨损。动力学分析模型不仅可有效分析轴承的载荷和转速随时间变化时的工作状态等，而且能更真实准确地描述轴承动态响应特征。为确保旋转机械安全、平稳高速地运转，降低振动和噪声水平；开展滚动轴承故障动力学建模及其相应分析研究，对进一步认识滚动轴承的接触振动机理是十分重要的。

Jones[1]首先提出滚动轴承拟静力学分析方法。采用套圈控制假设，分析了接触界面的滑移、球的运动和滑动摩擦。Gupta等[2]系统地分析了轴承各个零件之间的相互作用，通过数学模型对轴承各部件相互间的振动响应进行了研究。Liao等[3]建立了高速球轴承的拟动力学模型,研究了球轴承的载荷分布规律，离心力、接触角、钢球旋滚率等变化规律，研究了高速球轴承的热力耦合特性和温度场分布规律，提出了高速球轴承疲劳寿命预测的新方法。Kulkarni 等[4]建立了滚动轴承外滚道局部缺陷动力学模型，对外滚道表面的单缺陷角位置、缺陷尺寸、载荷力和多故障等不同条件下的振动影响分别进行了研究。Patil等[5]建立了2自由度的滚动轴承动力学模型，研究了滚道表面局部缺陷大小、缺陷位置对轴承动态性能的影响规律。Patel等[6]建立内、外圈表面存在多个表面缺陷的深沟球轴承动力学模型，采用龙格库塔法求解耦合运动控制方程，分析含表面缺陷的保持架、套圈和球的瞬时振动频率。Shao等[7]以Hertz接触理论为理论基础，建立滚动体与内外圈滚道之间非理想Hertz接触特性和时变位移激励的圆柱滚子轴承局部缺陷动力学模型。Petersen等[8]分析了双列滚动轴承滚道局部缺陷载荷分布及刚度对轴承运转的影响，结果表明当滚动体经过缺陷位置时，其承载能力消失或者减小，载荷重新分配到其它滚动体上，承载区的刚度减小，非承载区的刚度增大。刘静等[9]考虑了不同形貌特征的缺陷以及对于裂纹缺陷在轴承运转中缺陷的演变，并建立了非线性赫兹线接触特性和时变位移激励的圆柱滚子轴承局部缺陷动力学模型。曹宏瑞等[10]考虑了旋转内圈离心膨胀和热膨胀变形对轴承内部几何位移的影响，并改进了Jones提出的模型，研究了静载荷、动态载荷及高转速等工况下滚动轴承内部接触载荷、接触位置的变化规律，并基于材料疲劳失效理论对轴承的损伤机理和早期损伤部位进行了分析。Wijnant等[11]研究了不同载荷及不同接触角下椭圆接触润滑对于轴承的影响，同时研究了阻尼变化对于轴承的影响。Wiegert等[12]提出了简化的弹性流体动力学模型，适合研究弹性流体动力学及赫兹接触力等。Liao等[13]考虑离心力的影响，通过球轴承的几何分析和力平衡分析，获得了球的接触力和接触角，研究球轴承在径向和轴向载荷同时作用下的打滑行为。张亚洲等[14]引入了滚动体的随机滑动和周期性变化的振动传递函数, 并综合考虑了静态载荷分布和故障点的位置, 建立了滚动轴承局部故障的随机振动数学模型。Bastami等[15]提出一种新的滚动轴承模型，该模型考虑了无故障轴承以及有故障轴承的随机激励。主要研究了粗糙接触表面产生的随机频带，随机接触力是产生随机噪声的过程。Sawalhi等[16]对齿轮箱轴承建立了动力学模型，提出齿轮箱轴承滚动体滑动的一般模型，并模拟了齿轮箱轴承局部缺陷时的动力学响应。Patil等[17]对轴-轴承系统建立了球轴承存在多点蚀的2自由度多体动力学模型，提出了滚动体的接触力计算考虑非线性赫兹接触变形和内部径向间隙，并列出内圈、外圈、滚动体有缺陷时的方程研究轴承的动态响应。剡昌锋等[18]考虑了滚动轴承弹流润滑对于轴承运转的影响，将接触变形、径向间隙和缺陷的连续性变化关系对轴承的局部缺陷影响，并建立深沟球轴承的2自由度动力学模型，能更加准确的模拟轴承实际运转时的真实状态。康建雄等[19]在文献[18]基础上加入滑动这一因素，采用随机函数表示滚动体滑动的特性，建立了轴承局部缺陷的动力学方程。

以上研究考虑了轴承内外圈滚道、轴承载荷分布、缺陷大小等因素在纯滚动状态下动力学响应特性。忽略了轴承座、弹流润滑下油膜及滑动的综合影响。随着轴承向高精度发展，轴承座、弹流润滑、滑动对轴承运转有不可忽视作用。本文在考虑了弹流润滑、滚道外圈缺陷、滑动和轴承座对滚动轴承运转所产生的影响，以深沟球轴承为研究对象，研究缺陷大小、滑动和轴承转速等对轴承的振动响应特性影响。

1 建立动力学模型

本文以赫兹接触理论为基础，建立滚动轴承系统局部缺陷位移激励2自由度动力学模型。为研究滚动轴承系统局部缺陷振动响应，将滚动体元素与滚道之间的接触简化为质量-弹簧-阻尼模型。

1.1 滚动轴承系统简化模型

假设外圈与轴承座之间界面为弹性连接，内圈与转轴之间为刚性连接，滚道和滚动体间的接触为非线性接触且满足赫兹接触理论。滚动轴承系统简化模型如图1所示，其中p为轴承座，O为轴承外圈，I为轴承内圈。

图1 滚动轴承系统简化模型示意图

根据Hertz接触变形理论，非线性载荷-位移关系为

(1)

式中：F为载荷-位移系数；δn为径向位移。

1.2 滚动体与滚道接触刚度计算

滚动体与滚道的接触刚度用下式计算

(2)

1.3 径向变形的计算

在θi角度时第i滚动体和滚道之间的接触变形δi如图2所示

δi=xsinθi+ycosθi-Cγ

(3)

式中：Cγ为径向间隙；θi为第i个滚动体与滚道之间的接触角。

(4)

式中：Z为滚动体总数、i为滚动体号数、ωc为保持架角速度，θ0为相对于y轴的第一个球的初始角位置。

保持架的角速度

(5)

图2 接触变形关系

2 计算油膜厚度和刚度

温度和压力分布会影响油膜厚度的计算，在此研究中假定温度及其压力恒定，对油膜刚度和阻尼系数进行计算。由于润滑油可以承受较高的压力，因此滚动体与滚道接触面的接触刚度会发生变化，进而影响到轴承的载荷——变形曲线。

2.1 最小油膜厚度计算

最小油膜厚度就是等效滚动体接触表面出口区隆起处与相对接触平面间的油膜厚度。在理论分析与实验研究的基础上，Dowson等[20]在实验与理论分析的基础上提出最小油膜厚度的计算公式

(6)

该公式常用于线接触润滑状态下最小油膜厚度的计算，随后Hamrock等[21]随后推导了椭圆点接触最小油膜厚度更为普遍的计算公式

(7)

油膜接触区中心油膜厚度可近似表示为

(8)

2.2 油膜刚度计算

(9)

式中：Q为径向载荷；E*为两接触体的等效弹性模量。

根据刚度的定义，由式(7)、(8)和(9)可求得油膜刚度为

(10)

滚动体与滚道相对滚动的同时产生挤压，整个接触区可以分为入口区、赫兹接触区、出口区三部分。由于接触副的低阻尼性，在Hertz接触区的油膜阻尼可以忽略。赫兹接触区刚度计算由式(2)计算求得，阻尼CS为100 Ns/m。出口区油膜气穴形成的负压对于接触特性的影响很小，所以将其影响忽略不计。

2.3 入口区油膜刚度和阻尼

计算入口区的油膜法向载荷Qr时，需要考虑润滑剂的卷吸和挤压运动。根据文献[22]得到入口处油膜载荷：

(11)

式中：a为接触椭圆的长半轴轴长，ux为球与滚道的卷吸速度，uz为振动速度，ηo为润滑剂黏度。

则入口区的刚度及阻尼为[23-24]

(12)

(13)

油膜刚度、赫兹接触刚度、入口处油膜接触刚度之间的关系简化示意图如图3所示，接触总刚度按串联与并联关系计算。

图3 接触副弹簧阻尼模型

3 表面局部缺陷及其附加位移

为了便于研究，将轴承缺陷形貌特征定义为矩形小缺陷情形，内外滚道缺陷长(L)、宽(B)、深(D)一致。滚动体与缺陷滚道接触过程如图4所示。图4(a)为球刚进入缺陷时的接触状态，(b)为球完全进入缺陷时的接触状态，(c)为球离开缺陷时的接触状态，(d)为缺陷尺寸较大时球进入缺陷到离开的接触状态。从图4(a)、(b)、(c)可以看出球从进入缺陷到离开缺陷的过程中接触情况。图4(d)为缺陷演变的比较复杂一个过程，即随着缺陷的增大球会运动到缺陷底部再离开缺陷。

(a)(b)(c)(d)

图4 球经过缺陷时接触状态

Fig.4 Different condition of ball passing defect

滚动体经过轴承局部缺陷时，会产生接触变形以外的附加位移。考虑缺陷尺寸小于球直径，滚动体与缺陷底部不发生碰撞，则滚动体经过缺陷的附加位移Hf可以表示为

(14)

式中：∅q为缺陷角，Hmax为最大附加位移，∅di为滚动体相对于Y轴的角位置、∅0为缺陷初始角。

如图5所示，缺陷较小的情况下，缺陷角可表示为

图5 缺陷角与角位置关系

(15)

式中：r为外滚道半径。

(16)

根据滚动轴承位移几何关系，得到：

(17)

式中：d为滚动体直径。

当缺陷存在时是会产生附加位移Hf，故球经过缺陷滚道时产生的接触位移量

δ=xsinθi+ycosθi-(Cγ+Hf)

(18)

4 轴承滑动

滚动体与滚道接触运动时，受惯性力的影响会造成两接触件之间存在线速度差异，此时轴承滚动体与滚道会产生滑动。由于线速度差异不明确滚动体相对于滚道在正常运转情况下会提前或者延后，导致滚动体产生向前或向后运动。将滑动的区域用角度θslip表示，采用均匀分布函数φ表示滑动时滚动体相对于滚道的位置。产生滑动时第球和滚道之间的接触角就可以表示为

(19)

用[-θslip，θslip]上均匀分布函数表示φ，根据经验在滚动轴承中，θslip的范围为(0.01～0.02)rad。

5 建立局部缺陷动力学方程

根据简化的模型轴承系统由质量块M、阻尼C、弹簧K组成的模型。当轴承产生局部缺陷时，其接触位移δ的变化使接触力发生变化。根据牛顿第二定律，质量引起的惯性力、阻尼引起的阻尼力及接触变形引起的接触力与外力平衡。以X轴及Y轴为横纵方向，轴承在两个方向的位移建立2自由度局部缺陷轴承系统位移激励数学模型并列出动力学方程

βHf)]3/2sinθi=Wx

(20)

βHf)]3/2sinθi=Wy

(21)

β是判断球与滚道是否发生接触的参数，表示为

(22)

6 模拟模型及实验验证

6.1 局部缺陷模型无滑动轴承振动响应

为验证所建立模型的正确性，分别对无缺陷和内、外滚道产生局部缺陷的SKF6205深沟球轴承进行模拟。局部缺陷长度(L)、宽度(B)、深度(D)均为0.177 8 mm。采用西储大学的轴承数据来验证所建模型。试验深沟球轴承型号与模拟轴承型号、缺陷大小完全相同，轴承外圈固定，转子的转速1 750 r/min (≈29.17 Hz)。试验使用加速度传感器采集振动信号，安装在电机壳体驱动端 12点钟位置，以12 000 S/s的采样速率采集信号。实验台如图6所示。

图6 凯斯西储大学试验台

SKF 6205轴承的参数，见表1。

为了获得轴承动态特性，采用四阶龙格库塔法对式(20)和(21)进行求解。选取步长为Δt=1×10-4s，x和y方向位移初始值分别为x0=10-6m和y0=10-6m。表2为系统转频(fs)、内滚道故障频率(fbpi)和外滚道故障频率为(fbpo)在1 750 r/min时理论计算值。

图7(a)为无故障轴承模拟信号时域图，(b)为图(a)通过快速傅里叶变换得到的频域图。时域图中可以看出模拟信号比较平稳，无较大的冲击成分出现。从频谱图中可以看出轴承运转初期频率变化比较明显，这与实际轴承运转情况相符合。同时频谱图中包含轴承转频(fs)及其二倍频等，转频为28.08 Hz。

表1 SKF 6205深沟球轴承参数

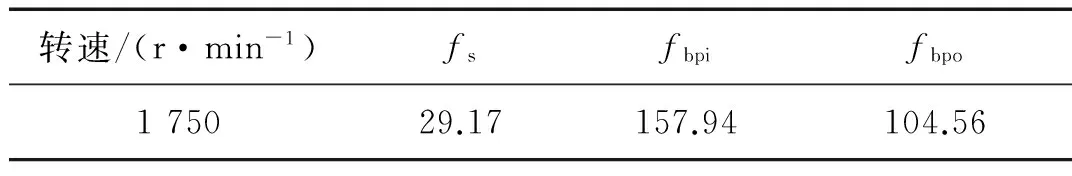
表2 转频、内圈和外圈故障频率理论值

图8(a)和(b)为无故障实验时域及频域图。从图8(a)中看出原始信号中有些轻微的冲击成分，这可能是由于实验中轴承安装引起的不对中、运行环境噪声等的影响。对原始信号进行降噪、包络分析后得到频谱图8(b)。从中可以看出实验数据处理后轴承转频和二倍频同样存在，转频为30.42 Hz。对图7(b)与图8(b)进行比较可以看出转频及其二倍频等频率值基本吻合，但是幅值有偏差。这是因为实验数据是真实环境下进行测试的，而其频域图是经过降噪处理以后得到的，因此会有较大的差异。

滚动轴承内圈存在缺陷时，对轴承的正常运转存在较大的影响。图9(a)和(b)为内滚道存在局部单个缺陷模拟时域及频域信号图，从图9(a)中可以看出周期性的冲击信号。图9(b)为图9(a)通过快速傅里叶变换得到的频谱图，从图中可以看出内圈故障转频(28.08 Hz)、特征频率(158.1 Hz)及其二倍频(2fbpi)、特征频率边频带(fbpi-fs、fbpi+fs)。边频带主要由转频的调制产生，特征频率值为158.1 Hz。图9(b)中可以看到主频上幅值比边频带大很多，原因是在低速情况下模拟信号比较稳定，没有其他成分的干涉。图10(a)、(b)为实验信号时域及频域图，图10(a)中明显的可以看出周期性的冲击成分；对其进行降噪后包络分析得到频谱图，频域图中同样包含转频(29.16 Hz)、特征频率(156.6 Hz)及边频带。对实验数据与模拟数据进行比较，可以看出模拟模型数据与实验数据特征频率值基本吻合。

(a) 无故障模拟信号时域图

(b) 无故障模拟信号频域图

(a) 实验无故障时域图

(b) 实验无故障频域图

(a) 轴承内圈故障模拟时域图

(b) 轴承内圈故障模拟频域图

图11(a)和(b)为外滚道存在单个故障模拟时域图和频域图。从图中可以看出当外圈存在缺陷时，时域图中同样出现周期性冲击现象；频域图中出现故障特征频率(104.4 Hz)和特征频率的二倍频(208.7 Hz)等。图11(b)没有边频带是因为外圈与轴承座固定，转频对外圈就不存在频率的调制。图12(a)和(b)为外滚道存在故障实验时域、频域图。时域图中可以清晰地看到冲击信号呈周期性变化，对时域图12(a)经过降噪处理后得到图12(b)，图12(b)中同样有特征频率(104.8 Hz)与二倍频(209.7 Hz)等。

(a) 轴承内圈故障实验时域图

(b) 轴承内圈故障实验频域图

Fig.10 Fault simulation time domain and frequency domain of bearing inner race

(a) 轴承外圈故障模拟时域图

(b) 轴承外圈故障模拟频域图

Fig.11 Fault simulation time domain and frequency domain of bearing outer race

(a) 轴承外圈故障实验时域图

(b) 轴承外圈故障实验频域图

Fig.12 Fault experimental time domain and frequency domain of bearing outer race

通过对建立的模型进行求解计算，将得到的模拟数据与实验数据进行对比，可以看出误差值都在5%之内。对实验数据、模拟数据分别与表2理论计算的数据分别进行对比，误差都在容许的范围内(5%)。综上所述，模型数据与实验数据的基本吻合说明所建立的二自由度模型是可行的，能用于滚动轴承局部缺陷动力学响应分析。

6.2 弹流润滑作用下滚动体滑动对滚动轴承系统局部缺陷振动响应的影响

图13(a)和(b)为弹流润滑及滑动作用下滚动轴承系统内、外圈局部缺陷滑动时域、频域图。将图13(a)与图13(b)分别与图9(b)与图11(b)进行对比可以看出主频没有变化，但是加入滑动后幅值增大了。内圈高频阶段的幅值增大，外圈相对内圈在一倍频处提前出现幅值的增大。幅值的大小反映了振动能量的大小，幅值增大说明轴承运转时内部激励增加。内部激励力会加速轴承的损坏，对缺陷的演变起促进作用。

6.3 弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励不同状态下的振动响应

为研究弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励不同工况下对轴承运转振动响应的影响，分别对同一条件下不同转速、载荷进行研究。轴转速分别为1 750 r/min、1 772 r/min、1 800 r/min，径向载荷为450 N、500 N。

图14(a)、(b)为轴转速1 772 r/min、载荷为450 N，内圈、外圈缺陷大小为0.177 8 mm时弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励内圈、外圈频谱图。将图14(a)和(b) 分别与图13(a)、(b)进行比较，其内圈、外圈特征频率幅值都增大，边频带上幅值也有增加。图15(a)和(b)为1 800 r/min、载荷为450 N，局部缺陷大小为时弹流润滑及滑动作用下滚动轴承系统局部缺陷位移激励内圈与外圈频谱图。将图15(a)和(b)与图14(a)和(b)进行比较，发现内圈幅值明显的增大，尤其在边频带处幅值增加更加明显。外圈在二倍频及三倍频处幅值增大，外圈幅值的增加在高倍频上比较明显。通过对图13、图14和图15的对比，可以看出在同一缺陷大小工况下，轴转速越高，特征频率处幅值也越大。当转速增加到1 800 r/min时，内圈边频带上幅值的增加特别明显，这是转速增加时，会产生一定的离心力，而本文所建立的二自由度模型中没有考虑离心力的作用。

(a) 1 750 r/min轴承内圈滑动频谱图

(b) 1 750 r/min轴承外圈滑动频谱图

Fig.13 The bearing sliding frequency spectrum of inner and out race in 1 750 r/min

(a) 1 772 r/min内圈频域

图14 1 772 r/min载荷450 N缺陷大小为0.177 8 mm内、外圈频域图

Fig.14 The load 450 N frequency spectrum of defect size under 0.177 8 mm of inner and out race in 1 772 r/min

(a) 1 800 r/min内圈频谱图

(b) 1 800 r/min外圈频谱图

图15 1 800 r/min载荷450 N缺陷大小为0.177 8 mm内、外圈频域图

Fig.15 The load 450 N frequency spectrum of defect size under 0.177 8 mm of inner and out race in 1 800 r/min

图16(a)和(b)、图17(a)和(b)、图18(a)和(b)为径向载荷500 N时，缺陷大小为0.177 8mm、轴转速分别为1 750 r/min、1 772 r/min、1 800 r/min的频谱图。对图16与图13进行对比分析，可以看出增大载荷内圈特征频率幅值下降，边频带幅值增加。可能导致内圈特征频率幅值减小的原因是由于载荷的增加，缺陷处接触变形、间隙减小导致幅值的下降，边频带部分幅值增大。对于外圈，载荷增大时外圈特征频率幅值增大，同时特征频率附近幅值也增大。分别对图16 (a)、(b)、图17(a)、(b)和图18(a)、(b)内圈、外圈特征频率幅值进行对比，可以明显的看出随着转速的增加，振动响应幅值也随之增大；载荷变化时外圈特征频率幅值变化大，而内圈在速度较低时在特征频率上幅值变化比较大，当转速增加时边频带的幅值增加明显快于特征值频率幅值的增加。

综上所述，主轴转速增加时内圈、外圈特征频率幅值都会发生变化，内圈在边频带、高频段都出现幅值的增大；而外圈基本直接反应在故障特征频率的增加。可以看出随着轴转速、载荷的增大，都会引起滚动轴承系统局部缺陷位移内部激励的增大而使振动响应幅值增加，破坏了轴承系统正常运行。

6.4 弹流润滑及滑动作用下滚动轴承系统局部缺陷增大时的振动响应

图19(a)和(b)为滚动轴承系统局部缺陷位移激励二自由度模型在1 750 r/min、载荷为500 N、缺陷尺寸为0.355 6 mm时的频谱图。将图19(a)、(b)分别与图16(a)、(b)进行对比，从图(a)对比可以看到内圈缺陷增大时，其主频上幅值变化不大，而边频带上幅值变化比较大；从图(b)中对比可以看出外圈缺陷增大时，其2倍频幅值增大。文献[18]对干接触及润滑条件下对外滚道相同缺陷位置缺陷大小为0.2 mm、0.4 mm、0.6 mm做了讨论并得出结论随着缺陷的增大外滚道幅值明显增大。将本文结果与文献[18]得到的结果进行对比分析，外滚道幅值增大的趋势是一致的。

(a) 1 750 r/min内圈500 N频域图

(b) 1 750 r/min外圈500 N频域图

图16 1 750 r/min载荷500 N缺陷大小为0.177 8 mm内、外圈频域

Fig.16 The load 500 N frequency spectrum of defect size under 0.177 8 mm of inner and out race in 1 750 r/min

(a) 1 772 r/min内圈500 N频域图

(b) 1 772 r/min外圈500 N频域图

图17 1 772 r/min载荷500 N缺陷大小为0.177 8 mm内、外圈频域

Fig.17 The load 500 N frequency spectrum of defect size under 0.177 8 mm of inner and out race in 1 772 r/min

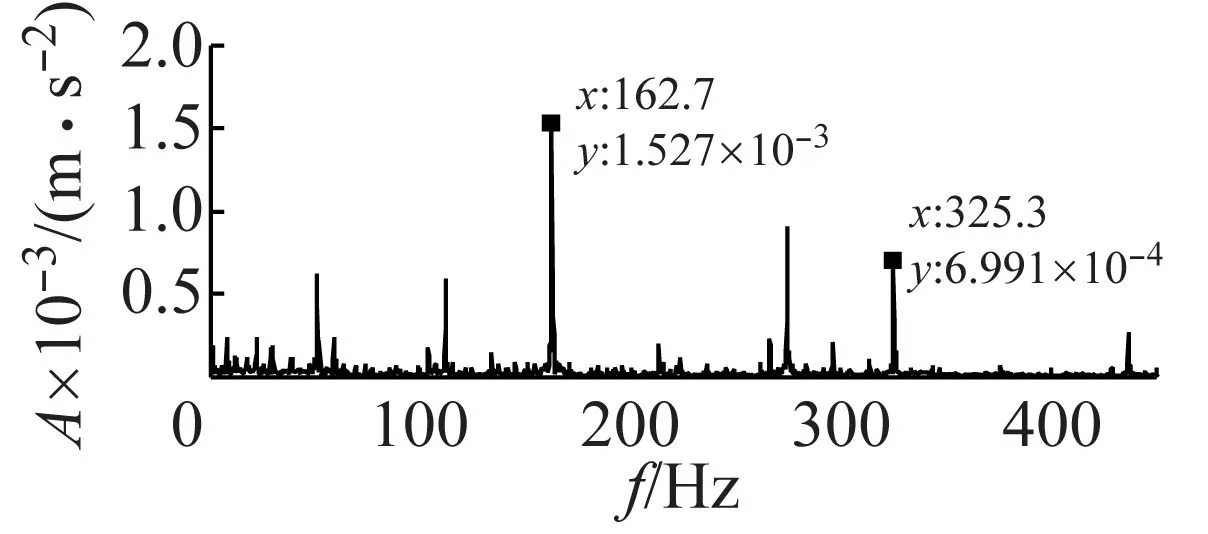
(a) 1 800 r/min内圈500 N频域图

(b) 1 800 r/min外圈500 N频域图

图18 1 800 r/min载荷500 N缺陷大小为0.177 8 mm内、外圈频域

Fig.18 The load 500 N frequency spectrum of defect size under 0.177 8 mm of inner and out race in 1 800 r/min

(a) 1 750 r/min内圈缺陷为0.355 6 mm频谱图

(b) 1 750 r/min外圈缺陷为0.355 6 mm频谱图

Fig.19 The spectrum of defect size under 0.355 6 mm of inner and out race in 1 750 r/min

7 结 论

(1) 考虑轴承座、油膜的影响因素对所建模型的数据、试验数据与理论数据对比分析，三者的数据基本吻合证明了所建模型的正确性。

(2) 轴承存在局部缺陷时对振动有很大的影响。局部缺陷引起冲击成分，使频域中出现冲击波形破坏轴承正常的运转。当滚动体与滚道出现滑动时，冲击成分增大，加剧了轴承的损坏。

(3) 轴承局部缺陷系统在载荷、转速和缺陷大小增加后会分别使轴承频域中冲击增大，反映出轴承内部激励力增加进而使轴承损坏更加快速，缩短轴承正常运转的周期。

[1] JONES A B. Ball motion and sliding friction in ball bearings[J]. Journal of Basic Engineering,1959,81(3):1-12.

[2] GUPTA P K, PAUL B. Advanced dynamics of rolling elements[J]. Journal of Applied Mechanics, 1986, 53(3):76-99.

[3] LIAO N T, LIN J F(Member STLE). Rolling-sliding analysis in ball bearing considering thermal effect[J]. Tribology Transactions, 2006, 49(1):1-16.

[4] KULKARNI P G, SAHASRABUDHE A D. A dynamic model of ball bearing for simulating localized defects on outer race using cubic hermite spline[J]. Journal of Mechanical Science and Technology, 2014,28(9): 3433-3442.

[5] PATIL M S, MATHEW J, RAJENDRAKUMAR P K, et al. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing[J]. International Journal of Mechanical Sciences, 2010, 52(9):1193-1201.

[6] PATEL V N, PANDEY R K, TANDON N. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races[J]. Journal of Tribology, 2010, 132(4):041101-(1-10).

[7] SHAO Y, LIU J, YE J. A new method to model a localized surface defect in a cylindrical roller-bearing dynamic simulation[J]. Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, 2013, 228(2):140-159.

[8] PETERSEN D, HOWARD C, SAWALHI N, et al. Analysis of bearing stiffness variations, contact forces and vibrations in radially loaded double row rolling element bearings with raceway defects[J]. Mechanical Systems and Signal Processing, 2015,50(51):139-160.

[9] 刘静,邵毅敏,秦晓猛，等. 基于非理想Hertz线接触特性的圆柱滚子轴承局部故障动力学建模[J].机械工程学报，2014，50(1):91-97.

LIU Jing, SHAO Yimin, QIN Xiaomeng,et al. Dynamic modeling on localized defect of cylindrical roller bearing based on non-hertz line contact characteristics[J]. Jourmal of Mechanical Engineering, 2014,50(1):91-97.

[10] 曹宏瑞，何正嘉，訾艳阳.高速滚动轴承力学特性建模与损伤机理分析[J].振动与冲击，2012,31(19):134-140.

CAO Hongrui, HE Zhengjia, ZI Yanyang. Modeling of a high-speed rolling bearing and its damage mechanism analysis[J]. Journal of Vibration and Shock, 2012,31(19): 134-140.

[11] WIJNANT Y H, WENSING J A, NIJEN G C. The influence of lubrication on the dynamic behaviour of ball bearings[J]. Journal of Sound & Vibration, 1999, 222(4):579-596.

[12] WIEGERT B, HETZLER H, SEEMANN W. A simplified elastohydrodynamic contact model capturing the nonlinear vibration behaviour[J]. Tribology International, 2013, 59(2):79-89.

[13] LIAO N T, LIN L F. Ball bearing skidding under radial and axial loads[J]. Mechanism and Machine Theory, 2002, 37(1): 91-113.

[14] 张亚洲，石林锁.滚动轴承局部故障数学模型的建立与应用[J].振动与冲击，2010,29(4):73-76.

ZHANG Yazhou,SHI Linsuo. Establishment and application of mathematical models for rolling element bearing with localized faults[J]. Journal of Vibration and Shock, 2010, 29(4):73-76.

[15] BASTAMI A R, MBA D. A new model for estimating vibrations generated in the defective rolling element bearings[J]. Journal of Vibration & Acoustics, 2011, 133(4):783-789.

[16] SAWALHI N, RANDALL R B. Simulating gear and bearing interactions in the presence of faults: Part I. The combined gear bearing dynamic model and the simulation of localised bearing faults[J]. Mechanical Systems and Signal Processing, 2008, 22(22):1924-1951.

[17] PATIL M S, MATHEW J, RAJENDRAKUMAR P K, et al. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing[J]. International Journal of Mechanical Sciences, 2010, 52(9):1193-1201.

[18] 剡昌锋, 苑浩, 王鑫,等. 点接触弹流润滑条件下的深沟球轴承表面局部缺陷动力学建模[J]. 振动与冲击, 2016, 35(14):61-70.

YAN Changfeng, YUAN Hao, WANG Xin, et al. Dynamics modeling on localized defect of deep groove ball bearing under point contact elasto-hydrodynamic lubrication condition[J]. Journal of Vibration and Shock, 2016, 35(14):61-70.

[19] 康建雄, 剡昌锋, 苑浩，等. 考虑弹流润滑和滚动体滑动的滚动轴承局部缺陷动力学建模[J]. 振动与冲击, 2016, 35(增刊1):178-181.

KANG Jianxiong, YAN Changfeng, YUAN Hao, et al. Dynamics modeling of local defect of rolling ball bearings under elasto-hydrodynamic lubrication and slipping conditions[J]. Journal of Vibration and Shock, 2016, 35(Sup 1):178-181.

[20] DOWSON D, HIGGINSON G R. The effect of material properties on the lubrication of elastic rollers[J]. ARCHIVE Journal of Mechanical Enginnering Science, 1960, 2(2):188-194.

[21] HAMROCK B J, DOWSON D. Isothermal elastohydrody-namic lubrication of point contacts: Part III—Fully flooded results[J]. Journal of Tribology, 1976, 99(1):264-275.

[22] 赵联春. 球轴承振动的研究[D]. 杭州：浙江大学, 2003.

[23] HAGIU G D, GAFITANU M D. Dynamic characteristics of high speed angular contact ball bearings[J]. Wear, 1997, 211(1):22-29.

[24] WALFORD T L H, STONE B J, WALFORD T L H. The sources of damping in rolling element bearings under oscillating conditions[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 1983, 197(4):225-232.