盈利因子与投资因子具有定价能力吗?
——来自中国股市的实证
2018-03-28张信东李建莹
■张信东,李建莹
一、引言
股票价格由哪些因素决定?Fama&French(1993)通过选取美国三大证券交易所(NYSE、AMEX、NASDAQ)1963年至1990年上市公司股票数据进行实证分析,研究发现包括市场因子、规模因子和价值因子的三因子模型可以更好地解释股票未来回报。这一研究奠定了资本资产定价实证领域的基石,将传统金融的发展提升到一个新高度。毋庸置疑,Fama-French三因子模型得到了学术界的高度认可,并且被广泛地用来指导实践。随着资本资产定价模型的不断完善和发展,Fama-French将反映公司基本面信息的盈利和投资纳入定价模型,构建了包括市场因子、规模因子、价值因子、盈利因子和投资因子的五因子模型。五因子模型系统性地将盈利和投资提炼为定价因子,且通过实证证实了盈利因子和投资因子的定价地位,这一发现将资产收益和风险关系的认识提升到一个新视角,进一步完善了定价模型。那么在中国股市中五因子模型是否具有适用性即盈利因子和投资因子是否可以定价,学界少有涉足。因此,本文将以1999年至2017年沪深两市A股数据为样本对这一问题进行探究,检验盈利能力和投资水平是否可以作为定价因子更好地预测中国股市的股票价格。
在已有研究中,大多数学者对三因子模型在中国股市的适用性进行了探讨,以检验市场、规模和价值因子在我国股市的定价能力。例如:刘维奇等(2010)研究发现我国股市股权分置改革前后三因子模型均有效;田利辉(2014)分析了三因子模型在中美两国股市表现的差异,研究发现我国股市系统性风险突出且存在市值规模效应,但是账面市值比效应并不显著;李倩和梅婷(2015)研究了三因子模型在股价上涨和衰退时期的适用性,发现衰退时表现最好,账市比因素不显著。但是,关于五因子模型在中国股市适用性的研究尚少,仅赵胜民等(2016)和高春亭等(2016)两篇文章对五因子模型进行了研究,且研究结论不同。具体地讲,赵胜民等研究表明我国股市市值效应和价值效应显著,盈利因子和投资因子无益于解释股票组合的回报率。与美国股市不同,价值因子在我国股市中不是冗余因子,三因子模型更适合我国股票市场定价;高春亭等研究发现规模、账市比、盈利和投资四个因素的显著性依次减弱,五因子模型在表现上优于三因子模型。
仅此一端就告诉我们,关于因子模型定价能力在我国的实证探究结论各执一词,进一步研究盈利因子和投资因子的定价能力具有非凡的意义。与已有文献相比,本文研究的创新点在于进一步拓宽了样本时间区间,且采用正交化投资因子的五因子模型进行实证分析,这是以往研究未曾涉足的。研究结论也和已有研究结论不同,本文研究发现我国股市中存在显著的规模效应、账面市值比效应和盈利效应,投资因子无益于解释股价。这一结论与我国新常态发展特征下表现出的机制不健全、市场投机现象较为严重等特征不谋而合。本文研究有助于借鉴和汲取国际先进的研究思想,丰富发展我国金融市场相关学术研究的广度和深度,充实国内金融理论。
二、文献综述
长期以来,资本资产定价的均衡模型备受学术界的关注。且经过五十多年的发展已经涌现了大量的资产定价模型,包括CAPM模型、APT模型、ICAPM模型、流动性定价模型和Fama-French类因子模型等。其中,最具关键意义的是Fama-French类因子模型,这些模型旨在构建一些能够解释股票未来回报的因子,以发现资产价格的决定因素。
Sharpe(1964)基于 Markowitz的均值方差理论提出资本资产定价模型即CAPM模型,随后Lintner(1965)和Mossin(1966)也提出该模型。该模型的基本思想是资产的收益取决于资产所携带的风险,反映了市场均衡状态下单个证券期望收益率与市场组合收益率之间的定价关系。但因CAPM模型以完美的假设前提为基础,复杂的现实很难完全满足而受到挑战;Ross(1976)放宽了传统资产定价模型的严格假设条件,提出一个多因子模型的套利定价理论(APT)。套利定价理论认为,套利行为是市场均衡形成的决定性因素,且根据无套利原则得出风险资产均衡收益与多个因素之间存在线性关系。
APT理论虽提供了一个从多因素对资产收益进行线性定价的思想,但因未给出具体的因素也饱受质疑;CAPM模型研究的是静态单个时期下投资者的均值方差最优选择,考虑到现实世界处于变化的动态过程,Merton(1973)提出了跨时期资本资产定价模型(ICAPM)。ICAPM模型反映的是在多期环境下,经济状态和投资机会发生变化,投资者会动态调整最优资产组合而形成的均衡价格。Jr(1974)也提出了一个基于离散时间下跨期资本资产定价模型,该模型研究了消费者对商品未来价格不确定和利率期限结构的反应,以及由此产生的投资组合选择和股票均衡定价。
随着CAPM模型的推广和应用,很多学者发现市场对股票收益缺乏解释,与此同时公司规模和账面市值比等非传统因素对股票未来回报有较强的解释力。例如:Banz(1981)研究发现1964年后的美国股市中小规模公司的股票拥有更高的收益;Stattman(1980)研究表明账面市值比和美国股票收益之间存在正向相关的关系。在前人各项研究的基础上,Fama&French(1993)通过按上市公司某些特征排序构建投资组合模拟因子的方法探究股票收益由哪些因素决定,研究发现由市场因素、规模因素和账市比因素构成的三因子模型可以更好地对股票未来回报进行预测,三因子模型由此成为资产定价模型的代表。
不少学者也发现,反映公司基本信息的盈利和投资因素与股票价格之间存在着必然的联系。例如:Haugen&Baker(1996)以1979年至1993年为周期,运用线性因子模型探究预测股票收益的变量,研究发现投资对全球主要国家(美国、法国、德国、日本、英国)股票市场预期收益产生决定性作用;Sloan(1996)研究表明公司盈利对股票价格存在显著影响。近期的研究如Watanabe et al.(2013)的研究表明在国际股票市场中,资产增长率高的公司随后会经历更低的股票收益,且这一现象在发达资本市场更显著;Hou et al.(2015)将净资产收益率ROE作为衡量公司盈利能力的指标,实证分析发现投资水平和盈利能力影响股票未来回报。且提出了投资机理和ROE机理即预期收益和投资具有负相关关系,和盈利具有正相关关系。直到2015年Fama&French首次将盈利因素和投资因素纳入到定价模型,进一步完善了资产定价模型且将其提升到了一个新的高度。
那么,五因子模型在我国股票市场中表现如何?和三因子相比新加入的盈利因子和投资因子是否增强了模型的解释力呢?在中国市场上哪些因子更适用?这些问题的探讨对我国股票定价理论的发展意义重大。基于此,本文使用沪深两市股票数据进行分析,以Fama-French类因子模型为基础,采用GRS统计检验和时间序列回归法对盈利因子和投资因子在中国股市的定价能力进行检验。发现有意义的结论:在中国股票市场,盈利因子可以预测股票未来回报,盈利能力高的公司股票预期收益高;而投资能力和股票未来回报之间未呈现显著的变化规律,且投资因子是冗余因子。这与我国资本市场有效性不足和投资者更关注眼前利益这一实际相吻合。由此对这一领域的研究进行补充,同时为我国股票定价提供实证证据。
三、研究设计
(一)研究数据
本文中股票月收益数据和财务数据均来源于Wind数据库。样本选取1999年至2017年沪深A股所有上市公司股票月收益数据及财务报表中资产总计、营业利润和所有者权益合计数据。数据筛选标准为依次剔除:(1)金融类公司的股票;(2)上市时间不足一年的股票;(3)B/M为负的股票;(4)实施ST和*ST的股票;(5)数据缺失或错误的股票。其中,无风险利率(RF)使用三个月定期存款利率转换的月利率衡量;市场收益(RM)以样本股流通市值为权重的股票月收益计算;上市公司的规模(Size)采用t-1年末的股票收盘价和流通股总股数的乘积表示;账面市值比(B/M)由t-1年末公司股东的权益和总市值之比得到;盈利能力(OP)是上一年度财务报告中营业利润和所有者权益合计之比;投资能力(INV)表示t-1期总资产的增长和t-2期总资产之比。
(二)模型描述
本文以Fama-French三因子模型和五因子模型为基础,实证检验盈利因子和投资因子在中国股市的定价能力。三因子模型反映了市值加权市场超额收益、公司规模和账市比这三个因素可以较好地解释投资组合的超额收益。三因子模型的具体形式为:
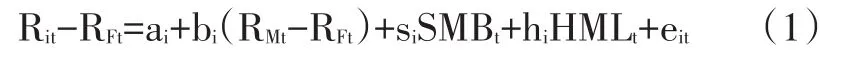
在式(1)中,Rit表示证券或投资组合i在t时期的收益率;RFt表示无风险利率;RMt表示市值加权市场投资组合的收益率;SMBt表示t时期小规模投资组合与大规模投资组合的收益率之差;HMLt表示t时期高账面市值比的价值型公司投资组合与低账面市值比的成长型公司投资组合的收益率之差;ai表示截距项,其含义是组合超额收益中三因子模型无法解释的部分;bi、si、hi为因子载荷;eit为随机扰动项。
五因子模型在三因子模型的基础上添加了盈利因子和投资因子,其具体形式为:
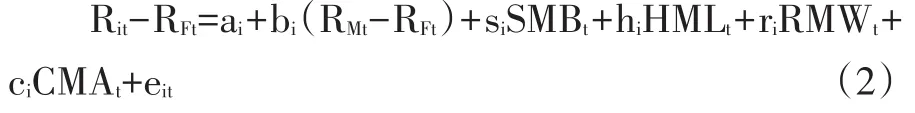
在式(2)中,RMWt表示t时期盈利高的公司投资组合与盈利低的公司投资组合的收益率之差;CMAt表示t时期投资保守的公司投资组合和投资激进的公司投资组合的收益率之差;系数和其余变量的定义和式(1)相同。若以上五个因子能够完全解释股票预期收益,则对于所有证券或投资组合i来说截距项ai为零。
(三)投资组合和因子定义
本文于每年四月末构建投资组合。具体构建方法为:每年四月末,将股票按流通市值从小到大分成五组,按照B/M、OP和INV从小到大将股票独立分为五等份。由此交叉形成5×5投资组合,然后计算各投资组合的月平均超额收益。5×5投资组合月平均超额收益作为式(1)和式(2)左边的部分Rit-RFt,用于三因子和五因子模型的时间序列回归分析。
本文因子的构建参照Fama&French(2015)构建因子的方法,对因子采用三种不同的分类方法(2×3构建法、2×2构建法和2×2×2×2构建法)进行构建。其中,2×3构建法是先将规模按照从小到大排序分为两组分别记为小规模组(S)和大规模组(B),将B/M(OP或INV)从小到大排序,按照30%、40%和30%的比例将其独立分为三组,依次得到账市比高(H)、中(N)和低(L)三组,盈利能力强(R)、中(N)和弱(R)三组以及投资保守(C)、中等(N)和投资激进(A)三组。然后将规模和账市比(盈利或投资)交叉构建2×3投资组合;2×2构建法和2×3构建法相似,不同之处在于2×2构建法是将B/M(OP或INV)按照中位数分为两组;2×2×2×2构建法则采用联合控制各变量的方法,将规模、账面市值比、盈利和投资按照中位数各自分为两组,形成2×2×2×2投资组合。
(四)因子汇总统计
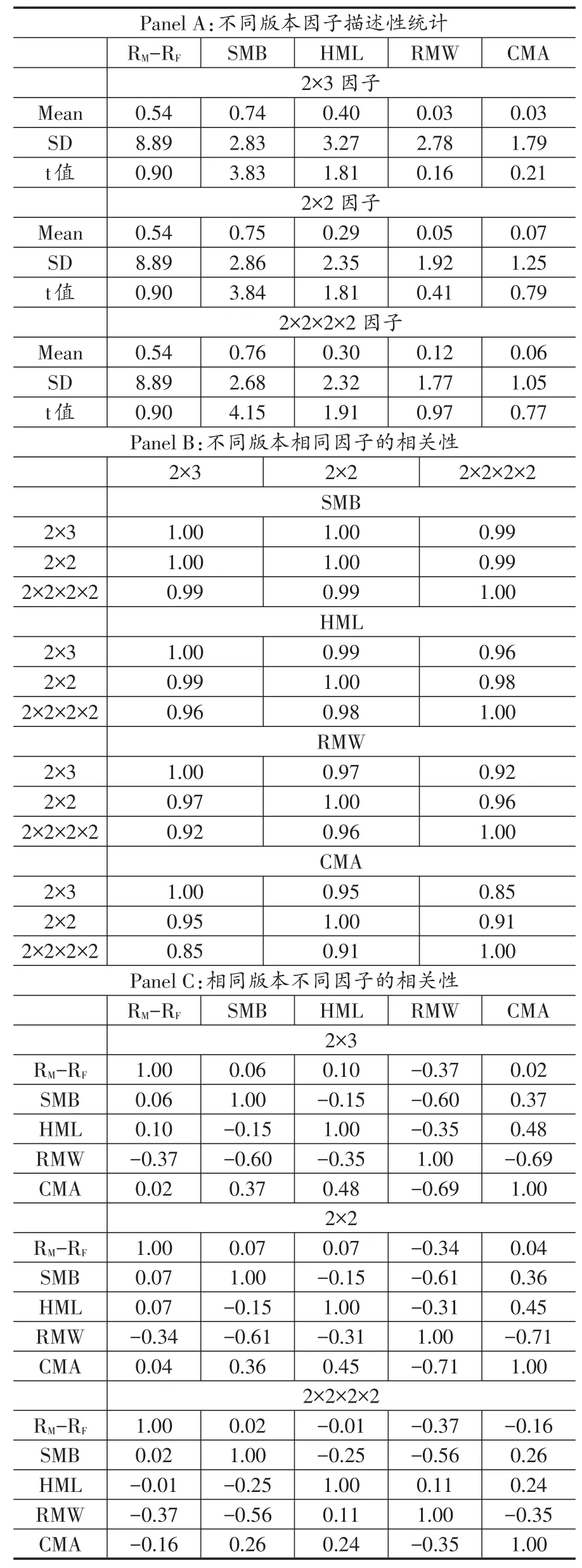
表1 不同版本因子特征
表1描述了不同构建方法下因子的特征,其中面板A呈现了不同版本因子的描述性统计,面板B呈现了不同版本相同因子的相关性,面板C呈现了不同版本不同因子的相关性。由面板A和面板B可以看出,三个版本规模因子SMB的均值(0.74、0.75、0.76)和标准差(2.83、2.86、2.68)相近,且不同版本的SMB高度相关。究其原因在于规模分组始终采用中位数作为断点,并且三个版本的SMB包括了所有的股票。对于HML、RMW和CMA这三个因子而言,更多依赖于其如何构建。对比2×3和2×2构建法下三个因子的特征,不难发现当B/M、OP和INV使用中位数进行分组产生了更低的标准差。这是因为2×3分组并未包括B/M、OP和INV中40%的股票,而2×2分组包括了所有的股票。2×3和2×2分组构建的每个因子均控制了规模和其中一个变量,而2×2×2×2构建法下控制了所有变量,因此联合控制产生了最小的标准差(2.32、1.77、1.05)。
对于盈利因子RMW和投资因子CMA来说,2×2×2×2版本与其他两个版本因子的相关性均较低。2×2×2×2版本和2×2版本相比较RMW有较低标准差,但是联合控制下的RMW产生了更高的均值(0.12)。投资因子CMA的标准差从2×2版本的1.25下降到2×2×2×2版本的1.05,且均值从0.07下降到0.06。从面板C可以看出,与FF(2015)的发现(投资因子和盈利因子的相关性很低)不同,本文发现投资因子和盈利因子的相关性很高且为负相关。
四、实证结果和分析
(一)盈利和投资因子的定价能力检验
为了检验盈利因子和投资因子是否可以提高股票定价模型的解释力,本文首先采用Gibbons et al.(1989)提出的GRS检验对各模型拟合不同投资组合平均收益的效果进行检验。GRS检验以5×5组合月度超额收益回归的截距项是否同时为零作为原假设,具体检验结果如表2所示。限于篇幅,本文仅呈现Size-B/M投资组合中不同构建法因子的GRS检验结果①限于篇幅,本文未能给出Size-OP和Size-INV组合的GRS检验结果,留存备索。。
从表2可以看出,在Size-B/M投资组合中,包含盈利因子和投资因子的五因子模型在各项指标上的表现均比三因子模型好,且在不同版本因子中五因子模型均稳健好于三因子模型。具体地讲,加入盈利因子和投资因子的五因子模型的GRS(p)值均大于三因子模型(0.26和0.02、0.27和0.02、0.20和0.01);五因子模型的A|ai|值也小于三因子模型(0.15和0.18、0.15和0.18、0.15和0.21);A|ai|/A|rˉl|值的测量上包含盈利因子和投资因子的五因子模型表现更好(0.38和0.48、0.39和0.48、0.39和0.54),这说明平均收益未被五因子模型解释的部分很少,盈利因子和投资因子的加入提高了模型定价能力。
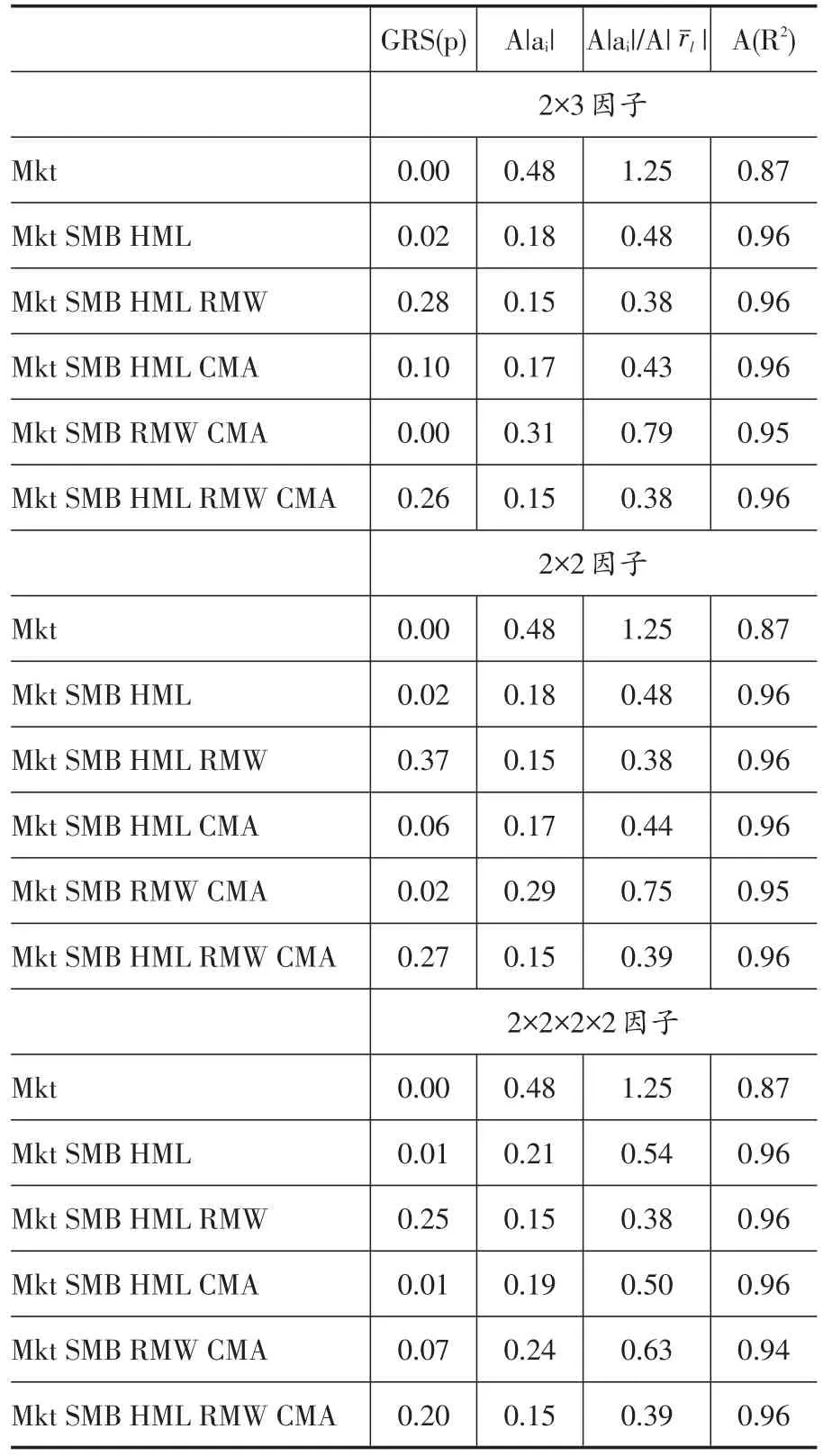
表2 Size-B/M组合的GRS检验
但是我们发现,不包括投资因子的四因子模型和五因子模型对平均收益的解释力不相上下。表2中包含盈利因子的四因子模型的GRS(p)值比五因子模型更大(0.28和0.26、0.37和0.27、0.25和0.20),这说明盈利因子可以更好地对股票进行定价,投资因子的加入无关紧要甚至降低模型的解释力。这一现象在不同组合和不同因子构建法下均稳健。
为了进一步检验是否投资因子无益于解释股票收益,以此证实上述实证结果是否在统计意义上可行。本节借鉴Fama&French(2014)的冗余因子测试进行检验。该检验是对模型中一个因子与其余因子进行回归,若该因子被其余因子的暴露所捕捉,则该因子的加入对平均收益的解释没有意义。
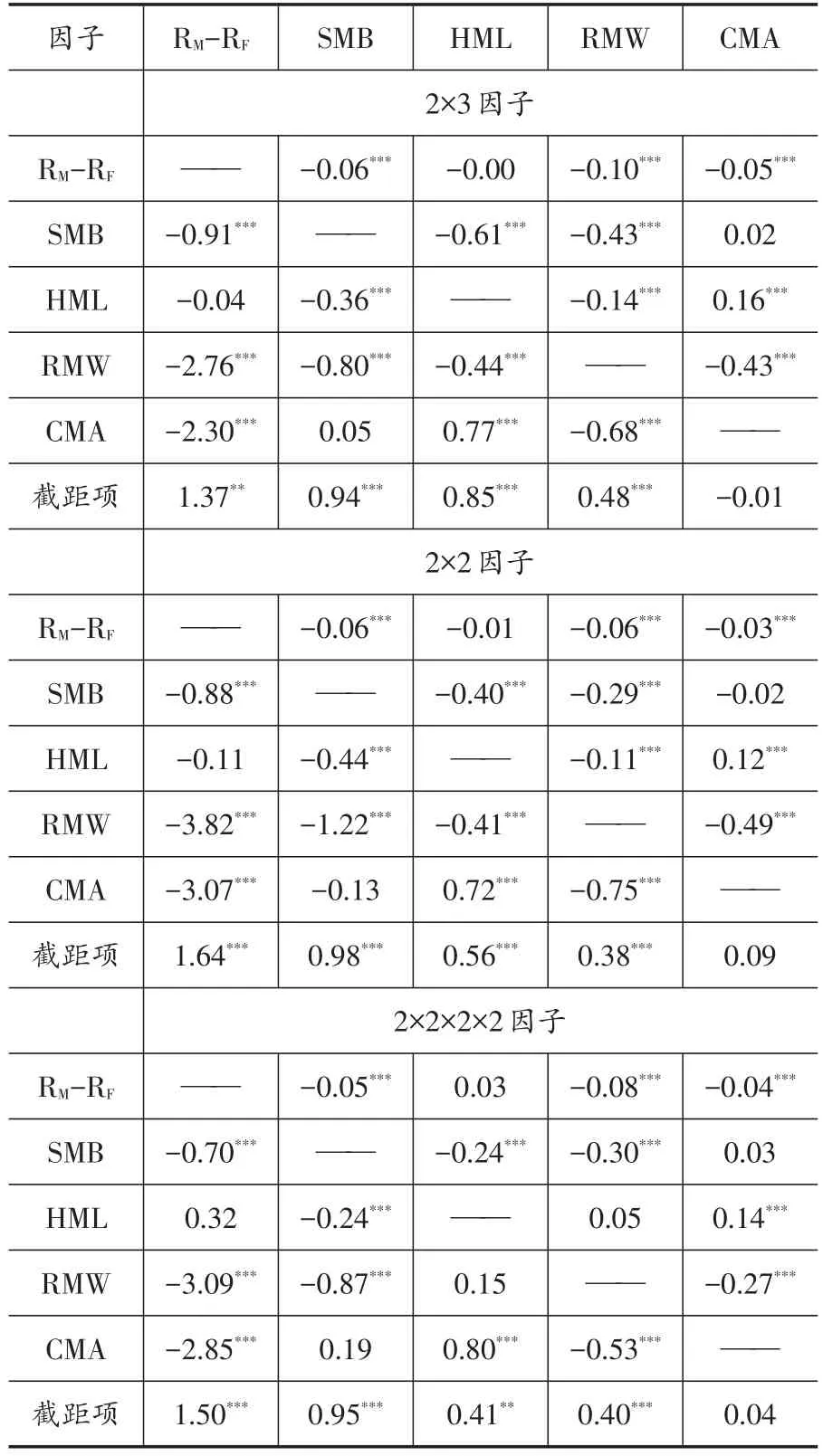
表3 五因子模型冗余因子检验
从表3数据分析发现,投资因子的截距项不显著异于零,且对于不同版本的投资因子都是冗余的(-0.01、0.09和0.04)。相比之下,在2×3因子构建法下,市场因子、规模因子、账市比因子和盈利因子截距项均显著异于零(1.37、0.94、0.85和0.48),且同样适用于2×2和2×2×2×2构建法下的因子。这里为了更好地研究投资因子的定价能力和避免回归时出现多重共线性,本文保留投资因子CMA并对其进行正交化处理,将正交化处理后的投资因子CMAO作为CMA的代理变量。得到新的五因子模型如(3)式所示,本文在之后的回归中将采用(3)式进行回归分析。
在Fama&French(2015)研究中价值因子被盈利因子和投资因子的暴露所捕捉,成为冗余因子。而在本文研究中,代表公司成长性的价值因子并非冗余因子,且有益于解释股票预期收益。究其原因,价值因子是账面价值和市场价值的直观体现,其中市场价值是投资者对市场未来的预测,间接反映了投资者对市场未来发展的态度。而我国股票市场投资者非理性投资、羊群现象严重,因此使得价值因子对股票收益的作用不容小觑,这一实证结果的发现具有理论层面的渊源关系。
(二)投资组合回归分析
为了更详细地洞察模型的表现,接下来我们对资产定价模型进行回归。在回归前,首先对组合收益的特征及变化规律进行描述性统计。5×5 Size-B/M、Size-OP和Size-INV投资组合每月平均超额收益具体变化特征如表4所示。
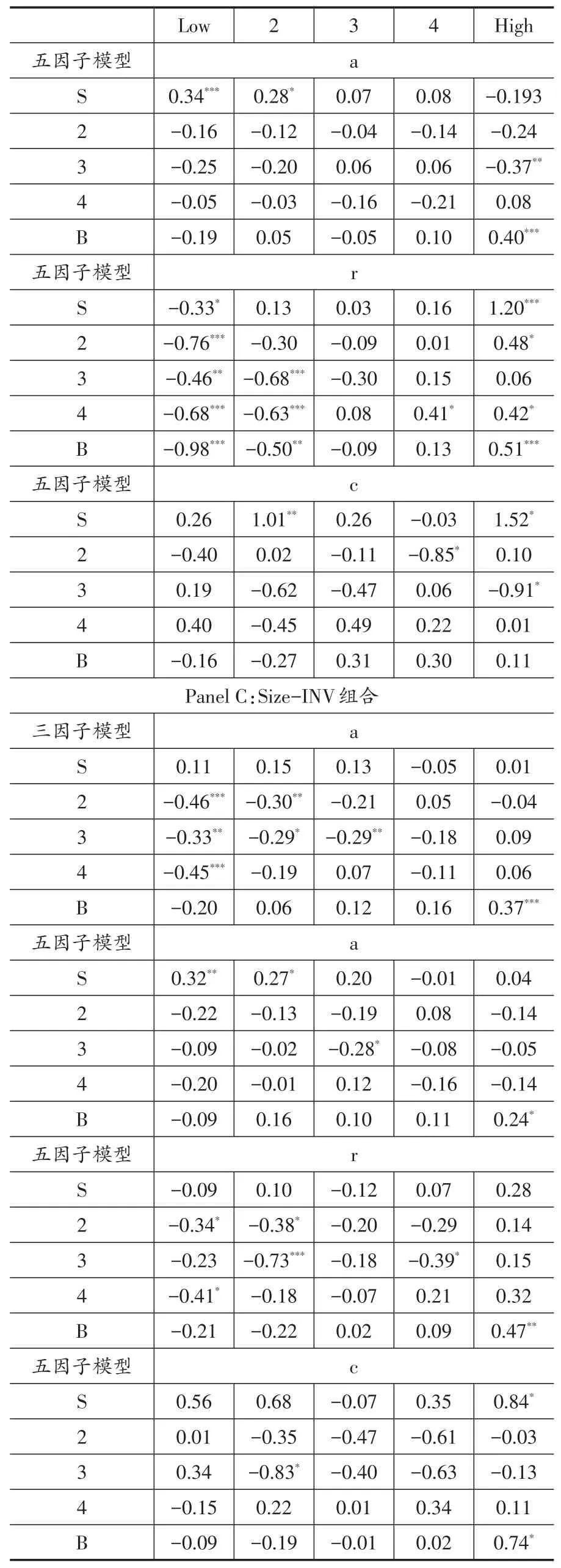
从表4可以看出,在面板A(25 Size-B/M)、面板B(25 Size-OP)和面板C(25 Size-INV)中,规模较小组的平均收益高于规模较高组的平均收益,个别组除外(例如:在面板A的最低账市比中,第三规模组上投资组合的平均收益0.73相比第二规模组的值0.72略大,但不明显)。且每个规模组投资组合平均超额收益的均值从小规模组到大规模组依次降低。这说明对于我国股票市场来说,存在显著的规模效应(小盘股效应),即小市值股票所获收益比大市值股票收益高。从面板A的数据可以看出,给定规模,股票收益基本服从随账市比升高而变高的规律,而且各列均值从左往右依次变高,这与美国市场上高账市比高收益结论相一致。从面板B的数据可以看出:规模最小组的收益随盈利能力的增强而变低,但在最高OP组出现反转;其余规模组收益基本随OP的升高而变高,但在第2、3规模组的最高OP列也出现翘尾现象。不过通过各列均值表现出来的特征表明股票收益随盈利能力的增强而变高,这与美国股市表现出来的特征相同,但是表现出翘尾现象。从面板C的数据可以看出,在第1、3、5规模组中,收益从左往右有变小趋势;但是在其余两列却相反。从各列均值来看,前三列呈现出股票收益和投资具有正相关关系,后两列却相反。以上分析可以发现,我国股市中规模效应、价值效应和盈利效应显著,且盈利效应存在翘尾现象,投资水平和收益之间没有明确的变化规律。

表4 5×5投资组合平均超额收益
为了更好地检验盈利因子和投资因子的定价能力,本文接下来将采用时间序列回归方法对三因子模型和包括盈利、投资的五因子模型进行回归分析。具体回归结果如表5所示。由于两模型回归的市场因子、规模因子和价值因子均显著且无很大差异,因此表5省略了其估计结果。
表5中面板A为规模和账市比组合的回归结果。不难发现,在规模和账市比组合中,三因子模型截距项在1%、5%、10%显著性水平上分别有1个、4个和2个显著异于零,而五因子模型在1%、5%显著性水平上分别有1个和2个截距项显著异于零。这说明在解释规模-账面市值比组合收益上,加入盈利因子和投资因子的五因子模型比三因子模型解释力更好。而盈利因子系数在5%和10%显著性水平上分别有1个和2个显著异于零,投资因子只有2个在5%水平上显著异于零,这说明盈利因子更具备定价能力。
表5中面板B为规模和营运利润组合的回归结果。可以得出:在该组合中,三因子模型截距项有9个显著异于零,其中在1%、5%水平上显著异于零的分别有6个和3个。五因子模型截距项有4个显著异于零,其中在1%、5%、10%显著性水平上分别有2个、1个和1个显著异于零。这说明在解释规模-盈利组合收益上,加入盈利因子和投资因子的五因子模型比三因子模型解释力更好。不难发现,盈利因子的系数有一半以上均显著异于零,且系数在盈利能力最低的组显著为负,依次变高至盈利最高组显著为正,这与表4中盈利能力和股票收益的变化特征相一致。这表明盈利因子有益于解释股票预期收益,盈利因子的加入增强了模型的解释力。而投资因子的系数只有4个显著异于零。进一步验证了投资因子在我国股市中缺乏定价能力。
表5中面板C为规模和投资组合的回归结果。从面板C可得出,三因子模型的截距项在1%、5%、10%显著性水平上分别有3个、3个、1个显著异于零。但在五因子模型中,仅有4个截距项显著异于零,其中有1个在5%水平上显著异于零,有3个在10%水平上显著异于零。这说明在解释规模-投资组合收益上,加入盈利因子和投资因子的五因子模型比三因子模型解释力更好。同样我们发现,盈利因子系数有6个显著异于零,而投资因子系数只有3个显著异于零。
通过本节实证分析我们发现,在我国股票市场中有显著的规模效应、价值效应和盈利效应,盈利效应特征表现出了翘尾现象。进一步的回归分析得出,在解释我国股票收益上Fama-French五因子模型比三因子模型更好,特别是盈利因子的加入增强了模型的解释力。与Fama&French(2015)的研究不同,我国股市中投资水平对于股票未来回报的解释力不足。这是因为中国股市发展时间短,资本市场尚不成熟,投资者更关注公司的盈利,对代表公司更深层面的价值(公司投资)的关注少。

表5 三因子模型和五因子模型回归结果
续表5
五、结论与启示
本文以1999年至2017年沪深A股所有上市公司股票月度收益数据为样本,运用构建投资组合计算因子法和时间序列回归法探究盈利因子和投资因子是否有益于解释股票未来的回报即我国股市中盈利因子和投资因子是否具有定价能力。通过实证检验得出主要结论如下:
第一,在2×3、2×2和2×2×2×2三种不同的因子构建法下,包含盈利因子和投资因子的五因子模型表现优于三因子模型。而且不包括投资因子的四因子模型和五因子模型的表现不相上下。进一步,本文通过冗余因子检验发现,在我国股票市场中投资因子CMA为冗余因子,且在三种不同版本的因子冗余测试中均稳健。
第二,在我国股市中,规模效应、账面市值比效应和盈利效应显著,投资效应特征未表现出明显的变化规律。具体地讲,规模效应和账市比效应特征和美国股市一样,其中规模效应表现出小规模组合拥有更高的股票收益特征,账面市值比效应表现出高账市比高收益的特征。盈利效应表现出的特征为盈利能力越强收益越高,但是存在翘尾现象。
第三,在Size-B/M、Size-OP和Size-INV投资组合回归中,三因子模型回归截距项显著异于零的个数均明显多于加入盈利因子和投资因子的五因子模型,且盈利因子系数显著异于零的个数较多。这说明盈利因子的加入增强了模型的解释力,投资因子无益于预测股票收益。
以上结论的得出与我国股票市场的发展程度和相关特征相一致。我国股市处于日益完善进程中,有以下几个主要特征:一是散户投资者占比大,机构投资者占比小,投机现象较严重,羊群效应、追涨杀跌等非理性投资行为致使市场效率低下;二是市场监管制度尚未健全,监管掣肘等现象严重,对股市有效管理能力较缺乏;三是信息不对称、信息失真现象较为严重,导致股票交易价格偏离其真实价值,部分投资者权益受损。致使投资因素不能有效发挥其定价作用。
进一步思考,虽然盈利和投资均反映了上市公司的基本面信息,但是两者仍存在本质区别。具体讲,盈利是公司创造价值的直观体现,是投资者真正关心的指标;相比之下,投资则具有风险,且投资带来的收益在当前无法计算,需要投资者对其进行预测。在市场机制不健全的情况下,投资者更关注眼前的获利,并不关注公司的发展前景。致使盈利因子对股票价格的解释力强。同时,投资者更关注价值型公司的信息,缺乏对成长型公司的关注。
本研究为我国股票定价相关领域提供了实证证据和文献支持,具有一定的理论意义。同时,本文也具有现实指导意义。具体体现在:(1)对于证券市场的投资者而言,在投资的过程中应避免羊群效应、追涨杀跌等非理性投资行为。应更加关注上市公司的潜在价值,可以通过上市公司定期的信息披露和重大事项公告等信息理性指导投资实践。(2)就上市公司而言,应该加大信息公开的力度,确保公开信息的准确性,为投资者投资决策提供更多的参考。(3)从监管者角度出发,应健全相关制度,对股市有效管理,在学习欧美成熟市场经验的同时也需结合中国特色,以确保中国股票市场健康发展。
[1]卜永祥.中国区域金融改革的探索与展望[J].金融与经济,2017,(09):4~14.
[2]高春亭,周孝华.公司盈利、投资与资产定价:基于中国股市的实证[J].管理工程学报,2016,30(4):25~33.
[3]李倩,梅婷.三因素模型方法探析及适用性再检验:基于上证A股的经验数据[J].管理世界,2015,(04):184~185.
[4]刘维奇,牛晋霞,张信东.股权分置改革与资本市场效率——基于三因子模型的实证检验[J].会计研究,2010,(3):65~72.
[5]田利辉,王冠英,张伟.三因素模型定价:中国与美国有何不同?[J].国际金融研究,2014,(7):37~45.
[6]赵胜民,闫红蕾,张凯.Fama-French五因子模型比三因子模型更胜一筹吗——来自中国A股市场的经验证据[J].南开经济研究,2016,(2):41~59.
[7]Banz RW.The relationship between return and marketvalue ofcommon stocks[J].Journalof Financial Economics,1981,9(1):3~18.
[8]Fama E F,French K R.A five-factor asset pricing model[J].Journal of Financial Economics,2015,116(1):1~22.
[9]Fama E F,French K R.Common risk factors in the returns on stocks and bonds[J].Journal of Financial Economics,1993,33(1):3~56.
[10]Fama E F,French K R.Dissecting Anomalies with a Five-Factor Model[J].Review of Financial Studies,2014,29(1):69~103.
[11]Gibbons M R,Ross S A,Shanken J.A Test of the Efficiency of a Given Portfolio[J].Econometrica,1989,57(5):1121~52.
[12]Haugen R A,Baker N L.Commonality in the determinants of expected stock returns[J].Journal of Financial Economics,1996,41(3):401~439.
[13]Hou K,Xue C,Zhang L.Digesting anomalies:An investment approach[J].The Review of Financial Studies,2015,28(3):650~705.
[14]Jr J B L.Stock prices,inflation,and the term structure of interest rates[J].Journal of Financial Economics,1974,1(2):131~170.
[15]Lintner J.The Valuation of Risk Assets and Selection of Risky Investments in Stock Portfolios and Capital Budgets[J].Review of Economics and Statistics,1965,47(1):13~37.
[16]Markowitz H.Porfolio Selection[J].Theory&Practice of Investment Management Asset Allocation Valuation Portfolio Construction&Strategies Second Edition,1952,7(1):77~91.
[17]Merton R C.An Intertemporal Capital Asset Pricing Model[J].Econometrica,1973,41(5):867~887.
[18]Mossin J.Equilibrium in a Capital Asset Market[J].Econometrics,1966,34(4):768~83.
[19]Ross S A.The arbitrage theory of asset pricing[J].J.econ.theory,1976.
[20]Sharpe W F.Capital Asset Prices:A Theory of Market Equilibrium under Conditions of Risk[J].Journal of Finance,1964,19(3):425~42.
[21]Sloan R G.Do Stock Prices Fully Reflect Information in Accruals and Cash Flows about Future Earnings?[J].SocialScience Electronic Publishing,1996,71(3):289~315.
[22]Stattman D.Book values and stock returns[J].The Chicago MBA:A Journal of Selected Papers,1980,4:25~45.
[23]WatanabeA,XuYetal..Theassetgrowtheffect:Insights from international equity markets[J].Journal of Financial Economics,2013,108(2):529~563.
