大型水平轴风力机塔影效应特性研究
2018-03-27胡丹梅张建平
胡丹梅, 潘 扬, 张建平
(上海电力学院 能源与机械工程学院, 上海 200090)
塔影效应是指由于塔架对流场的干涉,导致塔架附近叶片的工作特性发生变化。当水平轴风力机的叶片经过塔架附近时,空气作用于叶片上的气动载荷会随风速变化而变化,造成单个叶片的受力状况与其他叶片之间存在较大差异,这种差异对于风力机的正常运行是较为不利的。
塔影效应的研究起源于国外,其概念早在1968年便被提出,但当时的风力机技术处于起步阶段,作为非主要影响因素的塔影效应并未受到重视。进入21世纪后,随着风电产业的兴起,风电从业者开始认识到塔架对风力机的影响不可忽略,因此对塔影效应的研究逐渐增多。2001年,Wang等[1]建立了基于规定尾流涡模型和近尾流动力学模型的高分辨塔影效应模型,其计算结果在一定程度上与实际测量结果相符。Das等[2]为计算塔架造成的风力机周期波动,建立了有关塔影效应和风剪切效应的时域模型。对于3叶片风力机来说,一定时间内产生的振荡次数是旋转频率P的3倍,这种周期性波动称为3P效应。我国早期的研究着重于塔影效应对电力系统方面的影响。张玉良等[3]研究了塔影效应对风功率的影响,导出了下风向风力机的风功率计算式。李少林等[4]在设计动态风力机模拟器时涉及了对塔影效应的模拟,并计算出受塔影效应影响的等效风速,用以替代空间平均风速。由于叶片经过塔架时等效风速会发生脉动,可用等效风速计算出塔影效应引起的转矩脉动。张雪等[5]和董升等[6]均进行了基于等效风速法的风力机塔影效应和风剪切效应仿真研究,并得出了相似的结果。范忠瑶等[7]以东方汽轮机有限公司的2.5 MW上风向型DF90为模型,进行了塔影效应的数值模拟,研究表明塔影效应使单个叶片载荷波动20%~40%,风轮载荷波动6%~12%,且风轮的旋转作用导致塔前来流始终发生偏转,引起塔架两侧受力不均。
目前,国内外对于塔影效应的研究尚未成熟,特别是对兆瓦级大型风力机的数值模拟相对较少。笔者采用Fluent软件对美国可再生能源实验室(NREL)的5 MW风力机进行模拟,分析在不同来流风速下塔影效应的表现,为后续减弱塔影效应的研究提供参考。
1 风力机3D建模及网格划分
1.1 建立模型
选取NREL 5 MW风力机作为研究对象,风力机为3叶片上风向,叶轮直径为126 m,叶片长度为61.5 m[8]。将文献[8]中叶片17个截面处的弦长和翼型数据导入ProE软件中,通过连接翼型生成叶片模型。将轮毂简化为球体,机舱简化为长方体,将塔筒设为上底面直径为3.87 m、下底面直径为6 m的圆台,将包括叶片在内的各组件进行组装,得到整机模型。为了模拟出风力机运行时叶轮转动的工作状态,需将风力机的外部流场(计算域)分为2个部分,即将叶轮完全包围并随之旋转的圆盘状旋转域和旋转域外围不随叶轮旋转的静止域,如图1所示。旋转域半径为70 m,深度为8 m,关于旋转平面对称,旋转中心距地面高度为90 m;静止域入口距叶轮旋转平面为250 m,出口距叶轮旋转平面距离为1 000 m,宽为600 m,高为400 m,静止域为长方体。

图1 计算域模型
1.2 网格划分
采用ICEM-CFD网格划分软件对旋转域和静止域分别进行结构化网格划分。划分旋转域网格时,先划分出三分之一旋转域网格,再沿旋转轴进行周期性旋转,得到整个旋转域的计算网格,如图2所示。


图2 旋转域划分网格
对叶片外围流场进行O剖分,并单独划分流动边界层,如图3所示。由于风力机模型的叶轮直径达126 m,几何尺寸很大,为保证网格数量在可计算范围之内,沿叶片展向的网格节点数较少,导致边界层网格的长和宽较大。为防止网格长宽比过大,影响计算精度[9],采用壁面函数法处理边界层;为满足Y+要求[10],第1层网格高度为1.5 mm,网格增长比为1.1,共14层。

图3 不同叶高处的网格分布
Fig.3 Grid distribution at different blade heights

表1 不同网格数的计算结果比较
选取额定工况进行网格无关性验证,结果如表1所示。考虑到计算的准确性,选择网格数为626.75万,其中旋转域的网格数为346.37万,静止域的网格数为280.38万。
2 计算方法
2.1 控制方程
基于N-S方程进行数值模拟,考虑到湍流模型需与壁面函数法兼容,以及叶轮的旋转效应,选用带有湍流漩涡修正的RNGk-ε模型,离散格式为2阶迎风,利用Simple算法进行求解[11]。计算采用滑移网格法,旋转域设为以叶轮旋转轴为轴进行旋转,风力机部件视为刚性,不考虑流固耦合。
RNGk-ε模型的控制方程为[12]:

(1)

(2)
式中:ρ为空气密度;k为湍流脉动动能;ε为脉动耗散率;ρε为耗散项的密度;t为时间;xi为空间某一方向(i、j=1,2,3);ui为速度在某一方向上的分量(i、j=1,2,3);μeff为有效黏性系数;Gk为产生的湍流动能;Gb为浮力产生的湍流动能;YM为可压缩湍流中过渡扩散产生的波动;αk为湍流动能普朗特数的倒数;αε为湍流耗散率普朗特数的倒数;C1ε、C2ε和C3ε均为模型默认常数;Rε、Sk和Sε均为用户自定义项。
2.2 塔影效应
风力机叶轮的转矩为[13]:
(3)
(4)
式中:λ为叶尖速比;R为叶片旋转半径,m;ω为叶片旋转角速度,rad/s;Cp为功率系数;β为桨距角,(°);Tm为转矩,N·m;v为运动黏度,m2/s。
由式(3)可知,叶片桨距角一定时,叶轮转矩与叶轮上游处的风速有关。
3 模拟结果与分析
3.1 计算可信度验证
3.1.1 功率曲线验证
为验证数值模拟的准确性,选取25 m/s、20 m/s、15 m/s、11.4 m/s(额定风速)、9 m/s、7 m/s和5 m/s作为来流风速进行模拟。表2为各工况下的叶片桨距角[8]。如图4所示,模拟值和设计值的功率曲线在额定工况下符合情况较好,最大相对误差为4.6%,可认为模型和计算方法具有可信度。

表2 不同工况下的叶片桨距角

图4 风力机功率曲线
3.1.2 3P效应
设置11.4 m/s的均匀来流,旋转域的旋转角速度为12.1 rad/min,采用滑移网格法,设时间步长为0.027 548 2 s(对应旋转域旋转角度为2°),进行非定常计算。计算过程中对整个风力机叶轮和3个叶片分别进行转矩监测,待计算时间足够长,转矩趋于稳定后,记录叶轮旋转1周过程中的转矩,如图5所示。由图5可以看出,在叶轮旋转1周的过程中,相比于无塔筒,有塔筒时转矩出现3次大幅下降,且方位角相互间隔120°,符合3P效应。

图5 1个旋转周期内整个叶轮的转矩
3.2 模拟结果分析
3.2.1 塔影效应对叶片工作特性的影响
图6和图7分别为在11.4 m/s、9 m/s、7 m/s和5 m/s的来流风速下1根叶片在旋转1周过程中转矩和轴向推力的变化曲线,可较直观地反映塔筒对叶片工作特性的影响。叶片尖部垂直向上时方位角为0°,叶片在塔筒正前方时方位角为180°。
由图6(a)可知,在叶片的1个旋转周期内,转矩出现了1次谷值和2次峰值,谷值出现在方位角180°处(C点),2个峰值分别出现在方位角140°(B点)和210°处(A点),且210°处转矩大于140°处转矩。由图6可知,转矩的峰值和谷值出现的方位角不随来流风速的变化而改变。

(a) 来流风速为11.4 m/s,叶轮转速为12.1 rad/min
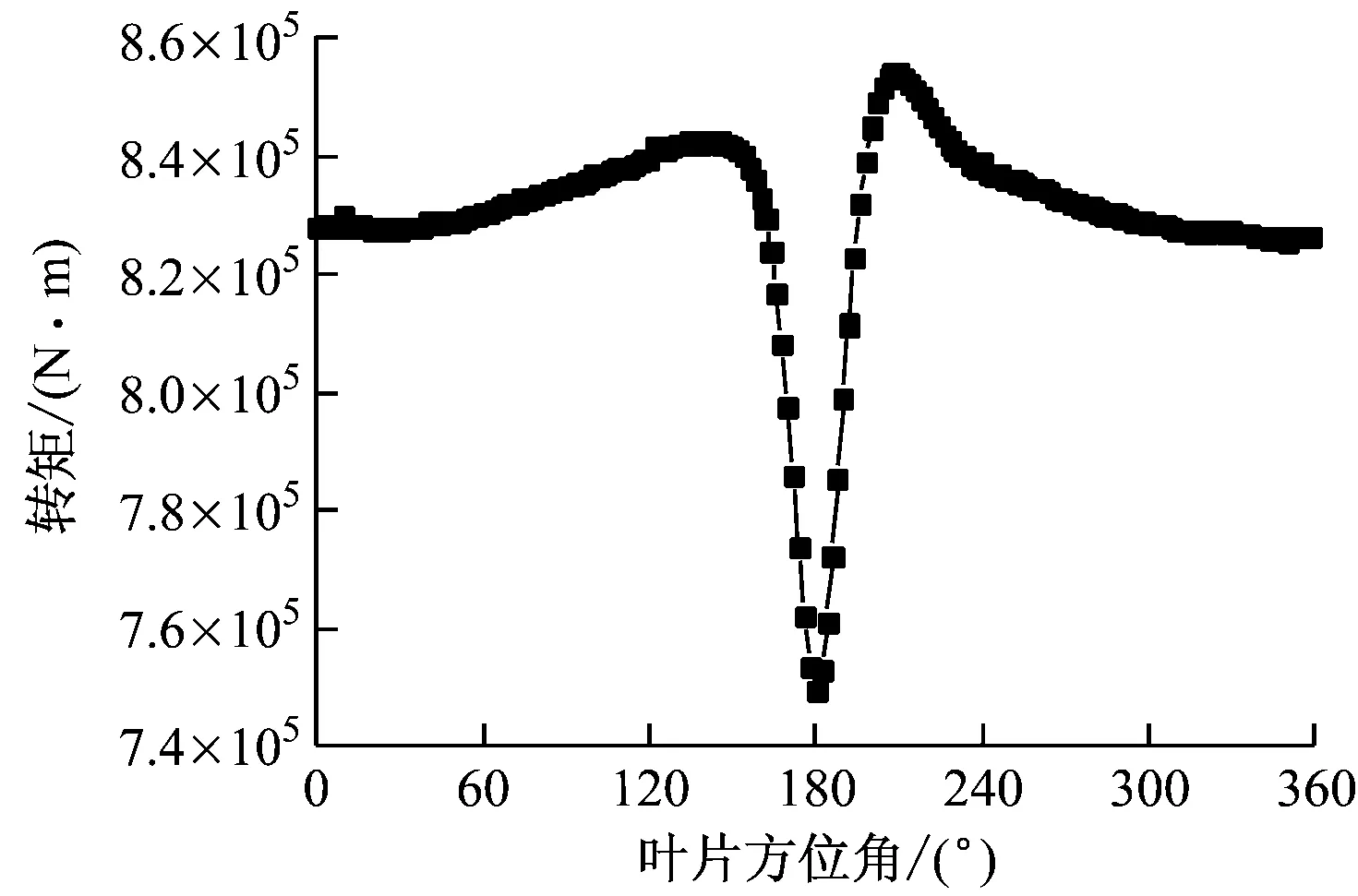
(b) 来流风速为9 m/s,叶轮转速为10.2 rad/min

(c) 来流风速为7 m/s,叶轮转速为8.3 rad/min

(d) 来流风速为5 m/s,叶轮转速为7.3 rad/min
将最大转矩和最小转矩的差值与叶片旋转1周的平均转矩的比值定义为转矩相对峰谷差,可表示为:
(5)
式中:TA为较大转矩峰值;TC为最小转矩;Tave为叶片旋转1周的平均转矩。
转矩相对峰谷差的大小代表输出转矩的相对波动幅度,其值越大,转矩的相对波动幅度越大。在4个来流风速下转矩相对峰谷差分别为12.85%、12.88%、13.25%和14.93%。
将转矩2个峰值之间的差值与叶片旋转1周的平均转矩的比值定义为转矩相对峰峰差,可表示为:
(6)
式中:TB为较小转矩峰值。
转矩相对峰峰差反映了叶片转矩波动规律的不对称性,其值越大,说明叶片在塔筒两侧时工况的差异越大。在4个来流风速下转矩相对峰峰差分别为1.36%、1.38%、1.83%和3.31%。综上,来流风速越小,塔影效应引起的转矩相对峰谷差越大,转矩相对峰峰差越大。
对比图6和图7可知,叶轮所受轴向推力的变化同样呈现峰-谷-峰规律。由图7(a)可知,峰值分别出现在方位角140°(B点)和210°处(A点),谷值出现在方位角180°处(C点)。如图7所示,峰谷值出现的方位角与图6中峰谷值的方位角一致,但140°处的峰值却高于210°处的峰值。与转矩相似,叶片所受轴向推力的峰值和谷值的方位角不随来流风速的变化而变化。因此可认为塔影效应对叶片的气动影响主要集中在叶片方位角140°~210°的时域内。
将最大轴向推力与最小轴向推力的差值与叶片旋转1周的平均轴向推力的比值定义为推力相对峰谷差,其表达式为:
(7)
式中:NB为较大轴向推力峰值;NC为最小轴向推力;Nave为叶片旋转1周的平均轴向推力。
推力相对峰谷差越大,说明叶片经过塔筒时受到的轴向推力变化越剧烈。在4个来流风速下轴向推力相对峰谷差分别为6.65%、6.16%、6.33%和5.68%。
将轴向推力2个峰值间的差值与叶片旋转1周的平均轴向推力的比值定义为推力相对峰峰差,其表达式为:
(8)
式中:NA为较大轴向推力峰值。
推力相对峰峰差越大,说明叶片在塔筒两侧时所受推力情况差异越大。在4个来流风速下推力相对峰峰差分别为1.22%、1.02%、0.62%和0.20%。
与转矩的变化特性相反,总体上叶片所受轴向推力的相对波动幅度随来流风速的减小而减小。

(a) 来流风速为11.4 m/s

(b) 来流风速为9 m/s
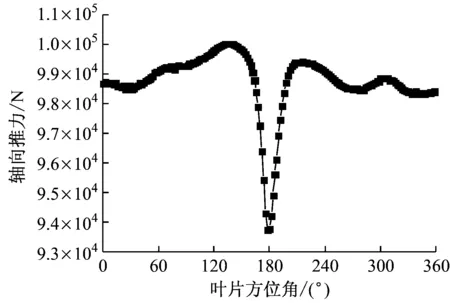
(c) 来流风速为7 m/s

(d) 来流风速为5 m/s
叶片转矩和轴向推力在方位角180°附近发生剧烈变化,说明叶片在塔筒附近时,气动特性受塔筒影响会发生较大改变。图8给出了塔影效应方程坐标,叶片的气动特性在塔筒两侧表现出一定程度的不对称性,这种不对称性在根据等效风速法计算出的结果中并未体现[4-6],而在同样使用数值模拟方法的结果中却有所体现[7,14]。
等效风速法[15]为:
v=vH+vtower
(9)
(10)
式中:v为等效风速;vH为轮毂高度处的风速;vtower为塔影效应下的风速;v0为空间平均风速;a为塔筒半径;y为叶片微元到塔筒中线的水平距离;x为叶轮旋转平面到塔筒中线的水平距离。
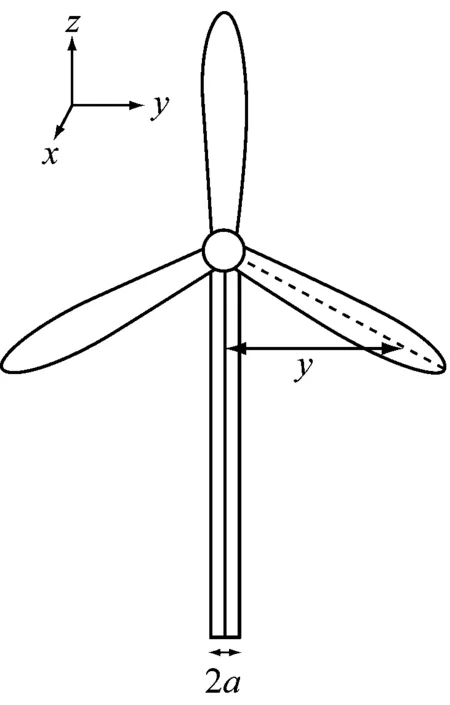
由式(10)可知,在等效风速法中,vtower在y方向上是关于塔筒对称的函数,且未考虑叶轮旋转造成的旋转效应,因此推测这种不对称性来源于旋转效应对风速的影响。为了进一步分析这种不对称性,图9给出了额定风速下叶片在方位角140°、150°、180°和210°处、水平高度为77.4 m平面的风速云图。
由图9可知,与普通的圆柱绕流相比,塔筒附近的速度分布沿顺时针方向有微小偏斜,偏斜方向与叶轮旋转方向一致,说明旋转效应造成了塔筒附近流场的不对称性;叶片尾部有一个低速区,反映了风经过叶片后动能的损失。按风速损失程度由大到小排序分别为图9(d)、图9(a)、图9(b)和图9(c),与转矩出现的峰-谷-峰变化规律相符,也解释了2个峰值在数值上的不对称性。

(a) 方位角140°处
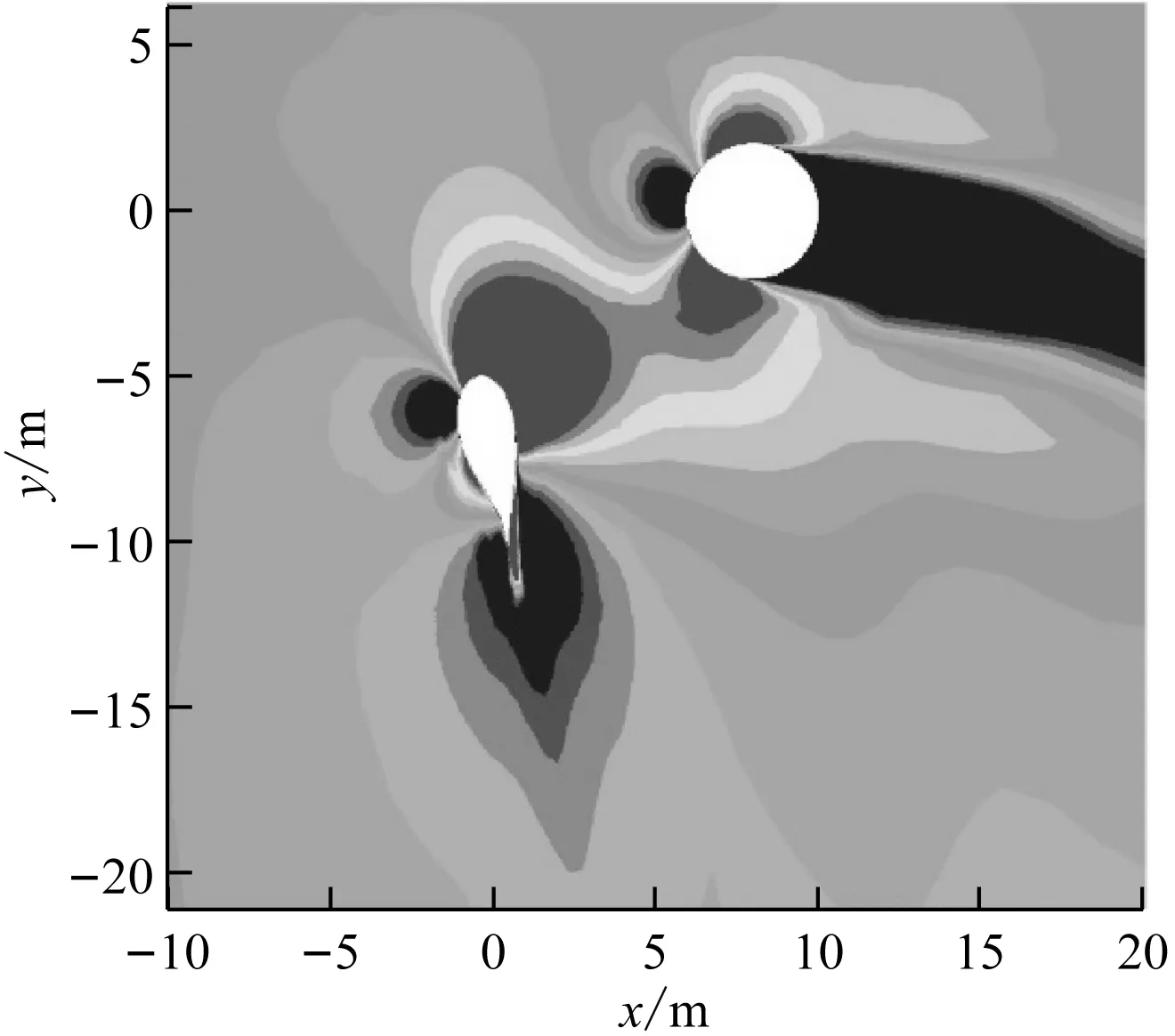
(b) 方位角150°处

(c) 方位角180°处

(d) 方位角210°处
为寻找能减弱塔影效应的有效对策,笔者在保持其他计算条件不变的情况下,将塔筒替换为桁架,并进行了模拟计算与分析。限于文章篇幅,仅列出分析结果,即与塔筒式风力机相比,桁架式风力机的叶轮和塔架所受气动载荷的波动程度均明显减小。
3.2.2 塔影效应下风力机流场及尾迹分析
计算出额定工况下风力机整机的周围流场,并与无塔筒时的流场进行对比。图10给出了叶片尖端指向地面时(对应叶片方位角180°)有、无塔筒情况下在叶片高度20%、40%、60%和80%处的流线及风速云图。由图10可知,与无塔筒相比,有塔筒时叶片周围近距离处流线的变化不大,塔筒对叶片的影响主要体现在速度场方面。在有塔筒的情况下,叶片周围的速度场受到明显“挤压”,叶片前缘处的高速区和尾缘处的低速区范围均小于无塔筒的情况。塔筒下游出现了不同程度的涡流,涡流大小随叶高的增大而减小,在20%和80%叶高处出现了涡流分离现象。对于风力机单机,塔影效应影响的关键区域在靠近叶根、弦长较大处,此处叶片近流场变化最为明显。
塔筒除了会干涉叶片周围的流场,也会对风力机下游的尾迹流场产生一定的影响。图11给出了在额定风速下20%、40%、60%和80%叶高处风力机尾迹流场的风速云图,发现塔筒对尾迹流场有明显干扰。无塔筒时,风力机尾流速度场基本关于叶轮中轴线呈对称分布。有塔筒时,除20%叶高处之外,其他3个截面处塔筒下游均出现了一个长度约为250 m(2D)的尾迹,且该尾迹在叶高较大处更为清晰。
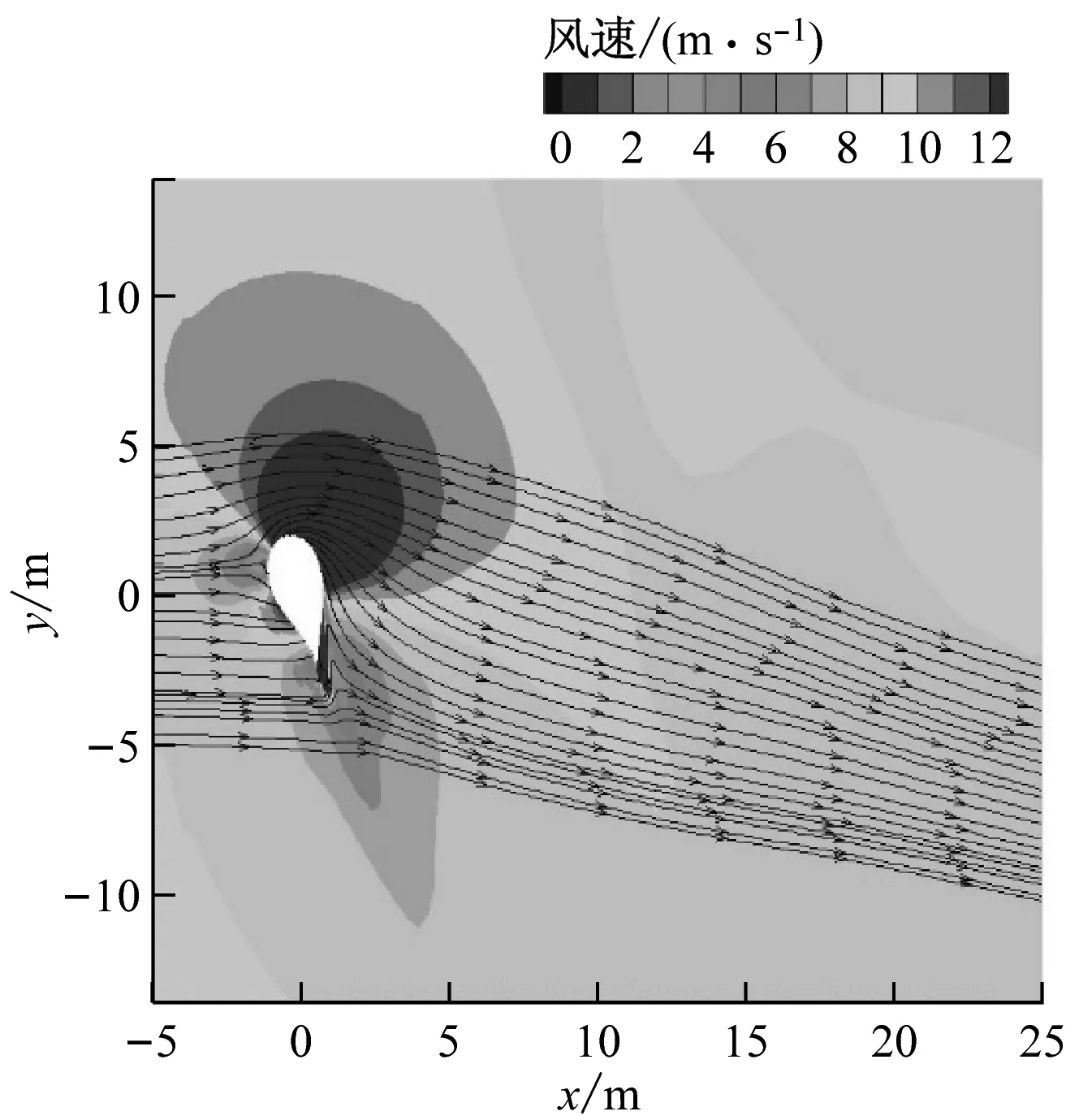
(a) 无塔筒、20%叶高处

(b) 有塔筒、20%叶高处

(c) 无塔筒、40%叶高处

(d) 有塔筒、40%叶高处

(e) 无塔筒、60%叶高处

(f) 有塔筒、60%叶高处
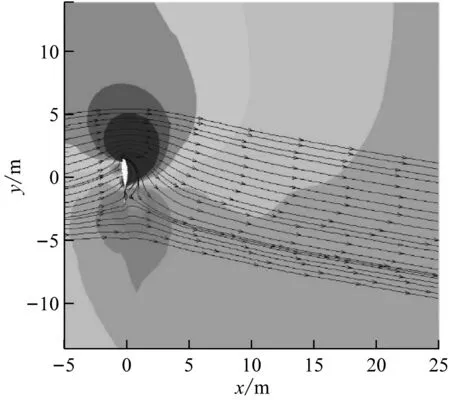
(g) 无塔筒、80%叶高处

(h) 有塔筒、80%叶高处
4 结 论
(1) 当来流风为均匀来流且风向一定时,不同来流风速下叶片在1个旋转周期内转矩和轴向推力的峰值、谷值出现在相同的叶片方位角, 140°~210°方位角是塔影效应的主要影响时域。当来流风速减小时,在叶片扫掠过塔筒的过程中,其转矩的相对波动幅度会减小,叶片所受轴向推力的相对波动幅度会增大。
(2) 在大型风力机的运行过程中,叶轮的旋转效应对塔筒引起的风力机工况变化特性有较明显的影响。其主要表现为叶片在靠近、远离塔筒的过程中,叶片转矩和轴向推力的变化规律具有不对称性,因此在大型风力机塔影效应的研究中有必要考虑旋转效应。
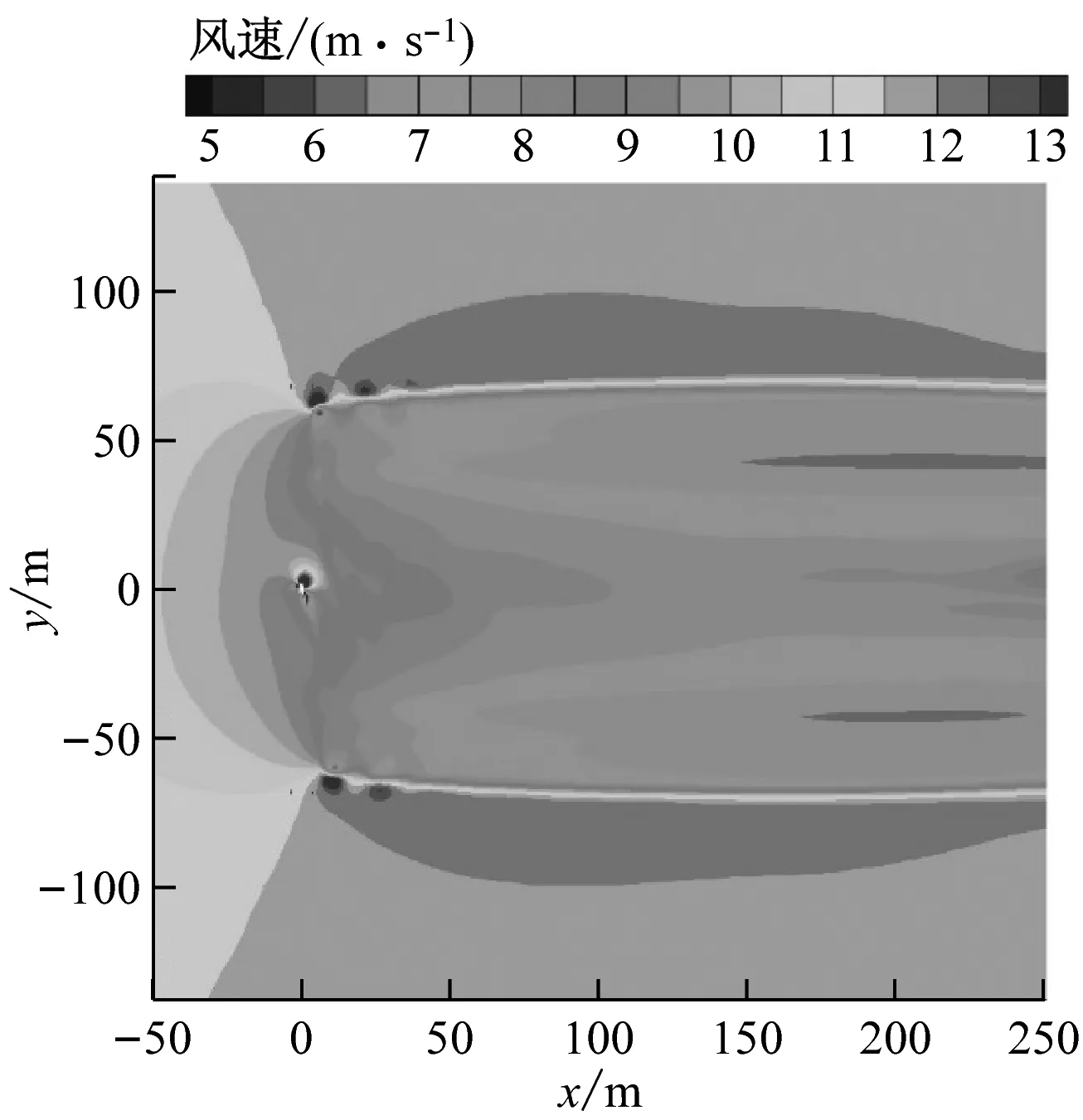
(a) 无塔筒、20%叶高处
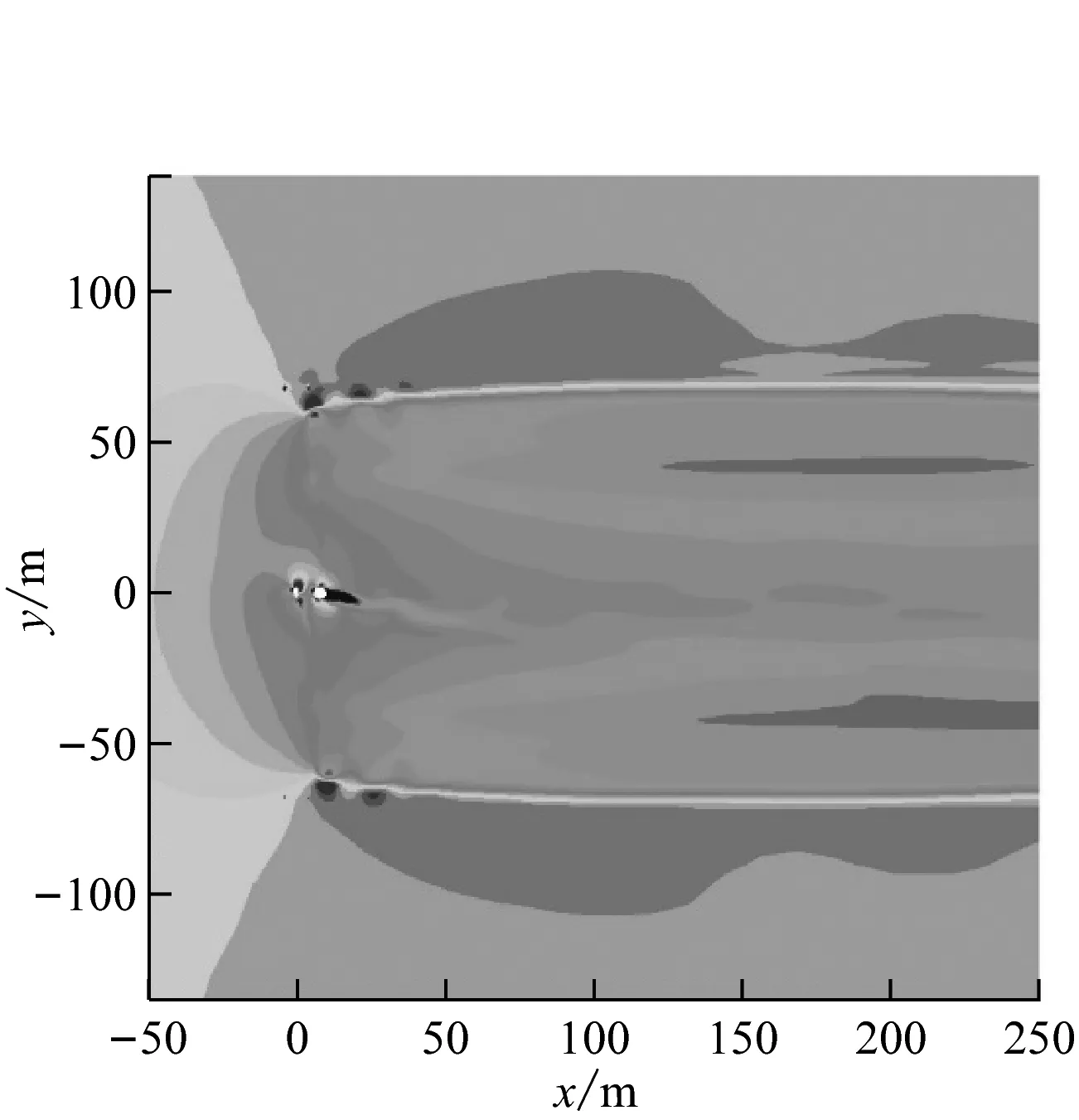
(b) 有塔筒、20%叶高处

(c) 无塔筒、40%叶高处
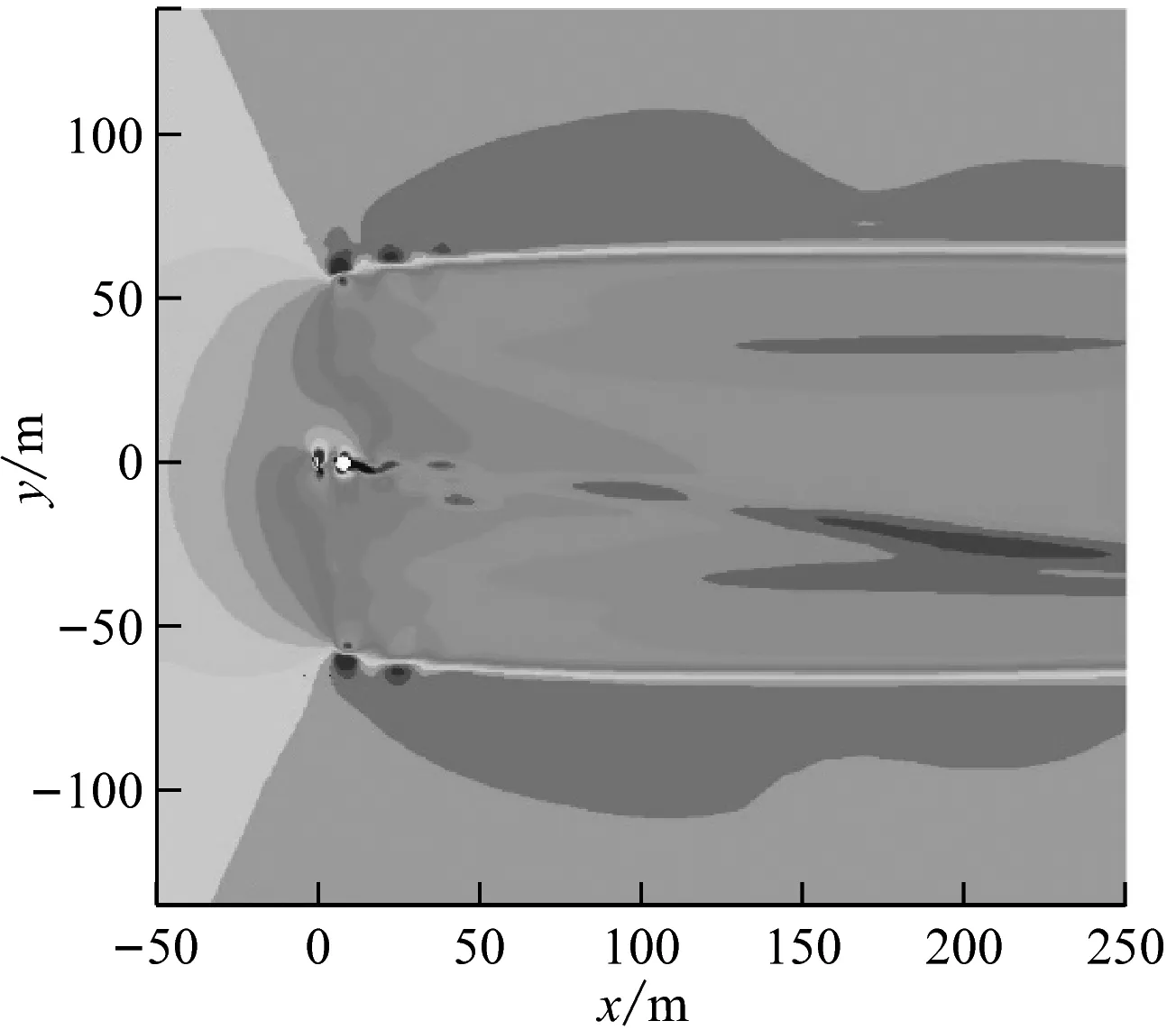
(d) 有塔筒、40%叶高处
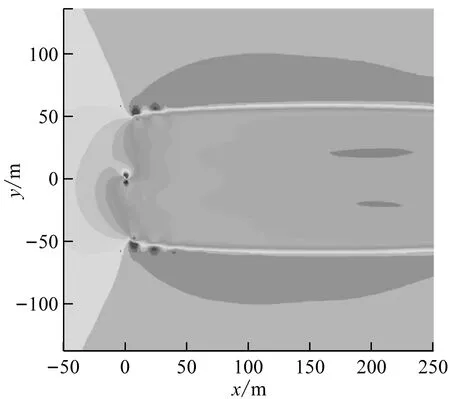
(e) 无塔筒、60%叶高处

(f) 有塔筒、60%叶高处

(g) 无塔筒、80%叶高处
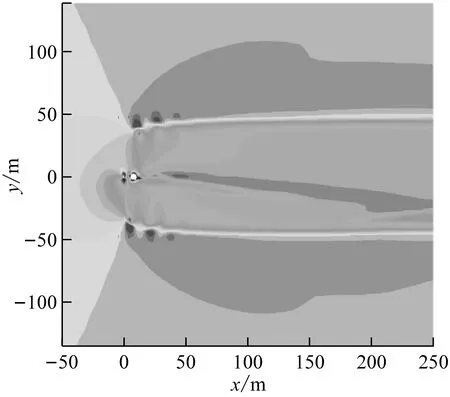
(h) 有塔筒、80%叶高处
(3) 塔筒对风力机流场的速度分布有显著影响。对于叶片附近流场,叶高越小处塔筒造成的影响越大,因此靠近叶根的部分是塔影效应影响风力机单机的关键区域;对于远尾迹流场,叶高越大处塔筒造成的尾迹越明显,塔筒尾迹长度约为叶轮直径的2倍。
[1] WANG Tongguang, COTON F N. A high resolution tower shadow model for downwind wind turbines[J].JournalofWindEngineeringandIndustrialAerodynamics, 2001, 89(1): 873-892.
[2] DAS S, KARNIK N, SANTOSO S. Time-domain modeling of tower shadow and wind shear in wind turbines[J].ISRNRenewableEnergy, 2011, 2011: 1-11.
[3] 张玉良, 李仁年, 巫发明. 下风向风力机的塔影效应研究[J].山东建筑大学学报, 2008, 23(3): 243-246.
ZHANG Yuliang, LI Rennian, WU Faming. The research of tower shade effect of down wind turbine[J].JournalofShandongJianzhuUniversity, 2008, 23(3): 243-246.
[4] 李少林, 张兴, 杨淑英, 等. 风力机动态模拟器的仿真研究[J].太阳能学报, 2010, 31(10): 1366-1372.
LI Shaolin, ZHANG Xing, YANG Shuying, et al. Simulation research of dynamic wind turbine simulator[J].ActaEnergiaeSolarisSinica, 2010, 31(10): 1366-1372.
[5] 张雪, 王维庆, 王海云, 等. 考虑风切和塔影效应的风力机风速模型[J].电测与仪表, 2015, 52(8): 56-60.
ZHANG Xue, WANG Weiqing, WANG Haiyun, et al. Model of wind speed considered wind shear and tower shadow effect on wind turbine[J].ElectricalMeasurement&Instrumentation, 2015, 52(8): 56-60.
[6] 董升, 周彪, 韩肖清. 基于剪切和塔影效应的风力机转矩脉动模型仿真研究[J].山西电力, 2016(1): 1-5.
DONG Sheng, ZHOU Biao, HAN Xiaoqing. Simulation of wind turbine torque pulsation model based on shear and tower shadow effect[J].ShanxiElectricPower, 2016(1): 1-5.
[7] 范忠瑶, 康顺, 赵萍. 上风向风力机塔影效应的数值模拟研究[J].工程热物理学报, 2012, 33(10): 1707-1710.
FAN Zhongyao, KANG Shun, ZHAO Ping. Numerical simulations of upwind wind turbine tower shadow effects[J].JournalofEngineeringThermophysics, 2012, 33(10): 1707-1710.
[8] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Springfield, USA: National Renewable Energy Laboratory, 2009.
[9] 漆文邦, 郑超. 基于单元不同长宽比网格划分的有限元误差分析研究[J].中国农村水利水电, 2010(2): 108-110, 113.
QI Wenbang, ZHENG Chao. A study of sensitivity to mesh distortion of isoparameter elements[J].ChinaRuralWaterandHydropower, 2010(2): 108-110, 113.
[10] 汪志成, 纪李文, 周书民, 等. 壁面参数对垂直轴风力发电机流体仿真的效果分析[J].现代制造工程, 2015(12): 43-46.
WANG Zhicheng, JI Liwen, ZHOU Shumin, et al. The analysis of numerical simulation performance for the vertical axis wind turbine on wall-parameter[J].ModernManufacturingEngineering, 2015(12): 43-46.
[11] 李少华, 匡青峰, 吴殿文, 等. 1.2 MW风力机整机流场的数值模拟[J].动力工程学报, 2011, 31(7): 551-556.
LI Shaohua, KUANG Qingfeng, WU Dianwen, et al. Numerical simulation on flow field of a 1.2 MW wind turbine[J].JournalofChineseSocietyofPowerEngineering, 2011, 31(7): 551-556.
[12] 任年鑫, 欧进萍. 大型海上风力机尾迹区域风场分析[J].计算力学学报, 2012, 29(3): 327-332.
REN Nianxin, OU Jinping. Numerical analysis for the wake zone of large offshore wind turbine[J].ChineseJournalofComputationalMechanics, 2012, 29(3): 327-332.
[13] 张弘鲲, 孟祥星. 塔影效应引起的风电机组输出功率波动问题[J].东北电力技术, 2011, 32(4): 33-35.
ZHANG Hongkun, MENG Xiangxing. On output power fluctuation of wind generators caused by tower shadow effect[J].NortheastElectricPowerTechnology, 2011, 32(4): 33-35.
[14] 田仁斌, 李学敏, 何成明, 等. 上风型水平轴风力机塔架干涉的数值模拟[J].工程热物理学报, 2014, 35(12): 2417-2420.
TIAN Renbin, LI Xuemin, HE Chengming, et al. Numerical simulation of upwind-type horizontal axis wind turbine blade-tower interaction[J].JournalofEngineeringThermophysics, 2014, 35(12): 2417-2420.
[15] DOLAN D S L, LEHN P W. Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow[J].IEEETransactionsonEnergyConversion, 2006, 21(3): 717-724.
