基于灰箱模型的中速磨煤机故障诊断方法

孙栓柱， 江叶峰， 董 顺， 周 挺， 代家元， 李益国

(1． 江苏方天电力技术有限公司， 南京 211102； 2． 江苏省电力公司， 南京 210024；3． 东南大学 能源与环境学院， 南京 210096)

磨煤机是燃煤电站制粉系统的核心设备，其运行状况会影响整个发电机组的安全性和经济性。磨煤机出力、出口风粉混合物温度、出口压力和煤粉细度等参数直接影响锅炉的燃烧，进而影响运行效率[1]。磨煤机运行一旦出现异常，一方面会影响运行效率，另一方面会造成设备故障，引起机组降负荷甚至停机。有效的故障诊断方法可以让操作人员及时了解磨煤机的运行状况并采取相应措施，避免突发性故障的发生，从而提高其运行的安全性，创造良好的经济效益。

磨煤机的经济性和安全性受一些常见故障的影响，如堵煤、断煤、煤粉自燃和辊子、磨盘及煤粉分离器叶片等碾磨组件的磨损等[2]。目前，磨煤机故障主要由经验丰富的操作人员来判断。由于控制中心接收到的信息量很大，缺乏知识和经验的操作人员往往不能正确地对数据进行分析。为了降低人员操作的复杂性，确保较高的可靠性，有必要开展磨煤机故障诊断技术的研究。目前，国内外学者进行了大量研究，可大致分为基于数学模型的故障诊断方法和基于人工智能的故障诊断方法2类。

在基于数学模型的故障诊断方法中，首先需要通过复杂的机理分析，建立数学模型作为被检测系统的先验数据源[3]，然后根据系统参数测量值和数学模型预测值之间的差值计算残差，并通过设定残差的阈值来判断故障是否发生。Fan等[4]利用简化的能量平衡方程建立了一种通用的磨煤机模型。该模型仅考虑了磨煤机各输入量对出口温度的影响，可以利用能量流动的异常判断故障的发生。Odgaard等[5]根据Rees等的模型，提出了基于检测的故障观测法和基于磨煤机简化能量平衡模型的燃煤含水量估计方法。Guo等[6]开发了一种磨煤机状态监测技术，其基于Wei等[7]开发的六段磨煤机模型，并通过模型参数是否有异常波动来监控磨煤机的运行状态。

上述单纯基于数学模型或单纯基于人工智能的故障诊断方法存在建模过程复杂或在样本不足的空间泛化能力弱等问题。笔者对中速磨煤机采用数学模型与人工智能混合的建模方法，基于小波变换原理，利用变换后的残差曲线提出了一种基于斜率阈值的早期故障检测方法，最后利用随机森林原理设计了故障类型分类器，能够根据不同参数残差信号的特征来区分故障类型。

1 基于遗传算法的中速磨煤机灰箱建模

1.1 模型基本假设

模型基本假设如下：(1) 忽略碾磨中煤的细度变化，磨煤机内煤的状态可分为原煤和煤粉2种；(2) 磨煤机中煤的研磨和输送过程互不影响；(3) 一次风是理想气体且比定压热容是常数；(4) 忽略磨煤机一次风和煤粉泄露；(5) 忽略磨煤机与外部环境的热交换。

1.2 机理模型建立

基于质量守恒的基本原则，首先建立磨煤机内部简化质量平衡模型，式(1)、式(2)为原煤和煤粉质量平衡微分方程：

(1)

(2)

式中：mc、mpf分别为磨煤机内部的原煤和煤粉质量，kg；qm,c、qm,pf分别为磨煤机入口原煤和出口煤粉的质量流量，kg/s；K10为待定的模型参数。

出口煤粉由一次风从磨煤机中携带出来，出口煤粉质量流量受一次风携带能力和磨煤机内存煤量的影响，故与一次风产生的压差和磨煤机内存煤量成正比：

qm,pf=K11Δpampf

(3)

式中：Δpa为一次风产生的压差，Pa；K11为待定的模型参数。

一次风压差与磨煤机入口一次风温度和质量流量的关系为：

(4)

式中：tin为磨煤机入口一次风温度，℃；qm,air为磨煤机入口一次风质量流量，kg/s。

根据一次风质量和能量平衡方程，磨煤机入口一次风质量流量和温度的表达式如下：

qm,air=qm,L+qm,H

(5)

(6)

式中：cp,a为空气比热容，J/(kg·K)；tL和tH分别为冷一次风和热一次风的温度,℃；qm,L、qm,H分别为冷一次风和热一次风质量流量，kg/s。

(7)

式中：θCM为原煤水分含量；tout为磨煤机出口风粉混合物温度；K13和K15为待定的模型参数。

若要对原煤水分含量进行估计，则可将其当成一个没有动态的状态：

(8)

磨煤机内部能量平衡方程如下：

(9)

I=K6mpf+K7mc+K8

(10)

式中：I为磨煤机电流，A；K1～K9、K12、K14为待定的模型参数。

根据流体动量定理，磨煤机出入口压差一方面是由阻力造成的，另一方面是携带煤粉造成压力下降，因此出入口压差p的表达式为：

(11)

式中：K16～K18为待定的模型参数。

综上所述，磨煤机模型如下：

(12)

式(12)所建立的模型本质上是磨煤机正常运行工况下(40%～100%负荷)的非线性模型，当工况发生变化时，该模型仍适用。

根据磨煤机特征参数和电厂实际测点位置，模型输入参数有入口一次风质量流量qm,air、入口一次风温度tin、以给煤机瞬时流量作为磨煤机入口原煤质量流量qm,c；模型输出参数为磨煤机电流I和出口风粉混合物温度tout；K1～K18为模型参数；其他变量为磨煤机状态参数。

1.3 基于遗传算法的模型参数辨识

基于现场运行数据，采用遗传算法对磨煤机模型中的模型参数K1～K18进行辨识。其中现场运行数据选择机组从45%负荷升至90%负荷过程中磨煤机的实际运行数据。

1.3.1 编码

编码是将问题的可行解映射到遗传算法搜索空间的过程，由于待定模型参数的解空间为实数，因此采用连续的浮点数编码。

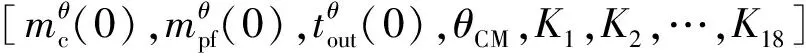
(13)

1.3.2 适应度函数

遗传算法是模拟自然界“优胜劣汰”的规则，因此在求解待定模型参数时，需要一种判别一组编码值优劣的方法。采用预报误差性能指标[11]来评价给定参数下模型的好坏程度：

(14)

其中，

l(t,α,ε)=εTΛε

(15)

ε(t,α)=zN(t)-z(t,α)

(16)

式中：N为辨识所用数据集中测量数据个数；zN为辨识所用的数据集；z(t,α)为模型在t时刻的输出预报值；ε(t,α)为t时刻的预报误差；ε为整个时段预报误差矩阵；Λ为误差权矩阵。

将式(14)～式(16)应用于磨煤机灰箱模型可得到归一化性能指标：

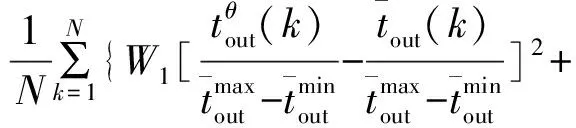
(17)

式中：各物理量上方“-”表示该物理量的实际测量值，上标θ表示物理量的模型预测值，max和min分别表示辨识数据集中实际测量值的最大值和最小值；W1、W2和W3为误差权重。

1.3.3 遗传算法参数的选取

遗传算法的交叉率、变异率和种群个数等参数没有固定的选取方法[12]，采用适应度函数小于给定值作为该算法终止条件。在合理的范围内，这些参数主要影响遗传算法的运算速度，对最终结果并无太大影响。采用实验方法调整这些参数，使程序收敛到最终结果的时间在可接受范围内。最终得到的遗传算法参数如表1所示。

表1 遗传算法参数

基于遗传算法的磨煤机模型参数辨识过程如图1所示。采用某350 MW机组B磨煤机于2015年6月28日14:00—19:00的现场实测数据进行参数辨识，采样周期为1 s。模型参数辨识结果见表2。

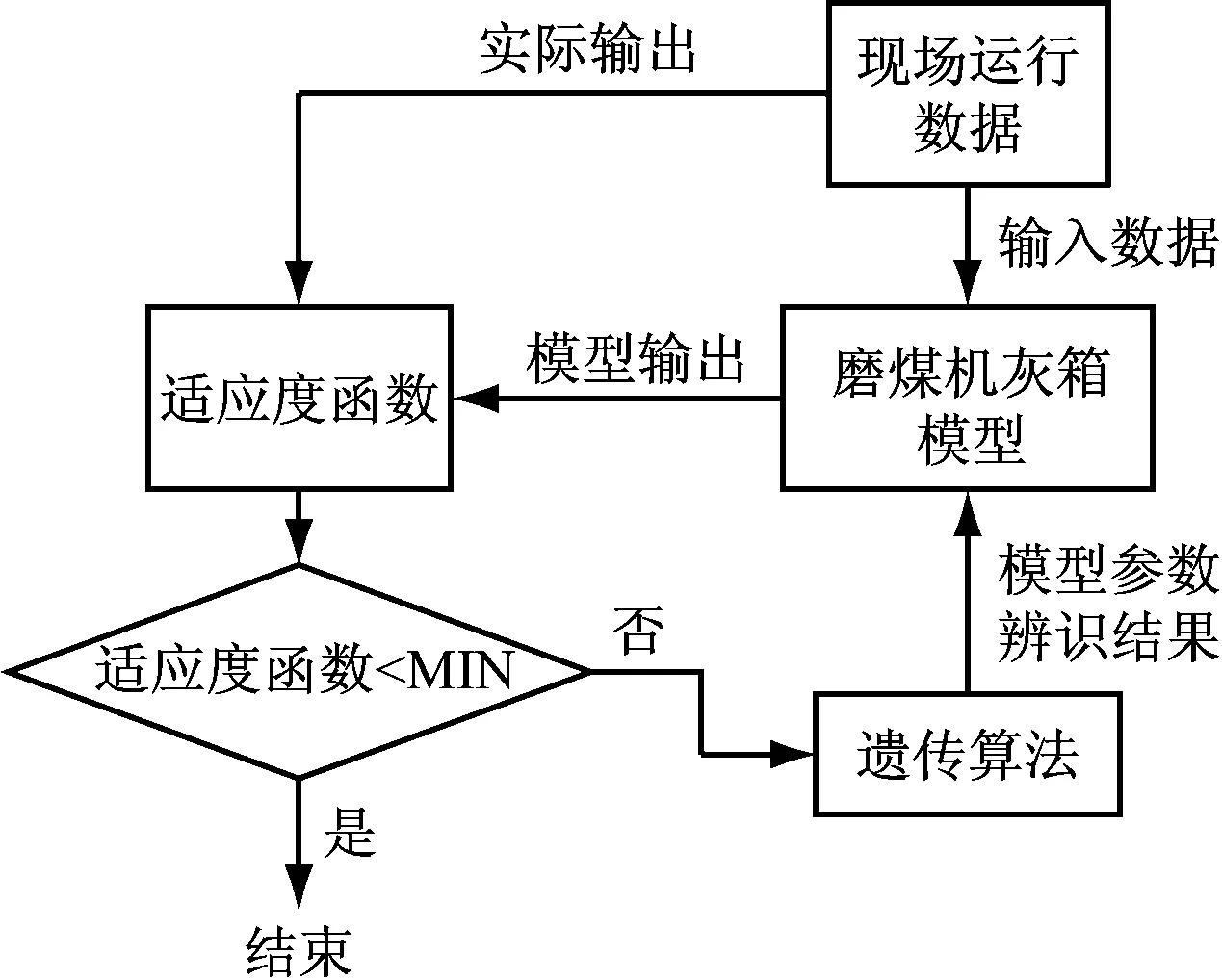
图1 遗传算法辨识模型参数流程图

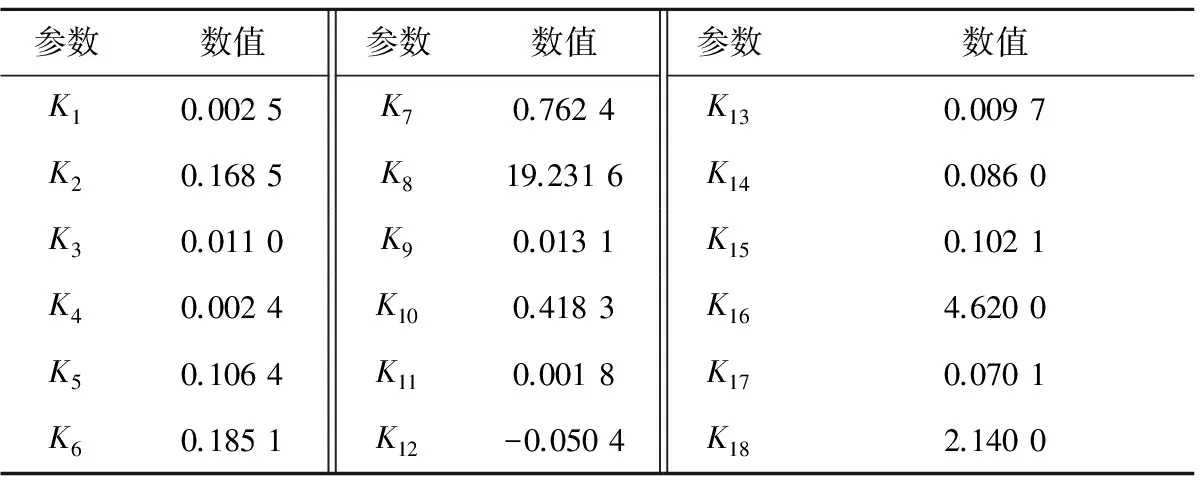
参数数值参数数值参数数值K10．0025K70．7624K130．0097K20．1685K819．2316K140．0860K30．0110K90．0131K150．1021K40．0024K100．4183K164．6200K50．1064K110．0018K170．0701K60．1851K12-0．0504K182．1400

1.4 模型检验

为了验证模型结构及模型参数辨识结果的准确性，选择了同一磨煤机2015年7月6日的实际运行数据来检验模型的准确性。为了检验模型在全工况下的适用情况，选择工况变化较大的数据样本来检验模型。在所选数据范围内，机组在50%～80%范围内变负荷运行。模型预测值与实际测量值的比较如图2所示。

从图2可以看出，模型预测值与实际测量值吻合较好，说明所建立的灰箱模型是可靠的，能够较好地描述磨煤机的工作过程。

2 基于数据残差和小波变换的中速磨煤机故障检测

2.1 故障检测流程

基于所建立的中速磨煤机正常运行状态模型，依据实际测量值与模型模拟正常运行状况的预测值偏差即残差进行故障检测。当变工况运行时，模型能够较好地跟踪实际测量值(见图2)，发生故障时能够得到有效的残差，因此本文方法适用于磨煤机变工况条件下的故障检测。

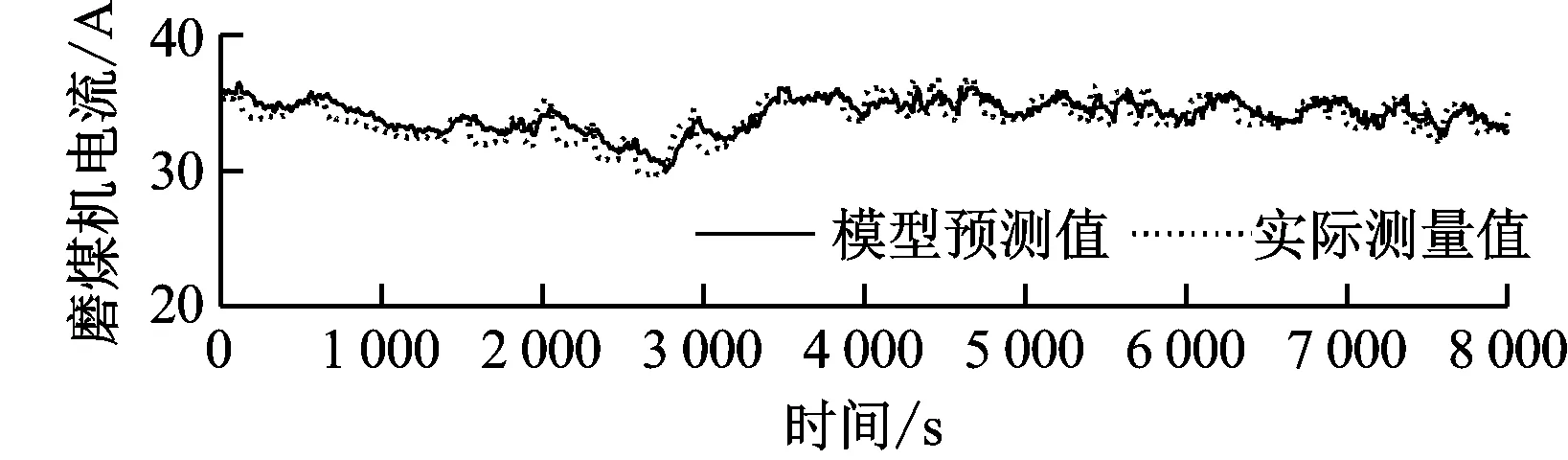
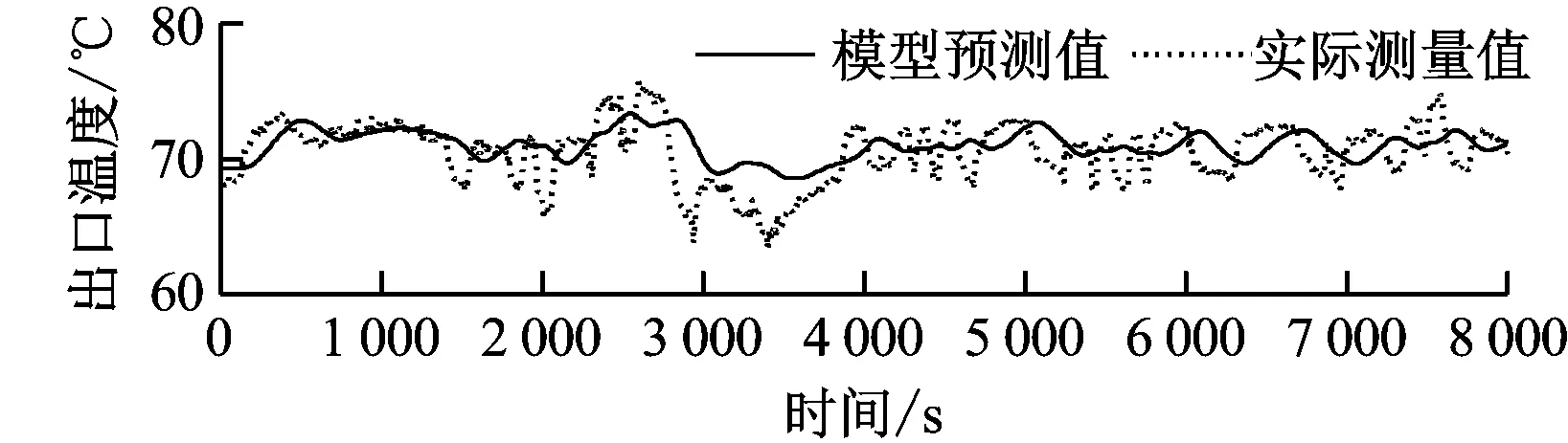
图2 实际测量值与模型预测值的对比

由于磨煤机碾磨物理过程的复杂性，建模误差在所难免。此外，受到各种干扰因素的影响，以及测量过程也存在误差，仅依据残差的绝对值是否超出设定的阈值无法及时准确地检测出故障。笔者通过对一段时间数据的残差曲线进行多尺度小波分解，根据分解后曲线斜率的大小来判断故障是否发生，从而实现对磨煤机故障的早期检测，其流程图如图3所示。

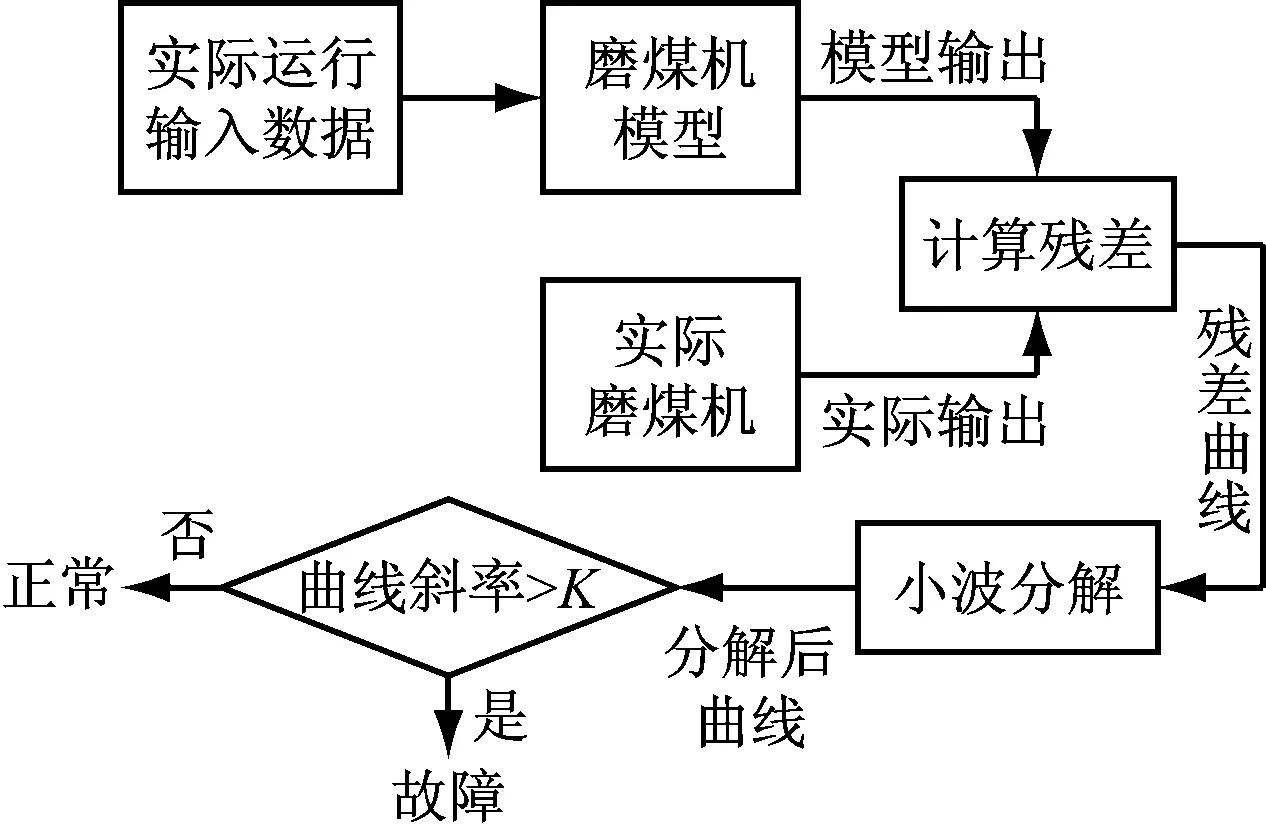
图3 故障检测流程图

2.2 中速磨煤机故障模拟及数据残差生成

选取磨煤机出口堵粉、少煤或断煤和煤粉自燃3种常见故障为算例来阐述计算过程。该方法对其他故障也适用，因为故障的发生总会导致磨煤机相关过程参数偏离正常值，进而获得残差，并用于进行故障检测，之后可以根据每种故障的固有特征，利用随机森林算法诊断出故障类型。

由于缺乏磨煤机故障样本数据，因此笔者在分析各类磨煤机故障特征及其产生原因的基础上，利用所建立的灰箱模型并进行相应修改后，对各类故障进行模拟，进而获得残差数据。

2.2.1 少煤或断煤故障模拟

在发生少煤或断煤故障时，给煤机实际转速未变，但进入磨煤机的给煤量减少。根据该故障特征，建立中速磨煤机故障模型时需在正常模型基础上增加少煤或断煤故障模块。该模块在故障发生后的一段时间内，通过修改给煤量值使其骤减或逐渐减小到零或一个较低的值。

少煤或断煤故障仿真曲线如图4所示。由图4可知，故障发生后，磨煤机给煤量减少，出力下降，进而使磨煤机电流减小；一段时间后，由于没有原煤的供给，内部存煤量逐渐下降，磨煤机内煤粉水分蒸发带走的热量减少，造成出口温度逐渐升高；同时内部存煤量的减少使得磨煤机内阻力降低，出入口压差降低。因此故障模拟结果与真实故障特征是一致的。相应的残差曲线见图5。

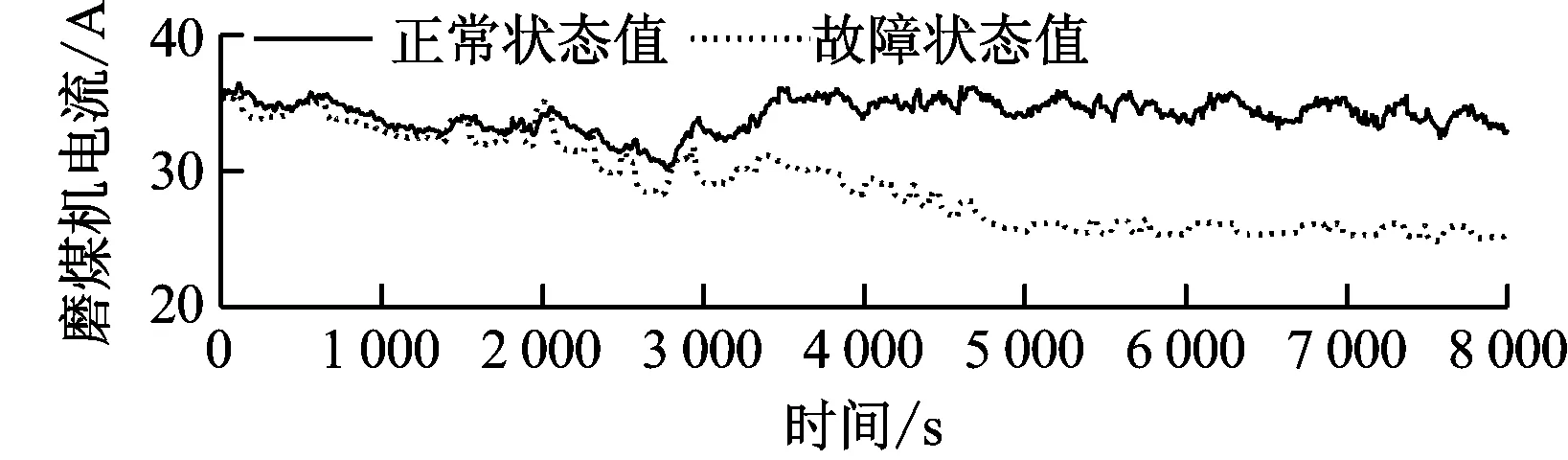
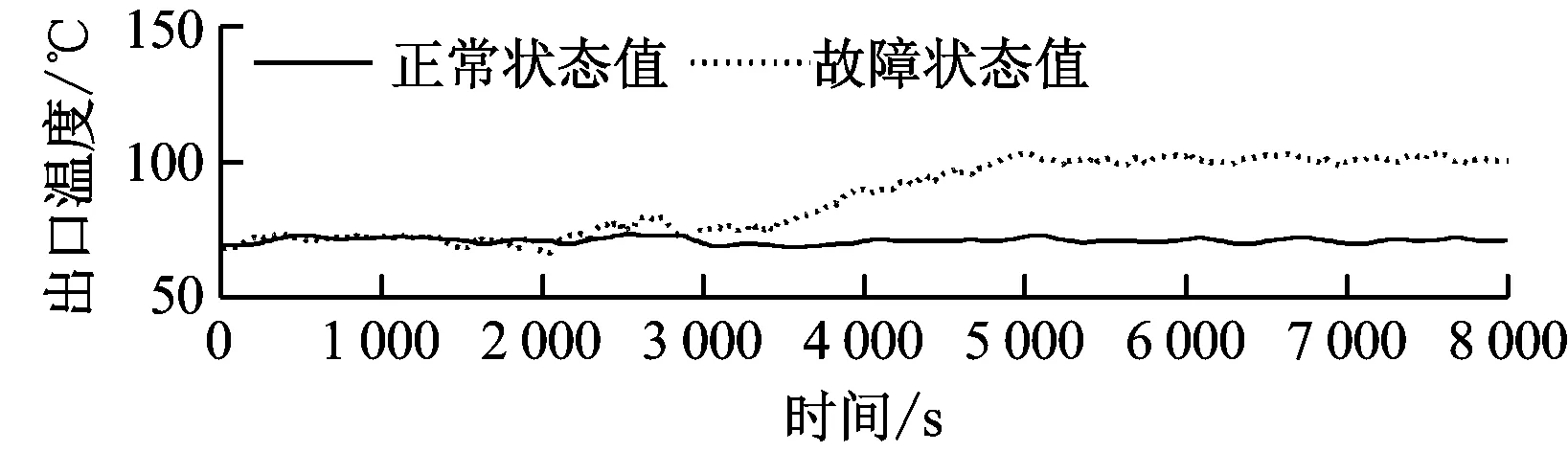
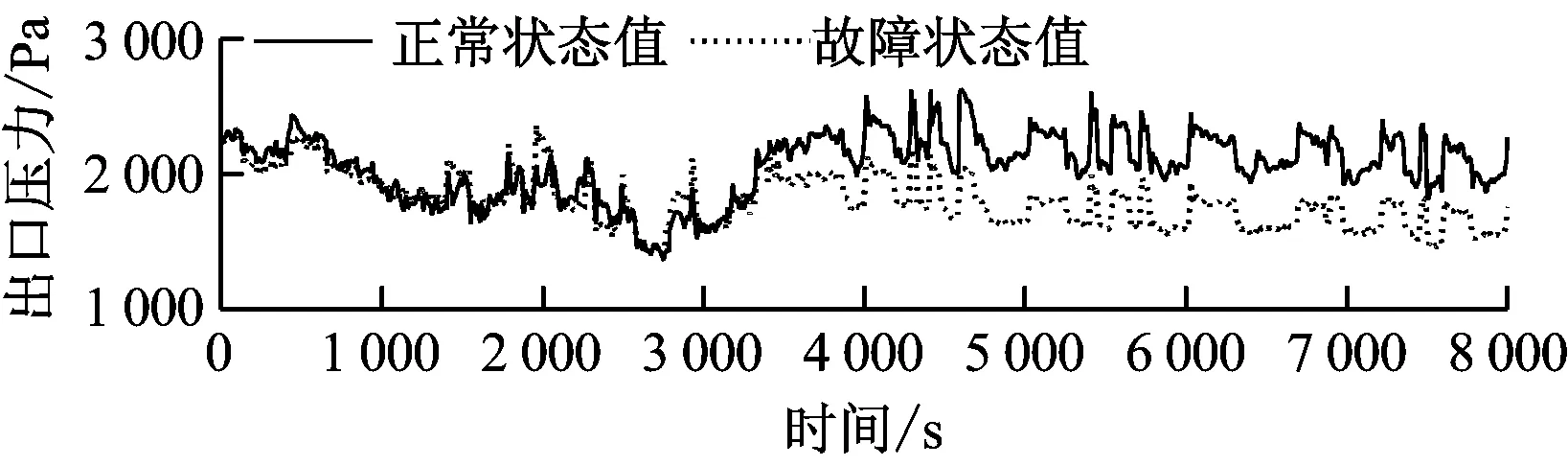
图4 中速磨煤机少煤或断煤故障状态和正常状态运行参数曲线

图5 中速磨煤机少煤或断煤故障残差曲线

2.2.2 出口堵粉故障模拟

出口堵粉故障是由于磨煤机与炉膛之间的压差较低造成煤粉不能及时吹出，煤粉潮湿等原因造成出口送粉管堵塞。主要表现为流通阻力增大，压差增大。在模拟该故障时，增加了一个局部阻力点，即磨煤机出入口压差乘以故障阻力系数ξ。

磨煤机出口堵粉故障仿真曲线如图6所示。由图6可知，仅出口压力下降，磨煤机电流、出口温度无变化，与真实故障发生时的特征一致，因此故障仿真结果是合理的。相应的残差曲线见图7。

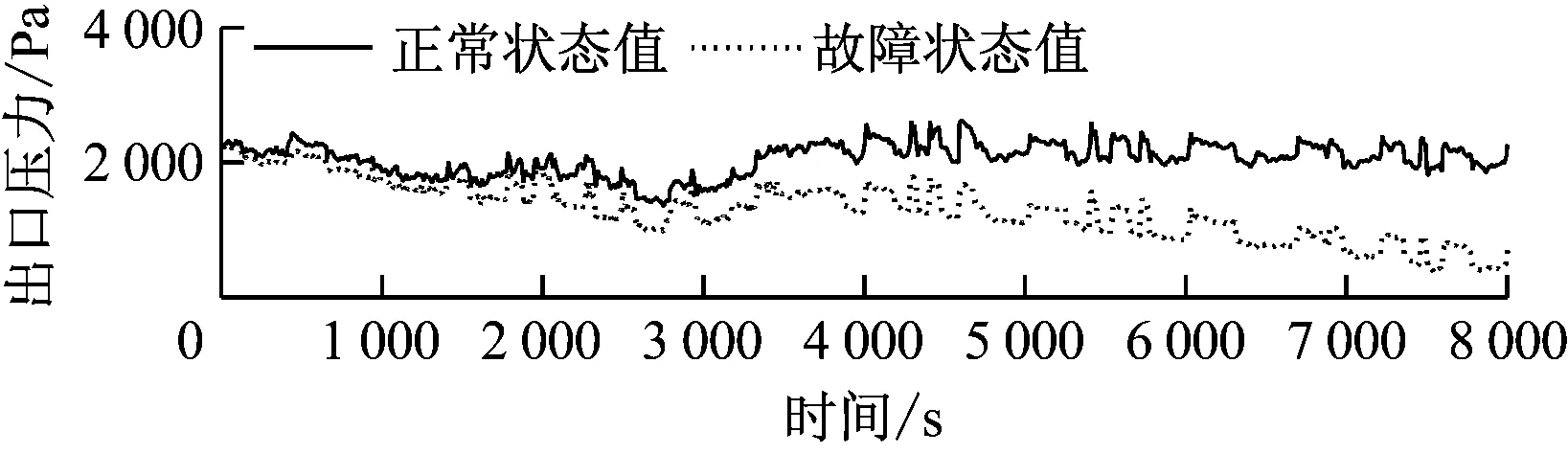
图6 中速磨煤机出口堵粉故障状态和正常状态运行参数曲线

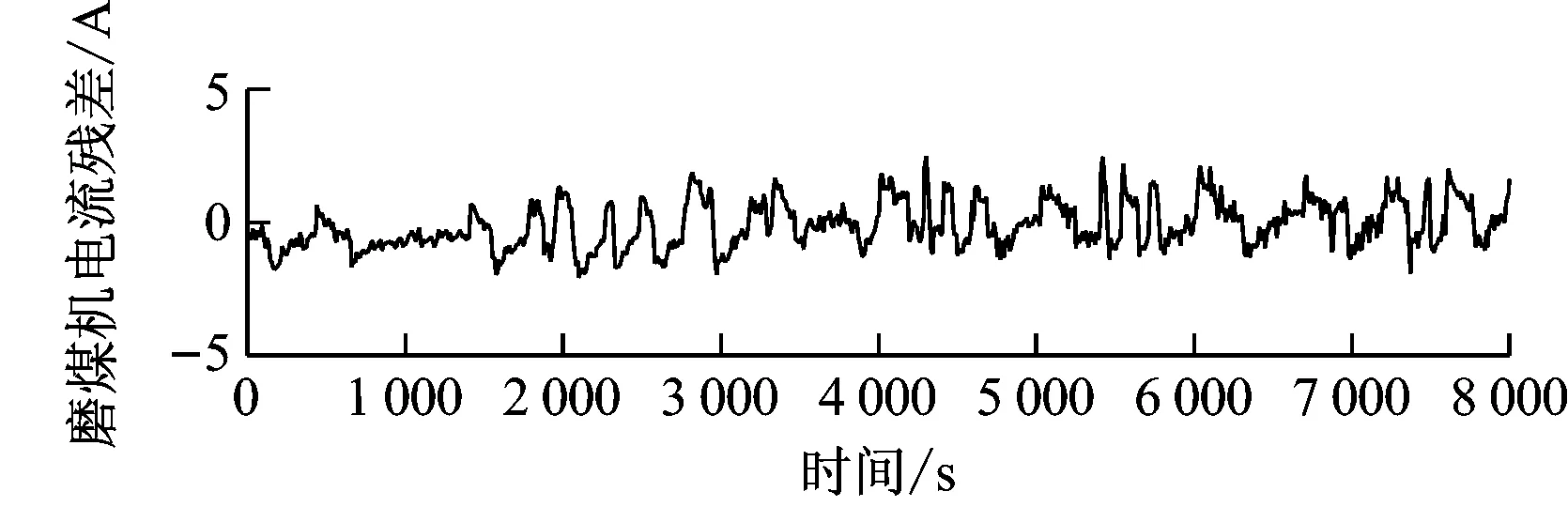
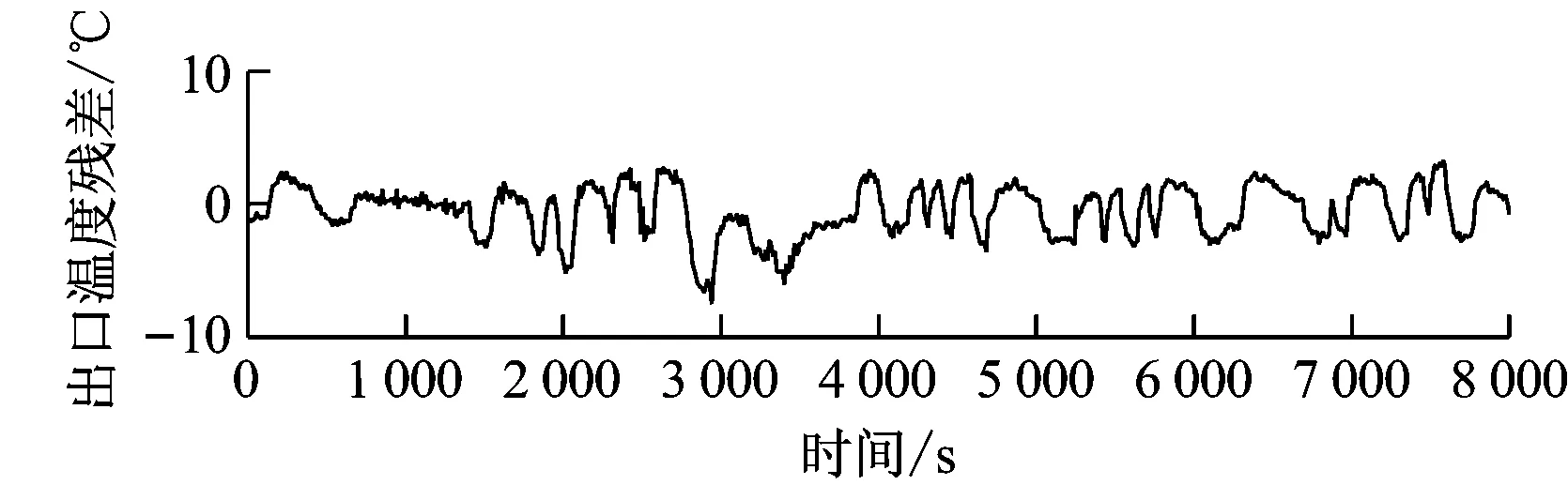
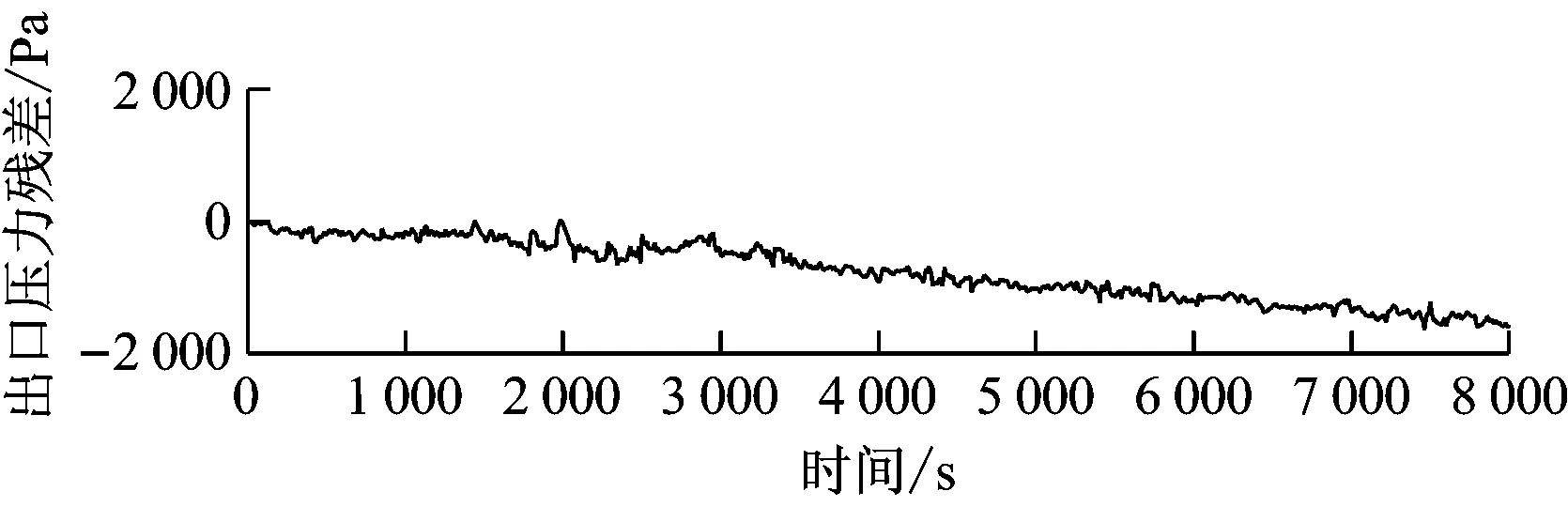
图7 中速磨煤机出口堵粉故障残差曲线

2.2.3 煤粉自燃故障模拟

假设自燃由少量煤粉开始，并逐渐扩散。对该故障进行仿真时，在能量平衡方程上增加煤粉自燃发热量ΔQ。

ΔQ=mt·Qnet

(18)

式中：mt为t时刻自燃煤粉质量，kg；Qnet为煤粉低位发热量，kJ/kg。

煤粉自燃故障仿真曲线如图8所示。由图8可知，煤粉自燃不影响碾磨过程，故磨煤机电流、出口压力基本没有变化，仅出口温度有较大幅度的升高，故障模拟结果与该故障的定性分析吻合。相应的残差曲线见图9。

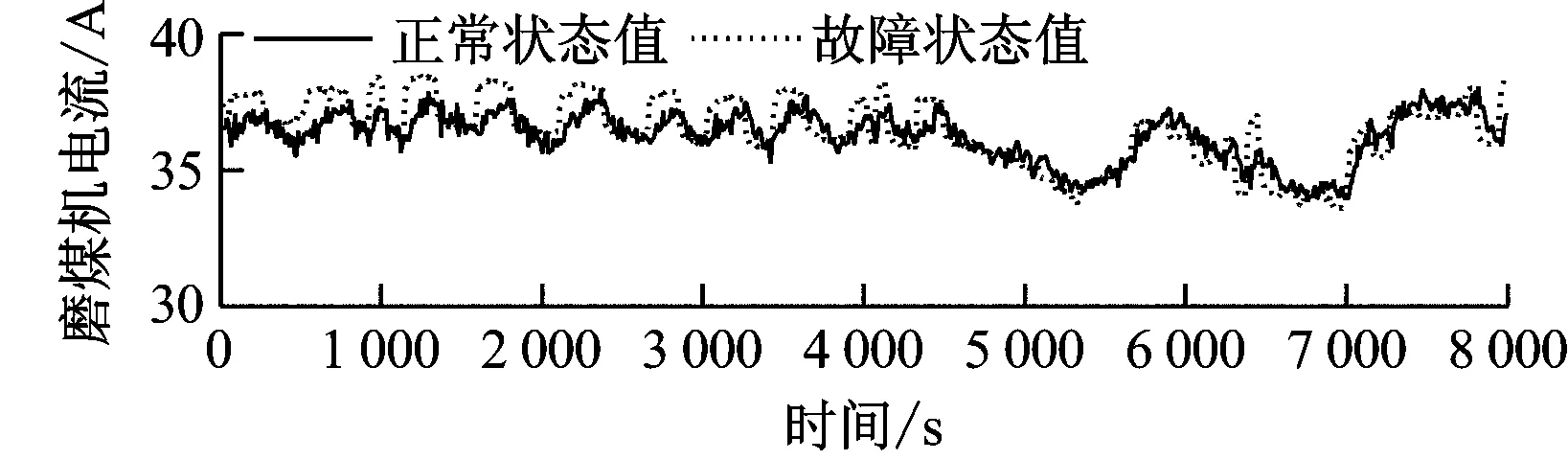
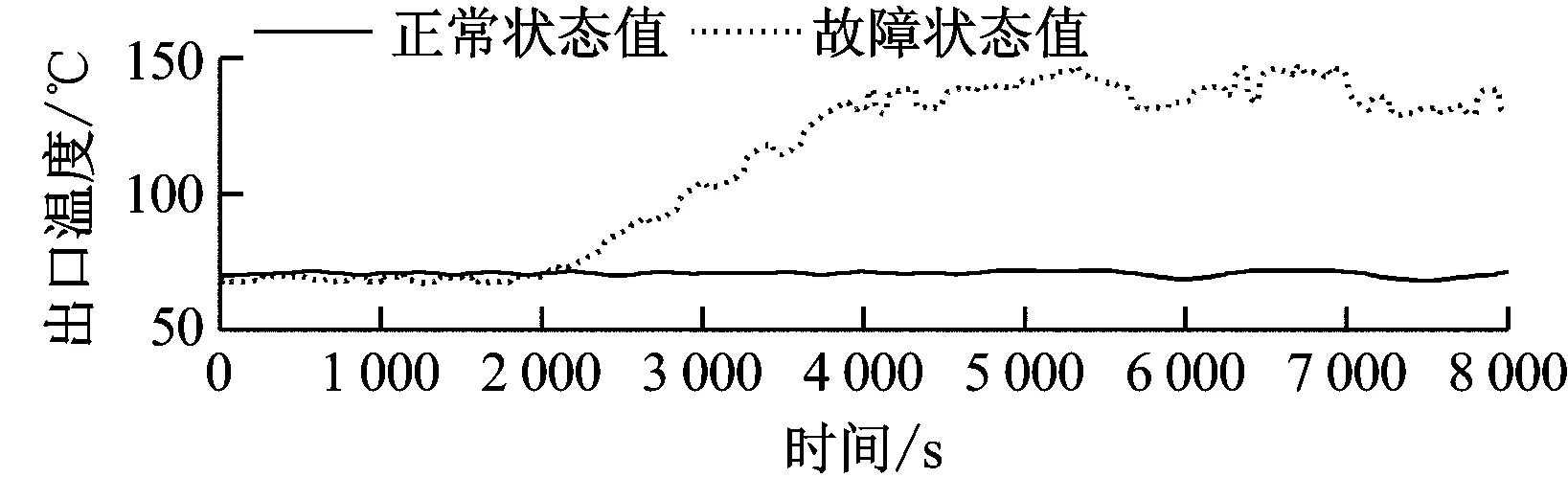
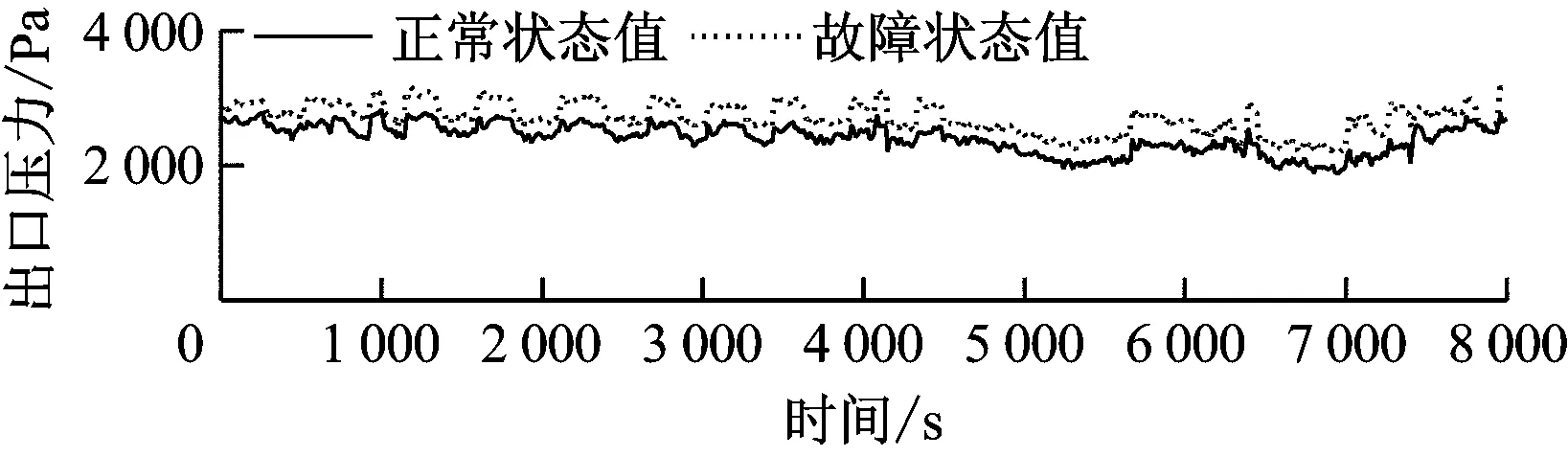
图8 中速磨煤机煤粉自燃故障状态和正常状态运行参数曲线

Fig.8 Operating parameters of the medium-speed coal mill under spontaneous combustion fault and normal conditions

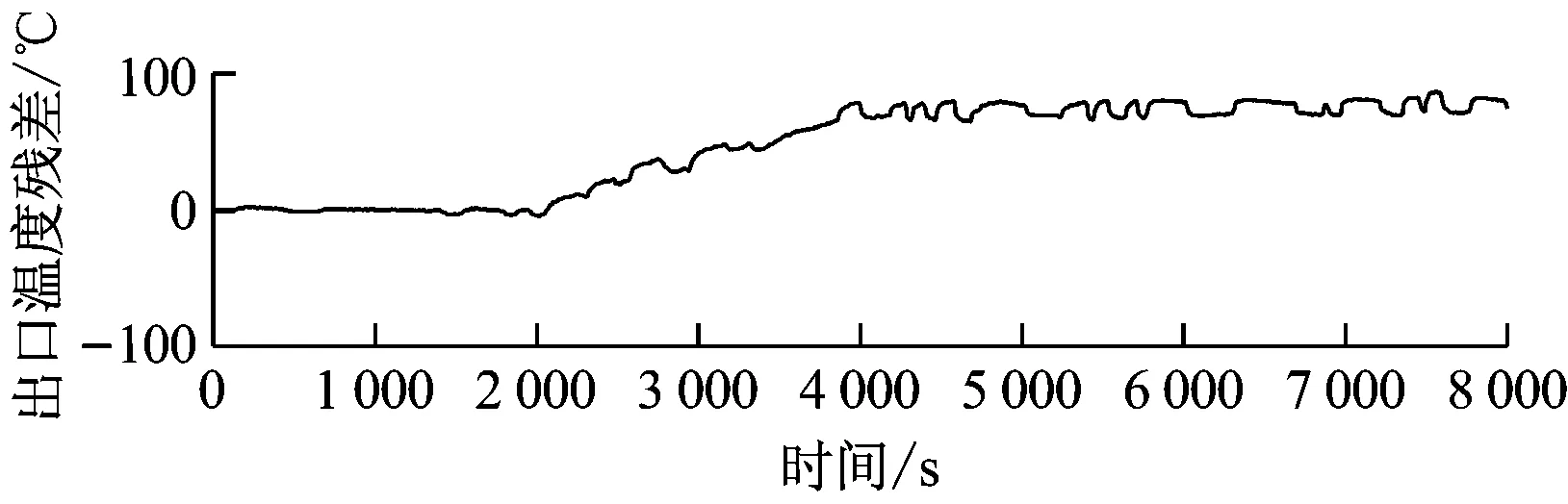
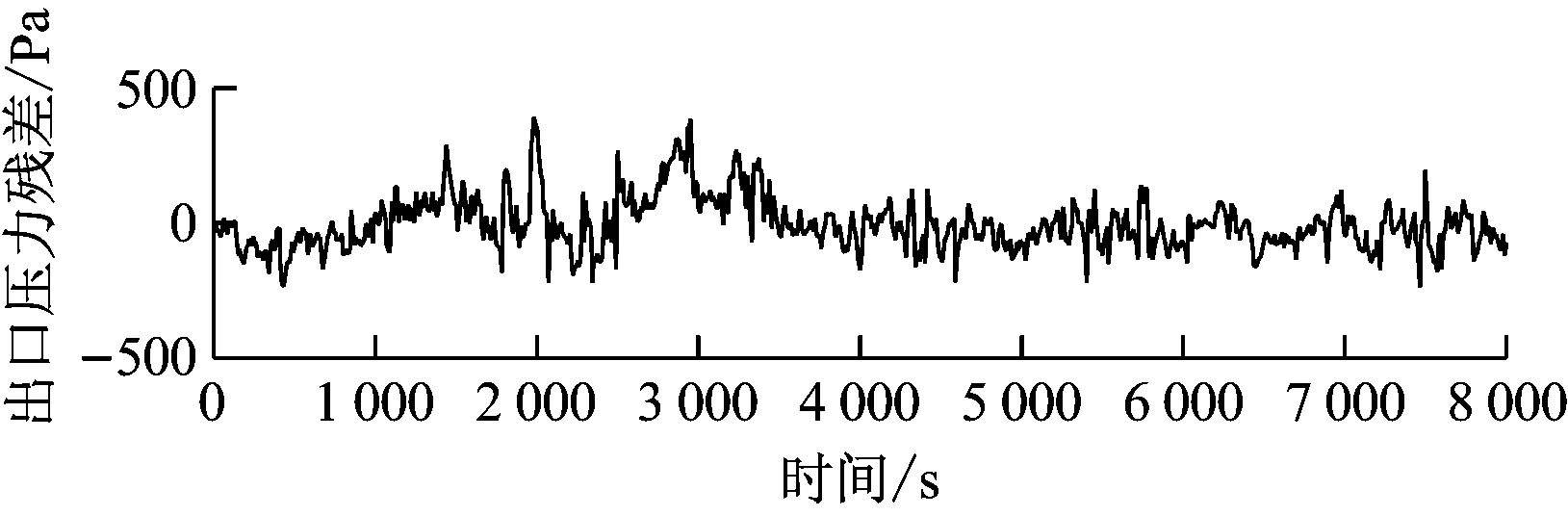
图9 中速磨煤机煤粉自燃故障残差曲线

2.3 基于小波变换的故障检测

2.3.1 最佳小波基的确定

小波函数具有多样性，小波变换需要根据分析对象来选择最适用的小波基及分析尺度，且选择结果不唯一[13]。每个小波基的时频特征各不相同，因此，选择的小波基及分析尺度不同可能得出不同的结果[9, 14]。目前，对最佳小波基的选取尚无较好的数学方法，通常是根据小波基函数的性质、待检测信号的特征和信号处理的目的等，凭经验选取最佳小波基。小波基与被处理信号之间的相似程度通过小波系数的大小来体现[15]。采用实验方法分析若干种常用的小波基，通过小波系数来得到每种输出信号小波变换所用的最佳小波基，结果见表3。

表3 残差信号小波变换选取的最佳小波基

2.3.2 基于小波变换的残差信号趋势提取

从故障模拟结果可以看出，当典型故障发生时，磨煤机电流、出口压力和出口温度数据残差有一个或多个出现异常。因此，当任意一个残差信号出现异常时即可认为磨煤机发生故障。残差信号是种种信号的叠加，一部分是模型预测值与实际测量值的偏差信号，含有对故障诊断很有价值的信息；另一部分是由测量和建模产生的误差信号，为噪声信号。正常状态和故障发生初期，偏差信号较小，残差信号的信噪比很低，因此传统降噪方法难以适用。

笔者基于小波变换原理进行偏差信号的趋势提取。首先确定最佳小波基，然后对残差信号进行多层小波分解，舍弃每层的细节，得到变化趋势信号。其中分解层数通过实验的方法来确定，调整小波分解层数，使得正常状态的趋势近似为一条水平线。小波分解出的细节信号为噪声信号或偏差信号的细节部分，由于提取趋势仅关注偏差信号总的变化，忽略其细节部分是合理的。对残差信号的趋势提取如图10～图12所示。

图10 磨煤机电流残差和趋势提取曲线

图11 磨煤机出口温度残差和趋势提取曲线

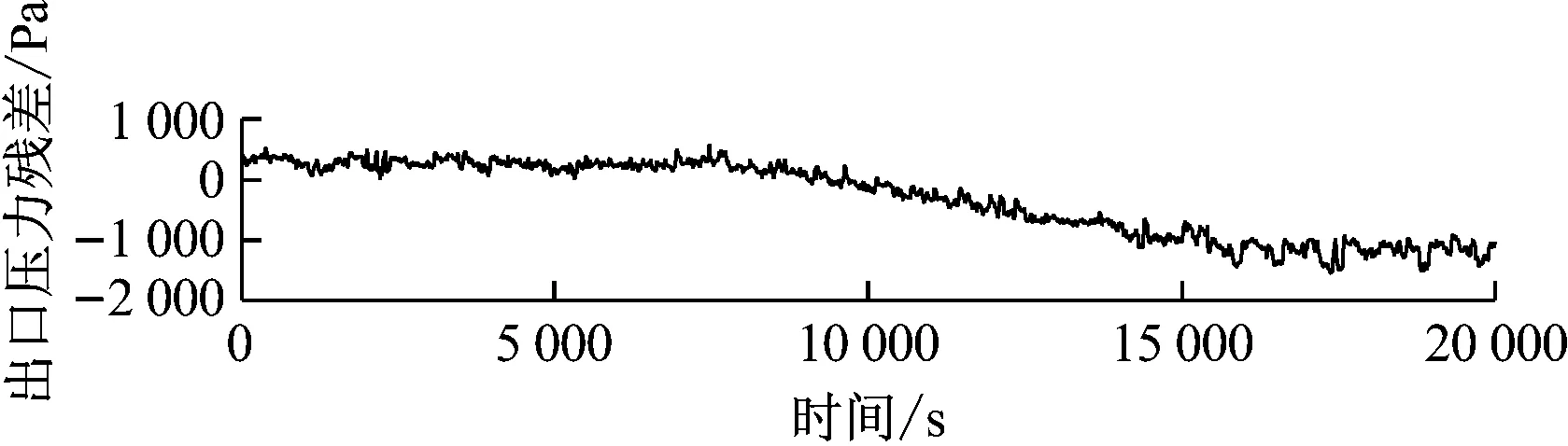
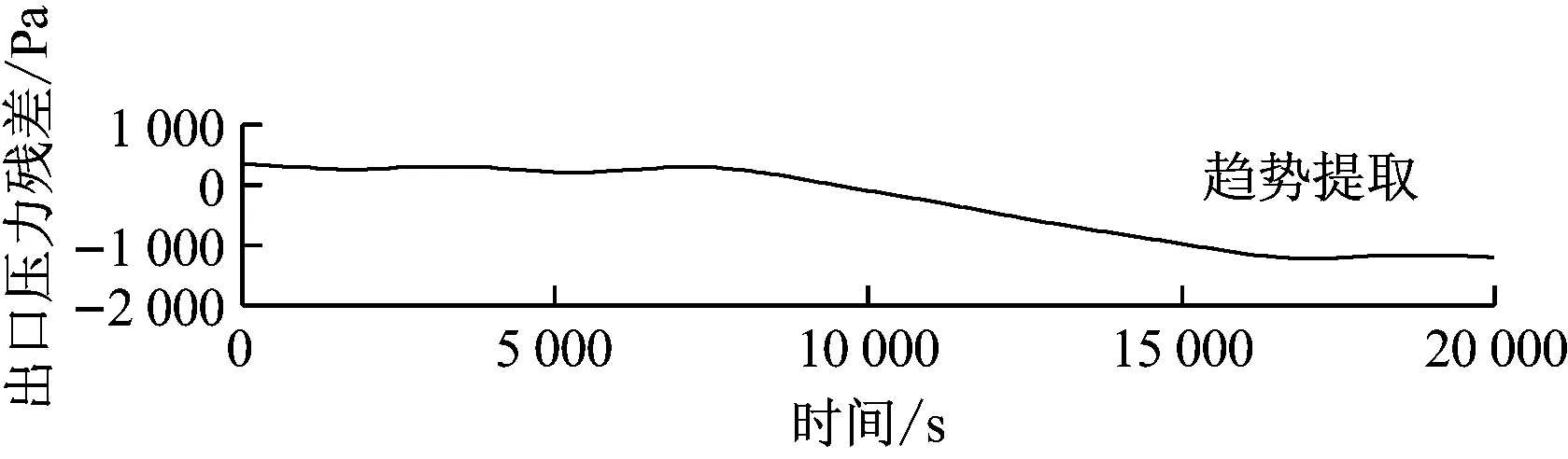
图12 磨煤机出口压力残差和趋势提取曲线

2.3.3 基于趋势提取的斜率阈值故障检测方法

以磨煤机电流残差信号为例，介绍根据斜率阈值法来检测故障的方法，其他残差信号分析方法类似。对趋势信号求一阶和二阶导数(见图13)。由图13可知，当磨煤机电流出现异常时，趋势信号的一阶和二阶导数均出现明显的峰值信号。故障发生时一阶在较短时间内有较大变化，斜率变化幅度数倍于正常状态下的波动，因此可以设置一个一阶导数阈值，当一阶导数超过该阈值时即认为出现故障。

图13 磨煤机电流趋势信号一阶、二阶导数

采用实验方法来选取阈值，对磨煤机正常运行工况下(40%～100%负荷)的数据进行小波变换并求取一阶导数，阈值的计算方法如下：

|Y′|max=K·max(|Y′|)

(19)

式中：K为权系数；Y为残差序列。

阈值的大小通过权系数K来控制，阈值较大时，能降低系统的误报率，但会造成检测出故障的滞后时间增加；阈值较小时，能缩短检测出故障的滞后时间，但是会造成误报率的上升。为了保证较低误报率并兼顾滞后时间，K一般取1.1～1.4。

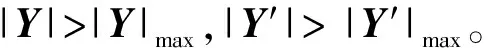
(20)

如式(20)所示，A区为正常工作区，B区仅斜率阈值法能检测出故障，D区仅绝对值阈值法能检测出故障，C区中2种方法均能检测出故障。从图14可以看出，有大量故障工况点落在B区，即这些故障点用斜率阈值法能实现故障检测，而用绝对值阈值法则不能，因此斜率阈值法能检测出更多的故障点，具有更好的灵敏性。

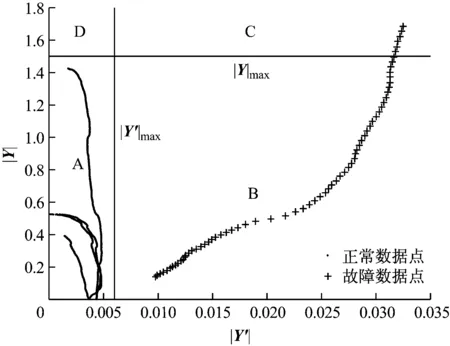
图14 斜率阈值法与绝对值阈值法灵敏性的比较

2.3.4 在线故障检测实例分析

为了确保故障检测结果的准确性，保证足够的数据量，设定小波窗的长度为20 min，故障检测周期为5 min，即小波窗每5 min移动一次。

以中速磨煤机煤粉自燃故障磨煤机出口温度信号为例进行分析，其他故障类型分析方法类似。其故障检测结果见图15和图16，分别为正常状态、故障发生早期连续2个小波窗的分析结果。小波变换后计算一个小波窗时间趋势信号的一阶导数，如果连续5个点超过斜率阈值，则认为发生故障。斜率阈值取正常状态下3～5 h趋势信号一阶导数最大值的1.2倍。由图15可知，正常状态下不会发生误判。图16中，在故障发生早期就能检测出故障，按照图14所示方法进行分析，斜率阈值法比传统的绝对值阈值法提前了87个数据点，约15 min(不同情况故障发生速率不同，该数值略有差别)。因此，故障检测实例分析的结果与之前的结论相同，证明了所提出的斜率阈值法在故障检测上具有良好的准确性。

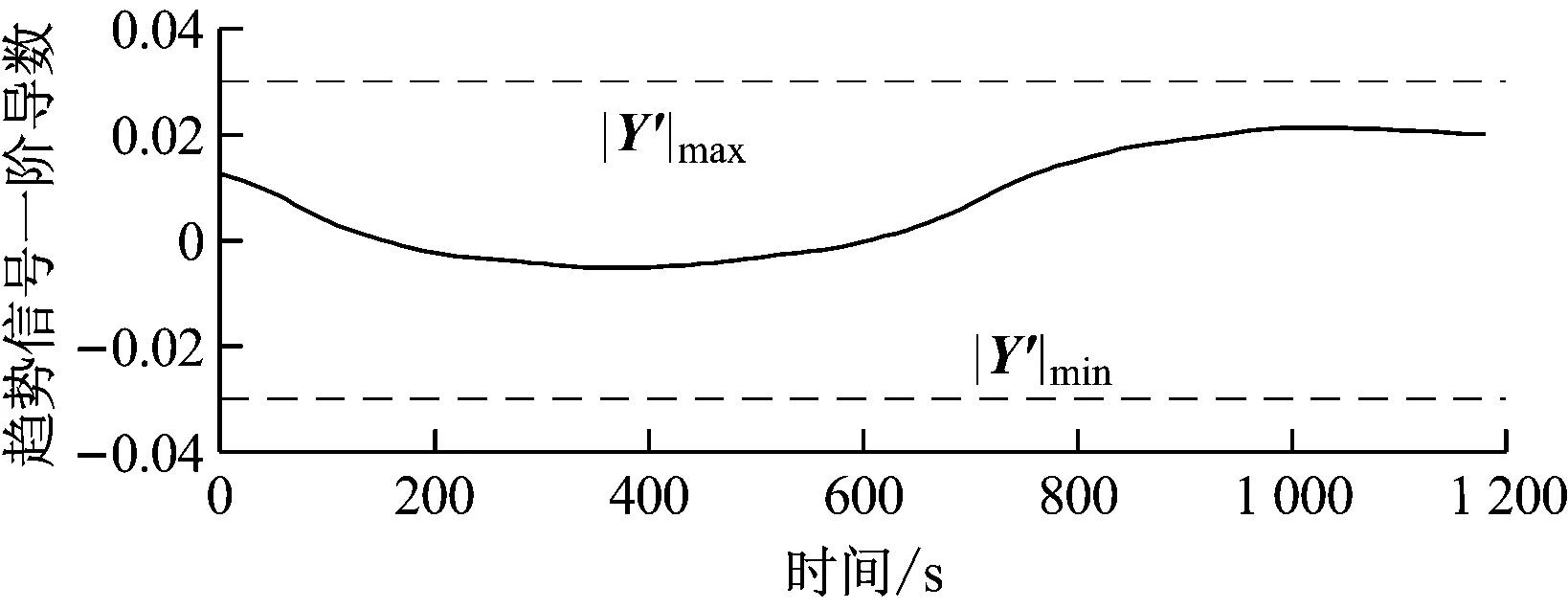
图15 正常状态小波窗分析结果

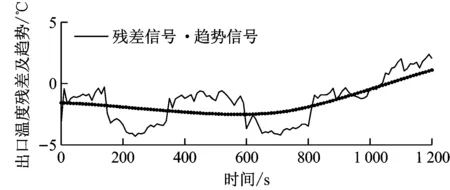
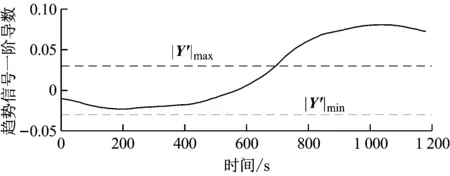
图16 故障发生早期小波窗分析结果

3 基于随机森林算法的中速磨煤机故障识别

3.1 故障类型判断实现过程

在检测出故障以后，利用随机森林算法来区分故障类型，从而使故障排除更有针对性。

图17中，中速磨煤机故障识别模块由随机森林分类器、分类器的训练器和故障数据库组成。首先由故障仿真模块仿真出中速磨煤机故障，建立初始故障数据库，将该数据库作为训练数据得出随机森林分类器。故障检测模块会检测出实际故障，然后由随机森林分类器判断出故障类型。随着故障诊断系统的投入使用和实际故障数据的不断积累，故障数据库中实际故障数据所占的比例越来越高，而其每扩大一定的数据量会对随机森林分类器进行更新，随着实际故障数据的积累，随机森林分类器的性能也会逐渐提高。

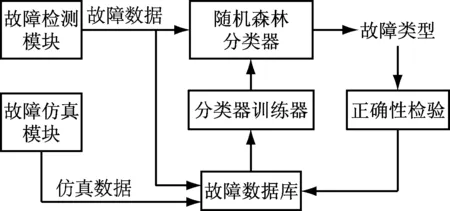
图17 中速磨煤机故障类型判断流程图

随机森林是一种模型组合和决策树的混合算法，由很多决策树组成，其中任意2棵决策树都是独立的[16]。随机森林算法的原理及训练分类器的步骤如下：

(1) 样本集构造与采样。

选择磨煤机电流、出口压力和出口温度的残差信号、残差趋势信号及趋势信号的一阶和二阶导数为变量，共12个变量。然后将故障数据库中的故障数据和一部分正常数据放入样本集中。

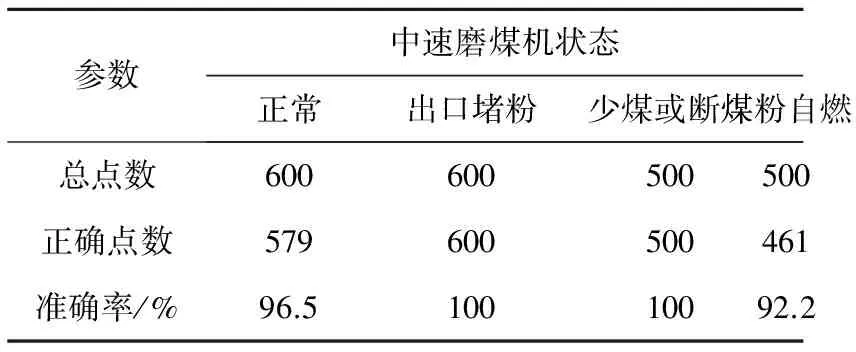
训练决策树的样本由2个随机采样的过程得到，随机森林对输入的数据进行行(数据)和列(变量)的采样。首先进行行采样，从M行中采用有放回的方式随机取出一行，共取M次。这样在决策树构造的时候，每一棵决策树的输入样本都不是全部的样本，不容易出现过拟合。然后进行列采样，从N列中选择n个(n<

(2) 构造决策树。

随机森林中每一棵分类树为二叉树，其生成遵循自顶向下的递归分裂原则，即从根节点开始依次对训练集进行划分；在二叉树中，根节点包含全部训练数据，按照节点纯度最小原则，分裂为左节点和右节点，分别包含训练数据的一个子集。按照同样的规则节点继续分裂，直到叶子节点里所有的样本都指向同一个分类或者无法继续分裂。其中，纯度用基尼指数来度量。

与一般决策树构造不同的是，随机森林所使用的决策树要完全分裂，即每棵树最大限度地生长，不进行任何修剪。因为一般决策树剪枝是为了解决可能出现的过拟合问题，而在随机森林算法中，之前的2个随机采样过程保证了随机性，一般不会出现过拟合问题。

(3) 构造随机森林分类器。

利用步骤(2)的规则构造一组决策树组成随机森林，对于单条数据，每棵决策树都会给出一个分类结果，2棵决策树的结果可能不同。对于该条数据，最终的分类结果采用决策树等权值投票原则，票数最多的结果即为随机森林分类器的结果。其中，由于数据特征即故障种类是有限的，决策树可能得出的结果种类也是有限的，并且远小于决策树的个数，故该投票方法是合理可行的。

3.2 故障类型判断准确性验证

为了检验故障类型判断分类器的准确性，采用故障仿真模块针对中速磨煤机常见故障进行了仿真，得到训练集和测试集2组数据。训练集作为历史运行数据放入故障数据库中，用于训练随机森林分类器；测试集用来模拟实时运行数据，检测故障类型判断的结果。其中每组数据包含正常状态600个数据点、磨煤机出口堵粉600个故障点、磨煤机少煤或断煤500个故障点和磨煤机内煤粉自燃500个故障点，每种状态数据点均由10个独立的连续时间段的数据构成。

训练集的质量会影响随机森林分类器的训练结果。在训练集样本的仿真生成上，应尽量包含正常状态的全部范围和每种故障类型下不同程度的故障数据。其中正常状态数据越丰富故障漏报率越低，不同故障程度的数据越丰富故障误报率越低。

故障类型的判断结果如表4和图18所示。从表4可以看出，基于随机森林算法的故障类型判断方法仅单个数据点故障类型识别准确率就能够达到90%以上。前面设定了5 min为一个检测周期，采样周期为10 s，则一个故障检测周期新产生30个数据点，认为其中大于24个点判断一致即可识别出故障类型。下面对一个检测周期内故障辨识的准确率进行分析。

表4 中速磨煤机故障类型识别结果

图18 随机森林分类器分类结果

从图18可以看出，识别错误点没有明显的分布规律，即不会由于随机森林分类器的误差出现连续误判的情况，可以认为每个数据点识别的准确与否是相互独立的，则一个检测周期内的数据点判断的准确性服从二项分布。因此一个检测周期内故障类型准确识别率Pc为：

(21)

故障识别错误率Pe为：

(22)

故障未识别率Pn为：

Pn=1-Pe-Pc

(23)

式中：p为单点故障识别准确率。

考虑一定的安全余量，取单点故障识别准确率为90%，得出一个检测周期内的Pc、Pn和Pe如表5所示。从表5可以看出，对一个检测周期内的数据点进行故障类型判断能较为准确地识别出故障类型。虽然有2.58%的故障未识别率，但是基本消除了错判的情况。

表5 故障识别情况表

4 结 论

采用数据与机理分析相结合的方法建立了中速磨煤机系统的灰箱模型。仿真结果表明，该模型具有较高的精度和良好的泛化能力。

在此基础上，利用模型得到了磨煤机输出量的残差数据，并通过小波变换提取残差的变化趋势，提出了基于斜率阈值的故障检测方法。该方法能实现对磨煤机故障的早期诊断。最后利用随机森林算法对故障类型进行识别。仿真实验表明，该方法有较高的故障识别率和识别精度。

[1] 曾德良, 高珊, 胡勇. MPS型中速磨煤机建模与仿真[J].动力工程学报, 2015, 35(1): 55-61.

ZENG Deliang, GAO Shan, HU Yong. Modeling and simulation of MPS medium speed coal mills[J].JournalofChineseSocietyofPowerEngineering, 2015, 35(1): 55-61.

[2] AGRAWAL V, PANIGRAHI B K, SUBBARAO P M V. Review of control and fault diagnosis methods applied to coal mills[J].JournalofProcessControl, 2015, 32: 138-153.

[3] ISERMANN R. Model-based fault-detection and diagnosis-status and applications[J].AnnualReviewsinControl, 2005, 29(1): 71-85.

[4] FAN G Q, REES N W. An intelligent expert system (KBOSS) for power plant coal mill supervision and control[J].ControlEngineeringPractice, 1997, 5(1):101-108.

[5] ODGAARD P F, MATAJI B. Observer-based fault detection and moisture estimating in coal mills[J].ControlEngineeringPractice, 2008, 16(8): 909-921.

[6] GUO Shen, WANG Jihong, WEI Jianlin, et al. A new model-based approach for power plant tube-ball mill condition monitoring and fault detection[J].EnergyConversionandManagement, 2014, 80: 10-19.

[7]WEI Jianlin, WANG Jihong, WU Q H. Development of a multisegment coal mill model using an evolutionary computation technique[J].IEEETransactionsonEnergyConversion, 2007, 22(3): 718-727.

[9] 曾德良, 刘继伟, 刘吉臻, 等. 小波多尺度分析方法在磨辊磨损检测中的应用[J].中国电机工程学报, 2012, 32(23): 126-131.

ZENG Deliang, LIU Jiwei, LIU Jizhen, et al. Application of wavelet multi-scale analysis for wear characteristics[J].ProceedingsoftheCSEE, 2012, 32(23): 126-131.

[10] HAN Xiaojun, JIANG Xue. Fault diagnosis of pulverizing system based on fuzzy decision-making fusion method[M]//CAO Binyuan, LI Futai, ZHANG Chengyi. Fuzzy Information and Engineering Volume 2. Berlin Heidelberg: Springer, 2009: 1045-1056.

[11] LJUNG L. System identification, theory for the user[J].EPFL, 2012, 16(1): 9-11.

[12] 王银年. 遗传算法的研究与应用——基于3PM交叉算子的退火遗传算法及应用研究[D]. 无锡: 江南大学, 2009.

[13] YEN G G, LIN K C. Wavelet packet feature extraction for vibration monitoring[J].IEEETransactionsonIndustrialElectronics, 2000, 47(3): 650-667.

[14] WANG W J, MCFADDEN P D. Application of wavelets to gearbox vibration signals for fault detection[J].JournalofSoundandVibration, 1996, 192(5): 927-939.

[15] 张芸芸. 基于紧致型小波神经网络的六脉波变频器故障诊断研究[D]. 焦作: 河南理工大学, 2011.

[16] BONISSONE P, CADENAS J M, GARRIDO M C, et al. A fuzzy random forest[J].InternationalJournalofApproximateReasoning, 2010, 51(7): 729-747.

[17] LIAW A, WIENER M. Classification and regression by random forest[J].RNews, 2002, 2(3): 18-22.