汽轮机扭振作用下叶片响应及应力计算

杨 昆， 赵鹏程， 顾煜炯， 聂沈斌， 龚明祥

(1.华北电力大学 国家火力发电工程技术研究所，北京 102206；2.中广核苏州热工研究院有限公司，江苏苏州 215000)

随着汽轮机容量不断增加，轴系长度与汽轮机末级叶片长度也在不断加长，当汽轮机轴系发生扭振故障时可能会造成叶片损伤甚至断裂。晏水平等[1]采用数值法得到了轴系扭振作用下叶片的响应；吕方明等[2]对汽轮机长叶片弯曲与轴系扭振耦合振动进行研究，给出了不同模型的模态振动特征。

笔者以某国产600 MW汽轮发电机组低压缸末级叶片为例，建立转子-叶片的耦合扭振模型，在轴系发生扭振故障时对叶片的响应进行仿真，并计算得到叶片的应力。

1 叶轮固有特性分析

图1给出了某国产600 MW汽轮发电机组低压缸末级叶片。其中叶片叶高为1 092.2 mm，根部半径为927.1 mm，转动惯量为43.41 kg·m2，叶轮中叶片数为85，叶片自带“Z”型干摩擦阻尼围带。叶片装配时围带间的相对位置如图2所示，围带间间隙δ为0.55 mm，围带工作面与切向的夹角α为30°。

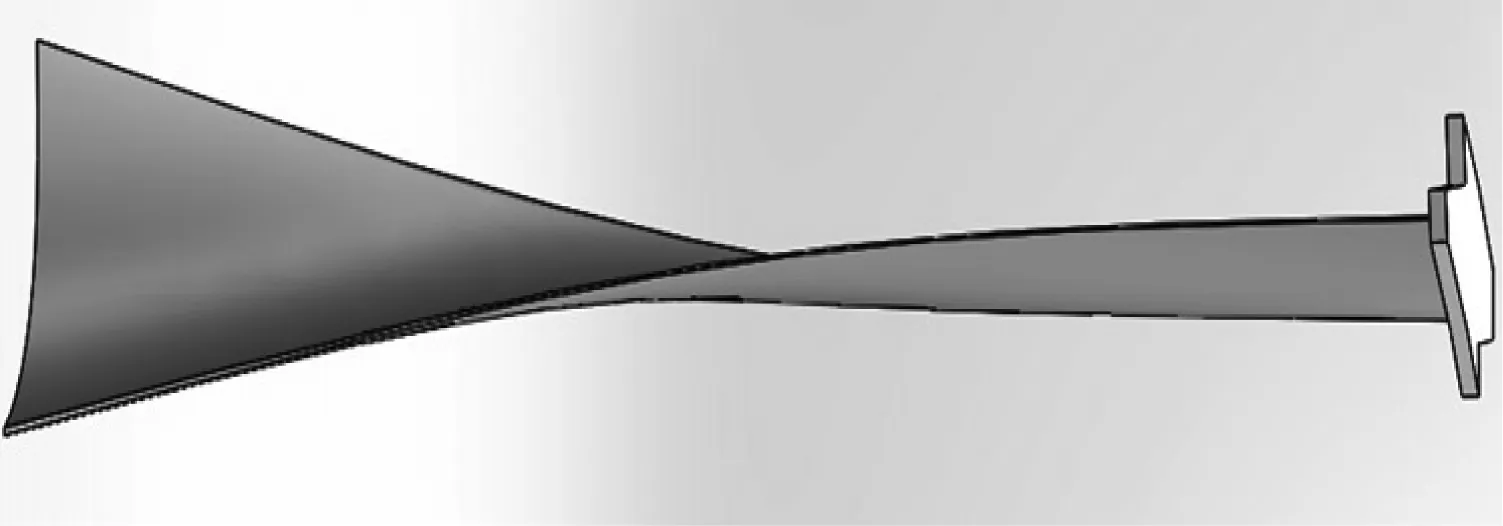
图1 600 MW汽轮发电机组低压缸末级叶片示意图

Fig.1 Schematic diagram of LP last stage blades in a 600 MW turbo-generator set

图2 围带连接示意图

利用Ansys软件建立叶轮的有限元模型(见图3)，对叶轮的固有特性进行分析，得到叶轮伞型振动中前两阶周向振动的振型，如图4和图5所示,其对应的固有频率分别为107.7 Hz和403.3 Hz。

图3 叶轮有限元模型

图4 第一阶周向振动叶片振型

图5 第二阶周向振动叶片振型

2 转子-叶片耦合扭振模型

汽轮发电机组轴系可以模化为由扭转弹簧和轮盘组成的集中质量扭振模型。为与叶片的振动模型相配合，该扭振模型可以等效化为x方向(x方向为汽轮机转子周向，但等效成某一瞬间振动横向方向)的振动模型(以下简称为等效模型)，等效方法如下：

(1)

同理，施加在轴系上的电磁力矩和蒸汽力矩也可用下式等效化为x方向的作用力：

F(t)=T(t)/r

(2)

式中：F(t)为t时刻x方向的等效作用力；T(t)为电磁力矩或蒸汽力矩；r为发电机绕组半径。

在将轴系扭振模型等效化为x方向的扭振模型之后，可将叶片模型与其所在的轴段模型相结合，形成轴段-叶片子系统模型，如图6所示，其中m0为叶轮所在轴段等效质量，m1～mn为整圈叶片等效模型中各质量块的等效质量。该模型两端为自由端，围带对叶片的作用力以系统外力的形式施加在代表叶片顶端的质量块上，其大小与叶片顶端-叶片根部在x方向的位移差成正比；轴系对该子系统的扭矩同样以系统外力的形式施加在代表轴段的质量块上。

图6 轴段-叶片子系统模型

Fig.6 Vibration mode of the rotor section-blade disk sub-system

将轴系中各轴段的等效质量块用相应的等效弹簧连接起来，可得到整个轴系-叶片系统的弹簧-质量模型，如图7所示，其中y方向和z方向分别为汽轮机轴向和径向,K1为高压转子与中压转子的连接刚度。

图7 轴系-叶片系统弹簧-质量模型

3 转子-叶片耦合扭振仿真分析

以某国产600 MW汽轮发电机组轴系为例，建立转子-叶片耦合扭振模型。该机组轴系结构如图8所示，由高压缸、中压缸、2个低压缸和1个发电机组成。轴系扭振固有频率见表1。

图8 轴系结构示意图

阶数1234频率/Hz13．423．826．5113．1

将轴系模化为图9所示的集中质量模型，该模型参数如表2所示，其中HP表示高压转子，IP表示中压转子，ALP和BLP分别表示A和B 2个低压转子，GEN表示发电机转子。该机组低压缸末级叶片即为图1中的叶片，每个低压缸有2组末级叶片。除低压缸末级叶片外，其他叶片的扭振固有频率较高，不易与轴系扭振发生耦合作用，可作为附加转动惯量处理，因此笔者只考虑了末级叶片与轴系的耦合振动特性，若考虑其他叶片与轴系的耦合振动时,可根据本文的方法将转子模化为多段集中质量模型，分别考虑转子与叶片之间的耦合特性，并修正最终的计算结果。

图9 汽轮发电机组轴系结构

Fig.9 Shafting structure of turbo-generator sets

表2 轴系结构参数

根据以上方法，可将该机组轴系和低压缸末级叶片模化为如图10所示的x方向耦合扭振模型，该模型参数如表3所示,其中mm1～mm5分别为高压转子、中压转子、低压转子A、低压转子B和发电机转子的质量，K2～K4分别为中压转子与低压转子A的连接刚度、低压转子A与低压转子B的连接刚度和低压转子B与发电机转子的连接刚度，RM1～RM5为各转子轴段的半径，Rm1和Rm2为叶片位置处半径。需要指出的是低压缸两边是双排气，两边各有一组末级叶片，一圈末级叶片能够等效为一串质量块，两圈末级叶片就等效为2串质量块，但由于同一转子上两端的末级叶片形状相同，等效化后的2串质量模型也相同，这样就很容易把2个质量模型进一步合并为1个质量模型，本算例中的m1和m2即为合并后的等效质量。

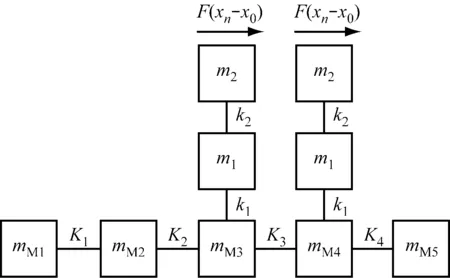
图10 轴系-叶片耦合扭振模型

参数mM1/kgmM2/kgmM3/kgmM4/kgmM5/kgm1/kgm2/kg数值2150385024485．1024950．4819398569．51533．4参数K1/(N·m·rad-1)K2/(N·m·rad-1)K3/(N·m·rad-1)K4/(N·m·rad-1)k1/(N·m-1)k2/(N·m-1)RM1/m数值1．310×1081．538×1081．825×1082．207×1082．283×1095．573×1091参数RM2/mRM3/mRM4/mRM5/mRm1/mRm2/m数值10．92710．927111．41012．0193

该机组发电机的额定电流为19 245 A，额定电压为27 kV，电枢电阻为0.001 488 Ω。对其进行两相短路仿真，得到短路过程中发电机的电磁力矩(见图11)。采用Riccati传递矩阵法和Newmark-β法相结合的方法[3]计算得到叶片顶端的位移响应，其响应曲线如图12所示。

对图12中的位移响应结果进行频谱分析，可以得到叶片顶端相对叶片根部位移的频谱特性，如图13所示。

图11 发电机电磁力矩

图12 叶片顶端位移响应

图13 叶片顶端相对叶片根部的位移频谱

Fig.13 Frequency spectrum of the relative displacement between the tip and root

由于叶片随轴系扭振而振动，图13中存在工频和轴系扭振固有频率成分，同时在108 Hz附近出现了一个明显峰值，与叶轮的第一阶周向振动振型一致。由此可见，所提出的转子-叶片耦合扭振模型可以很好地反映轴系和叶片的扭振固有特性，可以用于轴系的扭振分析。

4 扭振下叶片应力计算

在轴系发生扭振时，低压缸末级叶片等长叶片的应力变化主要取决于其振动状态，而不是叶片所处轴段承受的瞬时扭矩。根据转子-叶片耦合扭振模型可以对叶片的振动响应进行计算，从而求得叶片的实时应力。在此过程中需要首先对叶片的应力进行仿真，建立叶片应力最大处的应力与叶片上某个横截面位移之间的对应关系。

仍以该机组低压缸末级带冠叶片作为研究对象，对其进行仿真计算。由图4和图5可以看出，距离叶片根部483 mm处的截面(位置A)和叶片顶端(位置B)作为第二阶周向振动振型的2个极值点，可以以此作为扭振作用下叶片振动的观察点。其中位置A由于可以较好地反映叶片根部附近的变形，可作为叶片应力最大处的位移-应力关系曲线的参考点。

利用Ansys软件对叶轮进行自由振动响应仿真，设叶轮转速为3 000 r/min，在叶轮平均半径处(1 473.2 mm)的截面上均匀施加大小为2×105N·m的扭矩，并在1 s时停止施加扭矩，使叶片进行自由振动。位置A和位置B相对叶片根部的位移响应计算结果见图14和图15。在叶片振动过程中，叶片危险点即应力变化最大处出现在图16中箭头所示的位置，其应力历程如图17所示。

图14 位置A相对周向的位移响应

图15 位置B相对周向的位移响应

图16 应力变化最大处位置示意图

将位置A的位移与叶片应力变化最大处的应力进行对比，可以得到叶片位移-应力关系，如图18所示。由图18可以看出，位置A的位移与叶片根部的应力具有较好的线性关系。

根据叶片位移-应力关系，即可利用位置A的位移对叶片根部应力进行计算，叶片实际应力与利用叶片位移计算出的应力对比如图19所示。

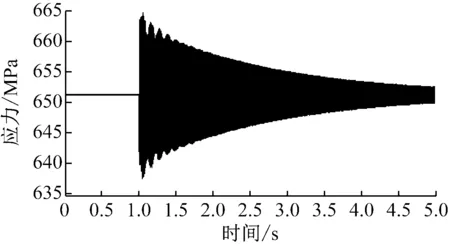
图17 叶片危险点应力历程

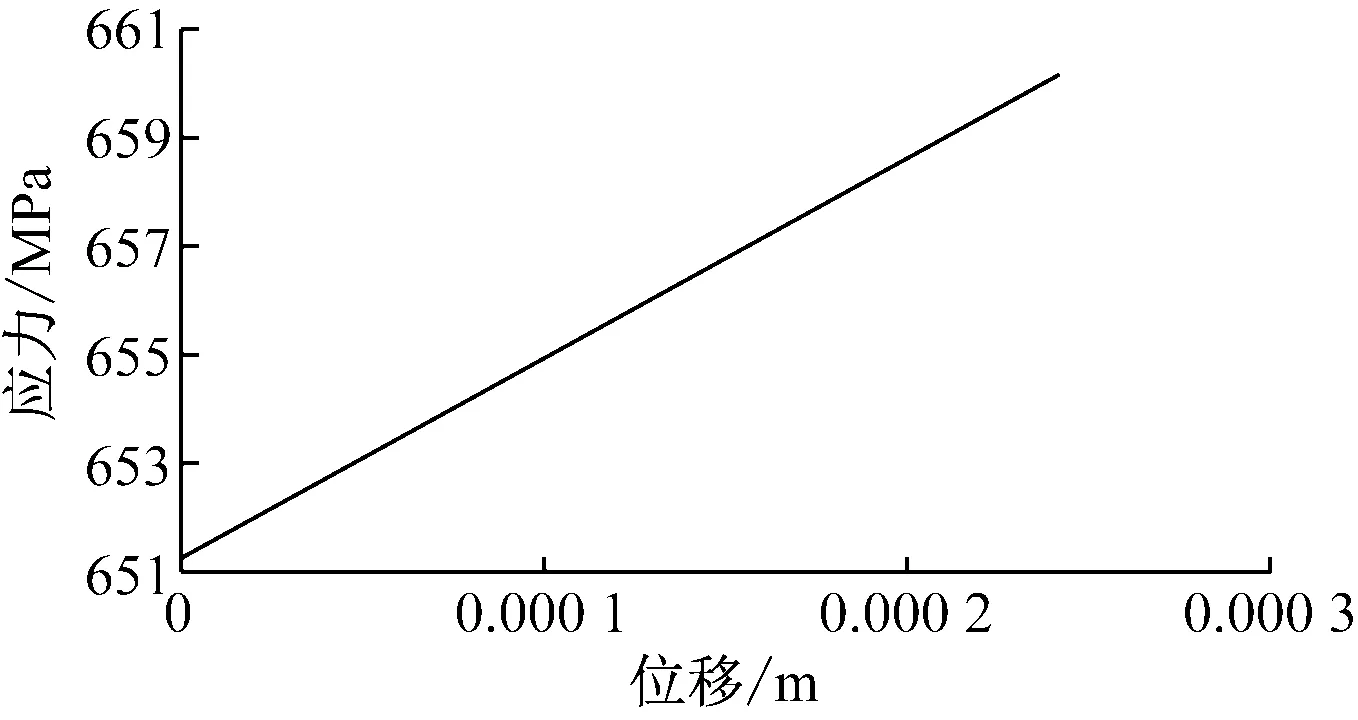
图18 叶片位移-应力关系曲线

图19 由叶片位移计算所得叶片危险点的应力

由图19可知，利用叶片的周向位移可以较为准确地计算出叶片危险点的应力。因此，只要建立起叶轮模型，使之能够准确计算轴系发生扭振时叶片的周向振动幅值，便可以计算出叶片危险点的应力历程，从而对扭振故障下叶片的疲劳寿命损耗进行评价。

5 结 论

(1)建立了转子-叶片耦合扭振模型，在该模型的基础上采用Riccati传递矩阵法和Newmark-β法相结合的方法得到转子-叶片耦合扭振动态响应，为转子和叶片的扭振疲劳寿命损耗在线分析和安全性评估奠定基础。

(2)利用叶片应力变化最大处的应力与其振动状态之间的关系，可根据转子-叶片耦合扭振模型计算得到轴系各扭振危险截面的应力历程。

[1] 晏水平，黄树红，韩守木.汽轮发电机组轴系扭振引起的叶片响应计算[J].动力工程，2001，21(4):1288-1291.

YAN Shuiping，HUANG Shuhong，HAN Shoumu. Response calculation of blade subjected to shaft torsional vibration in turbine-generator sets[J].PowerEngineering， 2001，21(4):1288-1291.

[2] 吕方明，危奇，鲁录义.汽轮机长叶片弯曲与轴系扭转耦合振动研究[J].动力工程学报，2014，34(6):443-449.

LÜ Fangming,WEI Qi,LU Luyi.Study on coupled vibration between long-blade bending and shafting torsion of steam turbine[J].JournalofChineseSocietyofPowerEngineering，2014,34(6):443-449.

[3] 闻邦椿，顾家柳，夏松波，等.高等转子动力学—理论、技术与应用[M].北京：机械工业出版社，1999.