一种测量大气消光系数边界值的新方法∗
2018-03-27孙国栋秦来安张巳龙何枫谭逢富靖旭侯再红
孙国栋 秦来安 张巳龙 何枫 谭逢富 靖旭 侯再红
1)(中国科学院安徽光学精密机械研究所,中国科学院大气光学重点实验室,合肥 230031)
2)(中国科学技术大学研究生院,合肥 230026)
(2017年9月11日收到;2017年12月4日收到修改稿)
1 引 言
大气气溶胶是指由悬浮分布在大气中的空气动力学直径在0.001—100µm之间的液体或固体颗粒物组成的稳定体系.作为大气的重要组成部分,气溶胶能通过散射和吸收太阳辐射参与云的形成,直接或间接地影响地球气候变化.此外,其对能见度、交通安全和人体健康也具有重要影响[1,2].消光系数作为表征气溶胶光学特性的重要参数,是当今大气科学和环境科学等领域的一个热点研究内容.目前,激光雷达以较高的时空分辨率等优势成为一种探测大气气溶胶消光系数和后向散射系数等光学特性的重要技术手段[3,4].在使用反演算法(Klett后向积分或Fernald后向积分)确定激光雷达探测范围内消光系数的分布时首先需要确定最大有效探测距离的消光系数,即消光系数的边界值[5−9].确定消光系数边界值的常用方法是在对流层顶附近选择气溶胶含量最小的高度作为标定点,假设该点气溶胶的散射比为某一很小的定值[10].但对于有效探测距离达不到对流层顶的低空探测激光雷达而言,这种方法就会失效.为解决该问题,国内外学者相继提出了一些迭代和估算的方法.Kovalev[11]提出了一种迭代算法,该算法利用大气气溶胶和大气分子的消光系数定义一个信号校正因子,通过迭代对信号进行校正得到大气气溶胶消光系数边界值.但是该方法校正因子的修正量不易控制,并且迭代次数较多.王治华等[12]在处理有云层的激光雷达回波信号时,将激光雷达信号在大气中的传输过程分为云层区和非云层区,忽略回波信号中的云层区信息,利用最小二乘法对非云层区的激光雷达回波信号进行拟合得到大气消光系数的边界值.但是该方法忽略了真实大气是非均匀分布的,导致计算结果出现一定的偏差.陈涛等[13]提出了一种散射比迭代法,该方法在探测范围内寻找到一个气溶胶含量相对较小的高度层,建立回波信号与边界值之间的等式关系,利用穷举法获得该高度处的气溶胶散射比并以此来确定边界值,获得了较为准确的反演结果.但是该方法是等步长迭代,要获取一个合适的气溶胶散射比需要较多的迭代次数,计算量大.
本文提出了基于Broyden算法[14]确定大气消光系数边界值的新方法,把确定大气消光系数边界值的问题转化为求非线性方程数值解的问题.根据大气消光系数边界值与激光雷达回波信号之间的关系构建了一个非线性方程,采用Broyden算法求解该方程的数值解得到大气消光系数边界值.这种方法具有迭代次数少,对初始解依赖程度小的优点.由于这种方法使用的是沿传输路径积分的雷达信号,所以适用于真实大气非均匀的情况.文中使用自行研制的成像激光雷达对提出的新方法进行了验证,并将直接测量得到的大气透过率与成像激光雷达最后获取的大气透过率进行了对比研究.
2 理论和方法
选用Klett方法[5]反演大气消光系数时首先需要确定消光系数边界值.Klett假设大气后向散射系数β和消光系数σ之间存在乘幂关系,即[5,6]

其中B0是常数,k与激光雷达波长和观测的气溶胶性质有关,按照其范围设定为常用数值1.因此单次散射激光雷达方程可以表示为[15]
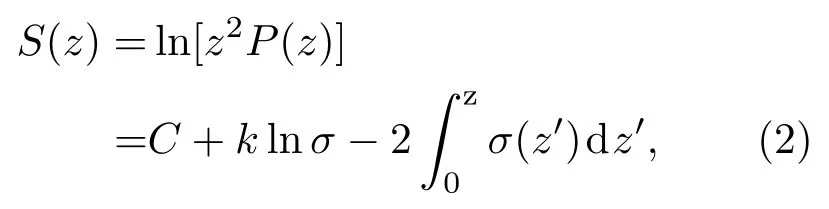
其中P(z)为从距离z处接收到的散射信号强度,C为系统常数,S(z)为距离平方矫正信号.
方程(2)的稳定解为
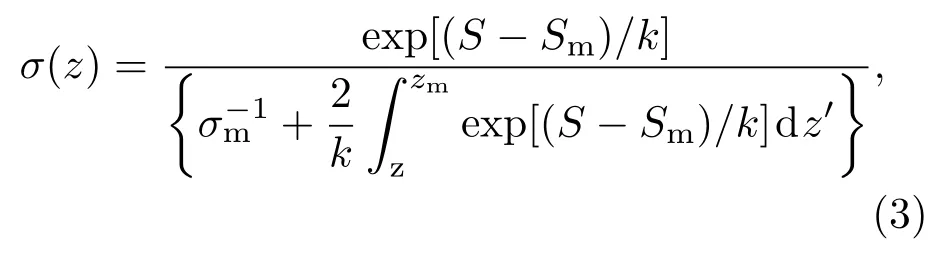
其中zm为最大探测距离,Sm为zm处的距离平方矫正信号(Sm=S(zm)),σm为zm处的消光系数(σm=σ(zm)).从方程(3)中可以看出,消光系数既与相对信号S−Sm有关,也和消光系数边界值σm相关.
利用方程(2)可以得到
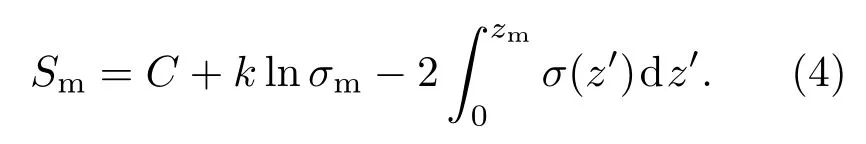
消光系数从最小探测距离到最大探测距离的积分可以表示为消光系数边界值的函数:
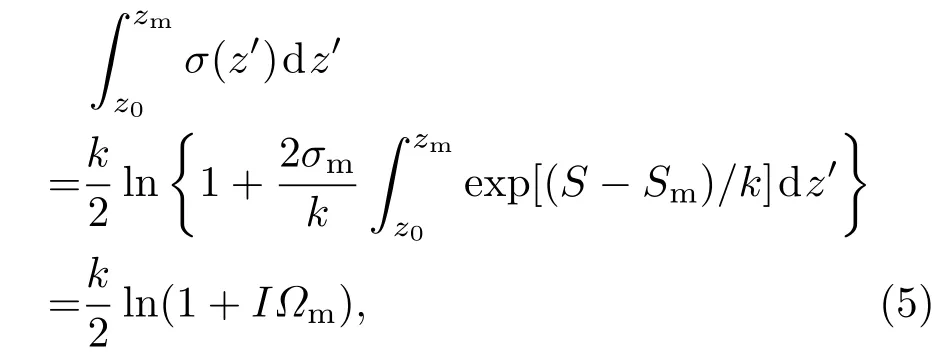
其中z0表示初始距离,
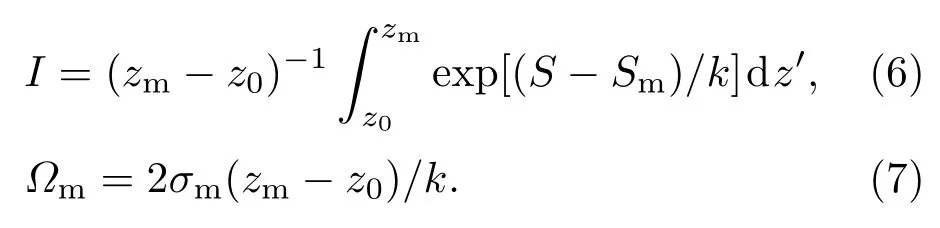
由方程(5)可知消光系数的平均值主要依赖于信号积分I的幅度.确定消光系数边界值的常用方法是把消光系数边界值设定为与平均消光系数相等来解不等式方程.即
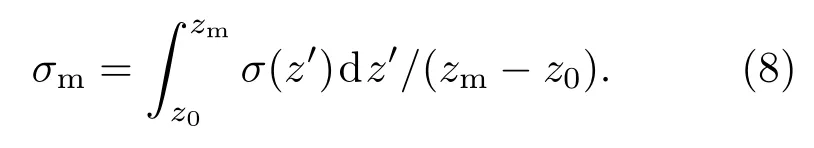
由方程(5),(7)和(8)可以得到以下方程:
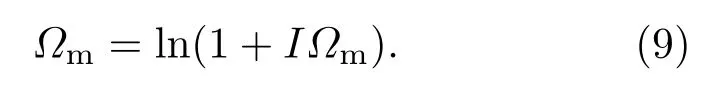
将方程(7)代入方程(9)中,令σm=x,设
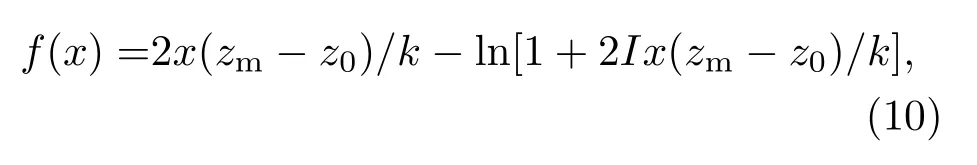
即将消光系数边界值的确定问题转化为非线性方程数值解的求解问题.求解非线性方程最常用的方法是牛顿法[16].它具有简单的迭代形式和二次收敛速度.对于充分接近解的初值,该方法会迅速收敛到精确解.但由于每次迭代都需要计算导数,导致该方法运算量较大.本文中需要求解的方程(10)本身较为复杂,因此其导数难以求解,此时牛顿法就不再适用.为了解决这个问题,目前已经提出了很多技术手段,其中最成功的一类为拟牛顿法[17].拟牛顿法利用函数值逼近导数值,从而避免了导数的计算.函数在任意点xr处的一组导数值可以写成雅可比矩阵的形式:
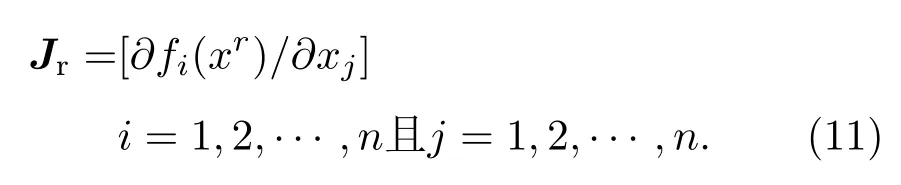
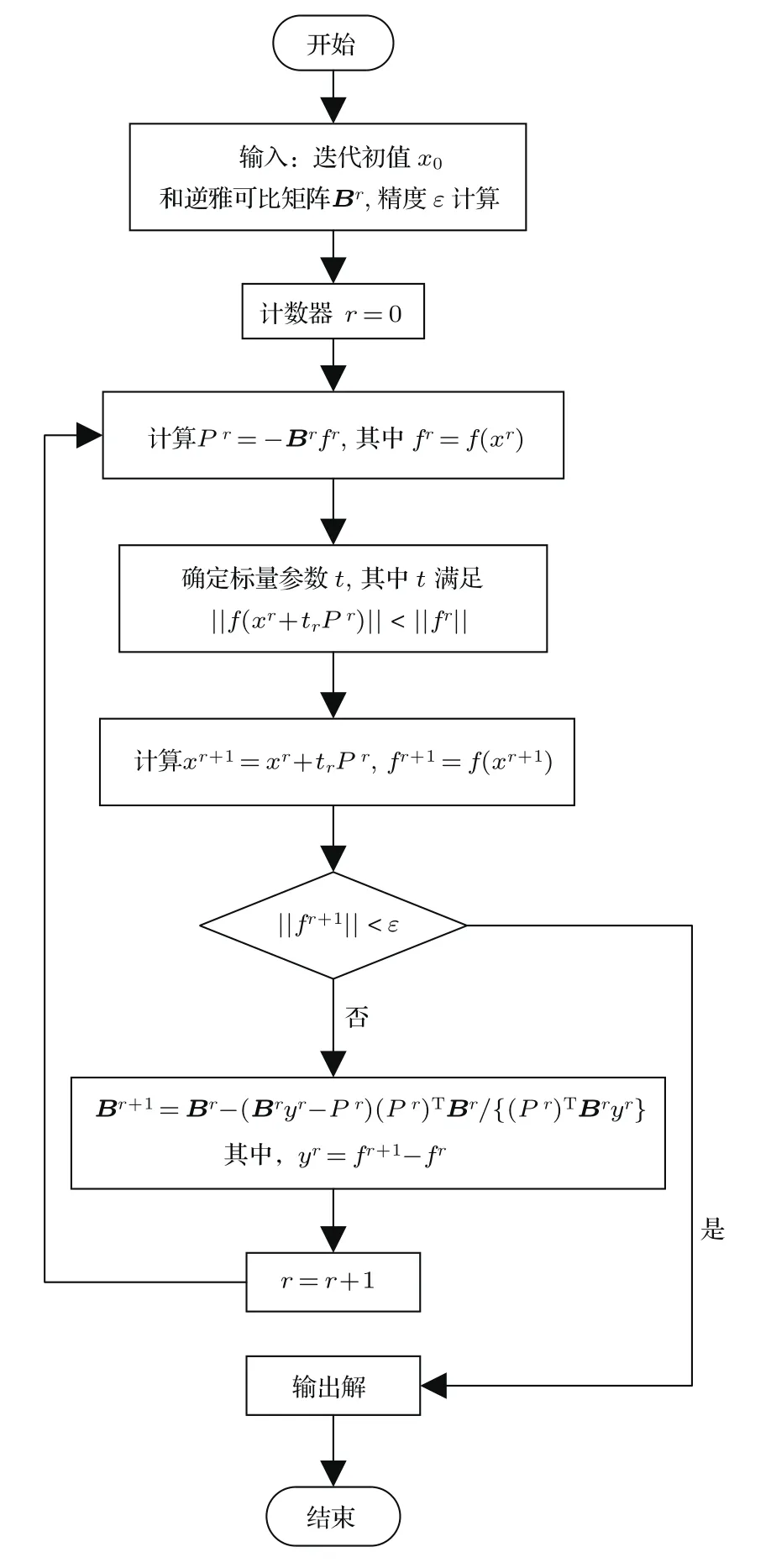
图1 Broyden算法流程图Fig.1.The flow chart of Broyden algorithm.
拟牛顿法提供了一个更新公式,对每次迭代该公式给出了雅可比矩阵的连续逼近,Broyden等已经证明,在特定情况下该更新公式对逆雅可比矩阵也提供了满意的近似.Broyden算法作为拟牛顿法的一种具体形式,它的算法结构如下[14]:
1)输入解的初始近似,设置计数器r为零;
2)计算或假设逆雅可比矩阵Br的初始近似;
3)计算Pr=−Brfr,其中fr=f(xr);
4)确定标量参数t,使其满足‖f(xr+trPr)‖<‖fr‖,其中符号‖∗‖表示待取向量的模;
5)计算xr+1=xr+trPr;
6)计算fr+1=f(xr+1),如果‖fr+1‖<ε(其中,ε是一个很小的预先设定的正数),则退出;否则执行第7步;
7)利用更新公式得到雅可比矩阵的近似
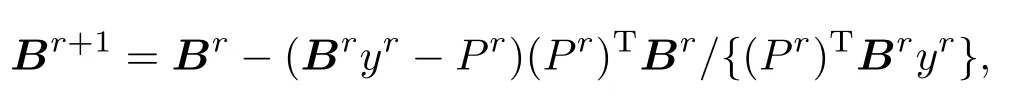
其中yr=fr+1−fr;
8)令r=r+1,返回到第3步.
上述算法的结构流程如图1所示.
3 实验与系统
3.1 成像激光雷达系统
成像激光雷达系统主要由激光器、望远镜、电荷耦合器(CCD)、滤光片和数据采集与控制系统组成,其结构和性能在文献[18]中有详细说明.成像激光雷达系统的实验测量原理如图2所示,其中,D为收发间距,dθ为像元对应的张角,γ为CCD倾角.该系统的工作原理可以简述为:激光器向大气中发射一束激光,由于激光与大气发生相互作用产生散射光,散射光中包含了大气分子和气溶胶的信息,CCD相机中的像元记录了光束上各散射高度的散射光子数,即回波信号强度.

图2 成像激光雷达系统Fig.2.System of imaging lidar.
3.2 图像数据处理过程
为获得随高度变化的回波信号,需对存储的图像文件进行处理[18−20].处理步骤如图3所示.经过处理得到的回波信号强度个例如图4所示.然后将各个位置处的回波信号强度以及其他的参数值代入非线性方程(10)中,运用Broyden算法对消光系数边界值进行求解.由于得到的消光系数边界值的准确性无法定量给出,需要将其转化为可以对比研究的量.本文利用求得的消光系数边界值进一步求解得到消光系数的路径分布,然后按照路径积分获得探测范围内的大气透过率,以大气透过率作为一个对比量.
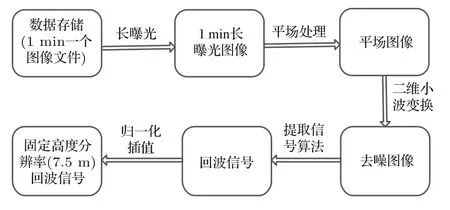
图3 图像处理过程Fig.3.The procedure of image processing.
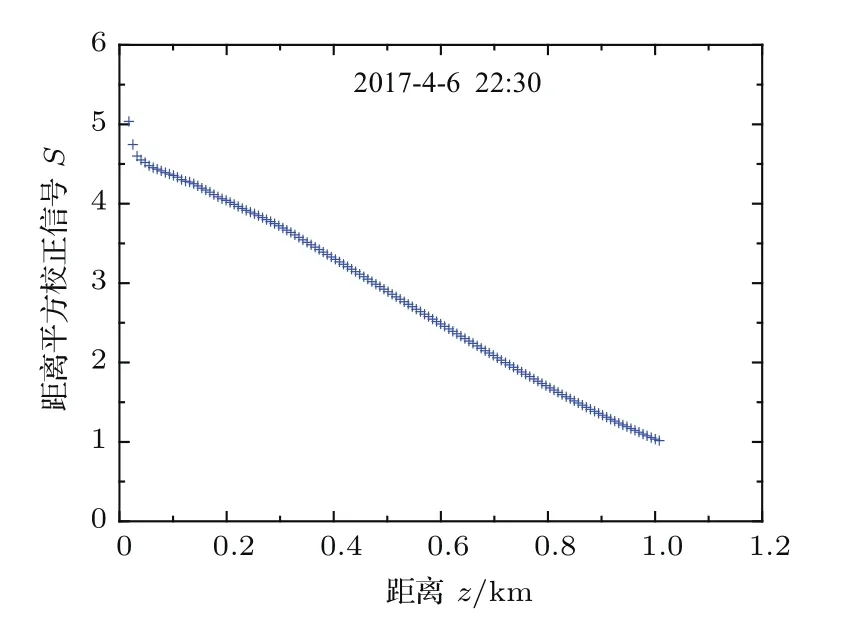
图4 回波信号强度个例Fig.4.Example of return signal.
3.3 对比实验系统
本文将没有经过反演算法计算的直接测量的大气透过率作为对比实验,如图5所示.直接大气透过率测量装置分为发射装置和接收装置.实验时,发射装置将出射光分成功率相等的两束激光,一束光用于监测出射功率,另外一束光到达接收装置.接收装置测量传输到接收端的激光束能量,通过与发射端的监测光束能量对比,获得大气透过率.

图5 1 km实验地点地图Fig.5.Experimental site map of 1 km.
4 结果与分析
4.1 两种确定消光系数边界值方法的对比
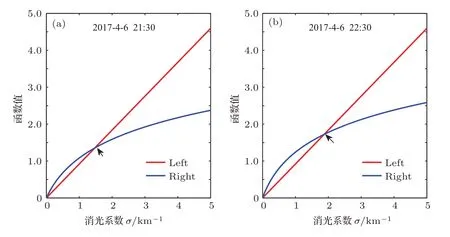
图6 Broyden方法的初值 (a)21:30;(b)22:30Fig.6.Initial value of the Broyden algorithm:(a)21:30;(b)22:30.
利用Broyden方法求解非线性方程确定消光系数边界值时首先需要给定初始值,初始值选定的精确与否也决定了其迭代次数.同时也需要给定迭代的容差,本文中设定为10−6.初始值的选取采用同一天的21:30和22:30两个时间点获取的信号来说明,如图6所示.其中left表示以等式(9)左边的项绘出的曲线,right表示以等式(9)右边的项绘出的曲线,图6(a)和图6(b)中的left和right均有交点,该交点就是非线性方程(10)的数值解.从图中可以得到该数值解的大致位置,即Broyden算法的初始值.选取不同的初始值得到最后的结果需要不同的迭代次数,如表1所列.选取的初值越接近方程的解其对应的迭代次数就会越少,但是只要选择的初值在合理的范围内,最后由Broyden算法都能得到最终解且大小相等.这充分说明采用Broyden算法对上述非线性方程式的求解是有效的.
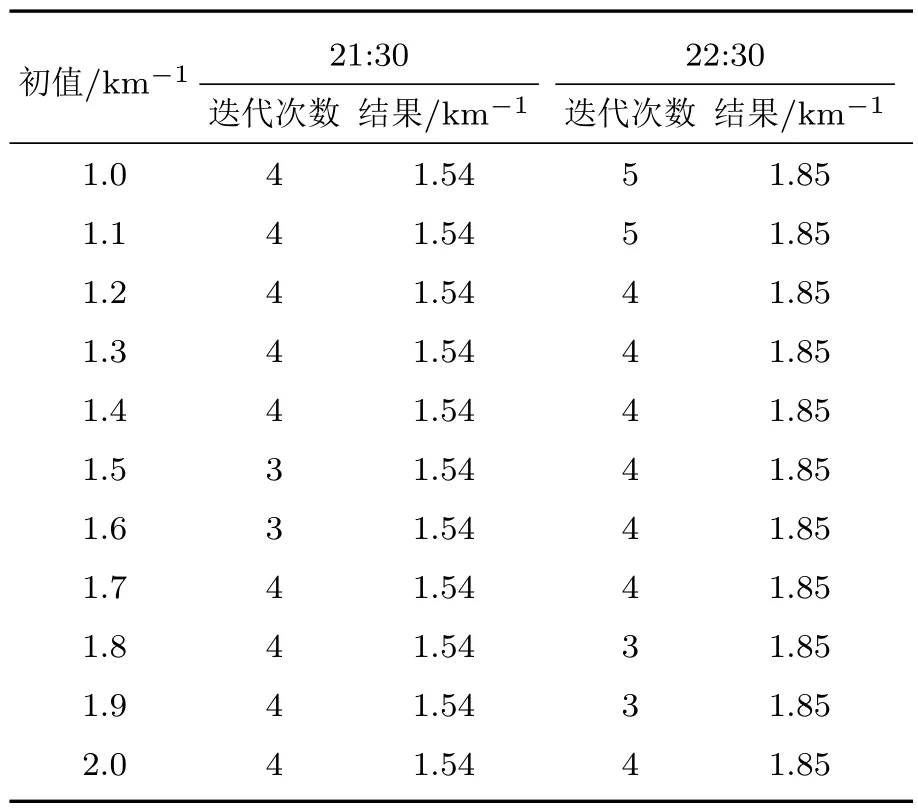
表1 选择不同初值的迭代结果Table 1.Iterative results with different initial values.
本文运用Broyden算法和最小二乘法分别求取实验期间内大气消光系数的边界值,如图7所示.两种方法测量得到的边界值在趋势上是一致的,但是在整个测量时间段的前期和后期均具有一定的差异,尤其是在边界值较大的情况下两种方法的实验结果差异较大,最小二乘法大于Broyden算法求取的边界值.
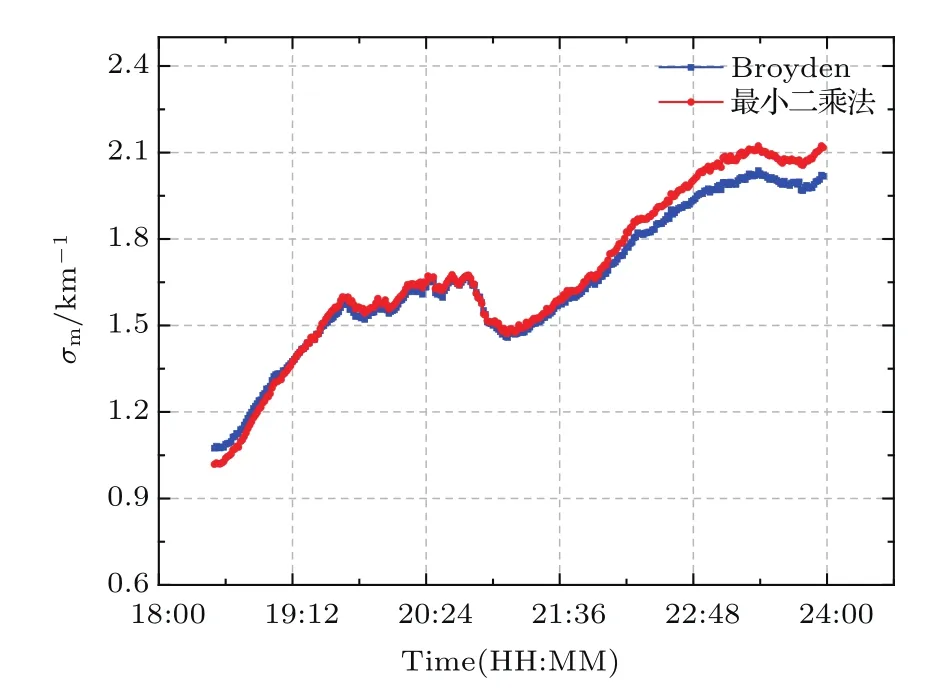
图7 两种方法测量的边界值对比Fig.7.Comparison of boundary values measured by two methods.
4.2 不同方法下获得的大气透过率对比结果
通过上述方法获得了消光系数边界值之后,利用激光雷达方程的稳定解(3)式可以得到探测范围内消光系数的分布.本文分别以21:30和22:30两个时间点为例,利用两种方法测量得到1 km以内的消光系数的水平空间分布,实验结果如图8所示.
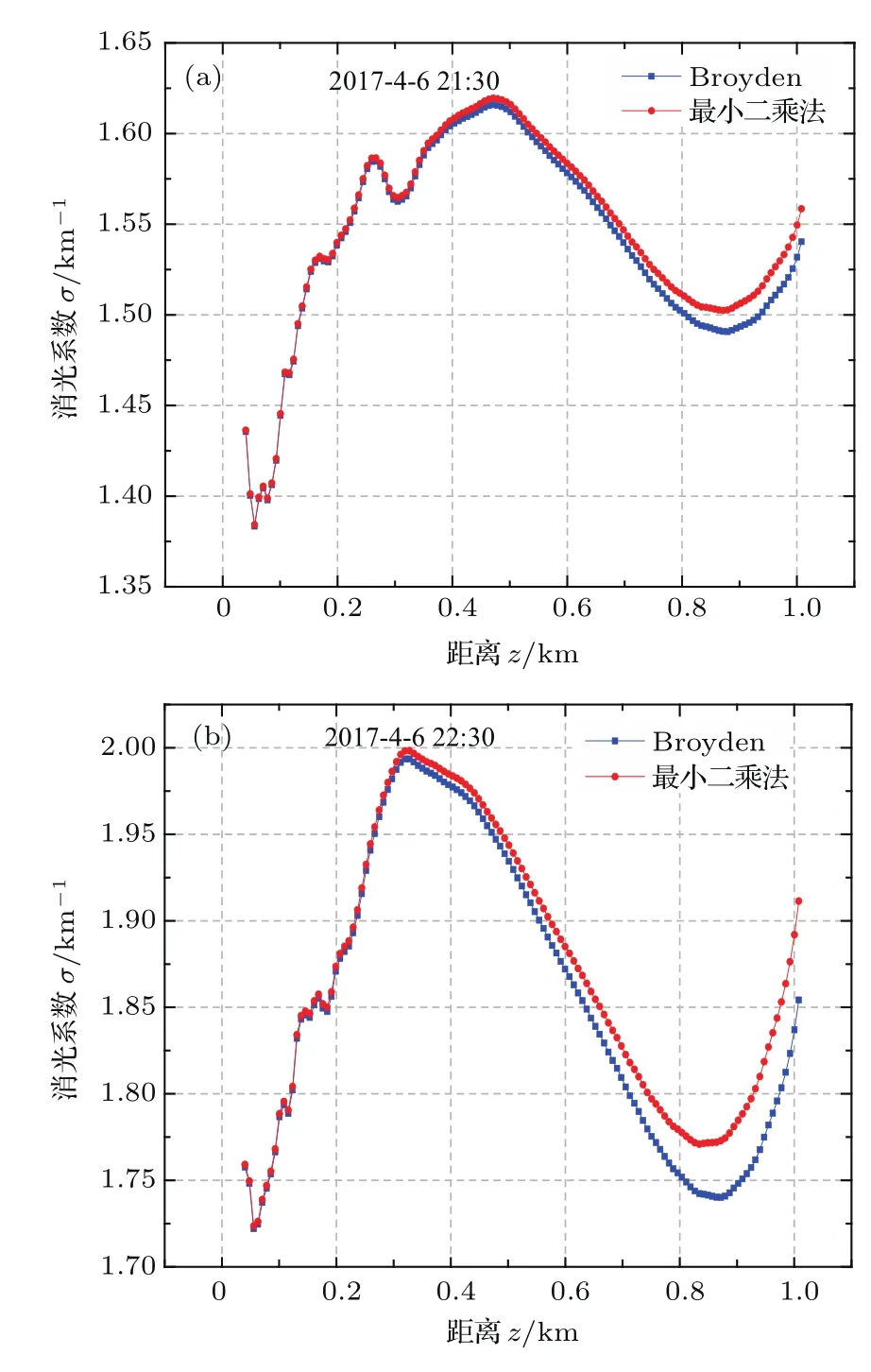
图8 水平消光系数分布 (a)21:30;(b)22:30Fig.8. Distribution of horizontal extinction coeffi-cients:(a)21:30;(b)22:30.
图8表明消光系数的水平分布是不均匀的,因为实验场地并不单一,激光光束经过的范围内有草地、水库、马路等.对探测时间段内所有的数据进行反演计算得到了其随时间和水平空间变化的消光系数分布.由于求得的消光系数边界值的不同,造成了两种方法测量得到的水平消光系数也有一定的差异.
用两种方法测量得到的消光系数分布依据大气透过率计算(12)式可以计算得到1 km范围内的大气透过率T随时间变化的情况:
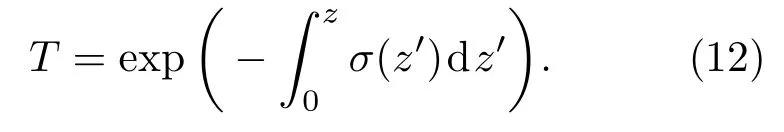
将这两种方法与直接大气透过率测量装置(3.3节)测得的大气透过率进行对比,结果见图9.Direct,Old,New分别表示直接进行测量、利用最小二乘法测量以及本文提出的Broyden算法测量的大气透过率.从对比图像来看,Broyden算法与直接大气透过率测量结果趋于一致,而利用最小二乘法得到的测量结果偏小.将直接大气透过率测量结果作为横轴,最小二乘法和Broyden算法测量的大气透过率数值作为纵轴进行相关性分析,结果如图10所示,两种处理算法与直接测量结果之间的相关系数分别为0.958和0.968.本文提出的方法测量的结果与直接大气透过率的测量结果更为一致.
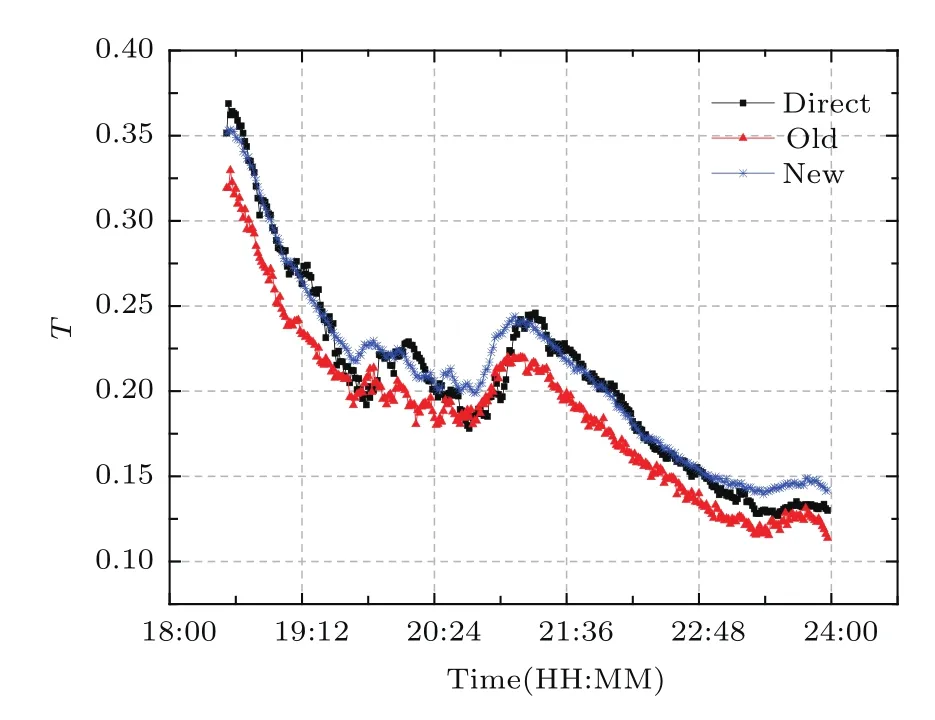
图9 不同方法下测量的水平大气透过率Fig.9.Horizontal transmittance measured by different methods.
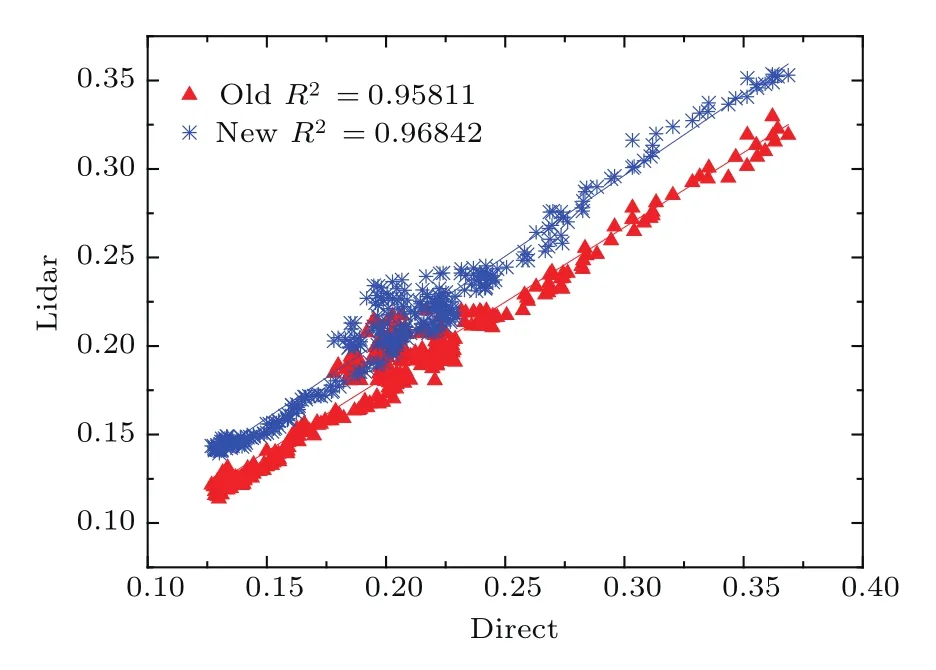
图10 激光雷达反演大气透过率结果直接测量的大气透过率之间的相关性Fig.10.The correlation between the transmittance inverted by lidar and direct transmittance results.
4.3 相对误差分析
为了更进一步说明两种方法的差距,以直接测量得到的大气透过率作为参考标准,将两种反演方法得到的大气透过率与参考标准之间进行相对误差分析,如图11,蓝线是测量时间段内所有的相对误差,红线是界限误差,黑线是平均误差,两种反演方法与参考标准之间的相对误差均在20%之内.以相对误差值为7.5%作为界限误差,Broyden算法得到的大气透过率与参考标准之间的相对误差在7.5%以上的数据占总数据的24%,平均相对误差为4.66%;最小二乘法得到的大气透过率与参考标准之间的相对误差在7.5%以上的数据占总数据的70%,平均相对误差为9.10%.充分说明了利用本文提出的方法进行测量的结果具有一定的优势.
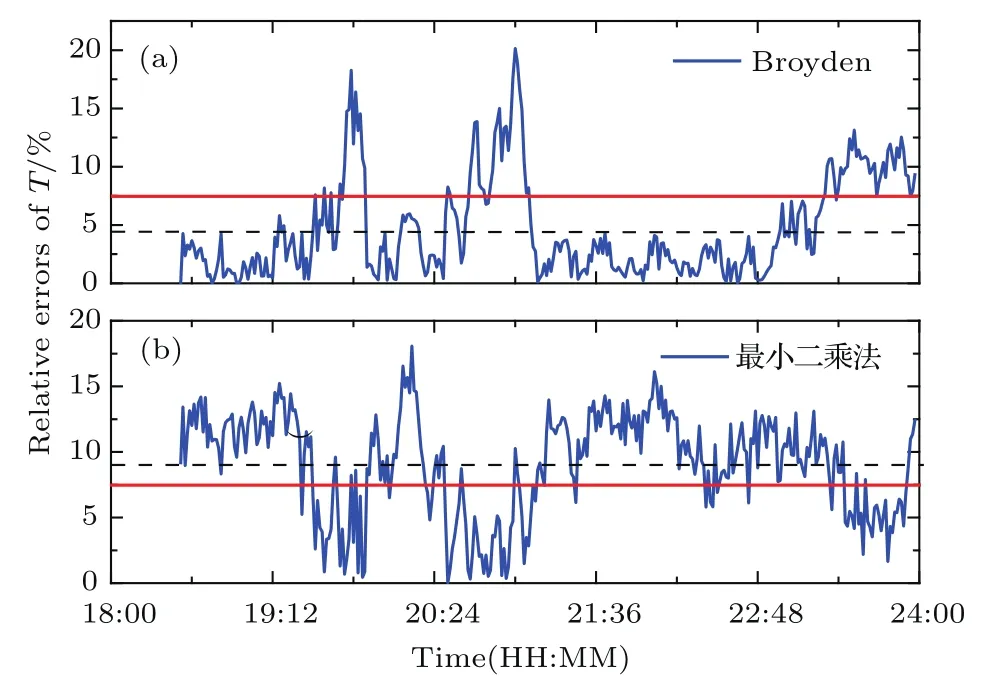
图11 不同反演方法与直接测量得到的透过率之间的相对误差 (a)Broyden方法与直接方法;(b)最小二乘法与直接方法Fig.11.Relative errors of transmittance between different inverse method and direct method:(a)Broyden method and direct method;(b)least square method and direct method.
5 结 论
当牛顿法不适用于求解激光雷达反演过程中的非线性方程时,Broyden算法可以作为一种恰当的方法来完成这一计算.对于初值的选取只要是在合理的范围之内,都能通过有限的迭代次数获得一致且较为准确的解,即消光系数边界值.当然选取的初值越接近真实解迭代速度就会越快.通过对比最小二乘法和本文提出的算法计算得到的大气透过率,结果表明消光系数边界值求取的准确性对于最后大气透过率结果的准确性有明显影响,并且通过与直接测量得到的大气透过率之间的相关性和相对误差分析,进一步验证了本文提出的算法相比于最小二乘法有一定的优势.因此本文提出的利用Broyden算法确定消光系数边界值的方法是有效的.目前本文中处理的激光雷达数据只考虑了单次散射而未考虑多次散射的影响,因此在以后的工作中将进一步加入多次散射的相应分析.
[1]Man S W,Kai Q,Hong L,James R C,Kwon H L 2017Atmos.Environ.154 189
[2]Zhao G Y,Liang M,Li Y Y,Duan Z,Zhu S M,Liang M,Sune S 2017Appl.Opt.56 1506
[3]John E B,Sebastian B,Robert B,Parikh N C 2003Appl.Opt.42 2647
[4]Liang M,Mikkel B 2015Opt.Express23 A1613
[5]James D K 1985Appl.Opt.24 1638
[6]James D K 1981Appl.Opt.20 211
[7]Liang M,Peng G,Yang Y,Zheng K 2017Opt.Express25 A628
[8]Cao N W 2015Optik126 2053
[9]Masap M,Nobuo T 1994Appl.Opt.33 6451
[10]Zhou J,Yue G M,Qi F D 1998Chin.J.Quant.Elect.15 140(in Chinese)[周军,岳古明,戚福第1998量子电子学报15 140]
[11]Kovalev V A 1993Appl.Opt.32 6053
[12]Wang Z H,Wang H B,He J,Zheng Y C,Yang J G,Li Y Q,Zhao X B 2008Laser J.29 36(in Chinese)[王治华,王宏波,何捷,郑玉臣,杨经国,李跃清,赵兴炳2008激光杂志29 36]
[13]Chen T,Wu D C,Liu B,Cao K F,Wang Z Z,Bo G Y,Yuan L,Zhou J 2010Acta Opt.Sin.30 1531(in Chinese)[陈涛,吴德成,刘博,曹开法,王珍珠,伯广宇,袁林,周军2010光学学报30 1531]
[14]George L,John P(translated by Li J,Ren M M)2016Numerical Methods Using MATLAB(Beijing:China Machine Press)pp116–117(in Chinese)[乔治 L, 约翰P著(李君,任明明译)2016数值方法-MATLAB版(北京:机械工业出版社)第116—117页]
[15]Ma X M,Tao Z M,Ma M J,Li C J,Wang Z Z,Liu D,Xie C B,Wang Y J 2014Acta Opt.Sin.34 0201001(in Chinese)[麻晓敏,陶宗明,马明俊,李成军,王珍珠,刘东,谢晨波,王英俭2014光学学报34 0201001]
[16]Anne G,Timothy P C(translated by Wu Z J,Wang G Y,Fan H J)2016Numerical Methods(Beijing:China Machine Press)p63(in Chinese)[安妮 G,蒂莫西 P C著(吴兆金,王国英,范红军译)2016数值方法(北京:机械工业出版社)第63页]
[17]Xiong X L,Jiang L H,Feng S,Zhuang Z B,Zhao J Y 2012Infrar.Laser Eng.41 1744(in Chinese)[熊兴隆,蒋立辉,冯帅,庄子波,赵俊媛 2012红外与激光工程 41 1744]
[18]Sun G D,Qin L A,Cheng Z,Hou Z H 2017Laser Optoelect.Prog.54 090102(in Chinese)[孙国栋,秦来安,程知,侯再红2017激光与光电子学进展54 090102]
[19]Yang C P 2011M.S.Dissertation(Dalian:Dalian Maritime University)(in Chinese)[杨成鹏 2011硕士学位论文(大连:大连海事大学)]
[20]John E B,Parikh S,Trevor B K 2007Appl.Opt.46 2922
