平凸透镜焦距的测量与研究

陈 舟 倪 敏

(上海师范大学数理学院 上海 200234)

1 引言

厚透镜与薄透镜不同，测量焦距时起始点不在透镜中央，也不在边缘.在大学物理实验中，常利用光具座和测节仪等测量厚透镜的主点、焦点等[1].我们主要利用学生已经学习过的知识，利用球面折射的基本公式和透镜成像法，测量出光线会聚点与透镜边缘的距离[2]，结合基点、基面的知识，得到透镜焦距；也可以通过入射角、折射角计算透镜折射率[3]，用游标卡尺测量透镜长度、厚度，利用勾股定理得到透镜的曲率半径，代入厚透镜的焦距测量公式计算得到焦距，从而对透镜成像法所得结果进行检验，确定焦距的值以及测量的始末点.两种方法各有优劣，透镜成像法的优势在于免去测量透镜的曲率半径，以防透镜外形不规则，曲率半径用勾股定理难以测量；由于在测量中要求近轴光线，因此焦距公式法可避免在焦距的测量中光线偏离光轴的问题.但两种方法均能简化实验方法，帮助学生理解光学元件的3对基点，符合学生的认知能力和水平，巩固对于光学知识的掌握，通过实验对公式进行验证，逐步培养学生理论联系实际的能力以及实事求是的科学态度.

2 实验原理

2.1 基本参量

透镜两表面在其主轴上的间隔称为透镜的厚度.若透镜的厚度与球面的曲率半径相比不能忽略，则称为厚透镜；若可略去不计，则称为薄透镜.对于厚透镜而言，它有6个基点，分别为主点、节点和焦点，它们又有物方和像方之分.

(1)焦点

平行于主轴的入射光线折射后和主轴相交的位置称为像方焦点F′.如果把物点放在主轴上某一点时，发出的光折射后将产生平行于主轴的平行光束，那么这一物点所在的点称为物方焦点F.过F垂直于主轴的平面称为物方焦面，过F′垂直于主轴的平面称为像方焦面.

(2)主点

将物体垂直于光轴放置在主轴上的某点，在另一处会形成等大正立的像，主轴上的这两个点，分别称为物方主点H和像方主点H′.即物方主点是物空间中横向放大率为+1β=+1的垂轴平面与主光

轴的交点，像方主点是物方主点关于透镜的共轭点.过物方主点和像方主点垂直于光轴的两个平面分别称为物方主平面和像方主平面.

(3)节点

节点是透镜主轴上角放大率γ=+1的两个共轭点.入射光线(或延长线)通过物方节点时，出射光线(或延长线)必通过像方节点，并与入射光线平行.过物方节点和像方节点垂直于光轴的平面分别称为物方节面和像方节面.

当厚透镜两侧处于同一介质即折射率相同时，主点与节点位置重合[4].

2.2 球面折射原理

当光线从空气中射入折射率为n,半径为r1的球面介质中时，如图1所示，在近轴光线的条件下，由近轴光线下球面折射的物像公式可得

图1 光线从空气中射入球面介质

当s1=-∞时，即光线平行于主轴入射，得到像方焦距

同理，当光线从折射率为n,半径为r2的凹球面介质进入空气中发生折射时可得

当s2=-∞时，即光线平行于主轴入射，得到像方焦距

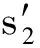
2.3 厚透镜聚光原理

厚透镜结构如图2所示.

对折射球面O1

对折射球面O2

图2 厚透镜的基点和基面

因为

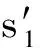
且

可得

(1)

由透镜高斯公式

假定物距和像距的参考原点从O1和O2分别移动了距离p和p′，则

(2)

比较式(1)和式(2)，计算得到

所以，对于厚透镜而言，如果令

则空气中厚透镜的物像公式的高斯形式与薄透镜的相同，皆为

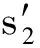
2.4 平凸透镜聚光原理

平凸透镜相当于一边曲率半径为无穷大的厚透镜，因此在计算主点和焦距时可将r1或r2取为无穷大[7].

(1)左凸右平(r2=∞)(图3)

图3 左凸右平

则

所以

(2)左平右凸(r1=∞)(图4)

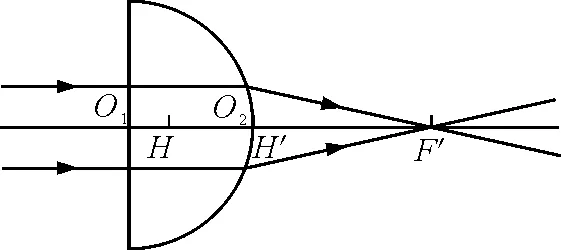
图4 左平右凸

则

所以

通过计算可以看出，平凸透镜在左平右凸和左凸右平两种情况下，透镜焦距是相同的，而测量焦距的起始位置不同.由计算可知p和p′的大小取决于透镜厚度以及透镜折射率.

3 实验内容和实验方法

3.1 焦距公式法测平凸透镜焦距

(1)测量透镜曲率半径

由于平凸透镜为圆柱体的一部分，因此设此圆柱体的半径为r，透镜平面的长度为d，透镜的厚度为h，如图5所示，其中平凸透镜为黑色边框加粗的部分.根据勾股定理可知

即

用游标卡尺测量平凸透镜平面的长度d和透镜厚度h，测量3组求出平均值，计算平凸透镜的曲率半径.

图5 平凸透镜几何图

(2)测量透镜折射率

将透镜放在刻度盘上，调整入射光线的角度，使光线从透镜直边进入，观察折射光线.由于折射光线从曲边出射时会再次发生折射，因此不能直接测量出射光线.测量时需要记录出射光线与透镜曲边的交点，连接入射点与交点，并将其延长，与刻度盘的边缘相交，即可得到折射角的大小.原理图如图6所示.

n1sini1=n2sini2

由于透镜在空气中，因此

重复测量3次求平均值.

图6 折射原理图

(3)利用折射球面的像方焦距公式计算透镜焦距

将测得的透镜曲率半径及折射率代入折射球面的焦距公式式(3)和式(4)，计算出平凸透镜两个方向上的焦距即物方和像方空间的焦距.

3.2 透镜成像法测平凸透镜焦距

(1)同3.1中(1)用游标卡尺测量透镜的厚度h.

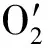
(3)平行光照射平凸透镜的曲边(左凸右平)，如图7所示，画出光的传播路径，记录光线的会聚点，测量直边到交点的距离O2F′，由于透镜基点H′与O2不重合，得到

负号表示H′在O2左侧，因此

则

重复测量3次求透镜焦距平均值.

图7 平行光照射平凸透镜曲边

(4)平行光照射平凸透镜的直边(左平右凸)，将平凸透镜翻转，如图8所示，重复上述步骤(3)，由于p′=0即H′与O2重合，测量出曲边到交点之间的距离O2F′，即为焦距f′，则

f′=|O2F′|=|H′F′|

重复3次求透镜焦距平均值.

图8 平行光照射平凸透镜直边

(5)将透镜焦距的成像法与公式法比较，求其相对误差η.

4 实验结果分析

根据实验要求,由透镜成像法和厚透镜的焦距公式测得平凸透镜焦距f′(包括左凸右平以及左平右凸两个)，并将成像法所得的数据与公式法比较，以公式法所得结果为理论值，计算相对误差，实验结果如表1和表2所示.

表1 左凸右平透镜的实验数据

表2 左平右凸透镜的实验数据

通过采用尽可能简单的实验仪器，结合基点、基面及厚透镜成像等实验原理，对平凸透镜的参数进行测量，优化了实验方法，由测量数据可见：以成像法测得的透镜焦距与测量相关参数代入厚透镜的焦距公式进行计算而得的数据基本吻合，误差小于3%.透镜成像法是利用凸透镜会聚光线的原理，测量平行光线通过透镜后会聚点与透镜边缘的距离，考虑到基点、基面，加上基点到透镜边缘的距离，两者之和即为透镜的焦距.由于公式的推导中要求近轴光线，因此平行光必须尽可能靠近轴线，减小误差.其优点在于对平凸透镜本身无过高要求.公式法是通过将相关参数代入公式计算得到平凸透镜的焦距，避开了直接测量焦距中由于光线偏离轴线带来的误差，但其同样有一定的局限性.透镜的曲率半径是通过测量透镜长度和厚度，利用勾股定理计算得到的，这就意味着透镜必须为从一个圆柱体上一刀切下的一块，边缘处不能有磨损或损耗，否则需要通过其他方式计算透镜曲率半径，增大了实验的难度.所以两种测量方法可根据实际需要正确选择应用.

通过成像法的测量和公式法的验证，证实了理论推导中得到的基点和基面，解释了成像法测厚透镜焦距时测量起始点是不同的，不能简单地看成透镜中央或透镜边缘，而需要根据p′的值加以判断.对于平凸透镜，左凸右平情况下

左平右凸时p′=0，即前者基点在透镜平面左侧，后者基点在透镜凸面边缘.由此可知对于一般厚透镜也是如此，基点即测量焦距时的起始点并不一定在透镜中央或透镜边缘，由3.3中的理论推导

和

此外，以公式法和成像法测量平凸透镜的焦距，其准确度较高，符合实验要求，由此也可引申出从实验角度测量出透镜焦距f,折射率n和曲率半径r中任意两个参量去求另一参量.作为设计实验，让学生自行研究平凸透镜的相关参量，增强学生的实验设计能力以及操作能力.

在实际测量中需注意以下3点：

(1)考虑到符号法则，因此左凸右平和左平右凸情况下曲面的曲率半径为一对相反数.

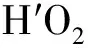
(3)当入射光线从平凸透镜的平面和曲面射入时，成像法测得的焦距大小有所不同，原因在于实际测量中，光线偏离了轴线，导致误差的产生.

5 结束语

从二期课改的角度来看，物理实验教学的地位在逐步提升，考虑到高中生的理论知识以及实验能力，这部分内容可以作为拓展实验课程教学内容，让学生自行设计实验方法进行课题研究，对基点、基面等概念有更深刻的了解，也可作进一步引申，作为测量折射率和曲率半径的另一方法.对于学有余力的学生可在本实验的基础上进行拓展，引入大学中测量相关参量的办法，丰富物理师范生对物理实验设计内容的研究，有助于培养学生创新、设计和拓展实验的思维能力.

1 林盛松，张和民.谈光组基点测定实验教学.西南师范大学学报(自然科学版)，1994，19(5)：567～570

2 翟勇.如何测量凸透镜的焦距.中学生数理化(八年级物理)(配合人教社教材)，2013(11)：16～17

3 郑永令.光的反射与折射.物理教学，2012，34(6):6～10

4 杨述武.普通物理实验(光学部分). 北京：高等教育出版社，2007.24～25

5 母国光.光学.北京：人民教育出版社，1979.40～45

6 姚启钧.光学教程.北京：高等教育出版社，1984.165～167

7 卢杰，韩力，曲延吉.用移测显微镜测量平凸透镜的基点.物理实验，2014，34(10)：8～11