动态平衡问题教学探讨*——对2017年高考全国卷Ⅰ理综第21题的分析与教学思考

陈志军

(安徽省绩溪中学 安徽 宣城 245300)

动态平衡是物体平衡类问题的一种，这类问题中物体的受力有恒力，也有动态变化的力，即力的大小和方向均发生变化，往往给解题带来困难，也是教学的一个难点.解决这类问题的一般思路是把“动”化为“静”，“ 静”中求“动”.这类问题比较多的集中在物体受到3个共点力而处于动态平衡，常常利用三力平衡的特点来讨论.2017年高考全国卷Ⅰ理综第21题就是此类典型的问题，下面对该题进行分析拓展，并对动态平衡问题的教学进行研究.

1 原题的解析

A．MN上的张力逐渐增大

B．MN上的张力先增大后减小

C．OM上的张力逐渐增大

D．OM上的张力先增大后减小

分析:本题的命题立意是考查三力动态平衡问题的求解和矢量三角形法则，要求学生有很高的利用数学知识解决物理问题的能力，对学生的要求比较高，这也要求我们在平时的教学过程中，要加强数学方法的运用，训练一题多解、举一反三，提高学生的发散性思维.

图1 题图

解析:

方法1:矢量圆法

以重物为研究对象，物体受到3个力，分别是重力mg,MN上拉力F1和OM绳上拉力F2.由题意知，3个力合力始终为零，将3个力的矢量组成如图2所示的三角形，考虑到题目要求角度α不变，即要求力F1和F2的夹角不变，结合矢量三角形图2可以看出力F1和F2的交点一定在以重力mg为弦对应的圆周上，利用矢量圆法可以看出，在F2转至水平的过程中，MN上拉力F1逐渐增大(F2转至水平水平时，F1达到最大值)，OM绳上拉力F2，先增大后减小，故选A,D.

图2 矢量圆法分析图

方法2:拉密定理或正弦定理

仍然以重物为研究对象，将重力mg,MN上拉力F1,OM绳上拉力F2，3个力组成矢量三角形，如图3所示，各力之间的夹角已标出，由正弦定理得

图3 正弦定理分析图

本题α不变，β增大，γ从钝角变化到锐角，因此sinβ增大，sinγ先增大后减小，根据上式可知MN上拉力F1逐渐增大，当β=90°时，F1达到最大值；OM绳上拉力F2先增大后减小.

2 动态平衡问题的教学方法探讨

2.1 解析法

解析法经常用于绳直接拉物体或跨过光滑滑轮拉物体，处理时要先正确分析物体的受力，画出受力分析图，假设一个角度，利用三力平衡或正交分解得到拉力的解析方程式，确定所求力与所设角度的三角函数关系，利用角度的动态变化研究三角函数的变化，可清晰得到力的变化情况.

【例1】人站在岸上，通过光滑的定滑轮用绳牵引河中的小船，如图4所示，若水的阻力不变，则船在匀速靠岸的过程中，下列说法中正确的是( )

A.绳的拉力F不断增大

B.绳的拉力F保持不变

C.船受到的浮力保持不变

D.船受到的浮力不断减小

E.小船受的合力不断增大

图4 例1题图

解析:利用解析法，对匀速运动的船受力分析，船受到重力mg，拉力F，浮力F浮和阻力f，运用正交分解，可以得到：

水平方向

Fcosθ=f

竖直方向

Fsinθ+F浮=mg

船在匀速靠岸的过程中，θ角增大，所以sinθ增大,cosθ减小，又因为重力mg和阻力f不变，因此拉力F增大，浮力F浮减小.

2.2 矢量三角形图解法

矢量三角形图解法适用于物体所受的3个力中，有一个力的大小、方向均不变(通常为重力)，另一个力的方向不变，大小变化，而第3个力则大小、方向均发生变化的问题.教学中应先让学生正确分析物体所受的3个力，将3个力的矢量首尾相连组成封闭的三角形.然后将方向不变的力的矢量延长，根据第3个力的变化情况画出变化后的矢量三角形，比较这些不同形状的矢量三角形，各力的大小及变化情况就很清楚了.

【例2】如图5所示，一个匀质球放在光滑斜面上，斜面倾角为α，在斜面上有一光滑的不计厚度的木板挡住球，使之处于静止状态．今使板与斜面的夹角β缓慢增大，在此过程中，挡板对球的压力F1和斜面对球的支持力F2的大小如何变化？

图5 例2题图

图6 矢量三角形法分析例2

解析:本题可以用解析法列方程根据三角函数判断，但非常复杂，计算量大，可采用矢量三角形图解法，如图6所示.

将重力mg,挡板对球的压力F1和斜面对球的支持力F2组成一个三角形，重力的大小和方向不变，斜面对球的支持力F2的方向不变，在增大β角的过程中，可以很明显地看出斜面对球的支持力随β增大而减小；挡板对球的支持力先减小后增大，而且在β=90°，即挡板与斜面垂直时，挡板对球的支持力最小.

2.3 相似三角形

如果物体所受的3个力中，一个力大小、方向不变，其他两个力的方向均发生变化，且3个力中没有二力保持垂直关系，可以利用相似三角形，找到力的矢量三角形和几何三角形相似来解决问题.先分析物体的受力，将3个力的矢量首尾相连组成一个力的三角形，再寻找与力的三角形相似的几何三角形，利用力的三角形与几何三角形相似，建立比例关系，把力的大小变化问题转化为几何三角形边长的大小变化问题进行讨论.

【例3】如图7所示，一个重为mg的小环，套在竖直放置的半径为R的光滑大圆环上．有一劲度系数为κ，自然长度为L(L<2R)的轻弹簧，其上端固定在大圆环的最高点A，下端与小环相连，不考虑一切摩擦，则小环静止时弹簧与竖直方向的夹角θ为多大？

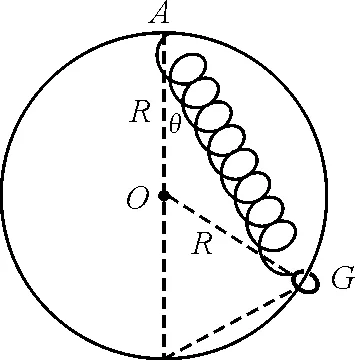
图7 例3题图

解析:将重力mg,弹簧拉力F,圆环对小环的支持力FN组成一个有关力的矢量三角形，如图8所示，根据几何知识，可以在图中找到一个几何三角形与其相似，根据相似三角形的性质，有

图8 相似三角形分析例3

可解得

所以

2.4 矢量圆法

矢量圆法，即作辅助圆，适用该方法的问题类型可分为两种，第1种情况是3个力中其中一个力大小、方向不变，另两个力方向夹角不变，第2种情况是3个力中其中一个力大小、方向不变，有一个力大小不变、方向改变.第1种情况在运用矢量圆法时，以不变的力为弦作个圆，利用同一条弦对应的圆周角相等，在辅助的圆中很容易画出两力夹角不变的力的矢量三角形，从而轻易判断各力的变化情况.2017年高考全国卷Ⅰ理综第21题就是这种情况.第2种情况应以大小不变、方向变化的力为半径作一个辅助圆，在辅助的圆中画出其中一个力大小不变、方向改变的力的矢量三角形，从而轻易判断各力的变化情况.

【例4】如图9所示，在“验证力的平行四边形定则”实验中，用A，B两只弹簧测力计把像皮条上的结点拉到某一位置O，这时两绳套AO和BO的夹角∠AOB小于90°，现保持弹簧测力计A的示数不变而改变其拉力方向使α角减小，那么要使结点仍在位置O，就应调整弹簧测力计B的拉力大小及β角，则下列调整方法中可行的是( )

A.增大B的拉力，增大β角

B. 增大B的拉力，β角不变

C.增大B的拉力，减小β角

D.B的拉力大小不变，增大β角

图9 例4题图

解析:将像皮条对结点O的拉力T，弹簧测力计A的拉力TA，弹簧测力计B的拉力TB组成三角形，在保持像皮条对结点O的拉力T不变的前提下，以弹簧测力计A的拉力TA为半径画矢量圆，改变其方向使α角减小，做出矢量三角形，如图10所示，从图形上可以直接得出结论.

图10 矢量图法分析例4

2.5 多力动态平衡转化为三力动态平衡

很多物体的平衡不仅仅局限于三力的汇交情形，涉及到多个力的平衡，往往这些问题的解决需要引入摩擦角等，将力的平衡问题转化为三力动态平衡的几何问题进行处理.

【例5】一质量为m的物体置于倾角为α的斜面上，物体与斜面间的动摩擦因数为μ，若要使物体沿斜面向上匀速滑行，求拉力的最小值.

解析:教学中对本题常用的处理方法是根据平衡条件，假设拉力与斜面的夹角为θ，利用正交分解得到函数F=F(θ)，再求极值，但运用这种方法，计算过程非常繁琐，并且要利用三角函数的推导、变换求解，对数学知识的要求很高.我们可以换一种教学思路.引入全反力，化四力平衡为三力平衡，根据矢量三角形求解.用全反力R代替支持力和摩擦力，则

物体只受到重力mg,拉力F,全反力R，如图11所示，摩擦角φ=arctanμ，由矢量三角形和三力动态平衡可知,当F垂直于全反力时，拉力F最小，此时最小值为

图11 多力动态平衡转化为三力动态平衡

可以看出，引入摩擦角的好处就是通过全反力的等效替代，减少力的个数，化多力平衡为三力平衡，通过矢量三角形迅速确定临界平衡状态，把平衡问题的判断转化为寻求角度之间的关系，这是求解多力平衡的重要思想方法.

3 结束语

在教学过程中，通过对上述高考题的分析，引导学生充分利用解析法、矢量三角形图解法、相似三角形、矢量圆、拉密定理或正弦定理解决动态平衡问题，结合动画展示动态变化过程，可有效提高学生利用数学工具处理物理问题的能力，促进发散性科学思维的培养，有效提高学生的核心能力和创新思维能力，落实核心素养.