从泡利矩阵解析量子力学中的几类典型计算问题*

王丽华

(山西大同大学物理与电子科学学院 山西 大同 037009)

量子力学不仅是物理学中的重要基础理论之一，而且在材料学、化学、宇宙学和生物学等有关学科和众多近代技术中也得到了广泛应用[1]. 本文利用泡利矩阵解析了量子力学中的几类典型计算问题，较好地理解和诠释了量子力学中的一些基本概念和原理.

1 求算符的本征值和所属的本征函数

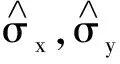
解析：设

其本征值为λ，本征函数为

即

移项得

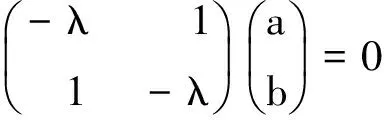
上式是一个线性齐次代数方程组，它有非零解的条件是系数行列式等于零，即

解得

λ=±1

把λ=1代入本征值方程

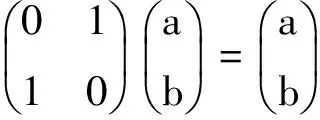
解得

a=b

即

利用波函数的归一化条件

得到

即

把λ=-1代入本征值方程

解得

-a=b

即

利用波函数的归一化条件

得到

即

同理可得

其本征值为±1，对应的本征函数为

设

其本征值为±1，对应的本征函数为

求解算符的本征值和所属的本征函数问题的一般步骤为：

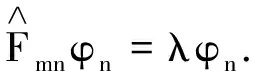
(2)将等号右边部分移至左边，得到一个线性齐次代数方程组

式中克罗内克δ符号(Kronecker delta symbol)δmn具有下面的性质：

(3)这个线性齐次代数方程组有非零解的条件是系数行列式等于零，即

detFmn-λδmn=0

上式称为久期方程. 求解久期方程可以得到一组λ值：λ1,λ2,…,λn,…,它们就是F的本征值. 把求得的λi分别代入线性齐次代数方程组就可以求得与这λi对应的本征矢φi(i=1,2,…,n,…).

2 求算符的对角化矩阵及使其对角化的么正变换矩阵

解析：对角化的矩阵为

对应的本征函数为

由上题可知，在σz表象

对应的本征函数为

其中

故

本题体现了量子力学中的一个重要结论：算符在其自身表象是一个对角矩阵，对角元素为其本征值，且算符的表象变换不改变它的本征值.

求解算符的对角化矩阵及使其对角化的么正变换矩阵的一般步骤为：

(1)将算符的本征值λii=1,2,…依次排列为矩阵的对角元素，其他非对角元素全部为零；

(2)将算符的本征值λi对应的本征矢量φ1,φ2,…,φn并列就可得到么正变换矩阵S.

3 算符和波函数的表象变换

试在σx表象中，求σz的本征态.

解析：在σz表象

σx的本征值与本征态为

将φ1，φ2并列得到由σz表象到σx表象的么正变换矩阵

在σx表象，σz的矩阵为

λ=1

λ=-1

本题运用了量子力学中力学量和态的表象变换公式

F′=S-1FS=S+FS

b=S-1a=S+a

满足S-1=S+的矩阵称为么正矩阵，由么正矩阵所表示的变换称为么正变换. 所以由一个表象到另一个表象的变换是么正变换.

解这类型题直接代公式就可以.

4 求力学量的期望值及可能取值的概率

(2) 求t>0时，电子自旋沿负y方向的概率[2, 3].

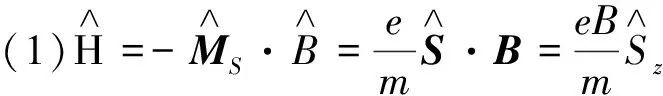
方程的解为

因此任意t时刻的波函数为

由

得到

令

ψt=a1ψ++a2ψ-

其中

t>0时，电子自旋沿负y方向的概率为

式中cn与x无关，本征函数φnx的这种性质称为完全性.cn可以由ψx和φnx求得

即

假设任一函数ψx已归一化，可得

另外，本题还用到了力学量期望值的计算公式

解这类型题只需直接代公式.

1 周世勋. 量子力学教程.北京：高等教育出版社, 2016. 174 ～ 177

2 陈鄂生. 量子力学习题与解答.北京：科学出版社, 2012. 401 ～ 404

3 史守华，谢传梅. 量子力学考研辅导.北京：清华大学出版社, 2015. 13 ～ 20