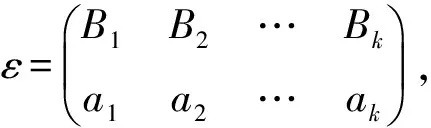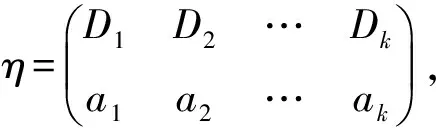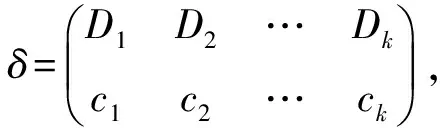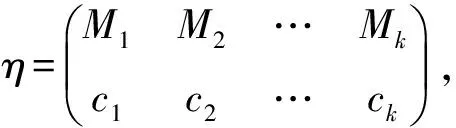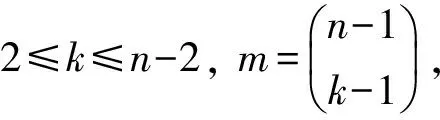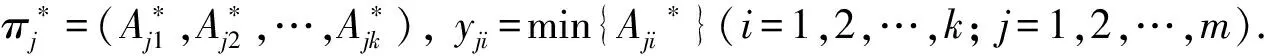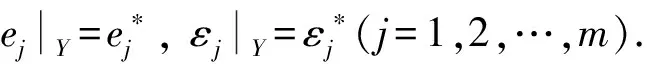半群Q(k)的极大正则子半带
2018-03-27阮海灯游泰杰
阮海灯, 游泰杰, 赵 平
(贵州师范大学 数学科学学院, 贵阳 550001)
1 引言与预备知识
设S是半群且a∈S, 若a2=a, 则称a是幂等元; 若存在b∈S, 使得a=aba, 则称a是正则元; 若半群S的每个元均为正则元, 则称半群S是正则半群. 设A是半群S的非空子集, 若S中的每个元都可以表示成A中有限个元的乘积, 则称A是S的生成集, 记作S=〈A〉. 若S由幂等元生成, 则称S为一个半带. 若半带S是正则半群, 则称S为正则半带. 设S是正则半带(正则半群),T是S的正则子半带(正则子半群)(T⊂S), 且满足: 对S的任意正则子半带(正则子半群)U, 有T⊂U⟹U=S, 则称T为S的极大正则子半带(极大正则子半群).
设T(X)和O(X)分别是X上的全变换半群和保序全变换半群,Y是X的非空子集, 令
T(X,Y)={α∈T(X):Xα⊆Y}, F(X,Y)={α∈T(X,Y):Xα⊆Yα}, OF(X,Y)=O(X)∩F(X,Y),
则OF(X,Y)均为T(X),O(X),F(X,Y)的子半群. 文献[1]研究了半群T(X,Y)的自同构; 文献[2]证明了F(X,Y)是T(X,Y)的最大正则子半群, 并确定了T(X,Y)中的Green关系; 文献[3]研究了F(X,Y)的Green关系, 并得到了F(X,Y)的极大正则子半群的完全分类; 文献[4]得到了当X为有限集时, F(X,Y)的秩与F(X,Y)的每个真理想Q(F,k)的秩及幂等元秩; 文献[5]确定了OF(X,Y)的Green关系, 并证明了当Y为有限集时, OF(X,Y)是由幂等元生成的正则半群; 文献[6-7]分别研究了当X为有限集时, 半群O(X)的理想, 分别得到了其极大子半群和极大正则子半带的完全分类. 根据文献[5], 当Y为有限集时, OF(X,Y)的Green关系有如下刻画: 对任意α,β∈OF(X,Y), 有
αLβ⟺Im(α)=Im(β),αRβ⟺Ker(α)=Ker(β),αJβ⟺|Im(α)|=|Im(β)|.
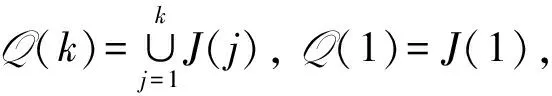
关于OF(X,Y)还有以下基本事实: OF(X,Y)的理想构成一个链, 即
Q(1)⊂Q(2)⊂…⊂Q(n-1)⊂Q(n)=OF(X,Y).

引理1[8]设x,y是完全0-单半群中的两个非零元, 则xy≠0当且仅当Lx∩Ry中含有幂等元. 此时xy∈Ly∩Rx.
引理2[8]设S是一个完全0-单半群,x,y是完全0-单半群中两个非零元, 则:
2 主要结果
对任意α∈OF(X,Y), 易证α有如下表示法(称为α的标准表示):
其中: {a1,a2,…,ak}⊆Y,a1 引理3设1≤k≤n-1, 则E(J(k))⊆E(J(k+1))2. 情形1) 若i=j, 则ai,a,b∈Ai. 不妨设ai 显然η1,η2∈E(J(k+1)), 且ε=η1η2∈E(J(k+1))2. 情形2) 若i 显然ε1,ε2∈E(J(k+1)), 且ε=ε1ε2∈E(J(k+1))2. 再由ε的任意性, 可得E(J(k))⊆E(J(k+1))2. 证毕. 由引理3与文献[5]的定理可得如下推论: 推论1设1≤k≤n-1, 则Q(k)=〈E(J(k))〉. 引理4设2≤k≤n-1,α∈J(k), 则|E(Rα)|≥2且|E(Lα)|≥1. 显然ε,η∈E(Rα), 因此|E(Rα)|≥2. 设C1={x∈X:x≤a1},C2={x∈X:a1 引理5设2≤k≤n-1,α∈J(k), 则存在α1,α2∈V(α)∩J(k), 使得(α1,α2)∉L. 证明: 由引理4可知, |E(Rα)|≥2, |E(Lα)|≥1. 任取ε1,ε2∈E(Rα),η∈E(Lα),ε1≠ε2, 则(ε1,ε2)∉L(否则,ε1,ε2∈Hα与每个H-类至多有一个幂等元矛盾). 由εiRαLη(i=1,2)及Miller-Clifford定理可知,Lε1∩Rη和Lε2∩Rη包含α的逆元, 不妨分别设为α1和α2, 于是αiLεi(i=1,2), 从而(α1,α2)∉L. 此外, 由αiLεiRα可知,αiJα, 于是|Im(αi)|=|Im(α)|=k, 从而αi∈J(k). 证毕. 引理6设2≤k≤n-1,α∈J(k), 则A(α)=Q(k-1)∪(J(k)Lα)是Q(k)的极大正则子半群. 证明: 由Q(k-1)是Q(k)的理想知, 要证A(α)是半群, 只需证对任意β,γ∈J(k)Lα, 有βγ∈A(α). 显然βγ∈Q(k-1)或βγ∈J(k). 若βγ∈J(k), 则Im(βγ)=Im(γ),γ∉Lα, 于是βγ∈J(k)Lα. 因此A(α)是Q(k)的子半群. 显然Q(k-1)是正则的. 对任意β∈J(k)Lα, 由引理5可知, 存在β1,β2∈V(β)∩J(k), 使得(β1,β2)∉L, 于是β1,β2中必有一个属于J(k)Lα, 即J(k)Lα中必存在β的逆元, 从而β是正则的. 进而A(α)是正则半群. 假设S是Q(k)的正则子半群, 使得A(α)⊂S. 任取β∈SA(α), 则β∈Lα. 由引理4知, |E(Rβ)|≥2, 不妨设ε,η∈E(Rβ)且ε≠η, 则ε,η中必有一个不属于Lα(否则,ε,η∈Hα, 与每个H-类至多有一个幂等元矛盾). 不妨设ε∉Lα, 于是Lε⊆J(k)Lα⊆A(α)⊂S, 从而由引理2可得,Lα=Lβ=Lεβ⊂S. 进而S=Q(k), 因此A(α)是Q(k)的极大正则子半群. 证毕. 设2≤k≤n-1,α∈J(k). 用Mid(α),Minker(α),Maxker(α)分别表示Im(α)(min{Im(α)},max{Im(α)}),(min{Im(α)})α-1,(max{Im(α)})α-1之集. 令 注意到当k=2时,N1(k)=Ø, 因此N(k)=N2(k)∪N3(k). 引理7设2≤k≤n-1,α∈N(k), 则存在ε∈E(Lα), 使得ε∉Rα. 引理8设2≤k≤n-1,α∉N(k), 则存在ε∈E(Rα), 使得|E(Lε)|=1. 引理9设2≤k≤n-1,α∈N(k),β∈J(k)Rα, 则存在γ∈J(k)Rα, 使得β=βγβ. 1) 若γ∉Rα, 则结论显然. 2) 若γ∈Rα, 则Ker(α)=Ker(γ), 于是Ai=Ci(i=1,2,…,k). 由α∈N(k)知,α∈N1(k)或α∈N2(k)或α∈N3(k). 引理10设2≤k≤n-1,α∈N(k), 则B(α)=Q(k-1)∪(J(k)Rα)是Q(k)的极大正则子半群. 证明: 由Q(k-1)是Q(k)的理想知, 要证B(α)是半群, 只需证对任意β,γ∈J(k)Rα, 有βγ∈B(α). 显然βγ∈Q(k-1)或βγ∈J(k). 若βγ∈J(k), 则Ker(βγ)=Im(β),β∉Rα, 于是βγ∈J(k)Rα. 因此B(α)是Q(k)的子半群. 由引理9及Q(k-1)是正则的可知, B(α)是Q(k)的正则子半群. 假设S是Q(k)的正则子半群, 使得B(α)⊂S. 任取β∈SB(α), 则β∈Rα. 由引理7知, 存在ε∈E(Lβ),ε∉Rβ=Rα. 于是Rε⊆J(k)Rα⊆B(α)⊂S, 从而由引理2, 可得Rα=Rβ=βRε⊂S. 进而S=Q(k), 因此B(α)是Q(k)的极大正则子半群. 证毕. 本文主要结果如下: 定理1设2≤k≤n-1, 则半群Q(k)的极大正则子半群有且仅有下列两类: 1) A(α)=Q(k-1)∪(J(k)Lα),α∈J(k); 2) B(β)=Q(k-1)∪(J(k)Rβ),β∈N(k). 证明: 由引理6和引理10可知, A(α),B(β)是Q(k)的极大正则子半群. 假设T是Q(k)的极大正则子半群, 但不是引理9中的形式. 由Q(k)=〈E(J(k))〉, Q(k-1)是正则的可知,T∪Q(k-1)是Q(k)的真正则子半群, 从而Q(k-1)⊆T, 因此对任意α∈J(k),β∈N(k), 有T∩Lα≠Ø且T∩Rβ≠Ø. 否则, 存在α∈J(k), 使得T∩Lα=Ø或存在β∈N(k), 使得T∩Rα=Ø, 于是Lα⊆J(k)T或Rβ⊆J(k)T, 从而T⊆A(α)⊂Q(k)或T⊆B(α)⊂Q(k), 由T是Q(k)的极大子半群可得,T=A(α)或T=B(β), 矛盾. 下面证明E(J(k))⊆E(T). 假设E(J(k))E(T)≠Ø. 任取ε∈E(J(k))E(T)⊆J(k). 由T∩Lε≠Ø知,T是正则的, 因此E(T)∩Lη≠Ø. 若ε∈N(k), 则T∩Rε≠Ø, 再由T是正则的可知,E(T)∩Rε≠Ø. 若ε∉N(k), 由引理8知, 存在η∈E(Rε)使得|E(Lη)|=1. 由T∩Lη≠Ø及T是正则的可知,E(T)∩Lη≠Ø. 从而η∈E(T), 因此E(T)∩Rε≠Ø. 取ξ∈E(T)∩E(Lε),γ∈E(T)∩E(Rε), 于是由引理1, 可得ξγ∈Rξ∩Lγ∩T. 再由Miller-Clifford定理, 可得存在δ∈V(ξγ)∩T, 使得δ∈Lξ∩Rγ=Rε∩Lε=Hε, 则δ是群Hε中的元, 于是ε=δm∈T, 与ε∈E(J(k))E(T)矛盾, 从而E(J(k))⊆E(T)⊆T, 进而由推论1, 可得Q(k)=〈E(J(k))〉⊆〈T〉=T. 因此T=Q(k)与T是Q(k)的极大正则子半群矛盾. 证毕. 设π={A1,A2,…,Ak}是X上的一个划分,A是X的子集且|A|=k. 对任意i, 若Ai中有一个元素属于A, 则称π是A的一个横截, 记为π#A(或A#π). 引理12设2≤k≤n-2,α∉N(k), 则α∈Rπ, 从而存在j∈{1,2,…,m}, 使得Rα=Rπj. 引理13设2≤k≤n-2,α∉LA, 则存在η∈E(Rπ)∩Lα. 引理14设2≤k≤n-2,α∉Rπ, 则存在η1,η2∈E(LARπ)∩Rα, 使得η1≠η2. 引理15设2≤k≤n-2,α∈J(k), 则J(k)Lα⊆〈E(J(k)Lα)〉. 证明: 任取β∈J(k)Lα. 下面分两种情形讨论. 情形1)Lα∉LA. ① 若β∈Rπ,β∈LA, 则存在j,t∈{1,2,…,m}, 使得β∈Rπj∩LAt. 若j=t, 则β=ej; 若j ② 若β∈Rπ,β∉LA, 则由引理13知, 存在η∈E(Rπ)∩Lβ, 不妨设η∈Rπj. 由e∈Rπj∩LAj, 可得β=γη, 其中γ∈Rβ∩LAj, 再由情形1)中①知,γ∈〈E(J(k)Lα)〉, 因此β∈〈E(J(k)Lα)〉. ③ 若β∉Rπ, 则由引理14知存在η∈E(LARπ)∩Rα, 不妨设η∈LAj, 于是η∈Rβ∩LAj, 从而β=ηγ, 其中γ∈Lβ∩Rej, 再由情形1)中①,②可知γ∈〈E(J(k)Lα)〉, 因此β∈〈E(J(k)Lα)〉. 情形2)Lα∈LA, 不妨设Lα=LAr. ① 若β∈Rπ,β∈LA, 则存在j,t∈{1,2,…,m}, 使得β∈Rπj∩LAt. 若j≤t ② 若β∈Rπ,β∉LA, 则由引理13知, 存在η∈E(Rπ)∩Lβ, 不妨设η∈Rπj. 由|E(Rπj)∩LA|≥2知, 存在γ∈LAj∩Rβ或γ∈LAj+1∩Rβ, 使得β=γη且γ∉LAr. 再由情形2)中①知,γ∈〈E(J(k)Lα)〉, 因此β∈〈E(J(k)Lα)〉. ③ 若β∉Rπ, 则由引理14知, 存在η1,η2∈E(LARπ)∩Rα, 使得η1≠η2, {η1,η2}中必存在一个不属于LAr. 不妨设η1∉LAr,η1∈LAj, 于是η1∈Rβ∩LAj, 从而β=η1γ, 其中γ∈Lβ∩Rej, 再由情形2)中①,②可知γ∈〈E(J(k)Lα)〉, 因此β∈〈E(J(k)Lα)〉. 最后由β的任意性可得J(k)Lα⊆〈E(J(k)Lα)〉. 证毕. 设E1={∈E(J(k)): |E(L)|=1},L1=∪{L:∈E1}. 由引理8可知, 若∈E1, 则∈Rα,α∉N(k). 显然L1⊆J(k)LA. 引理16设2≤k≤n-2,α∈N(k), 则J(k)Rα⊆〈E(J(k)Rα)〉. 证明: 任取β∈J(k)Rα. 由α∈N(k)及引理12, 可分以下两种情形讨论. 情形1)Rα∉Rπ. ① 若β∈Rπ,β∈LA, 则类似引理15情形1)中①, 可得β∈〈E(J(k)Rα)〉. ② 若β∈Rπ,β∉LA, 则由引理13知, 存在η∈E(Rπ)∩Lβ, 不妨设η∈Rπj. 由e∈Rπj∩LAj知,β=γη, 其中γ∈Rβ∩LAj, 再由情形1)中①知,γ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. ③ 若β∉Rπ, 则由引理14知, 存在η∈E(LARπ)∩Rα, 不妨设η∈LAj, 于是η∈Rβ∩LAj, 从而β=ηγ, 其中γ∈Lβ∩Rej, 再由情形1)中①,②可知γ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. 情形2)Rα∈Rπ, 不妨设Rα=Rπr. ① 若β∈Rπ,β∈LA, 则存在j,t∈{1,2,…,m}, 使得β∈Rπj∩LAt. 若j≤t ② 若β∈Rπ,β∉LA, 则: (i) 若β∈L1, 则存在η∈Lβ∩E1, 使得η∉Rα. 由引理12知η∈Rπ, 不妨设η∈Rπj, 从而存在γ∈Lej∩Rβ, 使得β=γη. 由情形2)中①可知γ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. (ii) 若β∉L1, 则|E(Lβ)|≥2, 从而存在η1,η2∈E(Lβ), 使得η1≠η2. {η1,η2}中必有一个不属于Rα, 不妨设η1∉Rα. 若η1∈Rπ, 则η1∈Rπt, 从而存在θ∈Let∩Rβ, 使得β=θη. 由情形2)中①可知θ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. 若η1∉Rπ, 则η1∈Rρ,ρ∉Rπ. 再由引理14知, 存在σ∈E(LARπ)∩Rρ, 从而存在ζ∉Rα,ζ∈Rβ∩Lσ, 使得β=ζη1. 由情形2)中①可知ζ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. ③ 若β∉Rπ, 则由引理14知, 存在η∈E(LARπ)∩Rβ, 不妨设η∈LAj, 从而存在γ∈Lβ∩Rej(否则,γ∈Lβ∩Rεj-1), 使得若ej∉Rα, 则β=ηγ. 由情形2)中①,②可知γ∈〈E(J(k)Rα)〉, 因此β∈〈E(J(k)Rα)〉. 最后由β的任意性可得J(k)Rα⊆〈E(J(k)Rα)〉. 证毕. 定理2设2≤k≤n-2, 则半群Q(k)的极大正则子半带有且仅有下列两类: 1) A(α)=Q(k-1)∪(J(k)Lα),α∈J(k); 2) B(β)=Q(k-1)∪(J(k)Rβ),β∈N(k). 证明: 由引理6、 引理10、 引理15、 引理16可知, A(α),B(β)是Q(k)的极大正则子半带. 类似定理1的证明可得结论, 证毕. [1] Symons J S V. Some Results Concerning a Transformation Semigroup [J]. J Aust Math Soc, 1975, 19(4): 413-425. [2] Sanwong J, Sommanee W. Regularity and Green’s Relations on a Semigroup of Tranformations with Restricted Range [J/OL]. Int J Math Math Sci, 2008-09-18. doi: 10.1155/2008/794013. [3] Sanwong J. The Regular Part of a Semigroup of Transformations with Restricted Range [J]. Semigroup Forum, 2011, 83(1): 134-146. [4] Sommanee W, Sanwong J. Rank and Idempotent Rank of Finite Full Transformation Semigroups with Restricted Range [J]. Semigroup Forum, 2013, 87(1): 230-242. [5] Sommanee W, Sanwong J. Order-Preserving Transformations with Restricted Range: Regularity, Green’s Relations, and Ideals [J].Algebra Universalis, 2015, 74(3/4): 277-291. [6] Dimitrova I, Koppitz J. On the Maximal Subsemigroups of Some Transformation Semigroups [J]. Asian-European J Math, 2008, 1(2): 189-202. [7] ZHAO Ping. Maximal Regular Subsemibands of Finite Order-Preserving Transformation SemigroupsK(n,r) [J]. Semigroup Forum, 2012, 84(1): 97-115. [8] Howie J M. Fundamentals of Semigroup Theory [M]. Oxford: Oxford Press, 1995. [9] Garba G U. On the Idempotent Ranks of Certain Semigroups of Order-Preserving Transformations [J]. Portugal Math, 1994, 51(2): 185-204.