基于三维自治系统复杂网络的混沌保密通信系统

付宏睿, 董永刚, 张建刚

(1. 安阳学院 建筑工程学院, 河南 安阳 455000; 2. 兰州交通大学 数理学院, 兰州 730070)

目前, 基于复杂网络的混沌同步问题已引起人们广泛关注[1-2]. 文献[3]通过设计控制器, 对基于自适应的非线性耦合网络进行了有限时间同步控制； 文献[4]研究了复杂网络在脉冲信号下的网络同步问题; 文献[5]基于Lorenz系统, 研究了小世界网络各变量间替换耦合的同步问题； 文献[6]基于投影同步, 研究了复杂网络混沌系统的有限时间同步. 但对复杂网络同步应用的研究文献报道较少. 本文将一个三维自治系统与复杂网络相结合, 利用该系统的混沌同步将其应用于保密通信[7-12]中. 在信息传输中加入Gauss白噪声[13-14]对混沌保密通信系统进行干扰, 并用小波变换[15]原理对信号进行去噪处理, 由MATLAB数值仿真结果可见, 该系统可无失真地恢复有用信号.

1 数学模型

选取一个三维自治混沌系统, 该系统的状态方程为

(1)

其中:X=(x1,x2,x3)T∈3为系统的状态变量;a,b,c∈为系统参数. 该系统用矩阵表示为其中:

由矩阵表达式可知, 该系统中a11a22=0. 由于Lorenz系统为a11a22>0, Chen系统为a11a22<0, Liu系统为a11a22<0, 且该系统与上述3个经典混沌系统不具有拓扑等价性, 因此该三维自治系统是处于经典混沌系统间新的临界系统.

1.1 系统(1)的耗散性与吸引子的存在性

由于系统(1)的向量场散度为

图1 混沌吸引子的相图Fig.1 Phase diagram of chaotic attractor

1.2 系统(1)吸引子的数值仿真

当系统(1)的参数a=5,b=4,c=-4时, 由于

V=-2a-c<0.

因此其具有耗散性, 该系统存在如图1所示的混沌吸引子, 其中： (A)为三维相空间的混沌吸引子； (B)为x-y平面投影； (C)为x-z平面投影； (D)为y-z平面投影.

2 基于系统

(1)的复杂网络同步

选取由N个相同节点通过耦合构成的全局耦合网络, 其中第i个节点的n维动力系统状态方程为

(2)

将系统(1)表示为网络的各节点, 若取节点数N=3, 则由该系统组成3个节点的全局耦合网络模型为

(3)

(4)

(5)

根据系统(3)～(5)节点组成的网络模型, 通过MATLAB进行数值仿真, 可得如图2所示的同步误差结果, 其中： (A)为节点1和2的同步误差; (B)为节点2和3的同步误差； (C)为节点1和3的同步误差. 由图2可见, 各系统的初始参数不同, 但通过控制后, 各节点间均能较快达到同步.

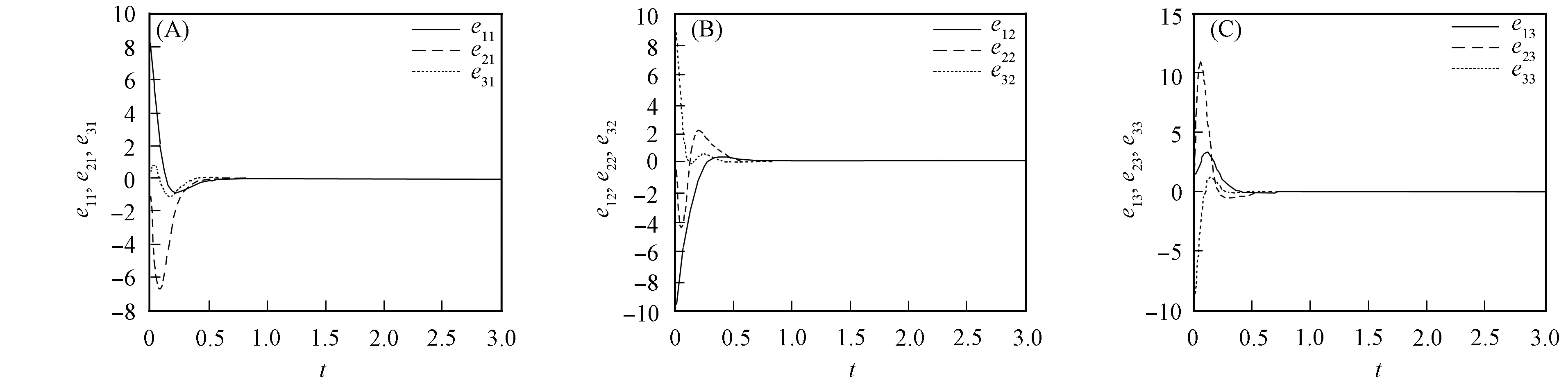
图2 耦合网络同步误差Fig.2 Synchronization error of coupling network

3 基于耦合网络同步的混沌保密通信

3.1 保密通信原理

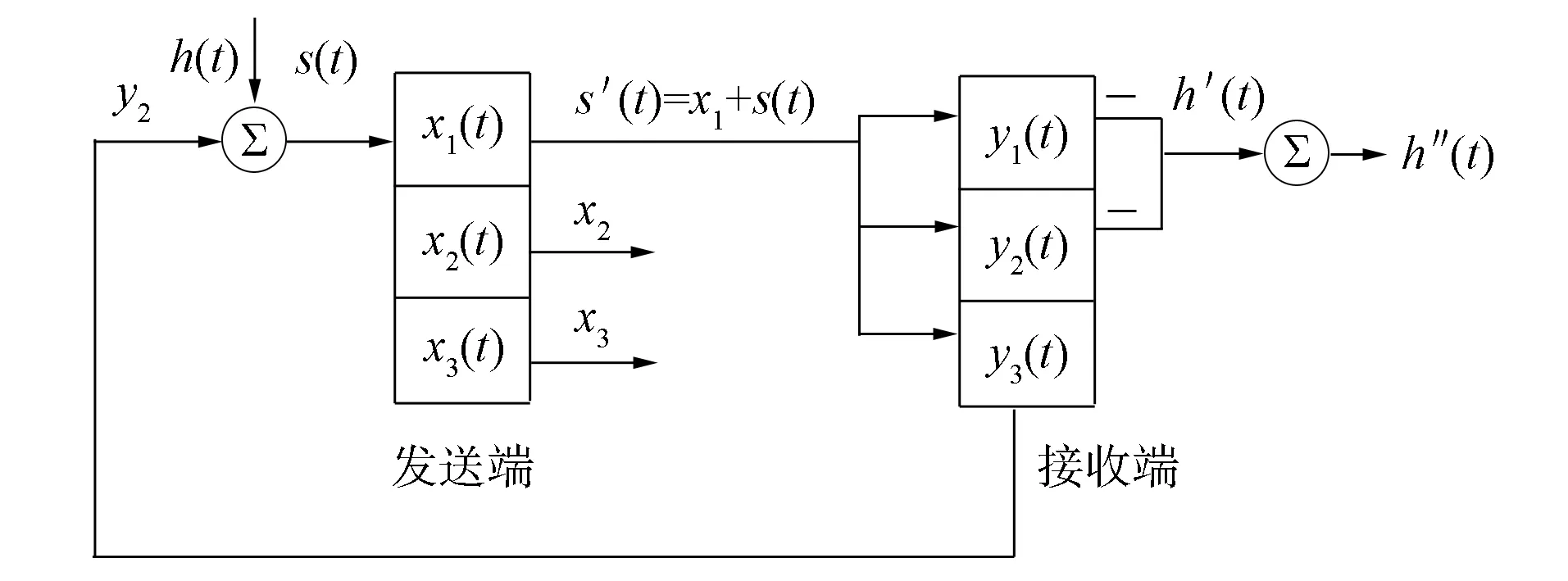
图3 保密通信系统原理Fig.3 Principle of secure communication system

基于三维自治系统的全局耦合网络模型的同步, 提出一种复杂网络的混沌保密通信系统, 如图3所示. 先在发送端将信息经两次加密后, 再在接收端经两次解密后恢复信息. 由于该三维自治系统线性部分系数矩阵对应的项与经典混沌系统不同, 是处于经典混沌系统间的临界系统. 因此将其应用于保密通信将极大提高信息的保密性.

3.2 基于小波去噪的保密通信数值仿真

将如图4所示的Gauss白噪声信号加入保密通信的过程中, 由于信息在传输过程中受严重干扰, 因此在解密过程中需考虑噪声的消除问题.

小波去噪原理如图5所示. 该去噪方法先将待测信号与噪声信号进行叠加, 由于混沌信号的能量谱较集中, 而噪声在小波域中的能量谱较分散, 因此含噪信号在经预处理后, 利用小波变换原理[16]对信号进行多尺度分解, 再选择适当的小波阈值进行分尺度去噪, 最后将去噪处理后的信号进行重构即可得到原有用信号.

图4 Gauss白噪声及其频谱Fig.4 Gaussian white noise and frequency spectra

图5 小波去噪原理Fig.5 Principle of wavelet de-noising

选取系统(3)为发射端, 系统(4)为接收端, 用上述保密通信方法, 将离散信号h(t)作为有用信息进行传输, 则含噪信号为

s(t)=h(t)+x22(t)+n(t),

其中n(t)为5 dB的Gauss白噪声信号.

令节点1为发射系统:

节点2为接收系统:

通过MATLAB进行数值仿真, 保密通信下离散信号的传输如图6所示, 其中： (A)为x22的时间序列; (B)为有用信息h(t); (C)和(D)分别为信道中第一次与第二次加密后的含噪信号s(t)和s′(t); (E)和(F)分别为第一次解密与第二次解密后的含噪信号h′(t)和h″(t); (G)为采用小波阈值去噪处理后的有用信号h1(t).

由图6可见, 经两次加密与两次解密后, 离散信号可被恢复, 但信号波形发生了改变, 这是由于受噪声干扰所致. 通过小波阈值去噪处理后, 离散信号可被较好地恢复.

图6 保密通信下离散信号的传输Fig.6 Transmission of discrete signals under secure communication

综上, 本文将一个三维自治系统作为网络节点, 研究了该系统复杂网络的混沌同步问题, 并设计了基于该网络同步的保密通信系统. 由于该系统的结构与动力学特性较复杂, 因此可提高保密程度, 从而增加破译难度. 为对信息传输进行干扰, 在传输过程中加入了Gauss白噪声, 经小波阈值去噪处理后, 使得有用信号可无失真地被恢复.

[1] ZHANG Rong, HU Manfeng, XU Zhenyuan. Synchronization in Complex Networks with Adaptive Coupling [J]. Physics Letters A, 2007, 368(3/4): 276-280.

[2] ZHOU Jin, LU Jun’an, LÜ Jinhu. Pinning Adaptive Synchronization of a General Complex Dynamical Network [J]. Automatica, 2008, 44(4): 996-1003.

[3] 毛北行, 张玉霞. 具有非线性耦合复杂网络系统的有限时间混沌同步 [J]. 吉林大学学报(理学版), 2015, 53(4): 757-761. (MAO Beixing, ZHANG Yuxia. Finite-Time Chaos Synchronization of Complex Networks Systems with Nonlinear Coupling [J]. Journal of Jilin University (Science Edition), 2015, 53(4): 757-761.)

[4] 王慧, 王红飞, 牛玉俊. 一类节点结构相同的复杂网络脉冲同步 [J]. 辽宁工程技术大学学报(自然科学版), 2013, 32(1): 140-144. (WANG Hui, WANG Hongfei, NIU Yujun. Impulsive Synchronization of a Kind of Complex Networks with Same Nods[J]. Journal of Liaoning Technical University (Natural Science), 2013, 32(1): 140-144.)

[5] 张冬梅, 马丽红, 张旭, 等. 复杂动力网络的单变量替换互耦合同步 [J]. 河北工业大学学报, 2010, 39(3): 65-68. (ZHANG Dongmei, MA Lihong, ZHANG Xu, et al. Synchronization of Single-Variable Substitution and Its Application in Complex Dynamic Networks [J]. Journal of Hebei University of Technology, 2010, 39(3): 65-68.)

[6] 毛北行, 李巧利. 复杂网络同步时间可控的投影同步 [J]. 安徽大学学报(自然科学版), 2015, 39(2): 13-16. (MAO Beixing, LI Qiaoli. Time-Controllable Projective Synchronization of Complex Networks [J]. Journal of Anhui University (Natural Science Edition), 2015, 39(2): 13-16.)

[7] LIU Chongxin, LIU Tao, LIU Ling, et al. A New Chaotic Attractor [J]. Chaos Solitons and Fractals, 2004, 22(5): 1031-1038.

[8] 仓诗建, 陈增强, 袁著祉. 一个新四维非自治超混沌系统的分析与电路实现 [J]. 物理学报, 2008, 57(3): 1493-1501. (CANG Shijian, CHEN Zengqiang, YUAN Zhuzhi. Analysis and Circuit Implementation of a New Four-Dimensional Non-autonomous Hyper-Chaotic System [J]. Acta Physica Sinica, 2008, 57(3): 1493-1501.)

[9] 韩新风, 高智中, 章毛连. 一个新的自治混沌系统及其电路实现 [J]. 武汉大学学报(理学版), 2011, 57(3): 196-200. (HAN Xinfeng, GAO Zhizhong, ZHANG Maolian. A New Autonomous Chaotic System and Its Circuit Realization [J]. Journal of Wuhan University (Natural Science Edition), 2011, 57(3): 196-200.)

[10] 赵建峰, 王淑英, 李险峰, 等. 基于分数阶超混沌的新图像加密算法 [J]. 四川大学学报(自然科学版), 2014, 51(5): 958-964. (ZHAO Jianfeng, WANG Shuying, LI Xianfeng, et al. New Algorithm for Image Encryption Based on Fractional Order Chaotic System [J]. Journal of Sichuan University (Natural Science Edition), 2014, 51(5): 958-964.)

[11] 龚美静, 瞿少成, 王晓燕. 一种通过异结构同步实现混沌保密通信新方法 [J]. 电子与信息学报, 2009, 31(6): 1442-1444. (GONG Meijing, QU Shaocheng, WANG Xiaoyan. A Novel Method of Realizing Chaotic Secure Communication by Synchronization of Different Structure [J]. Journal of Electronics & Information Technology, 2009, 31(6): 1442-1444.)

[12] Kiani B A, Fallahi K, Pariz N, et al. A Chaotic Secure Communication Scheme Using Fractional Chaotic Systems Based on an Extended Fractional Kalman Filter [J]. Commun Nonlinear Sci Num Sim, 2009, 14(3): 863-879.

[13] 杨留猛, 俞建宁, 安新磊, 等. 基于一个混沌系统的保密通信及其电路实现的研究 [J]. 四川大学学报(自然科学版), 2014, 51(3): 499-506. (YANG Liumeng, YU Jianning, AN Xinlei, et al. Study on Secure Communication and Circuit Implementation for a Chaotic System [J]. Journal of Sichuan University (Natural Science Edition), 2014, 51(3): 499-506.)

[14] 郝建红, 孙志华, 许海波. 干扰信号对两种混沌加密系统的影响及分析 [J]. 物理学报, 2007, 56(12): 6857-6864. (HAO Jianhong, SUN Zhihua, XU Haibo. Analyzing the Noise Resistance Effect for Two Chaos Secure Systems [J]. Acta Physica Sinica, 2007, 56(12): 6857-6864.)

[15] 吕顺, 何小海, 杨龙, 等. 基于小波变换系数去冗余的图像无损压缩方法 [J]. 四川大学学报(自然科学版), 2015, 52(1): 85-92. (LÜ Shun, HE Xiaohai, YANG Long, et al. An Algorithm of Lossless Image Compression Based on Wavelet Transform Coefficients to Eliminate Redundancy [J]. Journal of Sichuan University (Natural Science Edition), 2015, 52(1): 85-92.)

[16] 段清, 李凤祥, 田兆垒. 一种改进的小波阈值信号去噪方法 [J]. 计算机仿真, 2009, 26(4): 348-351. (DUAN Qing, LI Fengxiang, TIAN Zhaolei. An Improved Method for Wavelet Thresholding Signal Denoising [J]. Computer Simulation, 2009, 26(4): 348-351.)